管幕-结构法构件抗弯特性研究
2021-05-17韩现民肖明清胡大伟
韩现民,梁 显,肖明清,胡大伟
(1.石家庄铁道大学土木工程学院,石家庄 050043; 2.省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043; 3.中铁第四勘察设计院集团有限公司,武汉 430063)
1 概述
管幕-结构法是在前期顶进完成的、按照一定空间位置排列的钢管基础上,经过钢管切割、管间土体开挖、钢板焊接、钢管柱支撑等工序将相邻钢管进行连接,形成一个环向、纵向完全联通的空间,通过在其中编制钢筋、浇筑混凝土,最终形成一个大刚度的支护结构体系,其主要由钢管(管幕)、相邻钢管间连接钢板、钢板间支撑和钢筋混凝土等组成。它是在传统管幕工法的基础上,对工法的施工步序和连接方式进行优化,提出的一种新型结构,主要应用于修建地铁站、下穿既有隧道、道路、铁路等的地下结构支护体系[1-7]。管幕-结构法是利用翼缘板以及高强螺栓将相邻的钢管进行连接,形成一个共同受力且具有更高的横向承载力和刚度的支护结构[8]。管幕-结构法结合了钢和混凝土优良的受力性能,翼缘板及螺栓的连接功能不仅增强了结构的整体性,提高了结构的可靠性,而且其稳定的施工工艺能够减少对既有建筑以及地层变形的影响[9-11]。
自管幕-结构法诞生以来,其在国内外工程中得到了广泛的应用,吸引了广大学者的研究热情。关永平等[12]基于6榀STS管幕简支梁的对称集中荷载抗弯试验,研究了STS管幕构件的裂缝开展模式、破坏过程及机理,并对比分析了混凝土强度、钢管间距以及管间横向连接方式对承载力的影响规律。贾鹏蛟等[13-15]提出了管幕结构的横向和纵向受力模式的计算公式,为结构后期施工提供了理论支撑,并通过有限元分析了不同参数对翼缘板连接的管幕结构抗弯性能的影响。阎石[16-17]对管幕混凝土肋梁结构体系抗弯性能和结构节点抗剪性能进行了试验研究。张超哲[18]、阎石[19]分别对槽钢和螺纹杆连接的管幕构件力学性能及影响因素进行了试验分析。
相关文献对构件破坏机理、结构横向与纵向受力模式等进行了研究,并进行了混凝土强度、管间连接方式等对结构承载能力影响分析,获得了一定的研究成果;但作为一种新型结构,在承载机理、结构连接形式及细部设计等方面仍需深入研究,认识并掌握其承载特性,对指导与优化结构设计有着重要意义。
由于管幕结构结合了钢与混凝土两种材料,且一般情况下两种材料间不设置连接而依靠材料表面的初始粘结和摩擦,因此在受力过程中,两种材料的相互滑移(错动)是不可避免的[20]。两种材料的连接状态直接影响结构承载机理和承载能力,故进行材料界面状态对管幕-结构构件承载特性影响研究有着重要的理论价值。
以太原市下穿火车站的管幕工程为基本研究对象,基于一般力学方法和平截面假设,考虑钢管与混凝土界面完全连接和自由滑移2种极限状态下,进行了管幕构件截面抗弯承载力的计算,并分析了界面间存在粘结力作用时的截面抗弯承载力;在此基础上讨论了管壁厚度对截面抗弯承载力的影响;并对简化的下穿管幕工程用ANSYS软件建模并进行有限元分析,分析该结构的静力特性。
2 依托工程设计概况
太原火车站下穿工程地下通道设计为两孔单向四车道,采用管幕-结构法施工,其中南通道管幕段长105 m,北通道管幕段长102.5 m,最小埋深约3 m。管幕结构全宽18.2 m,全高10.5 m,每条通道设置20根φ2 m@20 mm钢管,如图1所示;钢管净间距165~265 mm,钢管之间连接细部如图2、图3所示。相邻钢管通过间隔切割、管间土体开挖、钢板(20 mm厚)焊接、板间支撑柱(外径121 mm、壁厚6.5 mm的钢管内部充填C25微膨胀细石混凝土)施做等主要工序完成环向与纵向连接,形成一个贯通空间;通过在空间内进行C40钢筋混凝土施工,最后形成钢管+钢筋混凝土支护体系。

图1 管幕结构横断面(单位:mm)

图2 钢管间环向连接细部(单位:mm)
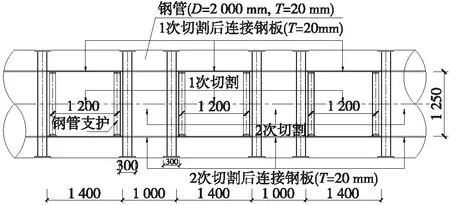
图3 钢管间纵向连接细部(单位:mm)
3 不同界面连接状态构件抗弯承载力计算原理
3.1 截面选取与简化
管幕结构主要受覆土重力、上部人群以及轨面荷载作用,选择A4、A10典型截面为分析对象,分别计算截面在不同受力阶段的抗弯承载力。
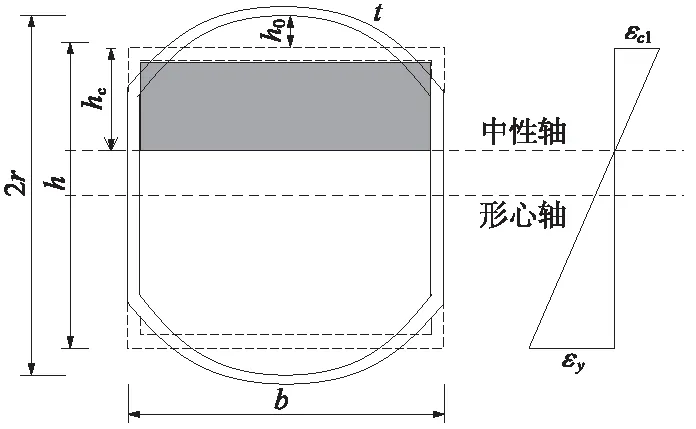
以A4截面为例,将截面划分为a、b、c三部分,如图4(a)所示。在结构施工过程中,由于孔洞内空气无法完全排出以及混凝土收缩的影响,为安全考虑,忽略a部分顶部混凝土的作用,根据承受荷载的钢面积相等的原则,将a部分等效为一个矩形。图4(a)中的c部分同样存在空气无法完全排出、混凝土收缩等问题,同时,荷载作用下底部混凝土易受拉开裂而导致混凝土失效。因此,c部分可根据以上原则等效为与a部分相同的矩形。等效后的截面如图4(b)所示,图中r为钢管的半径,h为等效后截面高度,b为截面宽度,h0为等效过程中被忽略混凝土作用的高度,可根据式(1)计算。

(1)
式中,d为连接钢板的高度;φ为钢管顶底部对应的圆心弧度;R为钢管半径;t为钢管壁厚。

图4 A4截面
3.2 抗弯承载力计算
选择钢-混凝土完全连接与自由滑移两种极限状态,对其截面抗弯承载能力进行计算[21],以对比其受力性能的差异。
参考典型的钢筋混凝土受弯梁开裂和变形过程[22],可将截面为图4(b)的钢管混凝土构件从开始受弯直至破坏分为3个受力阶段。各阶段的特征如下。
(1)混凝土开裂前阶段(M≤Mcr)
结构刚开始受力时弯矩很小,混凝土与钢管均处于线弹性阶段,截面的应力与应变为线性分布,对通常为对称截面的钢管-混凝土结构而言,其中性轴与形心轴位置重合,受压区高度hc=h/2。该阶段的钢管与混凝土的应力与曲率随弯矩成比例的增大直至受拉边缘混凝土开裂,此时所对应的弯矩为开裂弯矩Mcr。
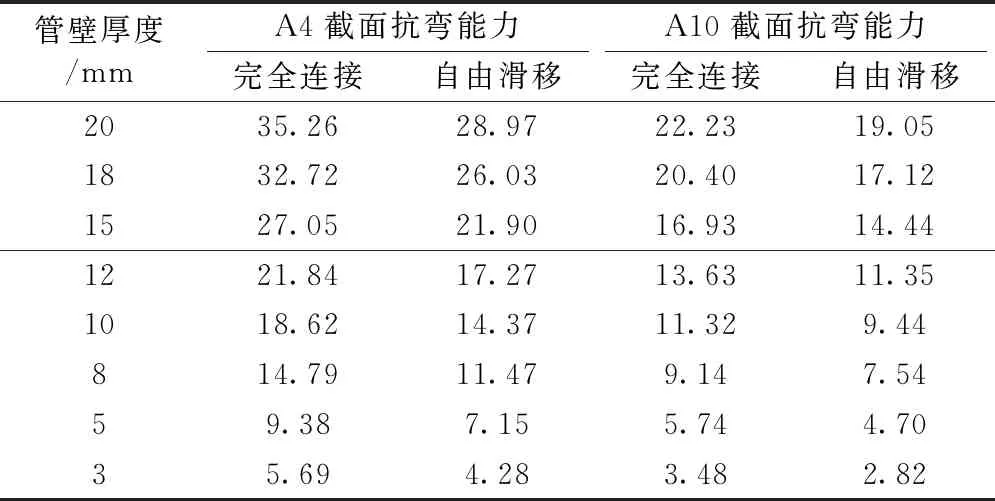
(2)近弹性工作阶段(Mcr 当弯矩超过开裂弯矩后,随弯矩的增大受拉区混凝土的开裂范围逐步向上扩展,此时裂缝截面的混凝土部分退出工作,受拉区钢管的拉应力突增(但仍处于弹性受力阶段σs 这一阶段,从混凝土开裂至钢管受拉屈服之前,弯矩增量(ΔM=My-Mcr,其中My为屈服弯矩)最大。随着弯矩的不断增大,钢管和混凝土的应力、中性轴位置和曲率等都继续稳定增大,一般结构在这一阶段使用的弯矩为(0.5~0.6)Mu,其中Mu为截面的极限抗弯承载力。 对于界面自由滑移状态的钢管-混凝土结构,在混凝土开裂后的工作阶段,钢管与核心混凝土始终围绕着各自的中性轴分别变形。核心混凝土因裂缝的发展,中性轴上移,而钢管围绕着形心轴弯曲变形,其受拉、受压边缘同时屈服。 (3)弹塑性阶段(My≤M 当钢管受拉屈服时,弯矩My≈(0.8~0.9)Mu,此时,裂缝截面受压区混凝土的应力仍小于其抗压强度fc。随着弯矩的增大,钢管受拉屈服的范围进一步扩大,同时钢管的拉应变也快速发展,从而裂缝混凝土与钢管界面的粘结会遭到破坏,混凝土沿着钢管内壁发生整体的错动。弯矩继续增大,混凝土的剩余承载力已经很小,结构几乎仅剩钢管承受弯矩,直至受拉区的钢管达到钢的极限压应变,钢管受压发生屈服。基于全塑性理论,钢管的应力不再变化而应变不断地增长直至钢管与混凝土均达到全塑性变形。 对上述三阶段的极限弯矩计算公式进行推导,基本假设如下。 ①结构从开始受力到破坏整个过程,符合平截面假定;②钢材的弹性极限强度和屈服强度均按屈服强度取值;③不考虑受拉开裂混凝土的抗拉强度;④混凝土应力-应变关系采用Rusch模型,如图5(a)所示;⑤钢的应力-应变关系采用二折线模型,如图5(b)所示。 图5 材料的应力-应变关系 图5中,σc、σt分别为混凝土的压、拉应力;fc为混凝土的轴心抗压强度;ε0为混凝土峰值压应变,εcu为混凝土极限压应变;εt0为混凝土峰值拉应变。fy为钢的屈服强度;εy为屈服应变,εy=fy/Es,Es为钢的弹性模量。 各阶段截面总抗弯承载力M可以表示为 M=Ms+Mc (2) 式中,Ms,Mc分别为钢管和混凝土承受的弯矩。 3.2.1 完全连接状态 (1)混凝土开裂前阶段 图6为混凝土开裂时截面及截面应变示意,其中t为钢管壁厚,hc为截面受压区的高度。此时截面处于弹性阶段,截面中性轴与形心轴重合。当混凝土拉应变为εt0时,Ms和Mc分别为 (3) (4) 图6 混凝土开裂时截面及应变分布 (2)近弹性工作阶段 受拉区混凝土开裂退出工作,钢管-混凝土截面的中性轴向受压区移动,随弯矩的增大,钢管受拉区下边缘首先达到屈服,而受压区混凝土未达到极限压应变。在此阶段不考虑受拉区开裂混凝土的作用,该阶段的截面及截面应变分布如图7所示,其中,εc1为受压区钢管的压应变,可根据应变线性分布关系求得。 图7 钢管受拉屈服时截面和应变分布 该阶段的抵抗弯矩Ms和Mc分别为 (5) (6) (3)弹塑性阶段 钢管受拉区发生屈服后,受压区钢管应力随着荷载继续增加直至达到屈服强度fy,钢管受拉区的屈服段向上扩展,受拉区钢管部分屈服应变示意如图8所示,图中y为钢管侧壁受压(拉)屈服点到中性轴的距离,可取y=hc。 此时截面的抵抗弯矩可以表示为 (7) (8) 图8 钢管受拉屈服时截面和应力应变分布 弯矩继续增大后,钢管的屈服范围进一步增大,根据全塑性理论,截面达到全塑性破坏时的应变分布如图9所示。截面的极限弯矩表达式为 图9 全塑性破坏时截面和应变分布 (10) 3.2.2 自由滑移状态 (1)混凝土开裂前阶段 图10为界面自由滑动时钢管-混凝土截面示意。 图10 混凝土开裂时截面与中性轴位置 对于不考虑界面粘结力的钢管混凝土,钢管与核心混凝土绕各自中性轴弯曲,钢管与混凝土的受压区高度均为h/2。因此,钢管截面的抗弯承载力计算式同式(4),而混凝土在受拉区发生开裂时的弯矩为 (11) (2)近弹性工作阶段 根据假设,由于不考虑受拉开裂混凝土的作用,核心混凝土截面的中性轴不断上移,而钢管截面的中性轴始终保持与其几何形心重合,并围绕其发生弯曲变形。图11为界面自由滑移时,钢管与开裂后混凝土的截面,由于此时核心混凝土与钢管变形不再一致,此阶段的抗弯承载力只需按式(12)计算钢管截面的抗弯承载力即可。 图11 混凝土开裂后截面与中性轴位置 (12) (3)弹塑性阶段 钢管-混凝土界面在自由滑移状态下,钢管的拉压屈服同时发生,则钢管截面在达到全塑性破坏时的抗弯承载力可根据式(8)计算得出。 A4与A10截面简化如图12所示。 图12 计算截面(单位:mm) 材料参数:钢管为Q345BZ钢制作,弹性模量Es=210 GPa,屈服强度为345 MPa;核心混凝土为C40混凝土,σc=26.8 MPa,σt=2.39 MPa,弹性模量为Ec=32.5 GPa。 计算得到的A4与A10两截面在钢管与混凝土完全连接与自由滑移两种极限状态下的截面抗弯承载力列于表1中。 表1 截面抗弯承载力 MN·m 由表1可得:界面自由滑移状态下截面的极限抗弯承载力约为完全连接状态的80%左右,并且通过抗弯承载力计算公式和A4与A10两截面的抗弯承载力计算结果可得:截面的高宽比越大,其比值越小。因此,对于高宽比较大的截面,应适当考虑界面连接状态对承载能力的影响。 在实际应用中,钢管与混凝土界面间存在的黏结力和摩擦力,保证了在较低荷载水平下两种材料共同受力、共同变形,充分发挥组合结构1+1>2的优良受力性能。但是,随着荷载的不断加大,当界面间的剪应力超过黏结力之后,钢管与混凝土之间的连接失效。由于混凝土与钢管变形的不协调性,混凝土会沿着钢管的接触面发生错动。从而钢管与混凝土之间的组合作用转变为叠合作用,相比完全连接的状态,其承载能力势必会降低。 当混凝土与钢管发生错动时,界面剩余黏结力与截面受力满足 Nst=Nsc+Ncs (13) 式中,Nst为受拉区钢管合力;Nsc为受压区钢管合力;Ncs为钢管与混凝土界面的黏结力。Ncs=Acsτu,τu为钢管与混凝土界面的平均抗剪黏结强度,可根据GB50936—2014《钢管混凝土结构技术规范》取值,Acs为钢管与混凝土的接触面积,其为界面连接失效高度hf的函数。 混凝土与钢管界面连接失效一般发生在弹塑性阶段,即当受拉钢梁开始屈服,由于钢与混凝土变形不一致而导致的界面剪应力过大。因此界面连接失效高度hf小于该阶段混凝土受压区的高度。为得到不同界面状态钢管与混凝土抗弯承载能力的差别,计算得到了钢管壁厚t=20 mm时,τu取值0.4 MPa时,图12(a)中的A4截面在3种界面状态下的抗弯承载能力,结果如表2所示。 表2 不同界面状态截面抗弯承载力 MN·m 由计算结果可知:(1)考虑钢管与混凝土之间的黏结力作用时,截面的抗弯承载力约为完全连接状态的93%;(2)在近弹性阶段即结构在实际应用中的受力阶段,其极限抗弯承载力与完全连接状态下相同,因此,对于高宽比满足一定条件的情况下,钢管-混凝土截面可按照完全连接进行截面的抗弯承载力计算;(3)相比较自由滑移状态下截面的极限弯矩,考虑黏结作用时的截面极限弯矩增大了13%左右,自由滑移状态在实际工程结构中很难出现。 为分析钢管壁厚对截面承载能力影响,进行了8种厚度下截面抗弯承载能力计算,计算结果如表3所示,拟合曲线如图13所示。 由计算结果可得,两种界面状态下的极限抗弯承载力均随着管壁厚度的减小而下降,且呈线性衰减规律。 以太原市下穿火车站的管幕工程为分析对象,利用Ansys建立简化的数值分析模型,对管幕结构的静力受力特性进行分析。数值分析模型 表3 不同壁厚钢管截面抗弯承载力 MN·m 图13 不同界面状态下管壁厚度与抗弯能力关系曲线 根据实际结构建模,具体尺寸如图14所示,纵向长度5 m。结合结构尺寸和计算成本,网格大小设为0.5 m,网格划分如图15所示。 图14 模型尺寸(单位:mm) 图15 模型网格划分 管幕结构中钢管采用Solid65实体单元,混凝土采用Solid 45单元,通过在钢管与混凝土之间设置弹簧Combine39单元,并按照组合结构中完全连接的设计方法设置弹簧单元的横向刚度,使钢管与混凝土完全连接。模型中通过对管幕结构的底面单元设置刚度很大的竖向弹簧来模拟地层的竖向支撑作用,作为有限元模型的边界条件。 材料的参数与本构关系同前,弹簧单元采用Ollgaard本构模型。 图16 荷载分布示意 根据工程实际覆土容重,有限元分析时初级荷载(A=1)取值通过γ=19 kN/m3,h=1 m计算得到。之后,通过改变荷载系数的取值对结构施加成比例增长的荷载。有限元计算结果表明,当荷载系数A=45时,混凝土的最大拉应力达2.61 MPa,如图17所示,钢管内混凝土受拉边缘开裂。 图17 混凝土开裂时结构应力云图(单位:Pa) 当荷载系数增大到135时,钢管的最大拉应力为310.0 MPa,接近其屈服强度,此时混凝土已破坏,钢管开始屈服,达到极限状态。钢管应力云图如图18所示。 图18 极限状态钢管应力云图(单位:Pa) 对比有限元计算得到的截面A10在不同极限状态下的抗弯承载力与理论计算结果如表4所示。通过表4可知,理论计算结果较有限元分析结果偏大8%,这主要是由于理论计算假设纯弯状态与结构实际受力状态差异,以及对有限元模型突鼓处进行平面简化造成的。 表4 抗弯承载力对比结果 MN·m 同时,为得到该结构的变形特性,图19给出了不同荷载系数A与结构A4截面底部位置处的竖向位移关系曲线。通过荷载系数-位移关系曲线,在初始加载阶段,荷载系数-位移为线性关系,结构刚度最大;随着荷载逐步增大,关系曲线表现出非线性,结构刚度逐渐减小。 图19 A4截面处竖向位移与荷载系数关系曲线 通过对下穿太原火车站管幕-结构典型位置构件抗弯承载能力进行理论计算和数值模拟研究,结论如下。 (1)管幕-结构法中钢管与主体混凝土界面状态对结构构件抗弯承载力有较大影响,自由滑移状态和考虑钢管与混凝土之间的黏结力作用时,其极限抗弯承载力分别约为完全连接状态的80%和93%。 (2)不同界面状态下结构构件承载能力与截面几何特征相关,截面的高宽比越大,对承载能力影响程度越大。 (3)不同界面状态下结构的极限抗弯承载力均随管壁厚度的减小而呈线性减小的规律。 (4)有限元计算表明,随着荷载增加管幕结构变形由线性向非线性变化。 本文只对构件在受弯转态下的承载能力进行了分析,今后可进一步研究其在偏心受压状态下各阶段的承载能力,以揭示其压弯承载特性。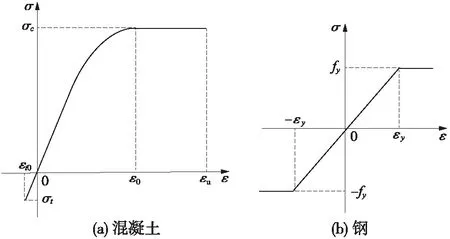




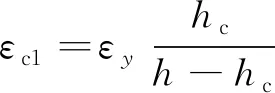
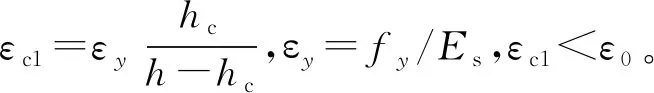








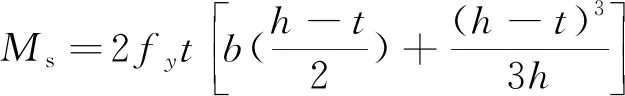
4 界面状态与钢管壁厚对截面抗弯承载力的影响分析
4.1 界面状态对截面抗弯承载力影响算例


4.2 3种界面状态抗弯承载力对比

4.3 钢管壁厚对抗弯承载力的影响
5 管幕结构受力特性简化有限元分析









6 结论
