基于山岭隧道探孔流量的富水破碎构造带水头预测方法

于晨昀,项彦勇,孙俊豪

(1.中铁工程设计咨询集团有限公司,北京 100055； 2.北京交通大学土木建筑工程学院,北京 100044)

引言

山岭隧道修建过程中，会遇到开挖面前方存在富水断层构造带[1]、高压富水断裂带[2]、富水岩溶[3-4]等富水破碎构造带的复杂地质情况。隧道施工期穿越上述不良地质时存在突水涌泥等施工风险，且隧道运营期承担的外水压力与水头高度密切相关。确定富水破碎构造带的水头高度对保障山岭隧道施工与运营安全具有重要意义。

为确保隧道穿越富水破碎构造带的施工安全，需进行超前地质预报。超前地质探孔是常用的超前地质预报手段，采用地质钻机钻孔并安装流量计，可以比较直观的探明开挖面前方钻孔所经部位的地层岩性、岩体完整程度和地下水发育情况[5-6]，连续钻探时探孔有效长度一般每循环不超过50 m。

吴建、朱彬彬等[7-8]开展隧洞涌水量预测计算及方法研究进展，杨建军[9]根据探孔的喷水距离和喷水量对可能发生突水的类型进行判断，结合喷水量及喷水距离判断突水情况并制定相应的防水方案及措施；袁真秀等[10]在圆梁山隧道高压富水地区，利用平行导洞超前探孔的涌水特征，对前方溶洞的尺度和连通性进行判断；段庆伟等[11]基于渗流理论推导出施工期隧道开挖后围岩内水压力分布的解析解，研究远场稳定水头与远场稳定水头半径的相互关系。何志军等[12]推导了含水层中椭圆形隧道的近似解析解，用于计算隧道周边水头和孔隙水压分布。姚桥矿和李明山[13]、王革纯等[14]、侯恩科等[15]分别对钻孔涌水量计算方法进行了探讨。

目前，国外针对隧道超前钻孔排水与围岩渗流相互作用问题已开展研究，如，Hong等[16]研究了超前排水钻孔的水力能力问题；Zingg & Anagnostou[17-18]在孔壁处于大气压力假设下，考虑孔壁水压变化，采用理论方法与数值模拟，研究了超前钻孔排水与围岩渗流的相互作用及其对隧道开挖面稳定性的影响。

隧道突水风险与开挖面前方水头高度密切相关[19]，但现有研究大多是关于隧道开挖面前方涌水量预测，对开挖面前方水头高度预测研究较少。考虑围岩渗透性的影响，研究提出通过探孔涌水量预测隧道开挖面前方富水破碎构造带水头高度的3种预测方法：简化理论方法；轴对称稳态与瞬态渗流数值模拟方法；基于稳态渗流数值模拟数据的近似拟合方法。

1 探孔-围岩稳态流动的广义伯努利理论

1.1 探孔稳态流动的无渗漏管流理论

超前探孔壁面稳定，围岩渗透系数较小，可近似地认为探孔与围岩之间无水力联系，如图1所示。假设探孔内水流为无渗漏的满管水流，利用伯努利方程[20]，可以得出

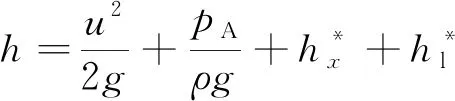
(1)

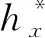
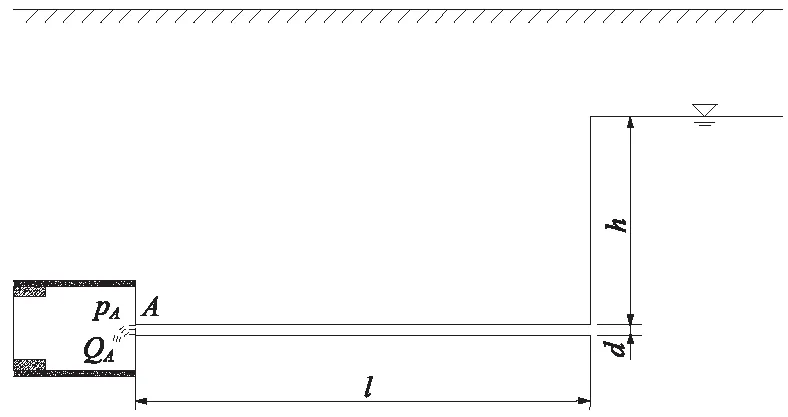
图1 超前水平探孔的无渗漏管流模型

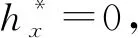
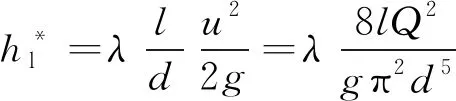
(2)

式中，Q为探孔出水口流量，Q=uπd2/4；l和d分别为探孔的有效长度(隧道开挖面到前方富水破碎构造带边界的水平距离)和直径；λ为沿程阻力系数，其与管流的流态(层流或紊流)和孔壁的粗糙度有关。根据流体力学理论[20]，采用雷诺数Re=ρud/μ来判别层流或紊流(μ为水的动力黏度，对于常温地下水，可取μ=1.005×10-3Pa·s)，一般以Re=2 300作为层流与紊流的分界，当Re<2 300时管流为层流，沿程阻力系数为λ=64/Re；当Re>2 300时管流为紊流，可根据雷诺数Re和管壁相对粗糙度e/d(e为管壁粗糙度)由莫迪(Moody)图确定沿程阻力系数λ值。

假设管流在近端为自由排水，压强pA=0，并将式(2)代入式(1)，可得

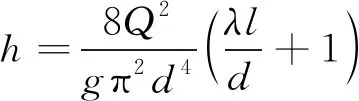
(3)

由式(3)可见，探孔的远端水头分别与流量平方、长度、沿程阻力系数成正比。

1.2 探孔-围岩稳态流动的均匀渗漏管流理论

超前探孔壁面稳定，围岩渗透系数较大，探孔与围岩之间的水力联系不可忽略，如图2所示。假设探孔内的水流为有渗漏的满管水流，基于伯努利方程，可以得出

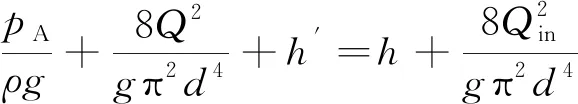
(4)

式中，h′为管流的平均水头损失；Qin为管流在远端的流量。其余符号的定义同前。

基于质量守恒原理，Qin=Q+Ql，代入式(4)，可得

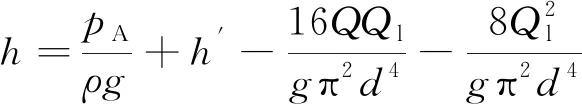
(5)

式中，Ql为管流全长的渗漏流量。

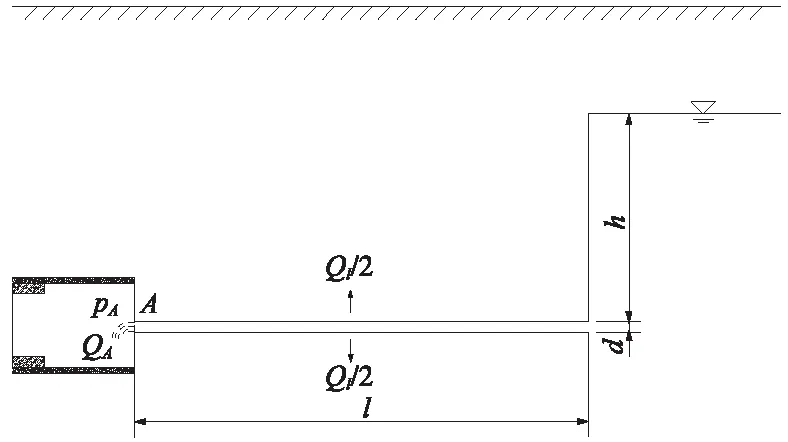
图2 探孔-围岩的均匀渗漏管流模型

2 探孔-围岩稳态渗流数值模拟与参数分析

2.1 探孔-围岩轴对称稳态渗流有限元模型

探孔壁面稳定，如前方富水破碎带水头较高，则地下水重力梯度与压力梯度的影响相比很小，可以忽略不计，近似认为水力梯度等于水压梯度，渗流关于探孔轴线对称。

采用有限元软件Midas GTS NX，建立任意轴对称截面的稳态渗流有限元模型，如图3所示。其中，隧道高12 m，探孔直径和长度分别为0.1 m和30 m，模型上、下边界到探孔轴线的距离均为50 m，富水破碎构造带位于探孔的远端，水头高度50 m。网格的密集程度与水力梯度的分布特征相对应，较高水力梯度的区域采用较密集网格，较低水力梯度的区域采用较稀疏网格。

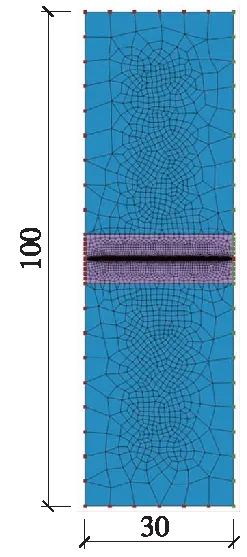
图3 探孔-围岩稳态渗流的轴对称有限元模型(单位：m)

基于渗流的轴对称特征，设定有限元模型边界条件为：(1)左边界，压力水头为零；(2)右边界，在钻孔远端(入水口)的压力水头为50 m，其他位置不透水，即探孔远端是唯一的入水口；(3)上边界，不透水；(4)下边界，不透水。

有关计算参数如表1所示，其中，d为探孔直径；k为围岩的渗透系数；lr为探孔的有效长度；h为水头高度。

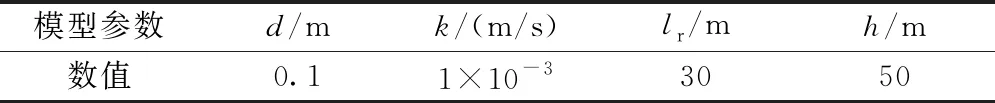
表1 有限元模型参数

由于实际探孔出水量远大于围岩渗水量，将探孔模拟为渗透性远高于围岩渗透性的多孔介质，则探孔节点的轴向达西流速qx与探孔截面积的乘积即为探孔出水口流量Q，Q=qxπd2/4。

2.2 数值模拟的参数影响分析

探孔-围岩的压力水头分布云图如图4所示，其中探孔出水口压力水头为0 m，探孔入水口压力水头为50 m，表明模型的流动达到了稳态流动。

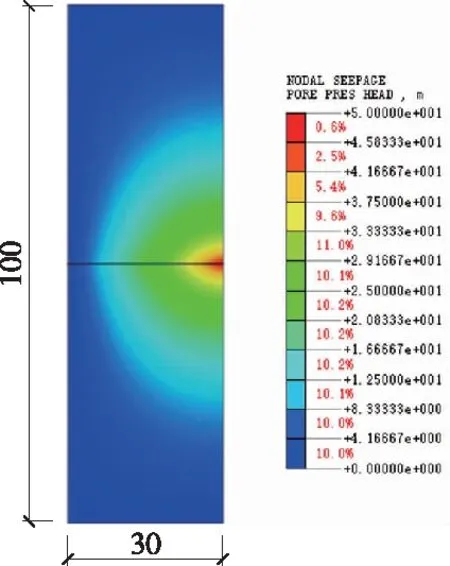
图4 稳态压力水头云图(单位：m)

图5为探孔上、下边界壁面上法向(y轴)达西流速qy沿探孔轴线(x轴)的分布曲线。x轴和y轴原点均位于探孔在隧道开挖面处中心，qy为正值时表示向上流动、为负值时表示向下流动。由图5可见，探孔内水流从进水口处开始向围岩渗漏，渗漏速度随流动距离的增加(x减小)而逐渐减小至零，之后探孔内的水流得到围岩水流的补给(负渗漏，流速较低)，补给速度随流动距离的增加(x减小)而逐渐增加，至出水口处达到最大值，零渗漏点到出水口的距离为17.7 m(与有效长度之比为0.59)。

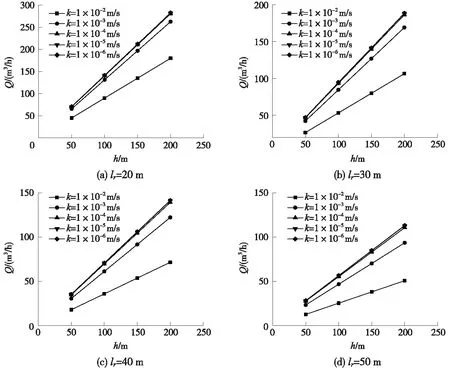
图7 不同探孔有效长度lr的Q-h曲线(稳态)

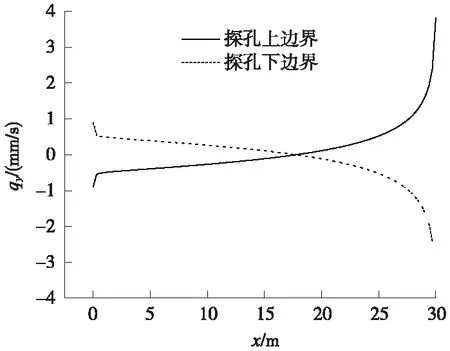
图5 探孔壁面法向(y轴)稳态达西流速沿轴线(x轴)分布曲线

为进行参数影响分析，根据上述数值模拟结果，考虑探孔-围岩内稳态渗流模型如图6所示，其中，A为探孔在隧道开挖面处截面；B为探孔在富水破碎构造带近边界处截面；C为探孔在富水破碎构造带内部某处截面；O为探孔在渗漏流量为零处截面(位置待定)。探孔内的水流在OA段为负渗漏(即得到围岩水流补给)，在OB段为正渗漏(即向围岩渗漏)，BC段对AB段及围岩内的流动无影响。

分别取水头高度h为50，100，150，200 m；探孔围岩渗透系数k为10-2，10-3，10-4，10-5，10-6m/s；探孔有效长度lr为20，30，40，50 m，共计4×5×4=80个工况进行数值模拟，分析参数对探孔出水口流量Q与水头高度h关系的影响特征。

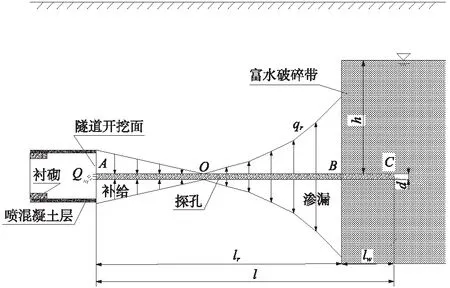
图6 探孔-围岩内的稳态渗流模型

图7为探孔有效长度lr分别取20，30，40，50 m时，与不同围岩渗透系数值相对应，探孔出水口流量Q与水头高度h之间的关系曲线。可见，对于设定的k和lr，Q随h的增大呈线性增大趋势；对于设定的lr，Q随k的减小而增大，随h增大的速率同时增大；当k取值为10-4m/s及以下时，对Q-h关系基本没有影响。

图8为水头高度h=50 m时，与不同围岩渗透系数k值相对应，探孔出水口流量Q随探孔有效长度lr的变化曲线。可见，对于设定的h和k，Q随lr的增大以逐渐降低的速率非线性地减少；对于设定的h，Q随k减小而增大；当k取值为10-4m/s及以下时，对Q-lr关系基本没有影响。

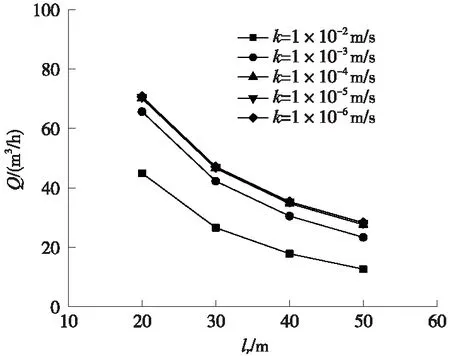
图8 水头高度h=50 m时Q-lr曲线(稳态)

图9为围岩渗透系数k不同取值时，探孔水流补给段长度比lOA/lr随前方富水破碎构造带水头h的变化。可见，对于设定的k值，lOA/lr随h的增大以逐渐降低的速率非线性地减小；对于设定的h值，lOA/lr随k减小呈非线性地减小趋势。

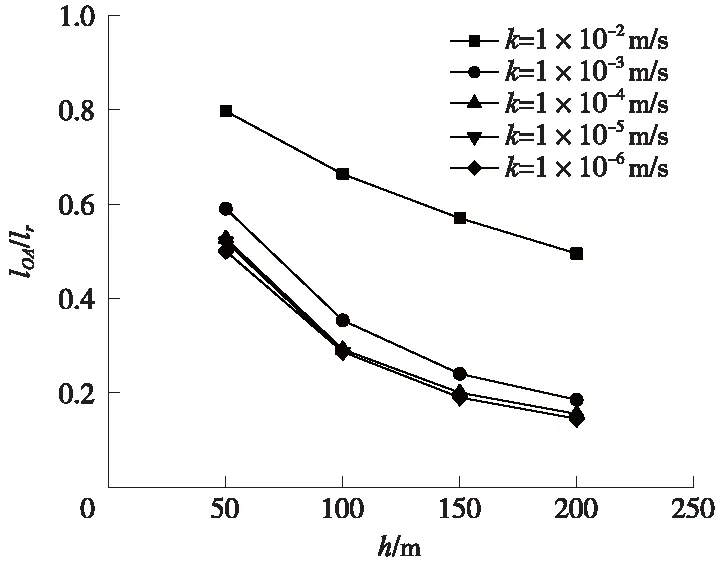
图9 lOA/lr-h-变化曲线(稳态)

图10为围岩渗透系数k不同取值时，探孔出水口流量Q与入水口流量Qin之比。可见，对于设定的k值，Q/Qin与h无关；当k减小时，Q/Qin增大(注意，Q/Qin必须≯1)；当k取值为10-4m/s及以下时，Q/Qin趋于1，即探孔出水口流量与入水口流量相等，基本上无渗漏与补给。

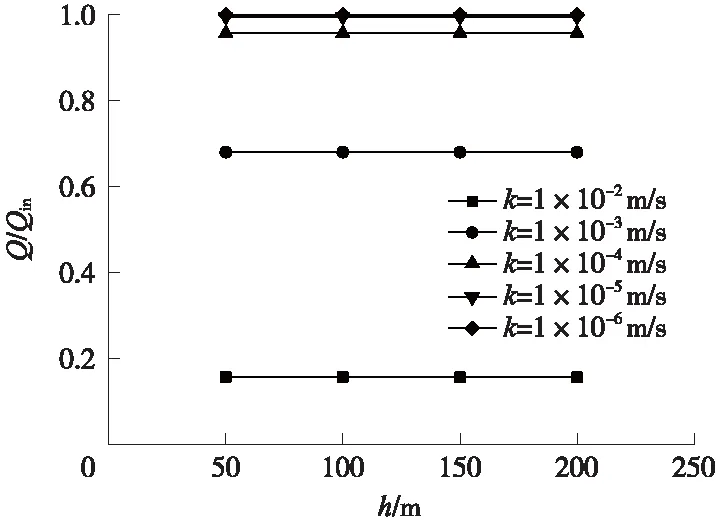
图10 Q/Qin随h的变化曲线(稳态)

综上所述，水头高度h与探孔出水口流量Q之间，因受达西渗流模型所控而呈线性关系；探孔远端渗漏段长度、渗漏流量和探孔近端补给段长度、补给流量均受制于探孔有效长度lr和探孔围岩渗透系数k，对h-Q关系的斜率及其变化特征产生影响。

3 探孔稳态出水流量-前方富水破碎构造带水头高度拟合式

3.1 拟合式的建立

由上节数值模拟结果可见，对于给定的探孔有效长度lr和围岩渗透系数k，探孔出水口流量Q与水头高度h之间呈线性正比例关系，一般可表示为

Q=α(lr，-lgk)h

(6)

式中，α(lr，-lgk)为比例系数，是探孔有效长度lr和探孔围岩渗透系数k的函数(当流量单位以m/s表示时，围岩渗透系数k值较小，为便于拟合，将k表示成常用对数的负数)。

利用上节数值模拟所得数据，采用二元二次多项式的函数形式，通过最小二乘法优化，得到Q与h之间的拟合关系式

(7)

式中，c1、c2、c3、c4、c6、c6代表拟合系数，如表2所示。

表2 拟合系数取值

3.2 拟合式与无渗漏管流理论公式对比

考虑常温地下水，把无渗漏管流理论公式(3)与拟合式(7)进行对比。有关参数取值如表3所示(围岩渗透系数取值很小)，计算结果对比如图11所示。

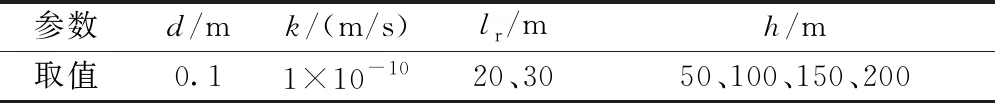
表3 对比数值拟合式与无渗漏管流理论式的参数取值

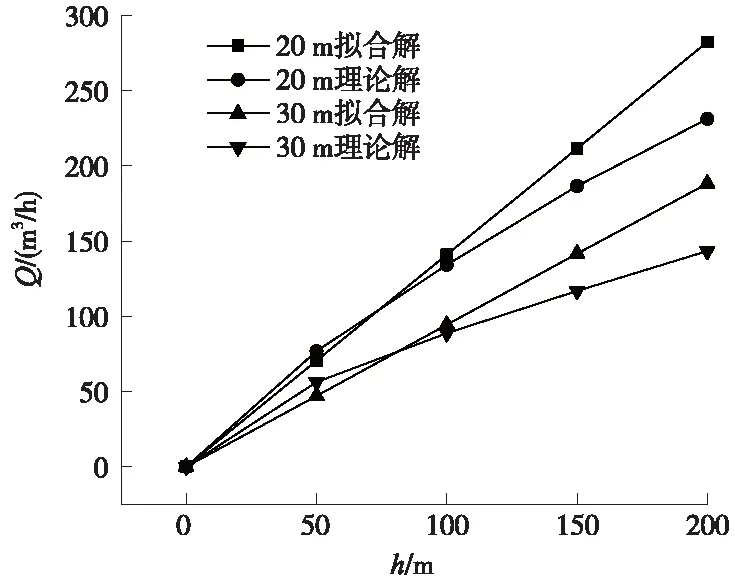
图11 不同探孔有效长度lr(k很小)拟合式(7)与理论式(3)对比曲线

由图11可见，如果围岩渗透系数值很小，无论探孔有效长度lr为何值，只要水头高度h≯100 m，拟合式(7)与理论式(3)间无显著差别。但如果h超过100 m，则由拟合式(7)得到的探孔稳态出水流量明显大于理论式(3)，且差别随h的增大而逐渐增大。

4 探孔瞬态涌水的数值模拟与分析

采用图3所示的有限元模型及边界条件，按表1选取参数值，对探孔-围岩内的轴对称瞬态渗流进行数值模拟，分析探孔出水口流量与水头高度的关系和稳态时间与岩体渗透系数的关系。其中，如果在1个时间步长内，探孔出水口流量的相对变化率≯0.5%，即认为流场已经达到稳态。

如图12所示，在任意给定时刻，探孔出水口流量Q与水头高度h间均为线性正比例关系，且Q-h的斜率随着时间t的增大而增大，在稳态时达到最大值。

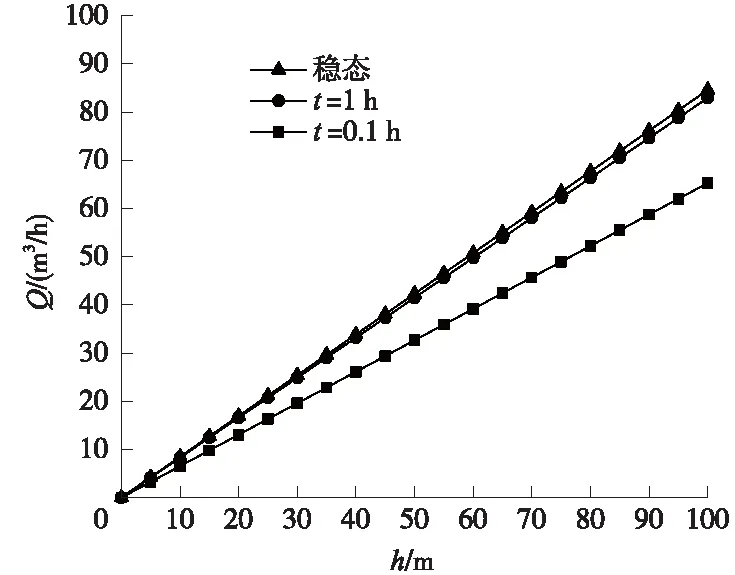
图12 不同时刻的Q-h关系曲线

如图13所示，对于给定的探孔有效长度lr，随着围岩渗透系数k增大，达到稳态所需的时间t先增加、后减少；且随着lr值增大，渗漏和补给的作用增大，对稳态时间的影响也越显著。

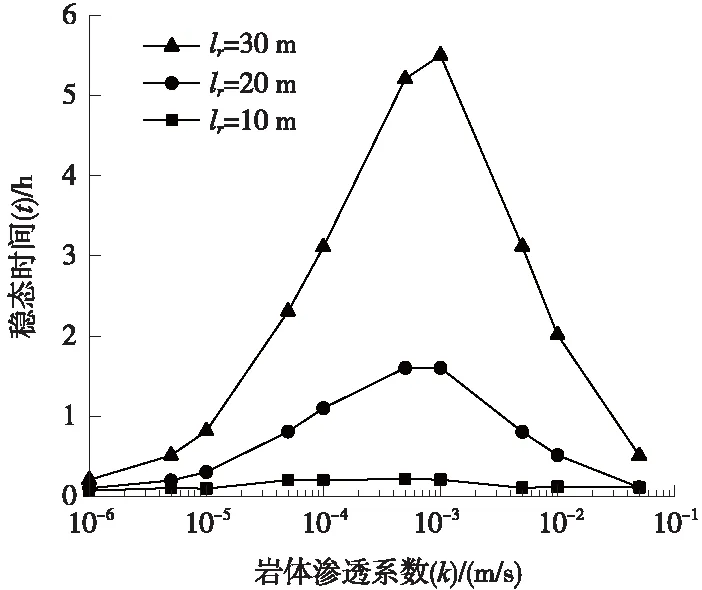
图13 围岩渗透系数对达到稳态所需时间的影响

5 结论

在山岭隧道工程中确定富水破碎构造带的水头高度对降低隧道施工期突水突泥等灾害风险，保证隧道运营期衬砌结构安全具有重要意义。针对隧道超前探孔出水口流量Q与前方富水破碎构造带水头高度h间的关系问题，基于伯努利方程得到了简化理论关系式；通过隧道开挖面前方富水破碎构造带高水头工况下探孔-围岩轴对称稳态及瞬态渗流的数值模拟，得到了基于模拟结果的拟合关系式，进行参数影响分析，并与简化理论关系式进行对比。通过研究得到以下结论。

(1)探孔稳态或瞬态出水口流量与水头高度之间呈线性正比例关系，比例系数随探孔有效长度和围岩渗透系数的增大而减小。

(2)当围岩渗透系数较大时(>10-4m/s)，探孔内的稳态水流出现两段不同的边界面渗流情况，一段是在远端一定长度内的渗漏，另一段是在近端一定长度内的补给。

(3)围岩渗透系数较小时(<10-4m/s)，对探孔稳态出水流量与水头高度间关系无影响；

(4)探孔-围岩渗流由瞬态达到稳态所需的时间与水头高度无关，但随围岩渗透系数的增大呈先增大、后减小趋势，且这种影响随探孔有效长度的增大而增强。

(5)对于探孔有效长度，如围岩渗透系数很小，当水头高度≯100 m时，拟合关系式与简化理论关系式之间没有显著差别，但当水头高度超过100 m，拟合关系式的探孔稳态出水流量明显大于简化理论关系式出水流量。