基于动力学分析的悬挂式单轨线路空间线形研究
2021-05-17寇峻瑜余浩伟
寇峻瑜,谢 毅,余浩伟,罗 圆,肖 杰
(1.中铁二院工程集团有限责任公司,成都 610031; 2.四川高新轨道交通产业技术研究院,成都 610031)
在传统轮轨铁路中,为保证列车运行平稳性和旅客乘坐舒适性,同时考虑钢轨加工制造精度、施工难度和养护维修等因素,平面圆曲线一般情况下不宜与竖曲线重叠设置,缓和曲线不应与竖曲线重叠设置[1]。
悬挂式单轨作为一种近几年兴起的新型轨道交通制式[2-3],在车辆动力学性能[4-5]、限界[6]、曲线通过[7-8]、轨道梁结构特性[9-10]、参数优化[11]等方面的研究已有较多,且主要以国外既有车辆为分析对象。针对线路平、纵断面参数取值,仅有部分文献提出舒适度控制指标[12]、平面圆曲线半径[13]、缓和曲线长度[14],而关于平、竖曲线重叠设置问题尚未涉及。由于悬挂式单轨车辆在箱形轨道梁内实现走行和导向[15],与传统轮轨制式存在差异,其在空间线形条件下的动力响应必定有所不同。因此,结合国内研发的悬挂式单轨车辆,对竖曲线与平面圆曲线、缓和曲线在不同重叠情况下的动力学特性进行研究,进而提出悬挂式单轨线路平、竖曲线重叠设置的相关建议。
1 悬挂式单轨车辆系统动力学模型
采用多体动力学软件Universal Mechanism建立图1所示的悬挂式单轨车辆系统动力学模型。在该模型中,车体、转向架构架、摇枕、走行轮和导向轮等均视为刚体,总共25个刚体,共计60个自由度,各刚体的自由度详见表1,其中“√”表示有该自由度。关于模型的详细描述可参考文献[16-17]。模型中分别定义车辆前进方向、水平向左、垂直轨面向上为x、y、z方向。
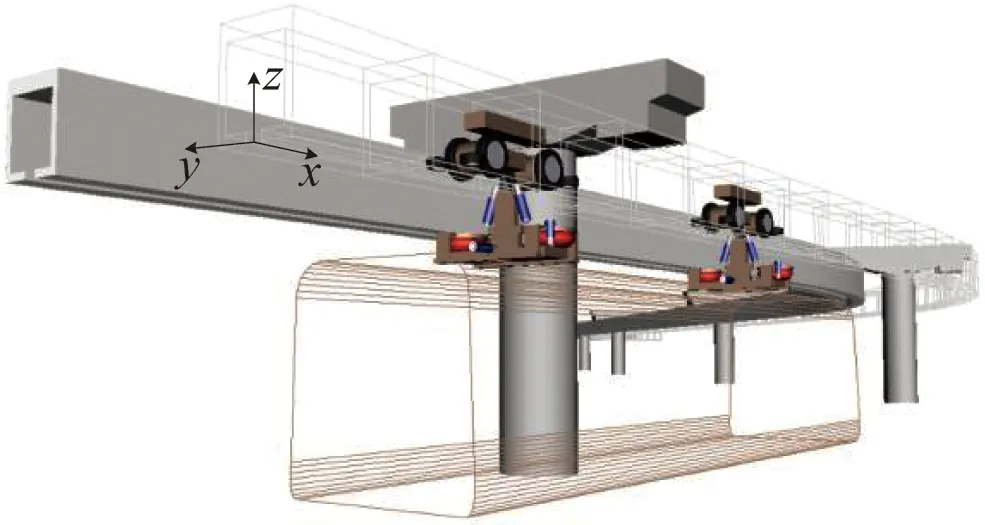
图1 悬挂式单轨车辆系统动力学模型
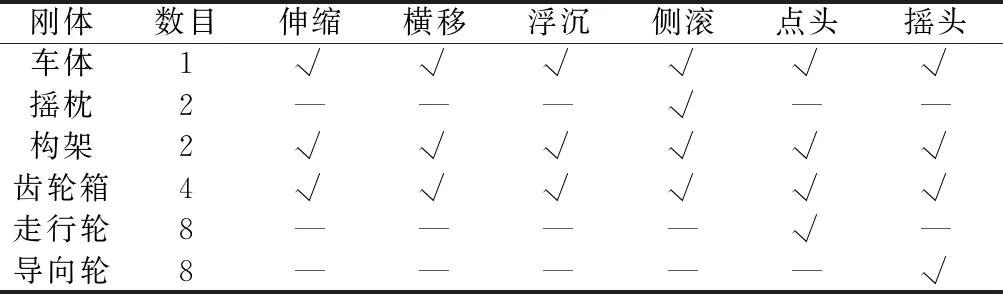
表1 悬挂式单轨车辆系统自由度
结合实际,悬挂式单轨车辆系统轮胎模型采用橡胶轮胎。考虑到走行轮和导向轮在轨道梁内走行过程中的侧偏角度较小,轮胎模型采用基于弹性地基梁的Fiala轮胎模型[18]。模型中横向减振器、垂向减振器、抗摇摆减振器的力学行为采用与车辆运行速度V正相关的力元模拟,空气弹簧和牵引拉杆则考虑为线性力元,刚度和阻尼均为常数。
2 竖、圆曲线重叠时的动力学分析
为了衰减因线路曲率变化而产生的振动,并保证前后振动不叠加,通常在两相邻缓和曲线之间设置夹直线或圆曲线、两相邻变坡点之间设置夹坡段[19]。针对平面圆曲线与竖曲线在不同位置处重叠,研究悬挂式单轨车辆通过时的动力响应,线路平、纵断面示意如图2所示,具体线路参数详见表2。为便于分析平、竖曲线下的振动叠加,轨道梁不考虑不平顺激励。
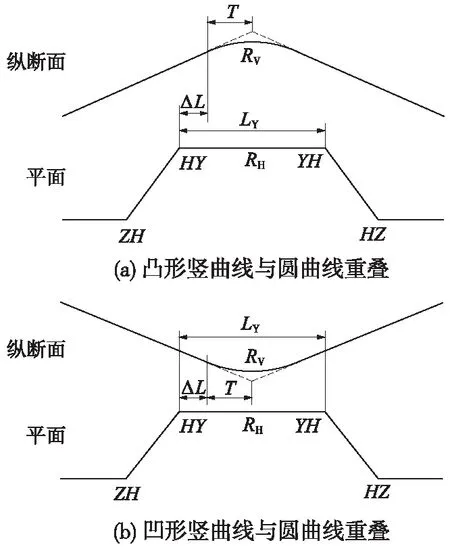
图2 竖曲线与圆曲线重叠示意

表2 竖、圆曲线重叠线路设计方案参数
图2中T表示竖曲线切线长,ΔL表示竖曲线起(终)点与缓圆点(圆缓点)之间的距离。理论上,当ΔL=0 m时,平面缓圆点处产生的振动与竖曲线起点处的振动完全叠加,此时对列车运行安全性和旅客舒适度的影响最不利;当ΔL>0 m时,平面缓圆点处产生的振动衰减一部分后再与竖曲线起点处的振动叠加。鉴于列车在凹形竖曲线与凸形竖曲线上垂向动力响应的差异性[20],同时考虑了圆曲线与凹形、凸形竖曲线重叠情况。
2.1 竖、圆曲线完全重叠
首先,将平面圆曲线与竖曲线完全重叠设置,即ΔL=0 m。图3~图7展示了仅有平面曲线、圆曲线分别与凹形和凸形竖曲线重叠3种线路条件下的动力响应对比。
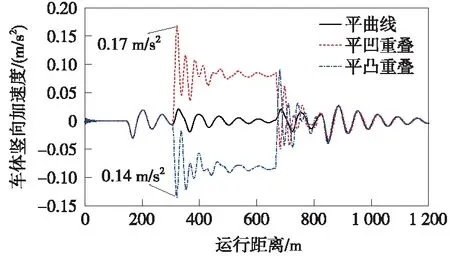
图3 竖、圆曲线重叠对车体竖向加速度的影响规律
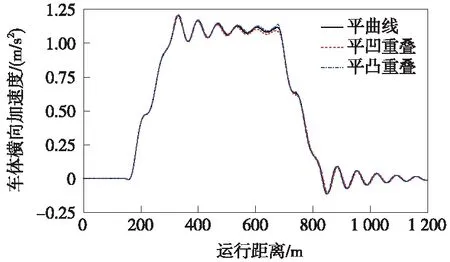
图4 竖、圆曲线重叠对车体横向加速度的影响规律
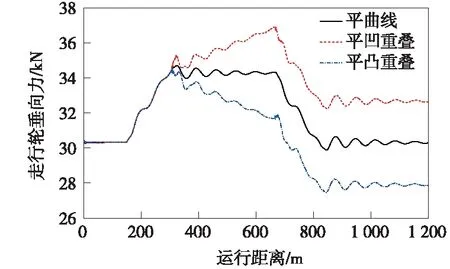
图5 竖、圆曲线重叠对走行轮垂向力的影响规律
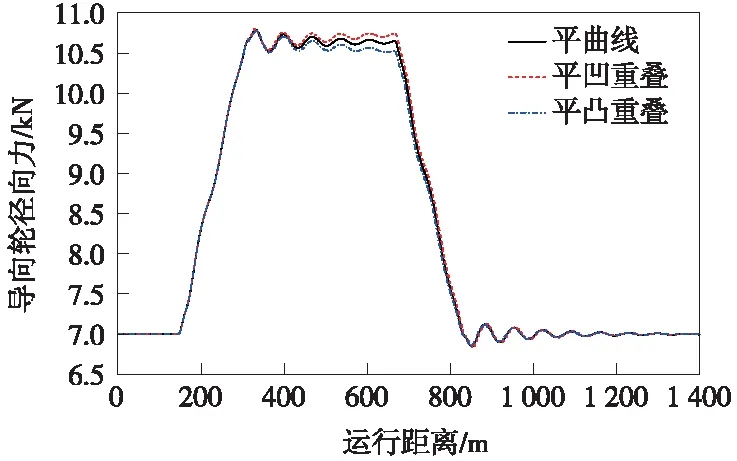
图6 竖、圆曲线重叠对导向轮导向力的影响规律
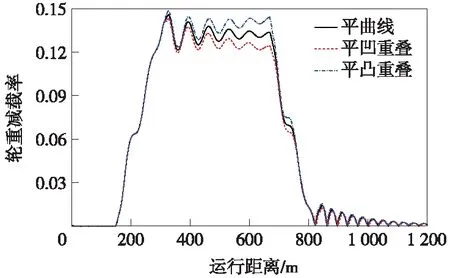
图7 竖、圆曲线重叠对轮重减载率的影响规律
从图3~图7可以看出,相比平曲线工况下的结果,竖、圆曲线重叠对垂向振动指标(如车体竖向加速度、走行轮垂向力和轮重减载率)均有一定影响。圆曲线分别与凹曲线、凸曲线重叠时,两者产生的作用相反,前者使轮重减载率减小、走行轮垂向力增大,后者使轮重减载率增大、走行轮垂向力减小。虽然在平曲线上的竖向振动较小,但由于竖曲线起点处会产生垂向冲击,平凹和平凸曲线重叠下的竖向加速度最大值分别增大至0.17 m/s2和-0.14 m/s2,这里负号仅代表方向,下文均取绝对值。对于车体横向加速度、导向轮导向力等横向振动指标,平凹和平凸曲线重叠与平面曲线情况下的结果的差异较小。因此,除车体竖向加速度外,其余各动力学指标主要受平面曲线参数的影响,竖、圆曲线重叠对悬挂式单轨车辆动力学性能的影响不大,但应保证车体竖向加速度不超过限值。
图8给出了凹曲线、凸曲线和平凹重叠、平凸重叠情况下的车体竖向加速度对比。相比竖曲线工况下的竖向加速度最大值,由于振动叠加的作用,竖、圆曲线重叠会使得振动叠加增强或减弱。凹、圆曲线重叠下的竖向加速度最大值(0.17 m/s2)相比凹曲线的结果(0.15 m/s2)增大了13.33%,而凸、圆曲线重叠下的竖向加速度最大值(0.14 m/s2)相比凸曲线的结果(0.15 m/s2)减小了6.67%。其主要原因是,在竖曲线起点位置,平曲线上车体的竖向振动刚好到达谷底,即将朝上振动,这与凹、凸曲线工况下的加速度方向分别相同和相反,进而使得平凹、平凸曲线重叠时振动叠加分别增强和减弱。
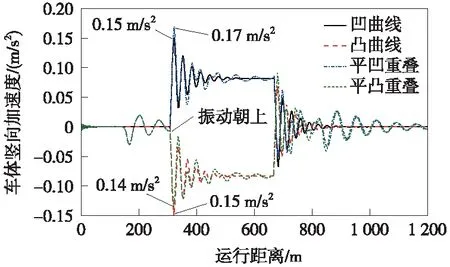
图8 竖、圆曲线重叠对竖向振动叠加的影响规律
2.2 不同重叠位置的影响
考虑竖、圆曲线不完全重叠,将竖曲线设在圆曲线中间某位置。以凹曲线与圆曲线重叠为例,图9~图12展示了ΔL=0,40 m和100 m时的动力响应对比。当竖曲线起点与圆曲线重叠位置发生变化后,除了车体竖向加速度,其余各动力学指标在不同ΔL值下的差异均很小。当ΔL=0 m时,振动叠加效果最强;当ΔL=40,100 m时,凹曲线起点处车体的竖向振动朝上,此刻平曲线上的竖向振动均朝下,凹曲线与圆曲线的振动方向相反,振动叠加减弱。ΔL分别为40,100 m时的车体竖向加速度最大值(0.14,0.15 m/s2)相比ΔL=0 m时的结果(0.17 m/s2)分别减小了17.65%和11.76%,并且ΔL=40 m时的振动叠加效果相比ΔL=100 m更强。
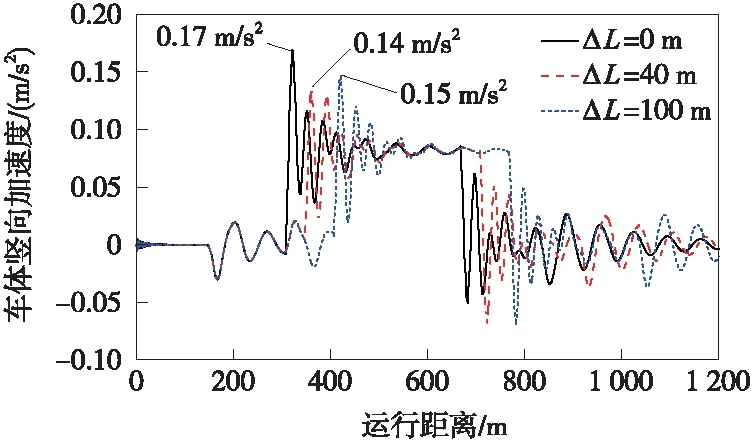
图9 不同重叠位置对车体竖向加速度的影响规律
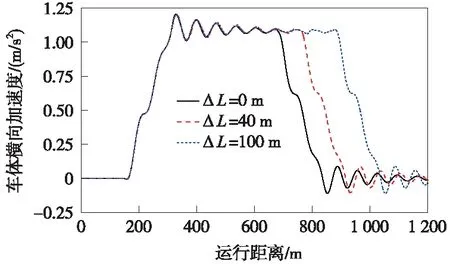
图10 不同重叠位置对车体横向加速度的影响规律
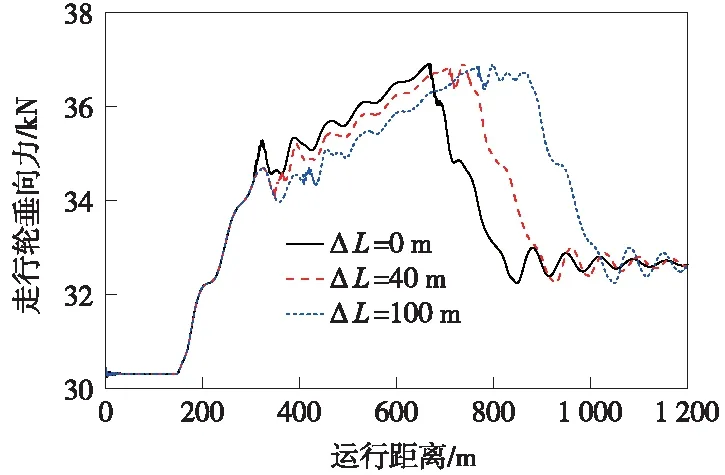
图11 不同重叠位置对走行轮垂向力的影响规律
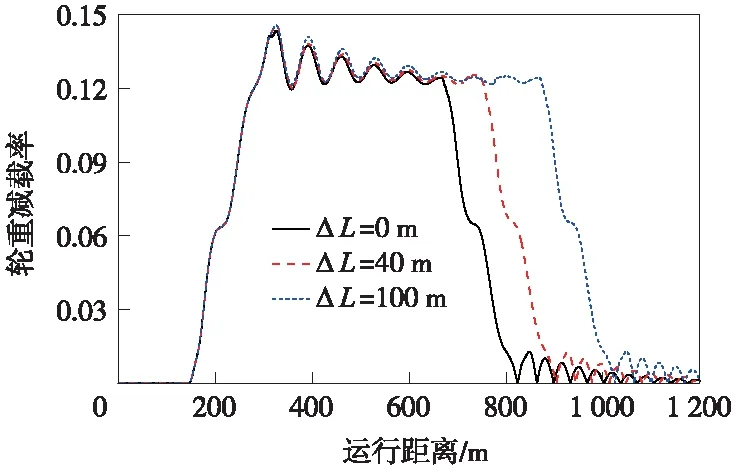
图12 不同重叠位置对轮重减载率的影响规律
图13统计了ΔL=0~400 m工况下的车体竖向加速度最大值。当凹、圆曲线起始重叠位置改变后,加速度最大值存在波动。相比凹曲线条件下的竖向加速度最大值,凹、圆曲线重叠后的结果呈波浪形变化,表明振动叠加时而增强、时而减弱,这主要取决于竖曲线起点位置和平曲线上的竖向振动的方向。结合图13可看出,当竖曲线起点与缓圆点之间间隔一定距离时,竖、圆曲线重叠会减小竖向加速度最大值,如ΔL=40,110,120 m时,且在ΔL=40 m时振动叠加减弱效果达到最大,进而改善旅客舒适度。此外,当竖曲线起点与缓圆点之间距离在300~400 m时,竖向加速度最大值变化已不大,即振动叠加效应不明显。
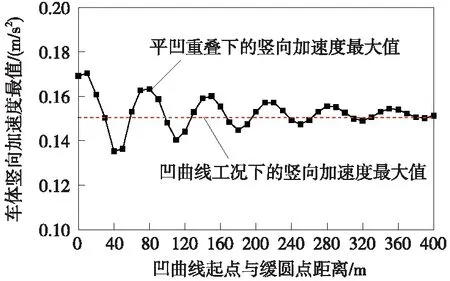
图13 不同重叠位置下的车体竖向加速度最大值
3 竖、缓和曲线重叠时的动力学分析
考虑平面曲线中前一段缓和曲线与竖曲线完全重叠,将直缓点与缓圆点之间的长度与竖曲线长度重合设置。仅有平面曲线、缓和曲线分别与凹形和凸形竖曲线重叠3种线路条件下的动力响应对比如图14~图17所示。
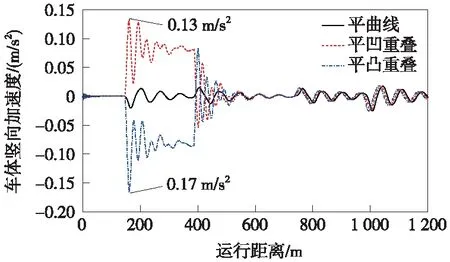
图14 竖、缓和曲线重叠对车体竖向加速度的影响规律
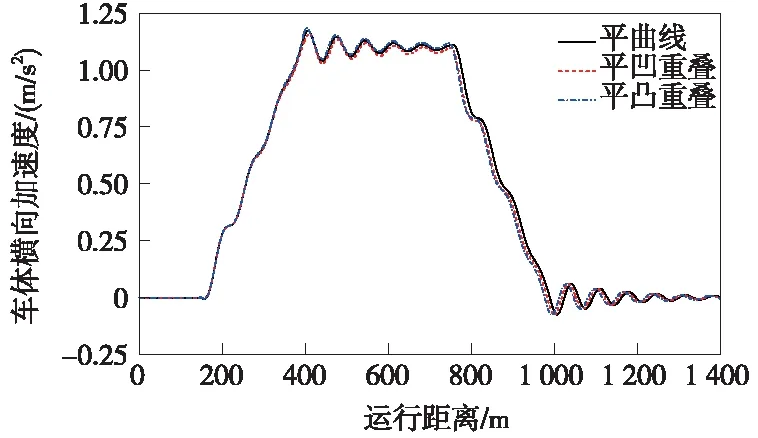
图15 竖、缓和曲线重叠对车体横向加速度的影响规律
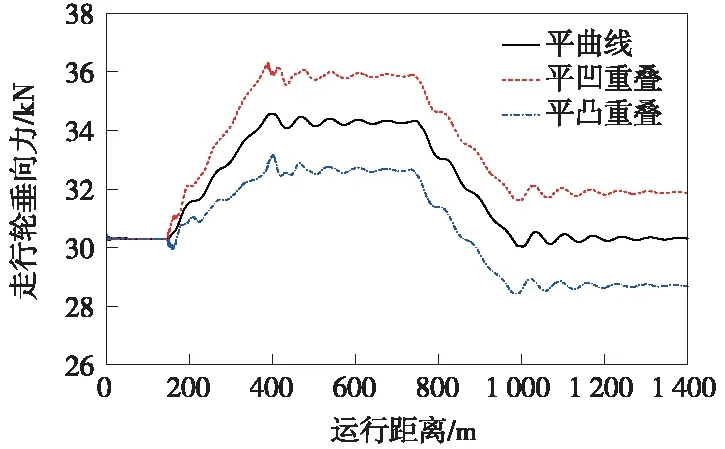
图16 竖、缓和曲线重叠对走行轮垂向力的影响规律
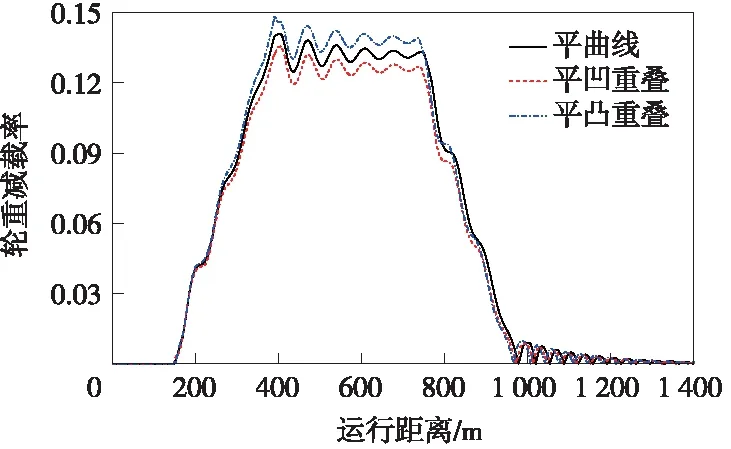
图17 竖、缓和曲线重叠对轮重减载率的影响规律
结合图14~图17可看出,缓和曲线与竖曲线重叠对车体横向加速度影响较小,而车体竖向加速度、走行轮垂向力、轮重减载率等指标均有改变,这与竖、圆曲线重叠工况下的变化趋势类似。缓和曲线分别与凹曲线、凸曲线重叠时,两者产生的作用相反,前者使轮重减载率减小、走行轮垂向力增大,后者使轮重减载率增大、走行轮垂向力减小;由于在竖曲线起点位置存在垂向冲击,平凹、平凸曲线重叠下的竖向加速度最大值分别增大至0.13 m/s2和0.17 m/s2。因此,若仅从车辆动力学性能角度考虑,竖曲线与缓和曲线可以重叠设计,但鉴于轨道梁加工制造、养护维修等因素,竖曲线与缓和曲线仍不宜重叠设置。
图18给出了凹曲线、凸曲线和平凹重叠、平凸重叠情况下的车体竖向加速度对比。由于缓和曲线段存在竖向振动,竖曲线与缓和曲线重叠也会增强或减弱竖曲线上的振动。根据图14易知平面缓和曲线起点处振动方向朝下,与凹、凸曲线起点处的振动方向分别相反和相同,则振动叠加分别减弱或增强,因此,凹曲线与缓和曲线重叠下的竖向加速度最大值(0.13 m/s2)相比凹曲线的结果(0.15 m/s2)减小了13.33%,而凸曲线与缓和曲线重叠下的竖向加速度最大值(0.17 m/s2)相比凸曲线的结果(0.15 m/s2)增大了13.33%。
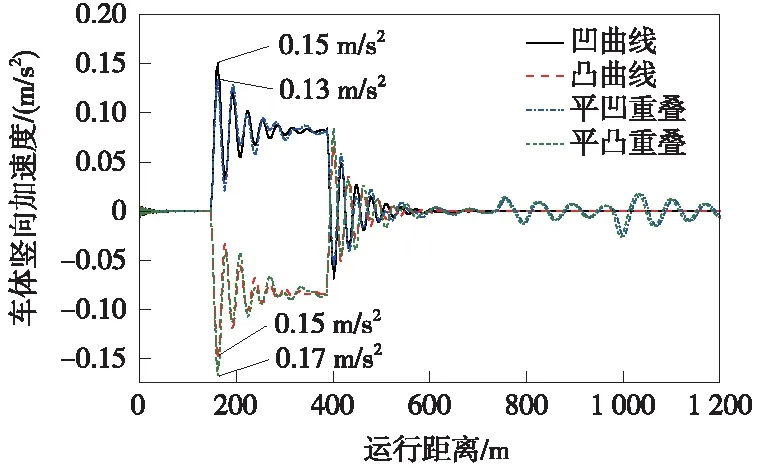
图18 竖、缓和曲线重叠对竖向振动叠加的影响规律
4 结论
(1)平、竖曲线重叠对横向振动指标影响可以忽略,对垂向振动指标影响较大,尤其是车体竖向加速度,平、竖曲线重叠设置应保证人体竖向舒适度要求。
(2)平、竖曲线重叠后的振动叠加增强或减弱效应取决于竖曲线变坡点与平面曲线上的竖向振动方向是否一致,方向相同则叠加增强,相反则叠加减弱。当竖曲线变坡点与平面曲线起终点间隔距离增大到一定值后,振动叠加效应可忽略不计。
(3)从动力学仿真角度分析,平、竖曲线重叠对悬挂式单轨车辆动力学性能的影响较小,平面圆曲线、缓和曲线与竖曲线可以重叠设计。
