一种高增益直流变换器的运行原理及数学建模

周雷

(国网宁夏电力有限公司电力科学研究院，宁夏 银川 750011)

新能源作为一种清洁、高效、绿色、可持续的能源而备受国内外关注[1-3]，其在能源结构中的比重也逐年增大[4-6]。新能源发电主要包括光伏、风电及燃料电池发电等[7]，在光伏与燃料电池发电领域中，由于光伏电池和燃料电池的输出电压较低，为与高压直流母线电压等级相匹配[8]，需要使用升压直流变换器对电源侧的输出电压进行升压。

经典Boost直流变换器因其结构简单而被广泛应用于各种场合，但其电压增益由于开关器件自身特性而受到制约，无法实现较大的升压比[9]。相比于经典Boost直流变换器，两电平准Z源Boost直流变换器可实现很高的电压增益，因此在大升压比场景中该变换器被广泛应用[10]。直流变换器的数学模型在稳态性能、误差分析及控制策略研究等方面具有非常重要的作用[11],本文主要针对两电平准Z源Boost直流变换器进行数学建模。

1 拓扑结构与运行原理

两电平准Z源Boost直流变换器拓扑结构及运行状态如图1所示。图1(a)为该变换器的拓扑结构，该变换器的拓扑由2个电感，1个功率开关，2个二极管及3个电容组成。图中Uin为输入电压，iLl为电感L1电流，即输入电流；流过电感L2的电流为iL2；功率开关Q的电压应力(指功率开关Q关断时承受的电压)为UQ；二极管D1和D2的电压应力(指二极管关断时承受的电压)分别为UD1和UD2；UC1，UC2和UC3为电容C1，C2和C3两端的电压；Uo为输出电压，Io为负载电流。电感L2，电容C1和C2以及二极管D1组成准Z源结构，电感L1，功率开关Q，二极管D2和电容C3组成Boost直流变换器的拓扑结构，二者组合可得两电平准Z源Boost直流变换器的拓扑结构。设功率开关Q触发脉冲占空比为d，该变换器运行原理分析如下：

运行状态1。功率开关Q开通时(t0-t1)，二极管D1和D2关断，此时拓扑的运行状态如图1(b)所示。电感L1和L2处于充电状态，电容C1、C2和C3处于放电状态：电源Uin和电容C1对电感L1充电，电感电流iLl线性上升；电容C2对电感L2充电，电感电流iL2线性上升。负载能量由电容C3提供。设开关周期为Ts，则有t1-t0=dTs。

运行状态2。功率开关Q关断时(t1-t2)，二极管D1和D2开通，此时拓扑运行状态如图1(c)所示。电感L1和L2处于放电状态，电容C1、C2和C3处于充电状态，电源Uin和电感L1对电容C2充电，电感L2对电容C1充电，电源Uin、电感L1和L2对电容C3充电,负载能量由电源Uin、电感L1和L2提供，此时有t2-t1=(1-d)Ts。

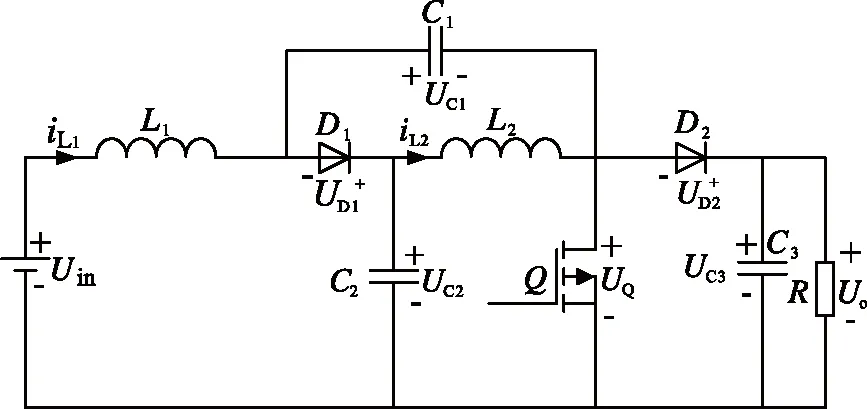
(a) 两电平准Z源Boost直流变换器拓扑结构

该变换器主要工作波形见图2。

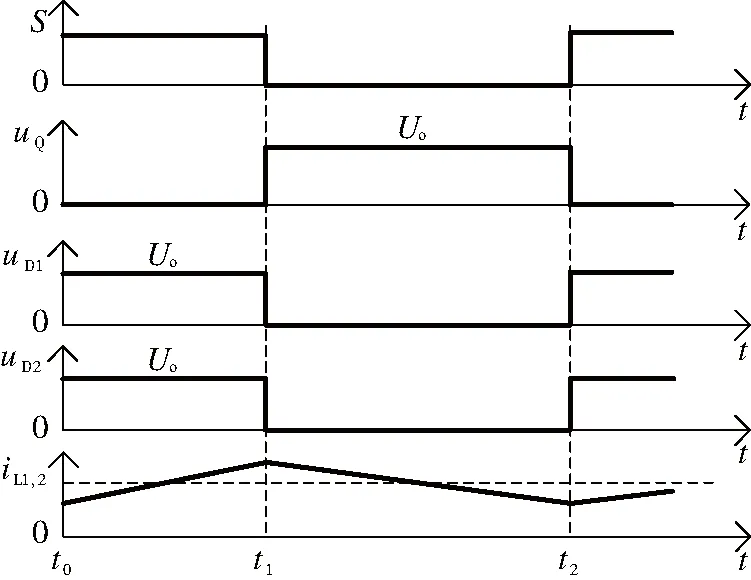
图2 直流变换器主要工作波形

2 变换器的数学模型及稳态分析

状态空间平均法是一种常用的直流变换器建模方法，该方法把储能元件作为状态变量，分别在不同开关状态下建立相应状态方程，通过将各状态方程以时间加权的形式进行叠加，进而得到直流变换器的数学模型。状态空间平均法要求不同开关状态下的状态方程阶数必须相同，并且每个状态变量都是独立的。

对于两电平准Z源升压直流变换器，当功率开关Q开通时(见图1(b))，储能元件不存在耦合关系，电感电流iL1(t)、iL2(t)，电容电压uC1(t)、uC2(t)和uC3(t)皆为独立的状态变量，可建立5阶状态方程；当功率开关Q关断时(见图1(c))，二极管D1和D2导通使电容C1，C2和C3构成仅容回路，电容电压uC3(t)=uC2(t)+uC1(t)，三者相互耦合，存在一个无效状态变量，只能建立4阶状态方程。由于不同开关状态下状态方程阶数不同，无法使用状态空间平均法建模。

考虑在电容C3支路串入寄生电阻r对电容电压进行解耦，如图3所示。当功率开关Q关断时，电容C1，C2和C3不再构成电容回路，uC1(t)、uC2(t)、uC3(t)皆为独立状态变量，电容电压实现解耦，此时可采用状态空间平均法建立两电平准Z源Boost直流变换器的平均状态模型和小信号状态模型。

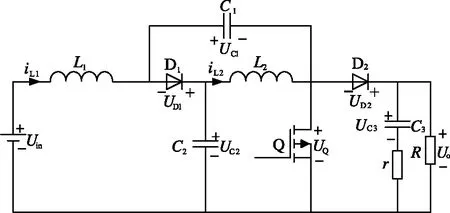
图3 引入串联电阻r的变换器拓扑结构

功率开关Q开通时，变换器运行状态如图1(b)所示，其状态方程如式(1)所示；功率开关Q关断时，变换器运行状态如图1(c)所示，其状态方程如式(2)所示。

根据状态空间平均法，由式(1)和式(2)可得变换器的平均状态模型,如式(3)所示。

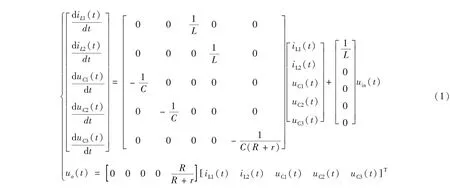
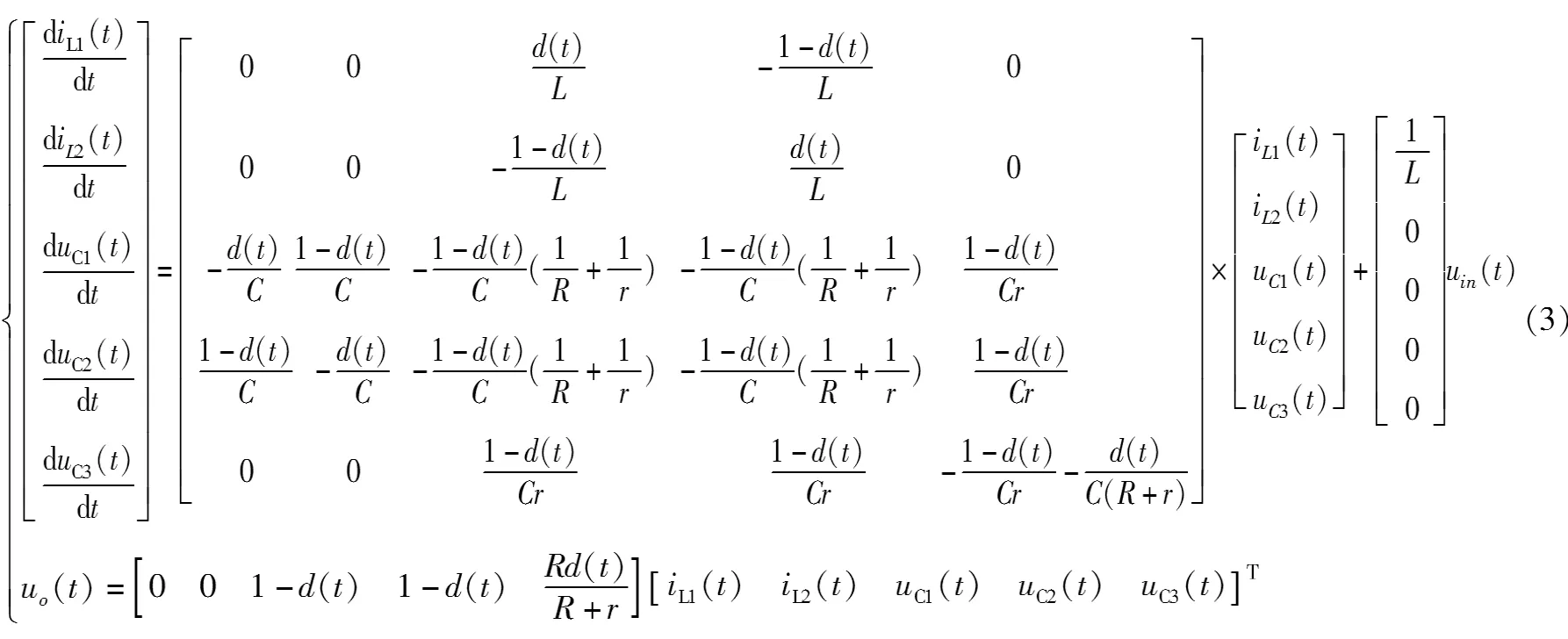
根据图1(c)，功率开关Q关断时，二极管D1和D2开通，此时有电容电压UC3=UC1+UC2，根据伏秒平衡原则，对电感L1与L2列出如下方程：

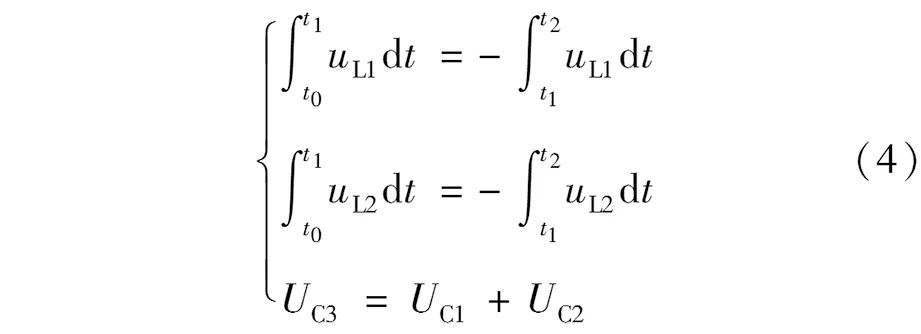
结合图1(b)和图1(c)，式(4)可化简为式(5)的形式。

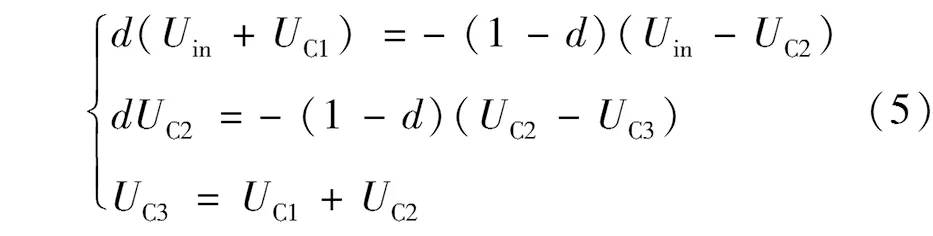
由式(5)可得：

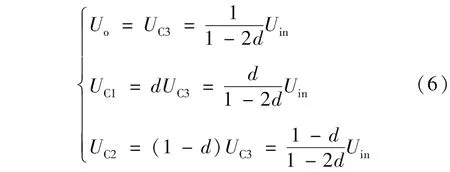
根据式(6)可知该变换器的电压增益为1/(1-2d)，由理想变换器的输入输出功率守恒可得输入电流Iin为

(7)

式中:Io—负载电流。

根据状态空间平均法由式(3)和式(8)可得变换器的小信号状态模型，如式(9)所示。

根据式(9)所示的变换器小信号状态模型，可分别求得从输出到输入的传递函数以及从输出到控制的传递函数，进而可设计变换器的控制策略并进行稳定性分析。

3 仿真验证与分析

根据图1(a)在MATLAB/SIMULINK中搭建该变换器的仿真模型(见图4)，并将其输出结果与数学模型计算结果进行对比(见图5)，进而验证所建数学模型的正确性。

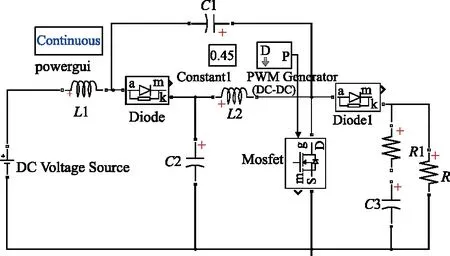
图4 两电平准Z源直流变换器仿真模型

相关仿真参数如下：输入电压Uin=40 V，占空比d=0.45，电感L1=L2=400 μH，电容C1=C2=C3=470 μF，寄生电阻r=0.01 Ω，负载电阻R=100 Ω。

由图5可知，变换器数学模型与仿真模型结果曲线的变化趋势基本一致，并且各稳态输出结果(输出电压、电感电流、电容电压)基本相同，证明了所建立数学模型的正确性和有效性。

(a)输出电压Uo

4 结论

本文对两电平准Z源Boost直流变换器建立了数学模型，包括平均状态模型与小信号状态模型。该变换器的电压增益为1/(1-2d)。从仿真结果可知，该变换器数学模型与仿真模型结果曲线的变化趋势基本一致，并且各稳态输出结果基本相同，证明了所建立数学模型的正确性和有效性。