基于卫星测高数据的海底地形反演研究
2021-05-16陈梅森
陈梅森
(广东省国土资源测绘院,广东 广州 510000)
0.引言
海底地形的研究一直是海洋测绘中的一个重要研究课题,海底地形作为海洋研究的基础性数据成果,能够为海底地质条件探索、海洋生态环境研究等提供基础数据信息,是全球海洋测绘工作的重要数据依据[1]。近年来,随着卫星测高技术的蓬勃发展,其分辨率及精确度得到了较大提升,并积累了大量的测高数据[2]。以卫星测高数据为基础,能够对大地水准面及重力异常进行精确反演,利用高精度的大地水准面和重力异常数据,可以实现区域海底地形的反演,且海底地形反演成果的精度也得到了大幅度提升[3]。
海底地形模型在海洋测绘工作中有着举足轻重的作用,卫星测高技术因其数据获取方便、数据量大以及分辨率高等优势,能够充分改善传统海底地形测绘方法的弊端,在海底地形测绘中的应用愈发成熟[4]。本次研究过程以卫星测高数据为数据源,对我国南海地区海底地形进行反演研究,利用垂线偏差法,对南海海域1′×1′重力异常格网模型进行精确构建,以卫星测高重力数据为基础,采用SAS 法对南海海域海底地形进行反演,将得到的海底地形模型与船测水深数据为基准,对海底地形反演模型进行分析,对基于SAS 法的海底地形模型精度进行综合验证。
1.研究区域
1.1 研究区概况
本次研究以我国南海海域为研究区域(如图1 所示)。我国南海海域处于太平洋西部,海洋运输交通条件极为便利,且南海海域海岛、海礁数量较多分布较广,有着较为广阔的大陆坡、深海盆地以及深海平原等[5],南海海底分布着较为广泛的海山和海沟、火山及地震等自然灾害较多,地形环境相对复杂,是国内外海洋领域专家学者的重点研究区域[6]。
图1 研究区域
1.2 数据源
本次研究以Geosat、ERS-1/2、Envisat、T/P、Jason-1/2、HY-2A 卫星测高数据为数据源,其中,Geosat 卫星测高数据选用由NOAA(美国国家海洋和大气管理局)发布的大地测量任务(GM)数据[7];ERS-1/2 以及Envisat 卫星测高数据选用由ESA(欧洲空间局)发布的GDR(地球物理数据)数据,ERS-1 主要包含ERM(轨道重复任务数据)数据以及GM 数据;T/P、Jason-1、Jason-2 卫星测高数据选用由CNES(法国空间中心)发布的GDR 数据,T/P 和Jason-1 测高数据主要包含卫星原始轨道数据以及变轨后数据;HY-2A 卫星测高数据选用由国家海洋局发布的GDR 数据。
2.数据预处理
2.1 共线处理
由于测高卫星的轨道具有一定程度的重复性,但由于卫星自身以及环境因素的影响,卫星轨道在每个运行周期期间都会有一定的偏差,从而使得海面高会随时间的变化而变化[9],为消除时间变化对海面高的影响,需将测高卫星多个运行周期的不同轨道通过一定方法拟合成同一条参考轨道,这个过程被称为共线处理。
2.2 确定参考轨道
在进行共线处理时,需获取测高卫星的参考轨道。本次研究采用经验法对各卫星的地面参考轨迹进行计算求解,对每条轨道的数据质量进行综合判断,选用数据量多且质量最高的测高卫星轨道作为参考轨道,经验法的优势在于不需要对正常点的位置参数进行精确求解,计算过程较为简单方便。各卫星参考轨迹(如图2 所示):

图2 各卫星地面参考轨迹
2.2.1 正常点海面高计算
在对卫星测高数据进行共线处理前,需计算正常点海面高,其方法为将卫星参考轨道上的数据点视作正常点,利用距离加权平均法进行求解[11]。本次研究以距离加权平均法为基础,分别对Geosat、ERS-1/2、Envisat、T/P、Jason-1/2、HY-2南海卫星测高数据进行共线处理,并将共线处理前后各卫星测高数据的自交叉点不符值进行对比分析,计算其均方根(如表1 所示)。分析可得,各卫星测高数据在进行共线处理后,其自交叉点不符值均呈下降趋势,故对研究区卫星测高数据进行共线处理,可在一定程度上降低海面时变因素对海面高的影响,从而提高卫星测高数据精度。

表1 共线处理成果分析

表2 交叉点平差成果分析
3.重力异常反演
在反演海底地形模型前,需对研究区范围内的海洋重力异常进行准确求解。
3.1 垂线偏差计算
垂线偏差实质是地球上一点沿重力方向与该点在椭球面上的法线所形成的夹角。各卫星测高数据在进行交叉点平差后所获得的数据成果为海面高数据,而垂线偏差计算的基础数据为大地水准面数据,故需要先计算各卫星测高数据的大地水准面高,如公式(1)所示:

式(1)中,N 为研究区范围内的大地水准面高;h 为在进行交叉点平差后的研究海域海面高;ζ 为稳定状态下的海面地形。
本次研究以EGM2008 重力场模型为参考模型,利用各卫星测高数据对南海海域1'×1'的垂线偏差进行求解计算,其子午圈、卯酉圈分量分布情况(如图3 所示):

图3 垂线偏差子午圈分量(左)、卯酉圈分量(右)
垂线偏差计算完成后需对其计算结果进行检校,将计算结果与现有模型进行对比分析,获取子午圈分量和卯酉圈分量分别与EGM2008 重力场模型进行综合对比(如表3 所示)。分析可得,计算结果与参考模型的子午圈分量、卯酉圈分量的RMS 相对较小,均低于1″,故求解的垂线偏差精度较高,可用于南海海域重力异常的反演。

表3 计算结果与模型差值统计
3.2 重力异常反演
本次研究采用移去—恢复的方法反演南海海域海洋重力异常,以EGM2008 重力场模型作为反演参考模型。在反演过程中,绝对值大于5″的残余垂线偏差主要分布在海岸线附近,故为了提高反演精度,需剔除大于5″的残余垂线偏差数据。为了获取研究区范围内的更高精度的重力异常数据,需要选取最佳的积分半径,经多方调研发现,30′是最佳积分半径。本次研究过程中以我国南海海域1'×1'格网残余垂线偏差为数据基础,对于绝对值大于5″的残余垂线偏差数据直接进行过滤处理,设定积分半径为30′,对南海海域1'×1'分辨率的重力异常进行反演(如图4 所示):

图4 南海重力异常
4.海底地形反演与结果分析
4.1 数据源
本次研究过程中的数据主要可分为三个方面,如下:
⑤ 低 LWR组(LWR≤0.248)患者 94例(36.6%),高LWR组 (LWR>0.248)患者163例(63.4%)。两组患者的各临床资料之间,差异无统计学意义。
(1)船测海深数据。船测海深数据为本次研究的数据基准,选用美国地球物理中心提供的高精度船测海深数据,船测轨迹(如图5 所示):
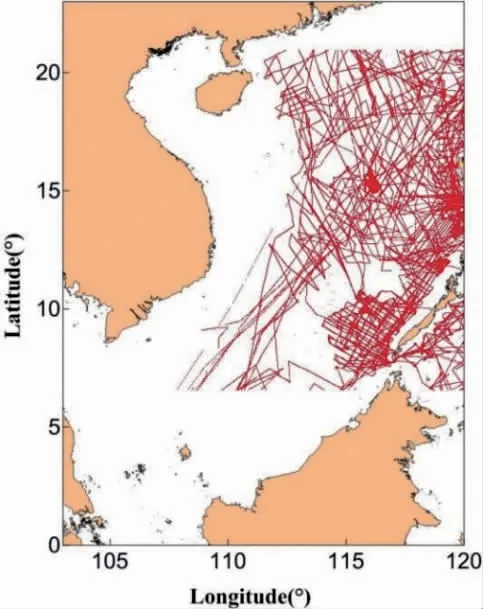
图5 船测水深数据分布
(2)海底地形模型数据。选取两种海底地形模型作为参考模型,分别为DTU10BAT 海底地形模型和ETOPO1 模型,分辨率均为1'×1'(如图6 所示):

图6 ETOPO1(上)、DTU10BAT(下)海底地形模型
(3)卫星测高重力异常数据。其是本次研究过程中基于各卫星测高数据反演的重力异常模型,分辨率为1'×1',相对船测重力异常精度为±4.5mgal。
4.2 SAS法反演海底地形
4.2.1 数据处理
SAS 法是以解析算法模型为基础,对海底地形进行反演研究,建立重力异常和水深之间的相对关系,由于重力异常和水深是非线性关系,故选用“移去—恢复”法来将其进行线性化。重力异常和水深其实质均为长波和短波的叠加,故首先需要对原始数据进行预处理,即分离原始数据的长短波,从而可得到长波参考海深以及残余短波分量,然后基于线性回归算法,对短波海深和重力异常之间的比例因子进行求解,然后构建短波海深模型,将短波海深模型与长波参考海深进行叠加,即可得到研究海域海底地形模型,具体步骤如下:
(1)基于SAS 法的海底地形反演,首先对ETOPO1 和DTU10BAT 海底地形模型进行滤波处理,设定滤波半径为160km,滤波后的成果为长波参考海深(如图7 所示):

图7 ETOPO1(上)、DTU10BAT(下)滤波后长波参考海深模型
(2)采用160km 波长的滤波器对船测海深数据以及格网化重力异常模型分别进行滤波处理,获取长波分量,然后将船测海深观测结果和格网化重力异常观测值与各自对应的长波分量进行作差,求解残余海深滤波和短波重力异常数据。
(3)反演海底地形模型的实质就是找出最佳的尺度因子S,多采用线性回归法,构建重力加速度(g)和尺度因子(S)之间的线性回归方程,回归方程的斜率即为尺度因子S。在实际应用过程中,首先将重力异常格网化规则点内插到船测海深非格网化离散点上,对船测点上的短波重力异常值进行计算求解,然后建立船测点上残余海深与短波重力异常间的线性回归方程,继而求解直线斜率(S)。本次研究过程中残余海深与重力异常的散点分布(如图8 所示),其最佳尺度因子为10.32m/mgal,将尺度因子与短波重力异常值进行乘积计算,其结果即为短波海底地形。

图8 海深与短波重力异常散点分布
(4)将模型长波参考海底地形与短波海底地形进行叠加处理,其结果即为研究区域海底地形模型。
4.2.2 精度评价与结果分析
在本次研究过程中,分别选用ETOPO1 和DTU10BAT 作为长波参考模型,其反演成果分别为SAS 海底地形模型1和SAS 海底地形模型2(如图9 所示):

图9 SAS 海底地形模型1(上)与SAS 海底地形模型2(下)
海底地形模型反演完成后,需对反演成果进行精度检校,以船测海深数据为真值,分别对SAS 模型1、SAS 模型2、ETOPO1 模型、DTU10BAT 模型进行精度检校。由于船测水深精度相对较高,可将船测水位视为海域实际水深,以船测数据点位为检核点,将各类模型数据内插到检核点中去,对各类海底地形模型中检核点水深进行计算求解,其结果与对应船测水深进行对比分析,研究各海底地形模型相对于船测水深模型的精度(如表4 所示):
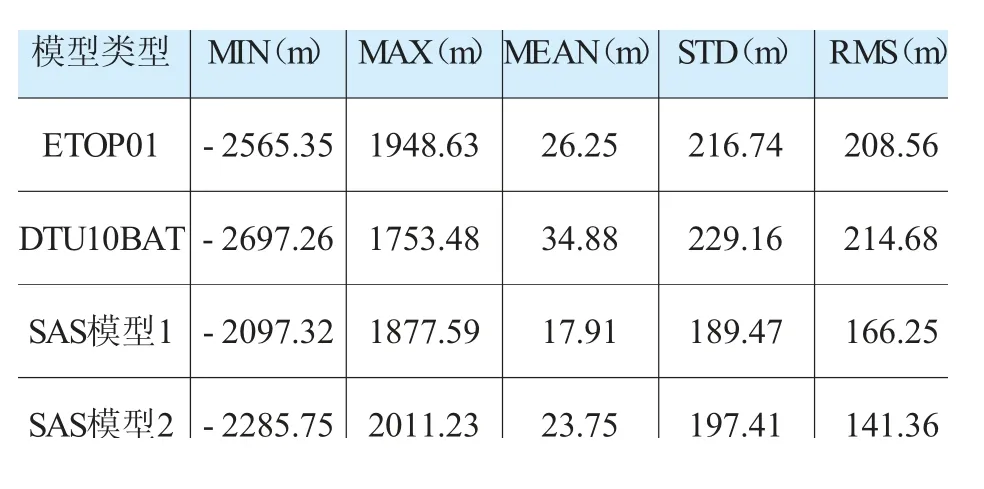
表4 各海底地形模型精度分析
由图9 可知,我国南海海域海底地形整体为西高东低,由于和大陆连接处的水深相对较浅,该区域海底地形相对较为平缓,随着水深的逐渐增大,出现较大陡坡,海底地形整体骤然降低,水深梯度的变化相对较为剧烈。分析表4 可得:ETOPO1 海底地形模型和DTU10BAT 海底地形模型的RMS分别为208m 和214m,基本一致,表明两种海底地形模型精度非常接近,但相对来说ETOPO1 海底地形模型精度略高于DTU10BAT 模型;SAS 海底地形模型1 精度相较SAS 海底地形模型2 精度略高,其主要原因是ETOPO1 长波参考海深模型自身精度高于DTU10BAT 长波参考海深模型,故以前者作为参考模型反演得到的SAS 海底地形模型1 精度同样高于SAS 模型2;从整体上而言,ETOPO 和DTU10BAT 海底地形模型的RMS 均大于200m,而SAS 模型1 和SAS 模型2 的RMS 分别为166.25m 和141.36m,故ETOPO1 和DTU10BAT海底地形模型的精度要低于SAS 模型,基于SAS 方法反演海底地形相对于现有模型精度提高50m 左右,具有较高的实用价值和参考意义。
5.结束语
本次研究过程以Geosat、ERS-1/2、Envisat、T/P、Jason-1/2、HY-2 卫星测高数据为数据基础,对我国南海海域的1'×1'重力异常进行反演计算,并结合ETOPO1、DTU10BAT 海底地形模型,采用SAS 法对我国南海海域1'×1'海底地形进行反演研究,与对应的船测水深数据进行对比分析,验证了SAS模型精度要高于现有模型,具有较高的实用性,为我国海底地形数据的获取,提供了较好的研究方向。
