长三角一体化战略背景下对上海港港口物流效率评价分析
——基于DEA-Malmquist模型
2021-05-15姚博鸿谭春兰
姚博鸿,谭春兰
(上海海洋大学 经济管理学院,上海201306)
引 言
上海一直以“中国之窗”著称,作为我国重要的港口城市之一,地理位置十分重要,地处我国海岸的中部,黄浦江与长江入海口的交汇处。境内的河道(湖泊)面积约500平方千米,河道长度2万多千米,河面积率在9%~10%之间。上海港不仅是我国海上运输通道的枢纽,也是我国重要的贸易港口之一[1]。作为我国贸易出口的重要口岸,上海港的集装箱、货物吞吐量一直稳居世界前列,这与上海港港口物流的发展是分不开的。同时,上海市政府为了增强上海港在国际航运市场的竞争力、促进经济的发展,也制定了一系列方针政策。2013年上海自贸区的设立,推动了港口物流的全面发展,同时在政策支持与配合下,实力显著提升。2018年,国家主席习近平提出将支持“长江三角洲区域一体化发展战略”上升为国家战略,上海港作为长三角的龙头港口,对长三角港口群的发展具有重要的引领作用。2019年12月1日中共中央、国务院印发的《长江三角洲区域一体化发展规划纲要》对今后长三角港航发展作出明确指示:“推进港航资源整合,优化港口布局,健全一体化发展机制,增强服务全国的能力,形成合理分工、相互协作的世界级港口群。”长三角一体化战略将成为推动港口物流发展的重大机遇。在这一背景下,加快上海港口物流建设,提高上海港口物流运行效率对推进长三角一体化战略的具有重要意义。上海港作为长江三角洲的前沿,具有空前的发展机遇[2]。2017年,上海港的货物吞吐量为75 051万吨,比上年增长6.9%,位居全国第二,仅次于宁波—舟山港。据统计(如图1所示),从2000年到2018年,上海港的货物吞吐量从量上看,虽然大体处于上升趋势,但从长期来看,其发展态势不容乐观,因为在整个研究期内上海港的货物吞吐量增速有所下降,甚至在个别年份处于负增长,增速波动幅度较大。由此可见,尽管在长三角一体化战略背景下,上海港口物流的发展态势良好,需求量增加,但仍然存在港口货物吞吐量不稳定、增速减缓等问题。因此,为了保证货物吞吐量的稳定增长,加快建设上海港成为国际航运中心,推动长三角一体化战略的有效实施仍需采取进一步措施。
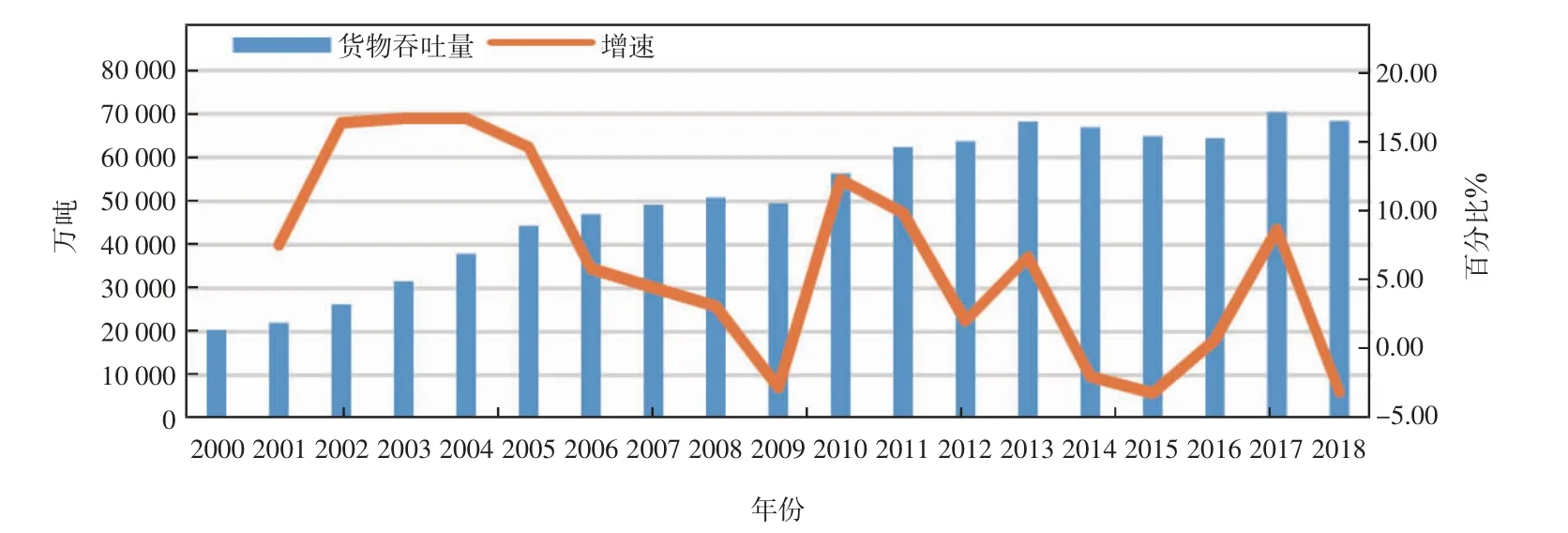
图1 2000—2018年上海货物吞吐量及增速
1 文献综述
数据包络分析方法(DEA)是由美国经济学家W.Copper等在1978年提出的,该方法以Pareto的边际效益和线性规划理论为基础,涉及运筹学、管理科学和数理经济学等多门学科,运用线性规划构建出一个非参数的线性生产前沿面,从而将数据包络起来,进而有效评价以多个投入和产出指标的决策单元相对有效性的一种综合效率分析法[2]。后期学者又对其进行补充和完善,Charnes等在1985年又提出了DEA的两个基本模型C2R和BC2模型,考虑了生产效率和边际生产效益问题,通过引入松弛变量s-、s+,将模型的分式规划问题等价变换为线性规划模型,使得规划结果同时达到“技术和规模有效性”的目标[3]。国外对港口物流效率评价研究较早。1986年国外学者Kim.M等就开始对港口效率值进行测度,应用单一指标对衡量港口效率进行衡量。此后学者陆续开始对相关领域展开研究[4]。
国内学者运用DEA模型在港口物流生产效率评价的研究也有丰富的成果。李谭(2012)通过利用DEA极效率模型,对港口物流的信息化评价进行实证分析。结果发现港口生产效率始终在较低水平徘徊,综合效率有待进一步提高[5]。戴金山(2013)选取我国主要集装箱港口为例,从全面绩效的角度出发,最后提出了,港口企业应制定新的经营战略,提高对市场敏感度,以应对以客户和服务为导向的新型服务模式的发展[6]。王丹平(2016)以盐田港为主要研究对象,从如何提高港口物流的管理效率的角度出发,通过构建计量经济学模型-DEA模型,对2006-2014年盐田港港口的生产绩效进行了深入研究。结果表明,这几年盐田港的综合效率值波动较大,内部结构需要进一步调整[7]。
当前国内学者运用DEA模型在港口物流的研究集中于对效率进行测度,而且多为静态效率值的测算,而对动态效率值及其效率影响因素的研究很少,仅有部分对效率影响因素的分析研究,员丽芬(2010)指出港口的区位优势、铁路与公路集疏运体系等因素对港口物流的生产效率具有重要的影响[8]。倪志敏等(2017)以广东省8个主要港口为例,结果发现,港口物流的信息化水平和陆运集疏运能力对提高港口物流效率值的贡献程度远大于腹地经济水平、贸易规模等外部因素对其的贡献,同时港口物流效率也受港口的区位优势、铁路与公路集疏运体系等内部因素的影响[9]。秦雯(2019)以珠海港口为例,最后提出珠海港港口物流的生产绩效与相关的资源利用率和贸易规模具有密切关系。本文主要通过以上海港港口为例,选取2000—2018年上海统计年鉴数据,在对其静态效率值测算值后,结合Malmquist指数分析法对其动态效率值(全要素生产率)进行综合分析,补充了以往研究的不足,以期为我国港口物流评价相关的研究提供借鉴[10]。
2 研究方法和评价指标
2.1 研究方法
为了深入研究上海港口物流的生产效率,运用数据包络分析(DEA)方法构建DEAMalmquist模型对上海港口生产效率进行测算,以考察上海港口物流的运行效率,该方法运用投入—产出模型作为研究目标,通过从生产前沿面上的技术有效性和规模有效性两个维度来对测算出的运行效率值进行评价,进而衡量港口物流业的运行效率。DEA模型主要模型和Malmquist指数分析法介绍如下:
(1)DEA模型
数据包络分析法(DEA)是运用线性规划构建出一个非参数的线性生产前沿面,从而将数据包络起来,进而有效评价以多个投入和产出指标的决策单元(DMU)相对有效性的一种综合效率分析法[11]。
假设有n个决策单元(DMU),X1、X2、X3,…,Xt是每个决策单元DMU的投入项,X1、X2、X3,…,Xs是每个决策单元DMU的产出项,即DMU满足以下式子:
DMUi=(1≤i≤n),其中Xi、Yi分别是决策单元DMU的多指标投入矩阵和多指标产出矩阵,且分别满足:Xi={x1i,x2i,…,xtiT},Yi={y1i,y2i,…,ysiT}(xti和ysi分别表示第i个决策单元的投入量和产出量)。
再设V={v1,v2,…,vtT}、U={u1,u2,…,usT},(U、V≥0)分别为投入和产出向量的权向量,则每个决策单元DMU的效率评价指数可以表示为:总产出向量和总投入向量的比值,即:
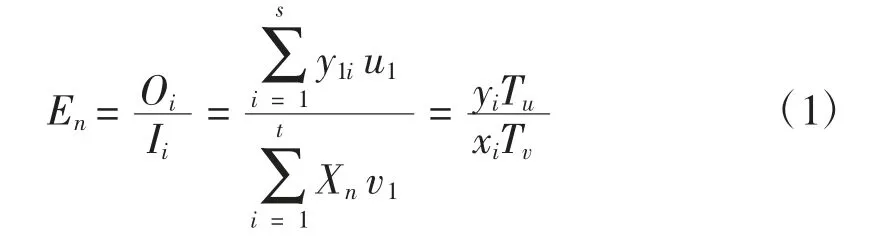
由(1)式可知,通过对各个向量指标的权重进行调整,必然能得到最优的投入产出比,但是这样很容易造成企业一味地追求投入产出,忽略对其他因素的考虑。因此,为了改进这一缺陷,A.Charnes与W.Cooper提出了C2R和BC2模型,考虑了生产效率和边际生产效益问题,通过引入松弛变量s-、s+,将模型的分式规划问题等价变换为线性规划模型,使得规划结果同时达到“技术和规模有效性”的目标[12]。
C2R模型是以规模报酬不变的假设为条件,只能用于测算决策单元(DMU)的综合技术效率(crste)。规模报酬不变下,DEA的C2R模型表示为:对决策单元(X0Y0),求下列极值问题:

式(2)中求出的ω值即为决策单元(X0Y0)的综合技术效率值(TE),λi(i=1,2,3…n)为对偶变量,s-,s+为松弛变量,在(2)式的基础上再加一个条件,即得到BC2模型:
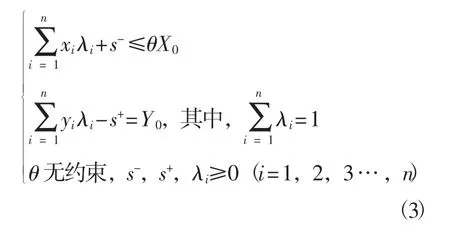
式(3)中求出的θ值即为决策单元(X0Y0)的纯技术效率值(PTE),由于BC2模型中决策单元的规模报酬是可变的,因此可将C2R模型得出的综合技术效率值(TE)分解为纯技术效率(PTE)和规模效率(SE),再由规模效率(SE)与纯技术效率(PTE)的乘积为综合技术效率(TE),可求得规模效率(SE),即SE=TE/PTE。最后再根据θ,ω,s-,s+值的不同情况可以得出以下结果:若θ,ω=1,s-,s+=0,则决策单元(X0Y0)是位于效率前沿面上的点,该决策单元(X0Y0)DEA有效;若θ,ω=1但是s-或s+不为0,那么该决策单元(X0Y0)是DEA弱有效;若θ,ω<1,则该决策单元(X0Y0)是DEA无效,DEA无效的决策单元可通过测算出的s-,s+的值进而对无效决策单元的投入和产出进行调整(s-,s+分别表示决策单元的产出不足数和投入冗余数)[13]。
(2)Malmquist指数分析法
为更加深入地对上海港港口近些年的生产效率的变化情况进行分析,本研究在对上海港港口静态效率值分析之后,同时结合Malmquist指数分析法对上海港口近19年数据进行了动态效率的分析。Malmquist指数分析法也是基于DEA模型对效率值进行测算的一种方法,只是Malmquist指数分析法考虑了时间变化的因素,侧重于对企业全要素生产率动态变化的分析[16]。相关动态效率指数值主要有五个,分别是表示技术效率变化的指数(Effch);表示技术进步变化的指数(Techch);表示纯技术效率变化的指数(Pech);表示规模效率变化的指数(Sech)和全要素生产率指数(MI)。通过分析这些指数值的大小能反映出相应的不同的状态[17]。其中全要素生产率指数MI>1,表示MI处于增长阶段;MI<1,表示MI处于下降阶段;MI=1,表示MI处于不变状态。表示技术效率变化的指数Sech常用于衡量在相同投入的前提下,最终的实际产出与预期最大产出之比;表示技术进步变化的指数Effch大于1时,表明DMU的技术水平处于较高阶段,而Effch小于1时则表示技术水平存在不足[18]。表示技术进步的指数Pech,反映了技术水平的提高对产出增长的促进作用。若Pech>1,则表明决策单元内出现技术进步。上述效率指数之间的关系可用公式表示为:MI=Effch*Techch;Effch=Pech*Sech,即MI=Effch*Techch*Pech*Sech。
鉴于综合效率值(Crste)、技术效率(Vrste)、规模效率(Scale)值反映了在一定时点上的效率值,即从静态的角度对效率的测算,而Malmquist指数所包含的效率值考虑了时间变化的因素,即从动态的角度对效率的测算。因此,本文为了便于分析,将上述前者效率值定义为静态效率值,后者定义为动态效率值。
2.2 评价指标与数据
2.2.1 评价指标的确定
由于港口物流的发展,这一概念具有复杂性、笼统性的特征,国内至今对此研究还未形成一套统一的方法和衡量指标。目前,能够反映出港口物流发展水平的指标主要有:港口货物吞吐量、货物运输量、集装箱吞吐量以及港口航线等相关指标。因此本文从指标的实用性和代表性的角度,主要选取港口货物吞吐量和集装箱吞吐量作为产出指标,将码头长度、码头泊位总数作为投入指标,具体如下表1所示。
(1)输入指标
码头长度和码头泊位数。港口码头长度和码头泊位数是反映港口物流供给能力的重要因素,是港口所在区域范围内必备的基础条件之一。当前很多大型港口为了提高装载效率和降低运输成本,开始朝船舶大型化和专业化方向发展,因此对码头泊位数及码头长度等基础设施提出了更高的要求。港口的码头长度和泊位数在一定程度上决定着停靠船舶的数量和级别,是衡量港口码头大小的重要标准。因此本文选取这两个数据作为输入指标。
(2)输出指标
港口货物吞吐量和集装箱吞吐量。货物吞吐量和集装箱吞吐量是反映港口物流需求规模的重要指标。吞吐量的大小直接体现了港口所能容纳的货物周转量。吞吐量越大,港口的需求规模也就越大,所获得的经济收益也就越高,是评估港口物流效益水平高低的重要指标。集装箱运输是港口物流现代化的产物,集装箱吞吐量是衡量港口国际化水平的重要标准。因此本文选取以上两种数据作为输出指标。

表1 评价指标
2.2.2 数据指标的收集和整理
本文通过查询上海统计年鉴2000-2018年的数据以及其他相关信息,收集到相关数据,具体投入产出数据如下表2:
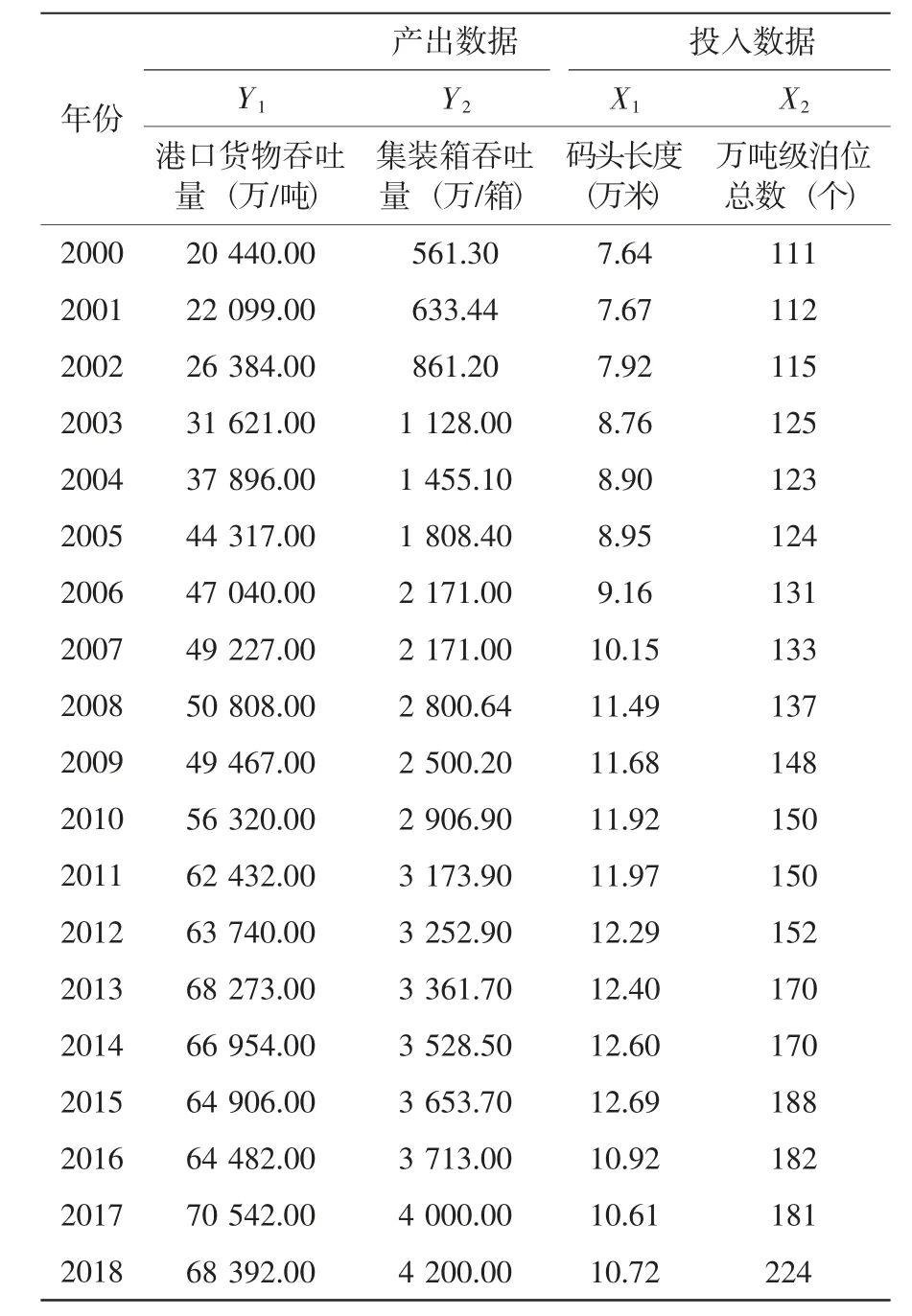
表2 输入和输出数据
3 结果分析
该文采用DEAP2.1软件,对上海港口物流发展效率进行计算,结果如下图表所示,其中纯技术效率评价的是在一定投入下能达到的产出能力,规模效率反映了上海港口19年来物流业的发展规模。投入和产出的原始数据均来源于2000—2018年《上海统计年鉴》计算具体结果如表3所示。
为了便于分析,将上述表中的静态效率值,汇成散点图,如图2所示。
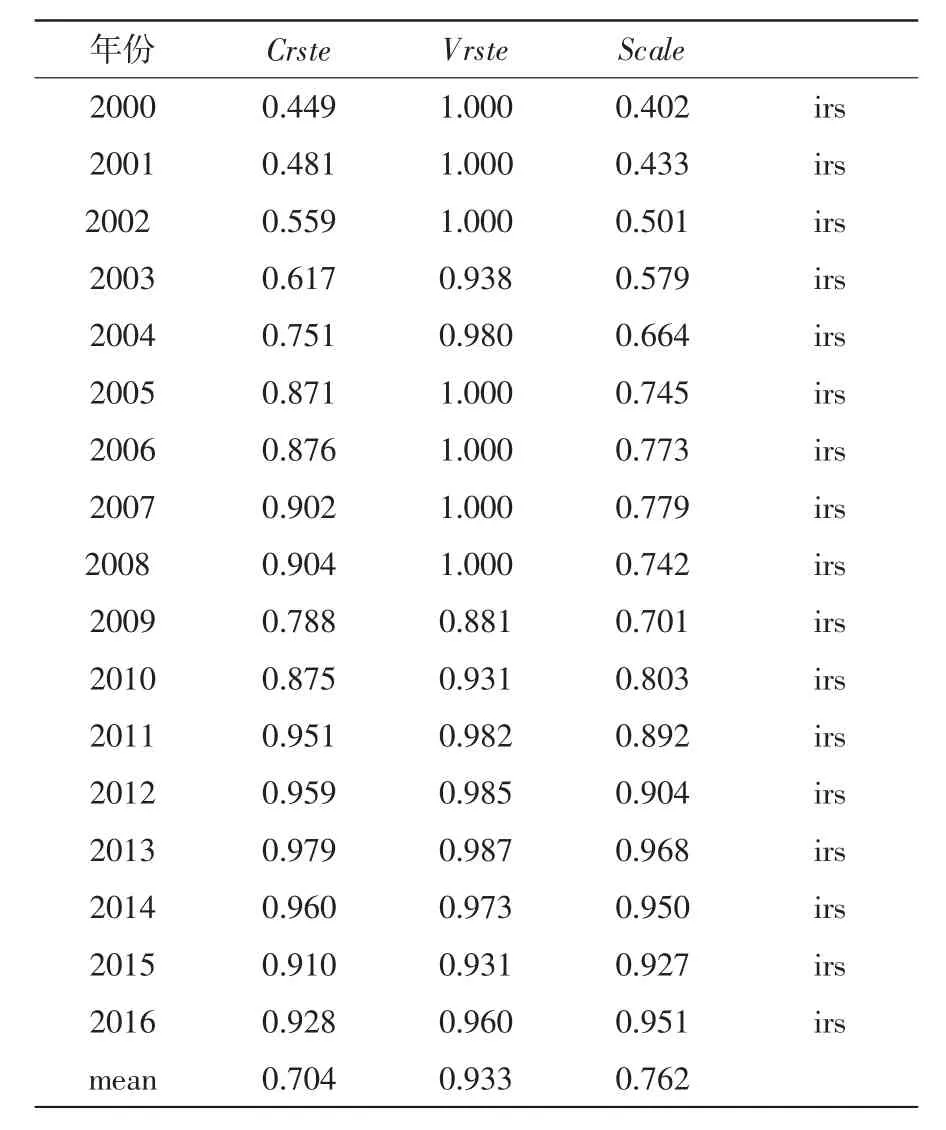
表3 2000—2018年上海港口物流技术的静态效率值
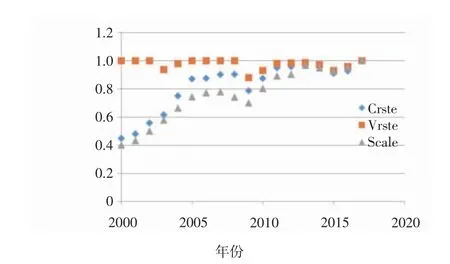
图2 静态效率值
根据表3和图2可得:(1)对综合技术效率值分析。通过观察表中数据和散点图的大致走势,我们可以看出,上海港口物流的综合技术效率从2000—2017年一直处于增长的趋势,大体可以分为两个阶段:第一个阶段为2005之前,在这一阶段具有的显著特点,综合技术效率值处于快速增长时期,平均增长率达6%。主要是入世以来国内经济处于高速增长,上海港口在良好的国内环境下,通过对技术的不断更新,港口物流效率不断加大。第二个阶段为2005之后,在这一时期上海港口物流综合技术效率处于缓慢增长的阶段,平均增长率约为2%。而且一直处于0.9~1之间,说明近些年上海港口物流效率呈现逐年递增但是仍未处于DEA有效状态,还不是最优。
(2)对纯技术效率值分析。通过观察我们可以看出,2009年以前,上海港口物流的纯技术效率值基本均为1,说明在这一时期上海港口物流的技术效率是处于最优状态,即达到了在同等投入的前提下,产出的最大化。但是2009年之后,上海港口物流的纯技术效率值有所下降,虽然大都处于0.9~1之间,总体还算稳定,但是纯技术效率除了2017、2018年份达到最优外,其余年份效率值都没有达到有效。由此可见长三角一体化战略对上海港口物流发展确有一定推动作用,但是为了保证上海港口物流效率的长期最优,上海港口在技术优化投入方面仍需进一步强化。
(3)对规模效率值分析。在2017和2018年上海港口物流的规模效率值为1,表示港口物流的规模效率值处于有效状态,反映了投入产出比达到了最优,企业投入规模符合合理性的标准。其次是2012—2016年上海港口物流的规模效率值在0.9~1之间,说明上海规模效率整体还比较平稳,但是为了保证规模效率值处于长期最优和稳定,未来仍需在完善港口物流基础设施方面继续努力,努力构建出一个合理有效的长期增长机制。
(4)对规模报酬的分析。在整个研究期间上海港口物流的规模报酬始终保持着递增的状态,表明各个年份均达到了最佳规模,表明在其他条件保持不变的情况下,每增加一单的投入,所收获的产出增加值大于投入的增加值,因此可以在现有的基础上再扩大经营规模。
在此基础上,再将上海港口作为独立决策单元,对2000—2018年上海港口物流技术的Malmquist指数值进行测算,得出的Malmquist指数及其相关效率指数如下表4。
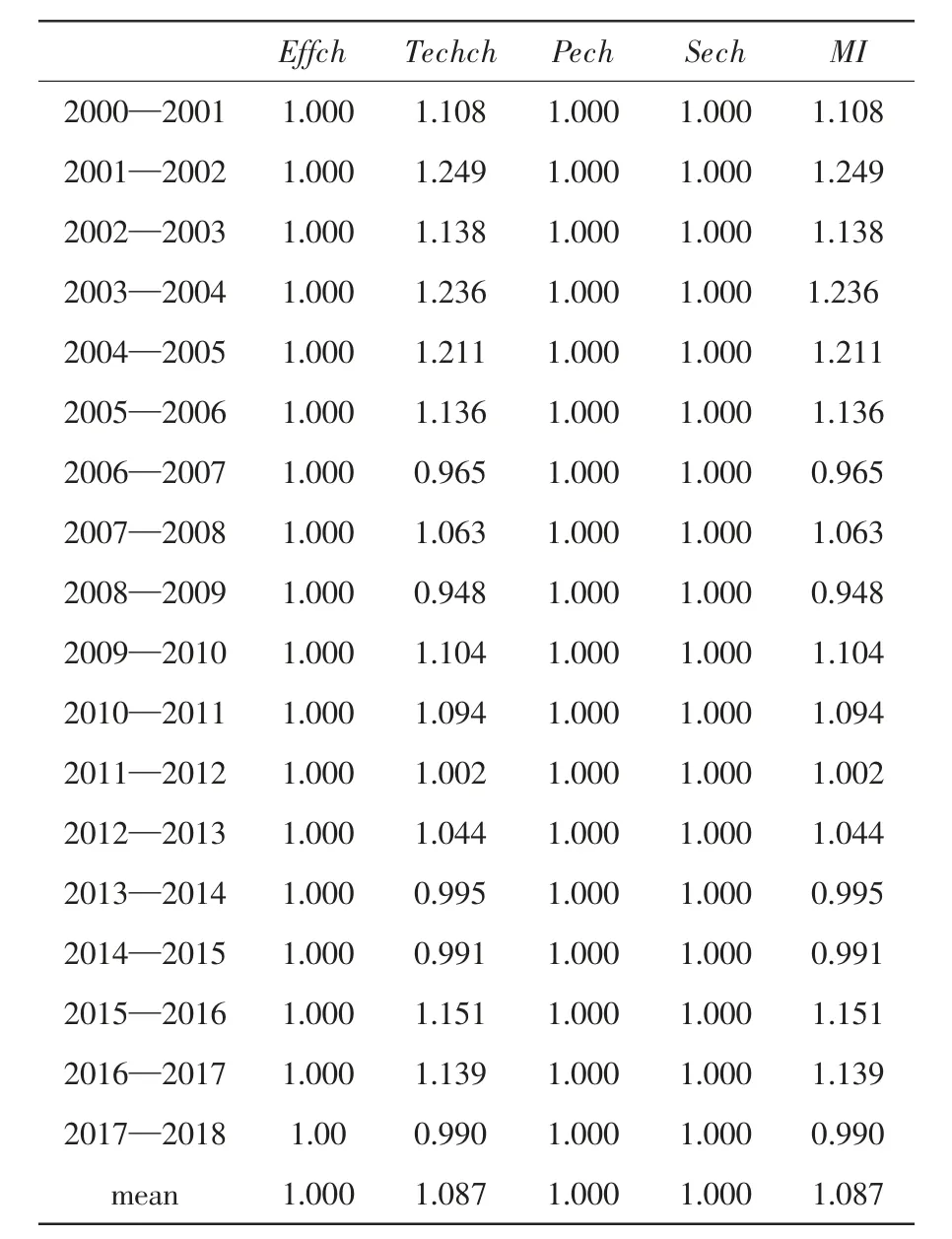
表4 2000—2018年上海港口物流技术的动态效率Malmquist指数
将上述测算的效率值,汇成条形图,如下图所示。
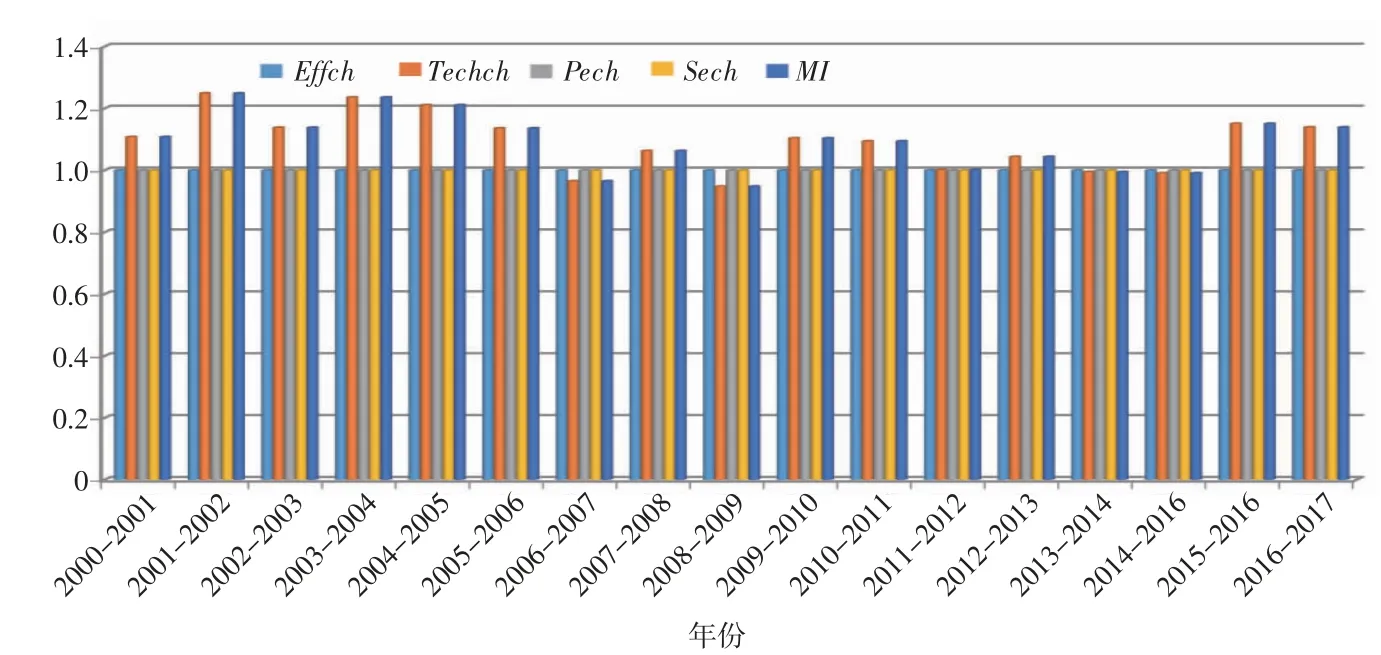
图3 动态效率Mulmquist指数
通过观察表4动态效率Mulmquist指数,可以看出,近些年上海港口的Malmquist指数综合均值为1.089,说明上海港口的全要素生产率总体呈上升趋势,但是仔细分析我们可以发现相近的两年间的Malmquist指数值并非一直处于上升的趋势,动态效率很不稳定。进一步观察图3中MI指数变化,发现其具有明显的阶段性特征,大致可分为两个阶段:第一阶段2000—2006年,在这一时期内的全要素生产率总体呈现显著上升的趋势,平均上升幅度为17.9%,总体效率值指数较高,而且始终有MI>1。第二阶段2007—2017年,该阶段MI值一直处于不稳定状态,而且普遍较低。平均增长率仅为4.5%,甚至有个别年份出现全要素生产率值小于1的情况,主要是2007、2009、2014、2015这四年的MI值,分别为0.965、0.948、0.995、0.991。主要原因是技术效率发生作用,劳动力要素投入趋于饱和、自身技术进步下降等导致了全要素生产率的下降。从总体来看,这一阶段上海港口的全要素生产率一直在0.9~1.1上下波动,虽有所增长,但是存在个别年份的全要素生产率的下降,整体来看并不是很稳定。
4 结论与建议
本文通过利用DEA模型同时结合Mulmquist指数对上海港的物流生产效率的评价进行实证研究。根据分析的结果可以看出:
(1)研究期间内上海港口物流静态效率值逐年升高,但很少达到DEA有效状态。以综合技术效率值分析为例,在整个研究期间上海港口物流的综合技术效率均值相对较高,在0.7以上,而且呈现明显的“阶梯式”增长走势。通过观察测算结果,可以看出上海港口物流综合技术效率值经历了先明显上升后缓慢增长的“阶梯形”轨迹。原因是:入世以来,我国宏观经济不断向好,在这期间上海港口经历了经营方式和体制与国际逐步接轨,技术日益更新,规模也在不断扩大。因此,综合效率值一直处于快速增长阶段。但是,伴随着企业规模的不断扩大以及设备更新和技术发展的时滞性特征,上海港口物流综合技术效率值的增长逐渐降低。通过进一步与规模效率值的对比,可以发现,上海港口物流总体效率和规模效率的变化具有一致性,从而说明上海港口物流规模效率的变化是引起上海港口综合技术效率值变化的主要原因。
(2)研究期间内上海港口物流动态效率值很不稳定,甚至有所下降。通过观察Malmquist指数数据我们可以看出,在研究期间内上海港口物流的动态率值的变化完全取决于技术进步的变化。首先看2000-2006年期间,上海港口物流的动态效率值总体呈上升状态,通过结合静态效率值:不考虑规模收益时的技术效率和考虑规模收益时的技术效率值数据,发现在这一期间的这两种效率值的变化也是呈上升趋势的。同时发现它的动态效率值(技术进步变化值)和全要素生产率也具有完全一致性;再看2006年之后动态效率值一直处于不稳定状态,有下降趋势但是基本均在0.9~1上下浮动,结合静态效率值不考虑规模收益时的技术效率和考虑规模收益时的技术效率值数据,仍然具有类似特点。可知技术效率和技术进步变化是引起全要素生产率的变化的主要原因。
综合来看,近些年上海港的物流绩效虽不断提高,但是上海港在2017年之前的综合技术效率值全都小于1,均尚未达到DEA有效状态,并且上海港的动态效率值并不是很稳定。因此,目前上海港为加快国际航运中心建设,推动长三角一体化战略的有效实施仍需要进一步改进和完善。
根据上述分析本文提出以下几点改进建议:
(1)提升港口规模化水平,加大对基础设施建设的投入。根据前文分析得出港口物流规模效率的变化是引起上海港口综合技术效率值变化的主要原因。因此,上海港可以从优化港口企业规模出发,在不断推进港口码头朝着深水化、专业化和规模化方向发展的同时注重调整经营规模、提高货运能力,完善集疏运体系进一步提高上海港口综合技术效率。
(2)加强港口的软环境建设。注重对员工技术方面的培训和相关高素质专业人才的引入,同时提高设备更新率以及先进物流技术的应用,从企业管理的战略出发进一步改善港口物流管理方式以提高港口物流的技术效率。
(3)整合港口资源,进一步提高港口专业化水平。上海港在注重自身发展的同时可以通过将周边的一些物流企业和物流资源进行整合,剔除冗杂的物流环节,努力为客户打造一个更加全面和专业化的供应链体系,通过提供一体化物流服务,以提高港口物流产业链的高效运转速率。
(4)依托国家政策,发挥地区优势。上海港要立足高位,在“长三角一体化战略”以及临港新片区的国家战略中,充分发挥地区优势,提升上海航运高端服务功能和科技创新策划能力,进行合理的港口物流规划,巩固龙头港口的地位,提高港口物流辐射能力,推动上海品牌和管理模式的全面输出,为长三角高质量发展和参与国际竞争提供服务。
