基于RBF 神经网络的压电位移台迟滞非线性建模研究∗

周 哲杨晓京

(昆明理工大学机电工程学院，云南 昆明650500)

近年来，随着超精密制造业的发展，微纳米驱动定位技术受到了广泛的重视[1]。 压电陶瓷作动器具有能量密度大、响应速度快、精度高等优点，被作为理想的微位移驱动器，在超精密加工，微机电系统，纳米生物工程，航空航天等领域得到了广泛的应用[2]。 但由于压电陶瓷材料其本身所固有的迟滞非线性特性对其定位精度的影响，使得由压电陶瓷作动器驱动的微位移平台的应用和推广受到了极大的限制[3]。 因此，消除压电陶瓷的迟滞非线性对其定位精度的影响，以实现高精度的定位，是目前研究的关键和热点问题[4-5]。

针对压电陶瓷位移台的迟滞非线性对压电微定位台定位精度的影响这一问题，目前的主要研究方向是通过建立各种迟滞非线性的系统数学模型，来模拟压电陶瓷输入电压和位移之间的迟滞关系[6]。当前国内外比较常见的有Preisach 模型[7]、Prandtl-Islinksii 模型[8-9]、Jiles-Atherton 模型[10]、Bouc-Wen模型[11]等。 但由于他们的逼近精度受到模型迟滞单元的描述能力的影响，在大功率的输入条件下，建立的动态迟滞非线性模型稳健性会变差[12]。 近年来，越来越多的学者选择将神经网络运用到压电作动器的迟滞建模中。 Tai N 等人基于Kuhnen 的动态迟滞结构，利用迟滞算子对输入的映射关系进行转换，建立了压电陶瓷的迟滞神经网络模型[13]，张新良[14]和赵新龙[15]利用扩展迟滞输入空间的方法，建立了具有速率依赖性的迟滞算子的神经网络模型。

本文采用基于play 算子的改进的PI 模型和RBF神经网络模型来构建压电陶瓷微位移台的迟滞模型。通过与实验结果的对比表明，该模型能够以较小的误差准确有效的描述压电陶瓷的迟滞特性，而且具有较好的频率泛化能力，易于工程实现。

1 迟滞模型的建立

当压电陶瓷位移台的输入电压频率变化较大时，其输入和输出关系变化较大，表现出和输入电压频率相关的迟滞特性，如下图1 所示。 径向基函数神经网络(Radial Basis Function，RBF)结构简单、收敛速度快、是一种具有三层结构的前向神经网络，对非线性网络具有一致逼近的性能，因此用来辨识迟滞非线性特性具有独特的优势，可以减少传统模型因受限于单元描述能力而造成的误差。

图1 压电陶瓷位移台的率相关特性

1.1 迟滞算子

由于前向神经网络只能逼近一对一的映射关系，而压电陶瓷的迟滞特性表明，在不同时刻相同的输入下，存在不同的迟滞输出与之对应，即为多对一的映射关系。 为了将前向神经网络用于多值映射的辨识，因此需要引入一个迟滞算子来拓展神经网络的输入空间，将迟滞过程中多对一的映射转化为一对一的映射关系，如图2。

本文选用PI 模型的play 算子来构造神经网络的迟滞算子，如图3。

图2 拓展输入空间

图3 play 算子示意图

单个play 算子的数学表达式如下:

式中:r为play 算子的阈值；x(k)为算子输入；y(k)为算子输出。 由于电压值恒为正，因此只用到完整play 算子的第一象限部分。

在升压过程中，当x(k)≤r时，算子输出y(k)保持为零；当r≤x(k)≤xmax时，y(k)的输出为x(k)-r；在降压过程中，当输入电压从xmax降到xmax-2r的过程中，y(k)的输出保持为xmax-r；在输入电压从xmax-2r降到零的过程中，迟滞输出为y(k)＝x(k)＋r。

因为Play 算子具有和压电陶瓷相似的迟滞现象，将多个Play 算子与各自的权值相乘之后叠加，即可得到模拟压电陶瓷的PI 迟滞算子模型，其数学表达式为

式中:n为叠加的Play 算子的个数；Y(k)为k时刻PI 迟滞算子的输出；ωi为第i个Play 算子的权值；ri为第i个算子的阈值。

可将上式写为向量形式:

1.2 RBF 神经网络

径向基函数神经网络(Radial Basis Function，RBF)结构简单、收敛速度快、是一种具有三层结构的前向神经网络，对非线性网络具有一致逼近的性能，因此用来辨识迟滞非线性特性具有独特的优势，可以减少传统模型因受限于单元描述能力而造成的误差。

在径向基(RBF)网络中，输入层把输入向量输到隐含层，隐含层神经元一般由径向基函数组成，而输出层则根据线性最优策略进行调整。 隐含层的激励函数会对输入量产生局部调整，距离基函数中心区域越近，其调整响应就越剧烈，所以RBF 神经网络具有强大的逼近能力。 其结构如图4 所示。

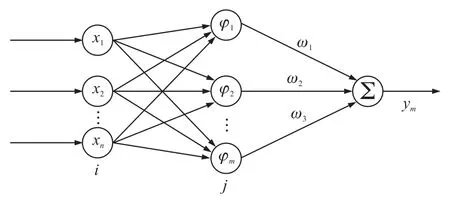
图4 RBF 神经网络结构

由于高斯函数的差值结果和网络结构最为接近，本文选取高斯函数作为RBF 神经网络的基函数，其学习过程如下:

确定中心以后，高斯基函数的标准差按照以下公式选取:

式中:dmax为所选取中心之间的最大距离，n，m为输入层，隐含层个数；神经网络的输入为x＝[x1，x2，…xn]，φj为隐含层第j个神经元的输出，如下式:

上式中，cj＝[cj1，cj2，…，cjn]为隐含层第j个神经元中心点的向量值。 输出层的权值为ω＝[ω1，ω2，…，ωm]T，由上可得，RBF 网络的输出为:

本文采用均方根误差(Root mean square error，RMSE)和相对误差(Relative error，RE)来作为检测误差的标准，描述所建立的仿真模型的拟合效果。计算公式如下:

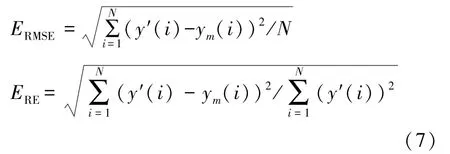
式中:N为采集样本数据的个数；y′(i)为采集到的压电陶瓷作动器的实际位移输出；ym(i)为建立的RBF 神经网络模型的输出，由式(6)得到。

2 仿真结果和实验验证

采用如图5 所示的实验设备进行压电位移数据的采集。 其中压电微微位移定位台采用哈尔滨芯明天公司生产的三维压电定位台XP-611.XYZ，其内部装有lvdt 位移传感器以测量定位台的位移，其分辨率可达0.02 μm。 压电陶瓷控制器采用XE-500/501D 系列控制器，由功率放大器、传感器控制模块和显示接口模块组成。 实验过程如下:首先由计算机发出信号，经控制器进行D/A 转换变为模拟信号，经过控制器内部的功率放大模块放大，作用于微位移台上，产生位移并实时检测传回计算机控制系统。

图5 实验装置

本文使用输入信号频率为2 Hz，幅值为70 V 时的正弦电压，输入电压信号为U＝30sin(4πt-/π/2)＋40，确定相应的迟滞算子信号以及输出信号，通过使用MATLAB 神经网络工具箱，调用newrb 函数构建标准的三层RBF 神经网络。 隐含层使用高斯径向基函数，输出层为隐含层输出的线性加权和，如式(6)所示。

为了验证模型的率相关性，将频率为10 Hz，电压幅值为70 V 时的正弦电压作为输入信号输入到建立的RBF 神经网络仿真模型中，得到10 Hz 时输出的仿真位移数据，并与频率为10 Hz 时的压电陶瓷作动器输入输出数据进行比较，计算一个周期内的误差，结果如图6。

从图6(a)可以看出，RBF 神经网络模型的仿真曲线和压电陶瓷位移台的实验迟滞曲线基本上重合。由图6(b)中的误差曲线可以得到，在频率为10 Hz时，仿真模型输出位移的最大误差为0.399 0 μm，计算可得模型的平均误差为0.259 4 μm，均方根误差为0.138 3 μm，相对误差为0.95%，说明构建的RBF 神经网络仿真模型能够比较精确的描述压电陶瓷微定位台的迟滞非线性特性。

为了更好的验证压电陶瓷的迟滞现象的率相关性，使模型具有更优的频率泛化能力，本文使用电压幅值为70 V，频率分别为30 Hz，60 Hz，90 Hz 的正弦信号作为输入信号，输入至构建的RBF 神经网络仿真模型中，得到相应的仿真输出位移，并与实验所采集的位移数据进行比较，得到如图7～图9 所示的迟滞曲线和误差曲线:

图6 频率为10 Hz 时，仿真结果与实验数据对比

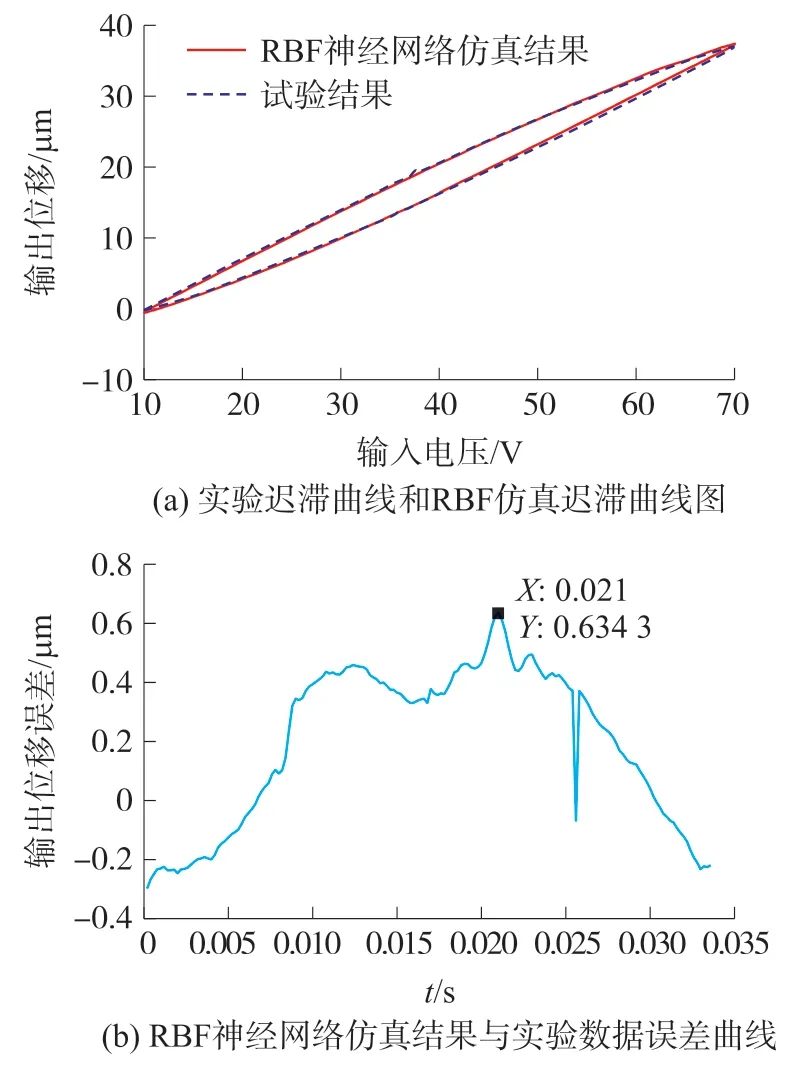
图7 频率为30 Hz 时，仿真结果与实验数据对比

图8 频率为60 Hz 时，仿真结果与实验数据对比

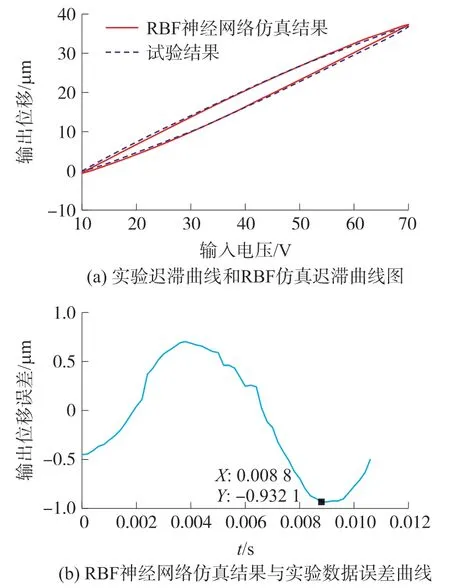
图9 频率为90 Hz 时，仿真结果与实验数据对比

由于误差相对于整体位移来说量级过小，在迟滞曲线中无法直接观测出明显差别，可从误差曲线中分析得到，在输入电压频率从30 Hz 升至90 Hz时，相对与10 Hz 时的仿真结果而言，最大误差，均方根误差和相对误差均有不同程度的小范围上升，这是由于压电陶瓷自身的动态特性造成的。 分析整理图6～图9，可列出表1。 由表1 可以看出，随着输入电压频率的升高，RBF 神经网络模型输出的平均位移误差出现持续的减小趋势，说明RBF 神经网络模型在搜索逼近过程中迭代均匀，并未陷入局部最优。 由图6～图9 和表1 可以看出，在输入电压频率为10 Hz～ 90 Hz 时，仿真模型的最大误差仅为0.399 0 μm～0.932 1 μm，均方根误差仅为0.259 4 μm～0.565 2 μm，相对误差为0.95%～2.48%，表明本文构建的RBF 神经网络模型在10 Hz 至90 Hz 的输入电压范围内，具有较好的频率泛化能力，能够在整体上以较高的精度拟合压电陶瓷的迟滞非线性特性。

表1 RBF 神经网络模型误差分析

3 结论

本文构建了一种描述压电微位移平台输入电压和输出位移之间迟滞非线性关系的仿真模型，并给出了模型的原理和计算过程。 该模型是由迟滞算子模型和RBF 神经网络模型共同构成的。 模型输出结果和实验结果对比可以看出，其输出位移的最大误差仅为90 Hz 时的0.932 1 μm，最大均方误差为0.565 2 μm，最大相对误差为2.48%，表明模型的频率泛化能力较好，能够准确有效的描述压电陶瓷在10 Hz～90 Hz 的输入电压频率变化过程中的迟滞现象。 对于不同的压电作动器，只需要在模型中输入对应的压电数据，即可得到一种与之相对应的能准确有效的描述压电位移迟滞现象的模型，无需重新构建新的模型，而且在工程上易于实现，具有广泛的适用性，对非线性模型的建模具有一定的价值，也为下一步构建整体的控制系统奠定了基础。