基于改进小波阈值函数的闪电电场信号去噪研究∗

火元莲张 健连培君陈萌萌郑海亮

(西北师范大学物理与电子工程学院，甘肃 兰州730070)

闪电电场信号在采集、传输的过程中常常会受到噪声干扰[1]。 这会使所采集的信号发生一定程度的畸变，甚至有用的信号被噪声所淹没，进而影响后续信号处理的结果。 因此，如何有效去除闪电电场信号所包含的噪声，使闪电资料质量控制有进一步提升，已成为急需解决的问题。

目前，在闪电电场信号采集过程中的去噪主要依赖于硬件滤波电路，但这种技术对硬件电路要求较高[2]，去噪效果并不理想且成本较高。 因此对闪电电场信号去噪算法的研究引起了更多研究者的关注。 李鹏等人采用传统数字滤波和小波阈值法进行了闪电电场信号去噪的比较研究[3]。 赫伯特·罗哈斯等人采用自适应滤波器对雷电电场信号进行去噪[4]。 高太长、韩小东等人提出了一种基于多小波变换的闪电电场信号的去噪研究[5]。 火元莲等人提出了一种基于双密度双树小波变换的闪电电场信的去噪研究[2]。 赵媛芳等人提出了一种经验模态分解(EMD)和同步压缩小波变换(SST)相结合的去噪方法应用于闪电电场信号的去噪处理[1]。 在这些主要以小波分析为基础的去噪算法中，其中由Donoho 提出的阈值去噪算法因计算简单，去噪效果较好而在实际工程中得到了广泛应用[6-8]。 但这种阈值算法有着严重的缺陷，如硬阈值在阈值处不连续而软阈值存在恒定偏差问题[9]。 鉴于此，本文对阈值去噪算法进行了改进，提出了一种新的小波阈值算法，并将其应用于闪电电场信号的去噪处理中。改进的思路是综合软硬阈值函数和Garrote 阈值函数的基础上，通过引入一个在0 到1 之间可变的调整参数a 来克服原有的偏差性和不连续性，同时将小于阈值的小波系数不直接去除来达到保留闪电电场信号低频能量的目的。 与其他几种阈值方法的仿真结果表明，本文方法能够更好的消除信号中的噪声并保留有用的信息，具有更好的处理效果。

1 小波阈值函数的改进

1.1 小波阈值函数

选择一个合适的阈值函数在小波阈值去噪过程中至关重要。 常用的阈值函数有硬阈值函数、软阈值函数、半软阈值函数[10，12-13]以及Garrote 阈值函数。

硬阈值函数:

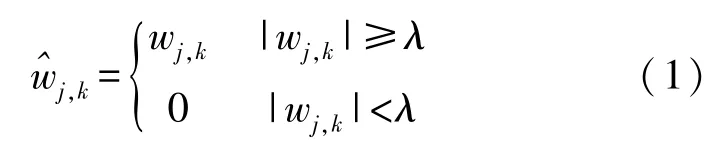
软阈值函数:

半软阈值函数:

Garrote 阈值函数:

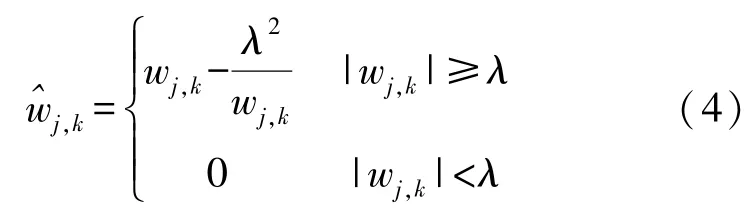
在上面四个式子中，λ表示阈值，wj，k表示信号在第j层k处的小波系数[7]，硬阈值函数在±λ处不连续，这种间断容易让信号产生伪吉布斯现象从而使重构信号产生震荡。 而软阈值函数虽然满足了连续的条件，但与wj，k之间存在恒定偏差，使得去噪后信号方差过大，这将直接影响重构信号与真实信号的逼近程度[13]。 半软阈值本身并没有克服软硬阈值的缺点，故仍然存在偏差性和不连续问题。 而Garrote 阈值函数具有很好的连续性，当｜wj，k｜≥λ时，其高阶可导，便于进行信号去噪；当｜wj，k｜→∞时，Garrote 阈值函数以为渐近线，克服了软阈值存在恒定偏差的缺点。 但Garrote 阈值函数忽略了噪声在小波变化下会随着尺度的增加而减小的特性。

1.2 改进的小波阈值函数

本文提出一种改进的小波阈值函数，其表达式如下:

可靠性监测与检测蕴含着一个巨大的可利用网络服务体系，能认识到它的作用才能走进真正的汽车维修行业网络服务时代。汽修“互联网+”未能成功的原因，就是很多人并不了解维修企业与客户之间的关系。汽车维修企业需要真正解决的问题是有效地解决客户问题，让客户走进企业并留住客户。注意，这里说的客户走进企业是指同一个客户先期认可性；而留住客户指的是该客户成为忠诚性客户。

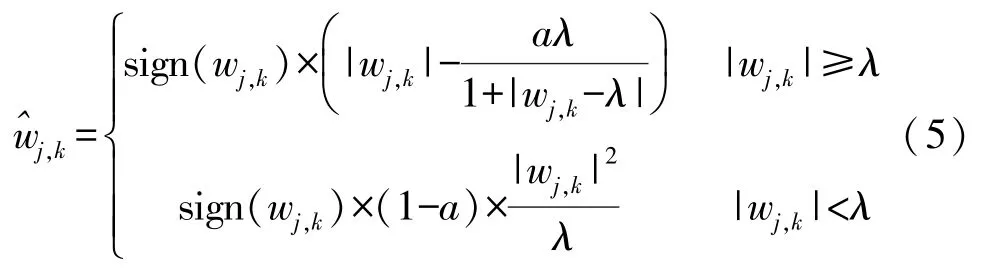
在式(5)中，a为调整参数，当a→0 时，式(5)近似于硬阈值函数。 当a→1 时，式(5)近似于软阈值函数，因此在实际应用中a可在0 到1 之间具体设定。 改进的阈值函数满足两个特征:①在(-∞，＋∞)内连续，克服了硬阈值函数不连续的缺点。②渐近线逐渐逼近硬阈值函数，克服了软阈值函数存在的偏差问题，并保留了低频能量信号。 其推导过程如下:

①逼近性

当wj，k>0 时，

同理可得，当wj，k<0 时，

综上，

的渐近线是

②连续性

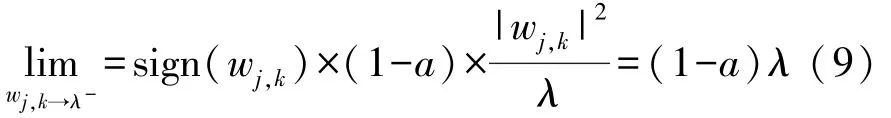
当ωj，k→λ＋时，

由式(9)、式(10)可知在λ处连续，同理可证，在-λ处，也连续，克服了硬阈值函数在±λ处不连续的缺点。

③偏差性

当wj，k>0 时，

当wj，k<0 时，

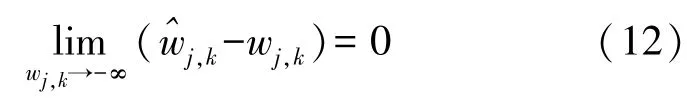
综上，随着wj，k→∞，逐渐逼近wj，k，克服了软阈值存在偏差的缺点。

2 改进小波阈值函数对闪电信号的去噪实验

2.1 改进小波阈值函数对标准闪电波形的去噪分析

标准闪电波形可归结为双指数衰减型脉冲波形，根据Wik M W 等人[14]的研究，标准的闪电波形可表示为

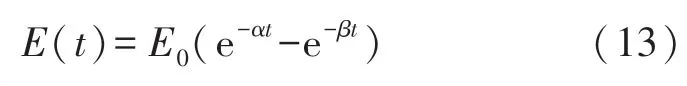
式中:E0为脉冲波形的幅值系数；α、β分别为波前、波尾衰减系数，本文仿真过程中E0＝30 V/m，α＝1.0×107，β＝1.5×106，采样频率fs＝6.0 MHz，在脉冲上叠加一个信噪比(SNR)为30 dB 的高斯白噪声。 分别利用硬阈值、软阈值、半软阈值、Garrote 阈值、改进小波阈值函数对含噪信号进行去噪处理。 小波基函数取sym6，分解层数选6 层。 仿真结果如图1 所示。 同时计算了均方根误差(RMSE) 和信噪比(SNR)[7]这两个指标用于分析原始信号和去噪信号的相似性。 信噪比越大，均方根误差越小，说明去噪效果越好。 这两个参数的定义如式(14)和式(15)所示，计算结果见表1。

图1 五种方法去噪效果图

表1 五种方法去噪结果比较

式中:f(k)为含噪信号，y(k)为小波降噪后的信号，N为信号的长度。

对不同噪声强度下几种算法的去噪效果做了比较，结果如图2 所示。 图中横坐标代表了不同的噪声强度，纵坐标代表了衡量算法去噪效果的均方根误差RMSE。

图2 不同噪声强度下各算法的均方根误差

从上述仿真结果可以看出本文的改进小波阈值法在标准闪电波形去噪中的优势。 而且随着噪声信号能量的增强(SNR 减小)，几种方法的去噪效果也随之降低，但总体来看本文算法的性能是最优的。

2.2 改进小波阈值函数对实测闪电电场信号的去噪分析

本文所用的实验数据来源于青海大通地区多站雷电观测实验中的闪电快电场变化测量仪，其时间常数为1 ms，输出动态范围±10 V，带宽100 Hz～5 MHz，采样频率为2.5 MHz。 在对闪电信号去噪之前，先对其进行归一化和去均值处理。 去均值就是对闪电电场信号进行零均值处理，由于采集过程中，闪电电场信号的距离大小不同即闪电强度也就不同，为了使实验数据变紧凑，对闪电电场信号进行归一化处理，即得到幅值范围统一的信号。 然后将本文算法与硬阈值函数、软阈值函数、半软阈值函数以及Garrote 阈值函数等算法应用于实测闪电电场信号的去噪，结果如图3 所示。 本文中小波基函数选择sym6，分解层数选择7 层。 从图3 中可以看出，软阈值与Garrote 阈值去噪后，闪电电场信号变得最为平滑，部分突变点消失，实际由于闪电这种非平稳信号的突变和尖峰处存在大量的有用信息，这种平滑直接会影响后期的时频分析及特征提取。 硬阈值和半软阈值的去噪效果略好于软阈值和Garrote 阈值去噪，但也平滑了信号中个别突变点部分，从而丢失一些重要信息。 只有本文算法在有效去噪的同时，很好的保留了闪电电场信号的细节信息和基本特征，便于进一步的分析和处理。

图3 五种方法去噪效果图

为进一步说明本文算法的有效性，随机选取5例地闪电场信号(GC)和5 例云闪电场信号(IC)，用本文方法和其余4 种算法进行去噪效果对比，去噪后的SNR 和RSME 分别如图4 和图5 所示。 从图可知，对不同噪声水平的共十个云、地闪电场信号进行去噪，本文提出的改进小波阈值函数方法对不同的闪电电场信号均具有最大的信噪比和最小的均方根误差，证明本文的去噪方法效果更好。

图4 5 种去噪方法下的信噪比

图5 5 种去噪方法下的均方根误差

3 结束语

本文提出了一种改进的小波阈值函数并将其应用于不同噪声强度的标准闪电波形和实测闪电电场信号的去噪实验中，结果表明，相比于硬阈值、软阈值、半软阈值和Garrote 阈值算法，本文算法的去噪效果是最优的。 这是因为提出的改进阈值函数可以通过调整参数a 使其具备了软硬阈值的优点，并克服了硬阈值函数在阈值处不连续以及软阈值函数存在恒定偏差的缺陷，在有效去除噪声的同时又较好的保留了原始闪电电场信号的细节信息，从而提高了闪电信号在后续处理过程中数据的可靠性。