复杂网络主动式入侵病毒扩散预测模型

郑 辉

(安徽工业经济职业技术学院 计算机与艺术学院，安徽 合肥 230051)

计算机的发展让网络的入侵也开始向大规模和多层次方向发展，这对人们的财产安全十分不利.这时，该如何预测网络在入侵下病毒的传播方向就成为了需要解决的问题[1].通过对大规模的网络入侵下病毒的传播方向进行预测并以模型的方式呈现受到大家的普遍关注，而且方法也很多[2-3].

殷守军[4]提出了一种用于确定病毒在大规模入侵过程中的传播方向的模型，通过与模糊推理方法相结合，利用模糊方法对收集到的网络病毒的传播方向进行划分，选择高概率网络入侵病毒的传播方向，通过概率推理方法，首先对网络病毒在网络入侵过程中的传播方式是如何退出的进行模糊分类，然后对网络入侵病毒在网络中的传播方向进行筛选，从而得出网络入侵病毒从一个方向向另一个方向传播的状态转移概率值，通过建立网络入侵过程中病毒在网络中的传播方向预测模型，提高网络入侵检测的准确性；针对传统舰船网络安全防护下入侵病毒检测性能差的问题，莫裕清[5]提出了一种检测和防范入侵病毒的研究方法，通过对收集到的网络传播信息进行编码，对其进行稀疏自编码，用神经网络算法对入侵病毒进行检测，再聚类提取其特征，建立入侵病毒的防御模型，从而保护舰船网络不受入侵病毒的干扰，实验表明，通过对入侵病毒的检测和防御，可以较传统方法提高31个百分点的防御效果，从而达到更好的防御效果.基于以上背景，本文设计了复杂网络主动式入侵病毒扩散预测模型，从而提高复杂网络主动式入侵病毒扩散的预测精度.

1 复杂网络主动式入侵病毒扩散预测模型设计

在对复杂网络主动式入侵病毒进行扩散预测过程中，先确定复杂网络主动式入侵意图，建立入侵意图攻击行为集函数.在此基础上，估计复杂网络主动式入侵病毒的扩散方程，基于扩散方程构建了复杂网络主动式入侵病毒扩散预测模型.

假设在复杂网络主动式入侵下提取到的病毒扩散特征为fi，得到复杂网络主动式入侵下病毒扩散的状态为

(1)

其中，Mi表示每一个病毒扩散特征的权值系数，confi表示复杂网络入侵下病毒扩散状态的观察序列，需要满足i=1,2,3,4…的条件.

复杂网络入侵病毒扩散转移概率计算公式为

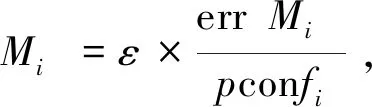
(2)

其中，ε表示复杂网络入侵病毒扩散被观测的概率.

根据以上过程得出的结论，构建复杂网络主动式入侵病毒扩散预测模型.

1.1 定义复杂网络主动式入侵行为

为了提高复杂网络主动式入侵病毒扩散预测精度，定义了复杂网络主动式入侵攻击行为[6]，制定了网络入侵攻击计划，获取到复杂网络主动式入侵意图.先定义复杂网络主动式入侵行为，即

(3)

其中，Xi和Xj分别表示i时刻和j时刻的网络入侵攻击行为，W{Xi,Xj}表示i时刻和j时刻的网络入侵攻击行为之间存在的因果关系，d″wergv表示复杂网络主动式入侵行为的类型集合，j′jkl表示有效的网络入侵攻击计划权重.

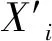
(4)

其中，p′werkk表示复杂网络中每一个攻击节点的独立性分布情况，d′dfg表示复杂网络入侵行为的随机变量集r′wert的联合概率分布.

令复杂网络主动式攻击之间的因果关系权重为η′sd[7]，那么获取到复杂网络主动式入侵意图为

(5)

其中，s′sde表示复杂网络主动式入侵行为在相邻时刻内的条件概率，v′fhj表示复杂网络主动式入侵病毒扩散的联合概率分布，h′hjk表示复杂网络主动式入侵行为在节点变量上的转移概率，k′kl表示复杂网络主动式入侵行为的类型权重.

在复杂网络主动式入侵病毒扩散预测过程中，引入Deep Belief Nets理论定义了复杂网络主动式攻击行为，通过制定复杂网络主动式入侵攻击计划，得到复杂网络主动式入侵意图，确定了复杂网络主动式入侵意图攻击行为集函数.

1.2 主动式入侵病毒扩散过程估计

在复杂网络主动式入侵的影响下，计算机病毒扩散过程都是以非线性的形式存在的，而不具有扩散叠加特征[8].采用传统的评估模型[9]，估计复杂网络主动式入侵病毒扩散过程，无法界定复杂网络主动式入侵强度，也会导致复杂网络主动式入侵病毒扩散过程的估计误差较大[10]，具体过程如下

Step1：计算复杂网络主动式入侵因子，描述复杂网络主动式入侵的具体情况，计算公式为

(6)

其中，x1和y1表示复杂网络主动式入侵行为的初始特征向量，x2和y2表示复杂网络主动式入侵行为改变后的特征向量，n表示复杂网络主动式入侵次数，h表示复杂网络主动式入侵的特征系数.

Step2：计算复杂网络主动式入侵病毒扩散过程估计系数，描述复杂网络主动式入侵病毒扩散过程的预测状态，计算公式为

(7)

其中，i表示复杂网络主动式入侵的次数序号.

Step3：计算复杂网络主动式入侵病毒扩散过程估计系数的预测准确率，公式为

(8)

以上三个步骤可以预测复杂网络主动式入侵病毒扩散过程系数，实现复杂网络主动式入侵病毒扩散过程的估计，在复杂网络主动式入侵的影响下，病毒扩散过程具有不可控制的扩散性和随机性[11]，传统的病毒扩散过程评估模型无法在复杂网络建模中界定复杂网络主动式入侵强度，由于无法预判复杂网络的主动式入侵强度，假设入侵强度一直处于一定的阈值和时间内，导致复杂网络主动式入侵病毒扩散过程的估计结果存在误差.

1.3 构建病毒扩散预测模型

在构建复杂网络主动式入侵病毒扩散预测模型过程中，以复杂网络主动式入侵病毒扩散过程的评估结果为依据，利用概率推理的方式[12]，计算复杂网络主动式入侵病毒在扩散过程中的状态转移概率值，基于此，构建复杂网络主动式入侵病毒扩散预测模型.

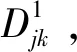
(9)

其中，pj表示复杂网络主动式入侵病毒扩散过程中的初始状态概率分布值，pR表示复杂网络主动式入侵下的病毒扩散随机变量.

令复杂网络主动式入侵下病毒扩散的转移函数为W，计算公式为

(10)

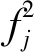
在复杂网络主动式入侵病毒扩散预测模型构建过程中，假设D1和D2表示复杂网络主动式入侵下病毒扩散预测样本的补偿系数，xmax表示复杂网络主动式入侵下病毒扩散依存的最大经验权值，xmin表示复杂网络主动式入侵下病毒扩散依存的最小经验权值，如果在有限的时间内，复杂网络主动式入侵下病毒扩散的条件概率变化过程对方向集合是平稳的[14]，那么得到复杂网络主动式入侵病毒扩散的联合分布概率为

(11)

其中，itermax表示复杂网络主动式入侵下病毒扩散的观察函数，利用公式(11)计算复杂网络主动式入侵病毒扩散的目标函数，公式为

(12)

其中，Z(t)表示复杂网络主动式入侵病毒在t时刻的扩散方向[15]，pa表示复杂网络主动式入侵病毒的扩散状态集合，p表示复杂网络主动式入侵病毒的扩散方向集合，Z(t-1)表示复杂网络主动式入侵病毒扩散状态Y(t-1)的新方向.

将复杂网络主动式入侵病毒扩散预测模型的训练集表示为

(13)

其中，X(t)表示复杂网络主动式入侵病毒扩散状态集函数.

如果Z(t-1)决定着Z(t)，那么构建复杂网络主动式入侵病毒扩散状态的转移公式为

(14)

根据以上过程推导，构建了复杂网络主动式入侵病毒扩散预测模型，表示为

(15)

具体算法流程如图1所示.

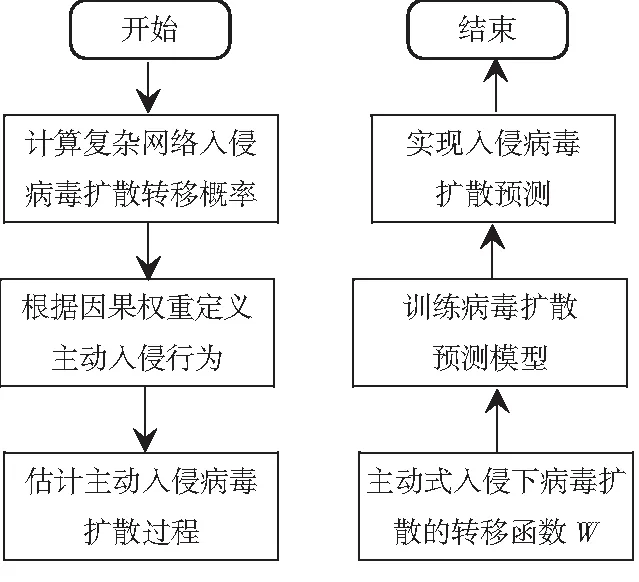
图1 复杂网络主动式入侵病毒扩散预测流程

综上所述，通过确定复杂网络主动式入侵意图攻击行为集函数，估计了复杂网络主动式入侵病毒扩散过程，以复杂网络主动式入侵病毒扩散过程的评估结果为依据，构建了复杂网络主动式入侵病毒扩散预测模型，实现了复杂网络主动式入侵病毒扩散的预测.

2 实验对比分析

为了验证提出的复杂网络主动式入侵病毒扩散预测模型是有效的，模拟Internet环境下的子网，尽量在不同局域网内进行实验，并选择35台电脑对外开放通信地址.为了减轻病毒对计算机的危害，选择VBS脚本病毒进行实验.实验硬件环境：AMD Ryzen 7 5800X 3.8GHz 处理器，8 GB内存空间.实验软件环境：Windows 10操作系统，MATLAB R2019a.实验数据集采用复杂网络中的NSL-KDD数据集，为实验测试提供了一个网络连接数据.在数据集中随机抽取部分数据作为训练样本与测试样本，其中训练集正常记录数为3672，攻击记录数为2045；测试集正常记录数为3673，攻击记录数为2261.基于上述实验环境，分别引入文献[4]的预测模型和文献[5]的预测模型，从精确度、时间效率和预测误差三个方面进行实验测试.

三个病毒扩散预测模型的精确度和时间效率测试结果如表1所示.

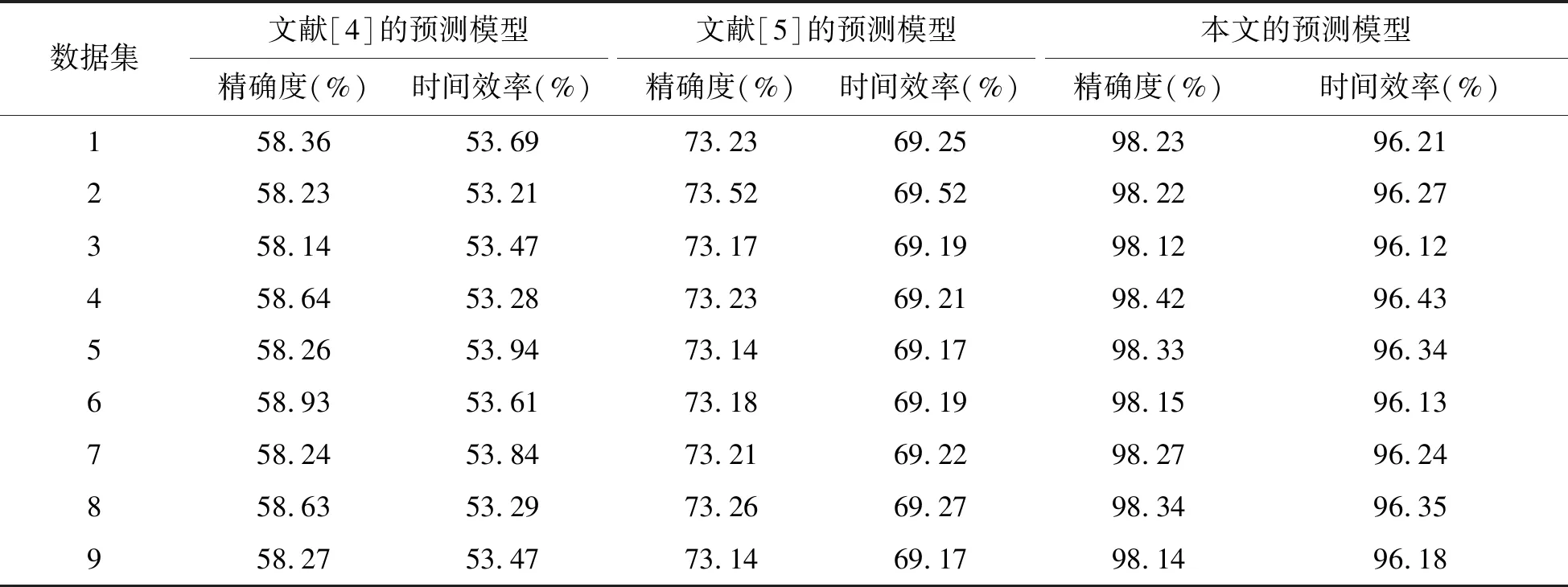
表1 结果统计

从表1的结果可以看出，采用本文设计的复杂网络主动式入侵病毒扩散预测模型在精确度和时间效率两个方面的有效性，明显高于其他两个病毒扩散预测模型，原因是本文设计的复杂网络主动式入侵病毒扩散预测模型在预测之前，确定了复杂网络主动式入侵意图攻击行为集函数，通过复杂网络主动式入侵病毒扩散状态转移的计算，从而提高了模型的有效性.

三个病毒扩散预测模型的预测误差测试结果如图2所示.

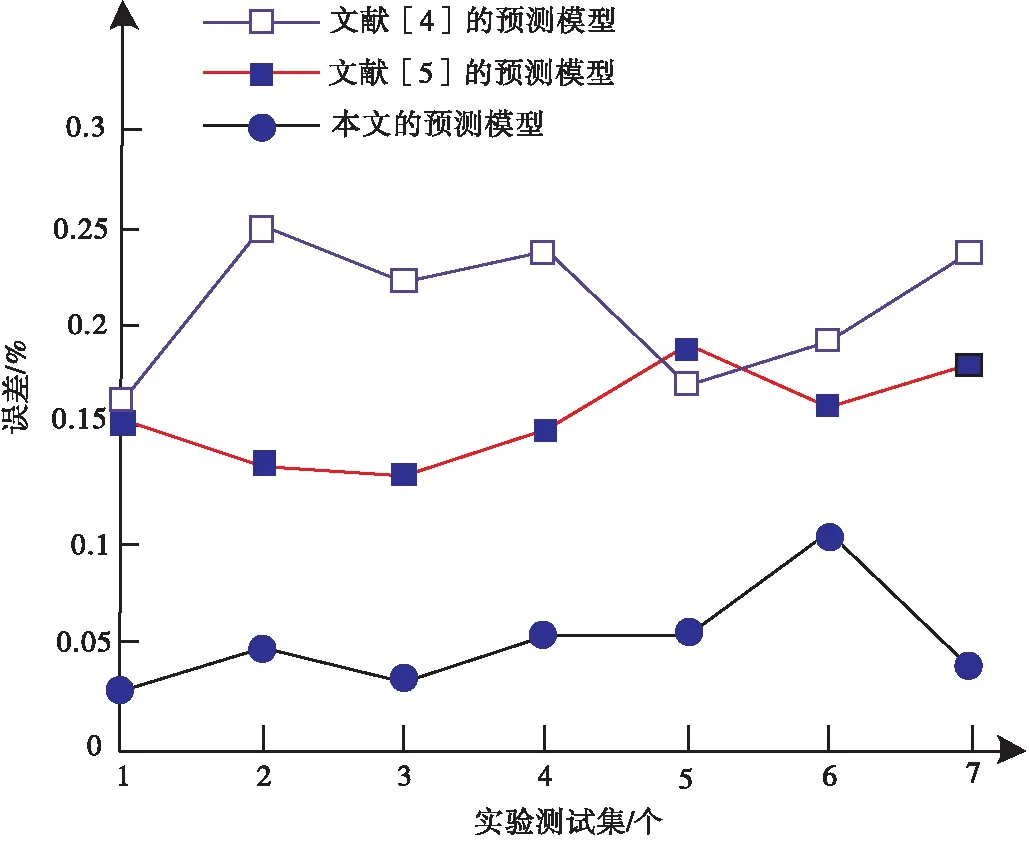
图2 预测误差测试结果

从图2的结果可以看出，采用本文设计的复杂网络主动式入侵病毒扩散预测模型在误差率上，远远低于其他两个病毒扩散预测模型，原因是本文设计的病毒扩散预测模型，针对入侵病毒在扩散过程中具有不确定性，推理出扩散过程中的状态转移概率值，保证了该模型在复杂网络主动式入侵病毒扩散预测中的精确度.

3 结束语

本文提出了复杂网络主动式入侵病毒扩散预测模型，通过确定复杂网络主动式入侵意图攻击行为集函数，估计了复杂网络主动式入侵病毒扩散过程，以复杂网络主动式入侵病毒扩散过程的评估结果为依据，构建了复杂网络主动式入侵病毒扩散预测模型，实现了复杂网络主动式入侵病毒扩散的预测.结果显示，该预测模型具有更高的精度.