三元广义欧拉函数方程φ(xyz)=φ2(x)+φ2(y)+φ2(z)的解
2021-05-15梁晓艳
梁晓艳,高 丽,高 倩
(延安大学 数学与计算机科学学院,陕西 延安 716000)
欧拉函数φ(n)与广义欧拉函数φ2(n)在数论中都有着重要的作用,近年来,有关欧拉函数的性质以及欧拉方程吸引了很多学者的兴趣.在文献[1-3]中研究了二元欧拉函数方程φ(ab)=k(φ(a))+φ(b))的正整数解.文献[4]研究了三元欧拉函数方程中φ(xyz)=φ(x)+φ(y)+φ(z)+6的正整数解.文献[5]研究了四元欧拉方程φ(abcd)=φ(a)+2φ(b)+3φ(c)+4φ(d)的正整数解.文献[6]研究了包含欧拉函数的方程φ(φ(n))=2w(n)的所有正整数解,文献[7-8]分别研究了广义欧拉函数φ2(φ(n))=φ(φ2(n))与φ2(m)=2w(m)3w(m)的正整数解。文献[9]研究了二元广义欧拉函数方程φ(ab)=11φ2(a)+13φ2(b)的正整数解.本文通过参阅上述文献,利用整数的分解以及初等数论的相关知识研究了三元广义欧拉函数方程φ(xyz)=φ2(x)+φ2(y)+φ2(z)的正整数解.
1 相关引理


引理3[10]当n≥2时,有φ(n) 定理 三元广义欧拉函数方程φ(xyz)=φ2(x)+φ2(y)+φ2(z)共有12组正整数解,其解为(x,y,z)=(1,2,3),(2,1,3),(3,1,2),(3,2,1),(1,3,2),(2,3,1),(1,1,2),(1,2,1),(1,2,2)(2,1,1),(2,1,2),(2,2,1). 证明对于三元广义欧拉函数方程 φ(xyz)=φ2(x)+φ2(y)+φ2(z), (1) 根据x,y,z的不同取值范围将分为四种情况进行讨论. 情况1:当x,y,z中只有一个属于[1,2]时,假设x=1,2. 即 2φ(yz)=φ(y)+φ(z). (2) 设(y,z)=d,存在正整数y1,z1,使得φ(y)=y1φ(d),φ(z)=z1φ(d),由式(2)可得 从而有 2dy1z1=y1+z1, 分解可得(2dy1-1)(2dz1-1)=1,根据整数的分解可得以下关系式 当d=1时,得y1=1,z1=1,则 φ(y)=1,φ(z)=1,y=z=1,2, 与假设矛盾,所以方程无解. 因为x,y,z的位置是等同的,所以当y=1或z=1时同理可证方程无解. (ii)当x=2时, φ(xyz)=φ(2yz)=1+φ2(y)+φ2(z). 由引理2和引理3得 2φ(2yz)=2+φ(y)+φ(z)≥φ(y)φ(z), φ(y)φ(z)-φ(y)-φ(z)≤2, (φ(y)-1)(φ(z)-1)≤3. ①当(φ(y)-1)(φ(z)-1)<0时,则φ(y)<1或φ(z)<1,由引理3知,方程无解. ②当(φ(y)-1)(φ(z)-1)=0时,则φ(y)=1或φ(z)=1,则y=1,2或z=1,2,因为y,z属于[3,+∞),所以方程无解. ③当(φ(y)-1)(φ(z)-1)=1时,则有 由引理3知,方程无解. ④当(φ(y)-1)(φ(z)-1)=2时,则有 φ(y)=2,φ(z)=3或φ(y)=3,φ(z)=2. 由引理3知,方程无解. ⑤当(φ(y)-1)(φ(z)-1)=3时,则有 φ(y)=4,φ(z)=2或φ(y)=2,φ(z)=4, 当φ(y)=4,φ(z)=2时, xyz=5,8,10,12,y=5,8,10,12,z=3,4,6,经检验,方程无解. 当φ(y)=2,φ(z)=4时, xyz=5,8,10,12,z=5,8,10,12,y=3,4,6,经检验,方程无解. 因为x,y,z的位置是等同的,所以当y=1,2或z=1,2时,同理可证方程无解. 情况2:当x,y,z中只有两个属于[1,2]时. 假设x,y∈[1,2],则有(x,y)=(1,1)(1,2)(2,1)(2,2)四种情况. (i)当(x,y)=(1,1)时, φ(xyz)=φ(z)=φ2(z), (ii) 当(x,y)=(1,2)时,φ(xyz)=φ(2z)=1+φ2(z),由引理4得 解得φ(z)≤2,即φ(z)=1,2,又因为φ(xyz)为偶数,所以φ(z)=2,z=3,4,6,φ(xyz)=2,xyz=3,4,6,又因为xy=2,所以z=3,所以方程有解(x,y,z)=(1,2,3). (iii)当(x,y)=(2,1)时, φ(xyz)=φ(2z)=1+φ2(z), 由引理4得 解得φ(z)≤2,即φ(z)=1,2. 因为φ(xyz)为偶数,所以φ(z)=2,z=3,4,6,φ(xyz)=2,xyz=3,4,6,又因为xy=2,所以z=3,所以方程有解(x,y,z)=(2,1,3). (vi)当(x,y)=(2,2)时, φ(xyz)=φ(4z)=1+1+φ2(z)=2+φ2(z), 由引理4得 解得φ(z)≤4,即φ(z)=1,2,3,4. 因为φ(xyz)为偶数,所以φ(z)=4,z=5,8,10,12,φ(xyz)=4,xyz=5,8,10,12,又因为xy=4,经检验,方程无解. 当x,z∈[1,2]或y,z∈[1,2]时,同理可证方程有解(x,y,z)=(3,1,2),(3,2,1),(1,3,2),(2,3,1). 情况3:当x,y,z都属于[1,2]时.有(x,y,z)=(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2)八种情况. (i)当(x,y,z)=(1,1,1)时, φ(xyz)=φ(1)=1≠0, 所以(x,y,z)=(1,1,1)不是方程的解. (ii)当(x,y,z)=(1,1,2)时, φ(xyz)=φ(2)=1=φ2(2)=1, 所以(x,y,z)=(1,1,2)是方程的解. (iii)当(x,y,z)=(1,2,1)时, φ(xyz)=φ(2)=1=φ2(2)=1, 所以(x,y,z)=(1,2,1)是方程的解. (vi)当(x,y,z)=(1,2,2)时, φ(xyz)=φ(4)=2=φ2(2)+φ2(2)=2, 所以(x,y,z)=(1,2,2)是方程的解. (v)当(x,y,z)=(2,1,1)时, φ(xyz)=φ(2)=1=φ2(2)=1, 所以(x,y,z)=(2,1,1)是方程的解. (vi)当(x,y,z)=(2,1,2)时, φ(xyz)=φ(4)=2=φ2(2)+φ2(2)=2, 所以(x,y,z)=(2,1,2)是方程的解. (vii)当(x,y,z)=(2,2,1)时, φ(xyz)=φ(4)=2=φ2(2)+φ2(2)=2, 所以(x,y,z)=(2,2,1)是方程的解. (viii)当(x,y,z)=(2,2,2)时, φ(xyz)=φ(8)=4≠φ2(2)+φ2(2)+φ2(2)=3, 所以(x,y,z)=(2,2,2)不是方程的解. 情况4:当x,y,z都属于[3,+∞)时,由引理2,引理3,引理4得 即 2φ(xyz)=φ(x)+φ(y)+φ(z)≥φ(x)φ(y)φ(z), φ(x)+φ(y)≥(φ(x)φ(y)-1)φ(z), φ(x)+φ(y)≥φ(x)φ(y)-1, 整理得 (φ(x)-1)(φ(y)-1)≤2. 根据φ(x),φ(y)的取值下面分四种情况进行讨论. (i) 当(φ(x)-1)(φ(y)-1)<0时,则 φ(x)<1或φ(y)<1, 由引理3知,方程无解. (ii) 当(φ(x)-1)(φ(y)-1)=0时,则 φ(x)=1或φ(y)=1, 则x=1,2或y=1,2,因为x,y,z都属于[3,+∞);所以方程无解. (iii)当(φ(x)-1)(φ(y)-1)=1时,则有 φ(x)=φ(y)=2,x=y=3,4,6, 经检验,方程无解. (iv)当(φ(x)-1)(φ(y)-1)=2时,则有 φ(x)=2,φ(y)=3或φ(x)=3,φ(y)=2. 当φ(x)=2,φ(y)=3时,则有 2φ(xyz)=5+φ(z), 由引理3知,方程无解. 当φ(x)=3,φ(y)=2时,则有 2φ(xyz)=5+φ(z), 由引理3知,方程无解. 综上所述,证毕.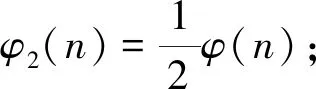
2 结论及证明