基于人工神经网络的偏微分方程求解方法*
2021-05-15刘文慧石琳郭勇袁冬芳
刘文慧,石琳,郭勇,袁冬芳*
(1.内蒙古科技大学 信息工程学院,内蒙古 包头 014010;2.内蒙古科技大学 理学院,内蒙古 包头 014010)
微分方程常用的数值方法有Runge-Kutta方法、线性多步方法、预测校正方法、有限元、有限差分和有限体积等[1,2].传统的数值方法计算存储量和计算时间严重制约了高维问题的求解.近年来,人工神经网络在图像识别技术,语音识别和文本分析得到巨大的应用[3-5].在电力系统[6]方面、化学工程[7]和环境工程等[8]领域引入神经网络方法来解决各自领域未能解决的任务.经过证明,多层神经网络可以逼近任何非线性函数,因此利用这个良好的性质对微分方程的求解进行研究.
1997年LAGARIS等[9]开始用人工神经网络对常微分方程研究,通过算例看出求解的高精度和泛化性.JIANYUA用径向基神经网络来求解椭圆型偏微分方程[10].后来,相关研究人员利用小波神经网络研究非线性函数一阶导数的逼近[11].LEE S T[12]基于小波神经网络,利用蝴蝶优化算法求解二维椭圆偏微分方程,最后从算例说明其算法的高精度和高效率性.
1 神经网络结构
神经网络由最初的单层感知器发展到现在的多层神经网络结构.多层结构的神经网络具有更大容量,可逼近更大更复杂模型.神经网络的基本结构是由神经元构成,如图1,神经元有输入信号和输出信号.两者信号之间通过神经元内部决定,神经元的数学模型有Sigmoid函数,Tanh函数,Relu函数等.不同的场景应用的激活函数不同.
图1 单个神经元结构图
采用Sigmoid函数作为激活函数.其公式为
(1)
相关理论证明多层神经网络可逼近任何非线性函数.采用3层神经网络作为训练模型,模型见图2.3层神经网络的基本结构由输入层、隐藏层和输出层组成,其中输入和输出的关系见式(2).
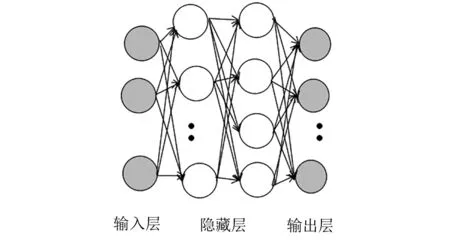
图2 3层神经网络示意图
N(X)=w2φ(w1φ(wX+b)+b1) .
(2)
当神经网络结构确定后,要对神经网络进行学习,优化出逼近真实模型的神经网络参数.学习之前需要设置1种衡量的指标来判断真实模型和逼近模型的误差.常用的误差公式是均方差函数,对于m个训练样本{(x1,y1),(x2,y2)…(xm,ym)},神经网络输出{n1,n2…,nm},则根据均方差函数建立损失函数为:
(3)
神经网络模型是关于权值w和阈值b的函数,不同的权值和阈值表示不同的模型.神经网络主要对权值和阈值进行学习,在每次迭代后更新w和b逼近真实模型.当损失函数建立后,选择1种神经网络学习方法.神经网络学习的方法有梯度下降法和共轭梯度法.梯度下降法常作为神经网络的学习规则.权值和阈值学习规则为:
wt=wt-1+Δw,
(4)
bt=bt-1+Δb,
(5)
(6)
(7)
式中:η为学习率,学习率太大不容易收敛,太小导致神经网络学习速度过慢.
2 神经网络求解微分方程方法
微分方程的一般形式及定解条件可描述为:
(8)
对于某个具体的方程既要满足微分,还要满足边界条件约束为
(9)
为了采用神经网络求解微分方程,将损失函数构造为两项和的形式,如式(10).损失函数中的第一项满足对微分方程的约束,如式(11),第二项满足对边界条件的约束,如式(12).
Loss=LossMSE,D+LossMSE,B.Cs,
(10)
(11)
LossMSE,B.Cs=mean((N(xB.Cs)-Ψ(XB.Cs))2+(N(XB.Cs)-Ψ(XB.Cs))2+(2N(XB.Cs)-2Ψ(XB.Cs))2+…(nN(XB.Cs)-nΨ(XB.Cs))2) .
(12)
3 数值算例
考察4个微分方程算例来进行说明.
算例1:
其中求解的区间在[0,1].该方程的边界条件
该方程的解析解
Ψ(x)=-2ln(1+x2) .
选择具有2个隐藏层,10个神经元,学习率为0.001的3层神经网络进行模型训练.
由图3可见,神经网络得到的近似解和解析解十分相似,平均误差在千分之一.为进一步说明神经网络的高精度特性,将真实模型的一阶导数和二阶导数与神经网络的一阶导数和二阶导数进行对比,对比图如图4所示,由图可看出神经网络近似解的一阶即二阶导数和真实解导数的误差也在千分之一.神经网络的精度比传统精度有着很大提升.为了验证模型的精度,在方程定义区间随机选取100个点样本进行测试验证,可看出测试样本的精度和解析解也是十分吻合,如图5所示.
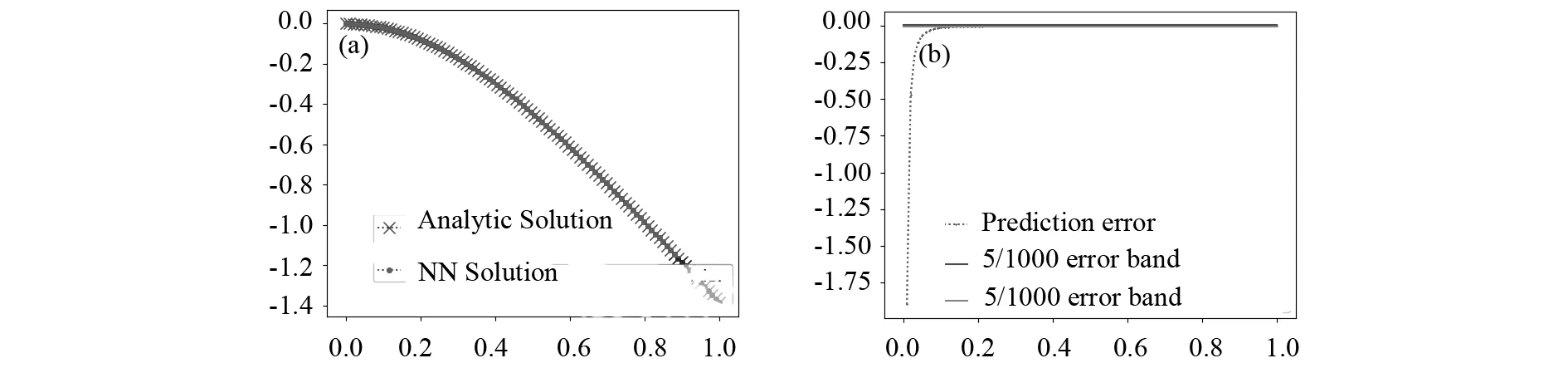
图3 算例1训练模型和真实模型及其误差图(a)神经网络训练和真实模型图;(b)训练和真实模型误差图

图4 算例1训练模型和真实模型一阶导及二阶导图(a)神经网络训练和真实模型一阶导;(b)神经网络训练和真实模型二阶导
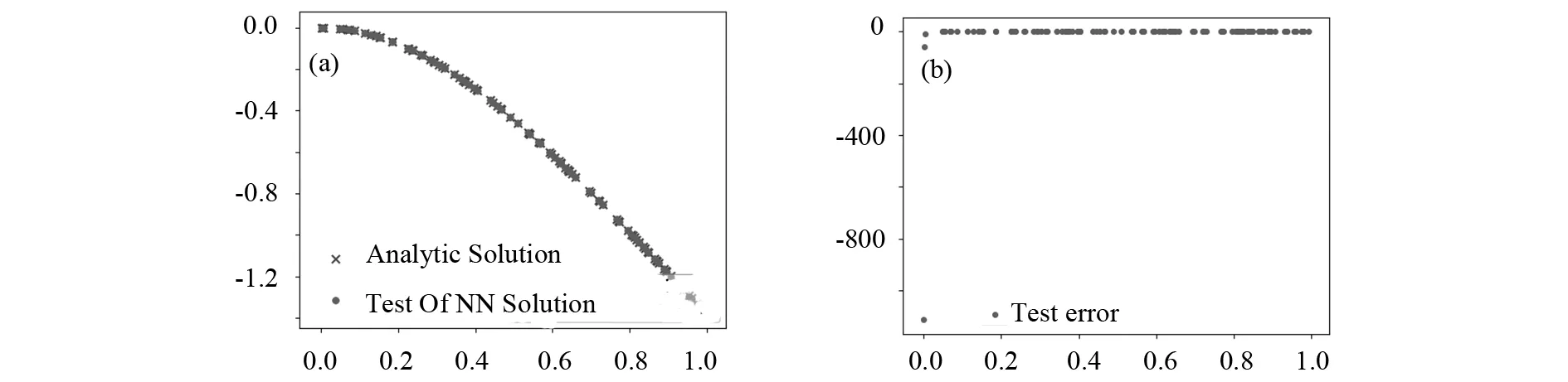
图5 算例1测试模型和真实模型及其误差图(a)神经网络测试和真实模型图;(b)测试和真实模型误差图
算例2:
边界条件:
φ(0,y)=0,φ(1,y)=0,
φ(x,0)=0,φ(x,1)=sin(πx) ,
定义区间[0,1]×[0,1],方程解析解
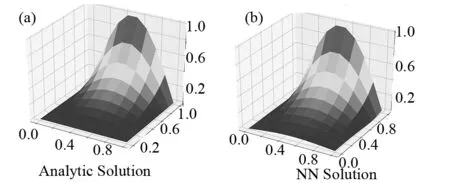
图6 算例2解析解和神经网络训练解图(a)真实模型图;(b)神经网络训练模型

图7 算例2解析解和神经网络训练解绝对误差图
算例3:考察二阶偏微分方程.
边界条件:
φ(0,y)=y3,φ(1,y)=(1+y3)e-1,
φ(x,0)=xe-x,φ(x,1)=(1+x)e-x,
求解范围[0,1]×[0,1],方程解析解
φ(x,y)=e-x(x+y3) .

图8 算例3解析解和神经网络训练解图(a)真实模型图;(b)神经网络训练模型

图9 算例3解析解和神经网络训练解绝对误差图
算例4考察二阶偏微分方程:
其中:
边界条件:
φ(0,y)=ey+2-1(1+y)2
φ(1,y)=ey-1+2-1(1+y)2
φ(x,0)=e-x+2-1,φ(x,1)=e1-x+2
求解范围[0,1]×[0,1],方程解析解为:
φ(x,y)=ey-x+2-1(1+y)2

图10 算例4解析解和神经网络训练解(a)真实模型图;(b)神经网络训练模型

图11 算例4解析解和神经网络训练解绝对误差图
4 结论
采用神经网络方法对偏微分方程的求解提供了1种通用的解决方案.基于神经网络的方法与传统数值方法相比优势在于良好的泛化性以及高效的求解效率.通过4个算例充分说明神经网络方法能够精确的逼近微分方程的真实解.方法为微分方程的求解提供了新的解决方案.此外,将继续针对边界梯度较大的微分方程研究基于神经网络的求解方法.
