一个新四维超混沌系统及其在图像加密中的应用*

2021-05-15黄迎久

内蒙古科技大学学报 2021年1期

黄迎久

(内蒙古科技大学工程训练中心，内蒙古包头 014010)

随着互联网技术的快速发展，图像、视频等多媒体信息已成为网络传输的主要信息载体，同时其安全问题也成为网络安全方面的热点课题.由于混沌系统具有初值敏感、伪随机数离散度高等优点，目前已被广泛应用于信息安全领域，尤其在图像加密[1-5]方面.但是低维的混沌系统由于具有较低的Lyapunov指数和狭小的混沌区间等缺陷，使得在图像加密算法中容易导致密钥空间偏小和离散度偏低等漏洞，因此，运用低维混沌系统的图像加密算法极有可能被成功破解[6-9].近几年的研究表明，基于混沌系统的图像加密算法，其安全性很大程度依赖于混沌系统动力学行为的复杂性，而四维以上的超混沌系统其动力学行为更为复杂，是目前图像加密算法的主要应用系统[10-13].

文中新构建了1个四维的超混沌系统，具有较高的Lyapunov指数，更为宽广的混沌区间，能够克服密钥空间偏小等缺陷.文中的图像加密算法结合了与明文相关联的方法，将图像分块分解，并采用了两轮次不同的置乱和扩散过程.

1 新构建的四维超混沌系统

(1)

式中：当a=14，b=36，c=7,m=4，p=-1，k=-10时，式(1)处于超混沌状态，部分相图如图1所示.

2 基本动力学行为分析

2.1 耗散性

对于式(1)，有

(2)

根据耗散性理论可知，式(1)将以e△t指数速度收敛，当t→∞时，系统的体积元V会以e△t的速率趋近于零，所以式(1)为耗散性系统，因此确定式(1)存在混沌吸引子.

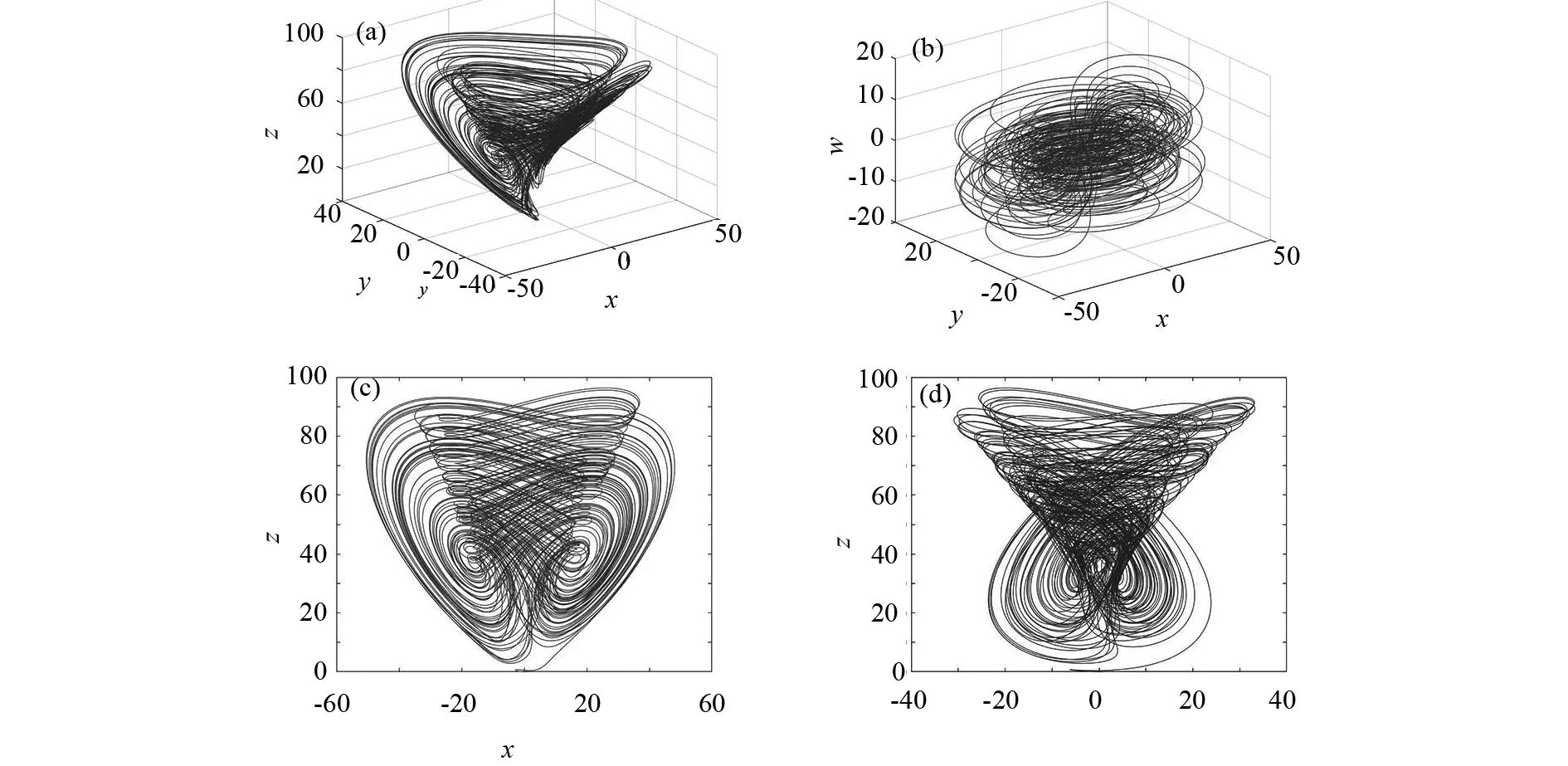
图1 系统相图(a)x-y-z方向；(b)x-y-w方向；(c)x-z方向；(d)y-z方向

2.2 平衡点

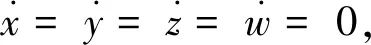
(3)

得(0,0,0,0)为式(3)的唯一解，因此，P(0,0,0,0)为式(1)仅有的1个平衡点，则在平衡点P的雅可比(Jacobian)矩阵为：

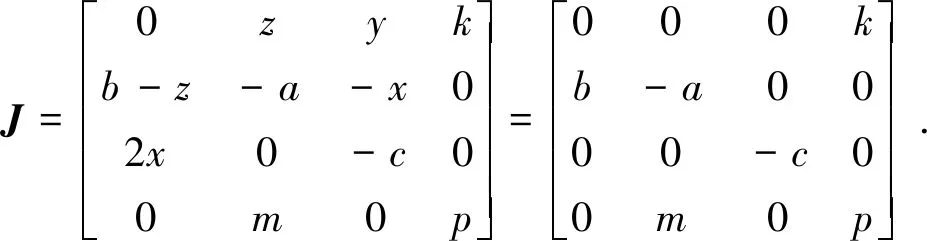
(4)

设λ为特征根，I为四阶单位矩阵，求解行列式|λI-J|=0，得到4个特征根：λ1=-18.465 2，λ2=1.732 6+8.659 3i，λ3=1.732 6-8.659 3i，λ4=-9.其中，λ2和λ3均具有正的实数部分，根据Routh-hurwitz判断条件，确定平衡点P(0,0,0,0)为不稳定的鞍点.因此，系统存在混沌吸引子.

2.3 Lyapunov指数

Lyapunov指数是衡量非线性动力系统混沌状态的1个重要的指标系数.当具有1个正的Lyapunov指数时，为混沌状态；当具有2个或以上正的Lyapunov指数时，为超混沌状态.

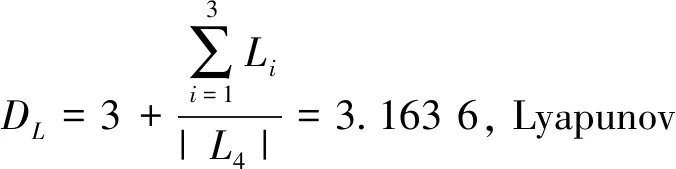
图2 Lyapunov指数谱图

2.4 庞加莱截面分析

庞加莱截面上的截点分布形状，可以验证非线性动力系统的混沌状态.若截面上出现大量截点，并且呈现片状且具有分形的结构时，则系统处于混沌状态.

图3为x-z和y-z方向上的庞加莱截面图.图中的大量截点呈现分支形状，因此确定式(1)处于混沌状态.

图3 庞加莱截面图(a)x-z方向；(b)y-z方向

3 图像加密算法

图像加密流程如图4所示.测试图像选用分辨率为256×256的灰度图Airport，Lena和Peppers，图像加密效果如图5所示.

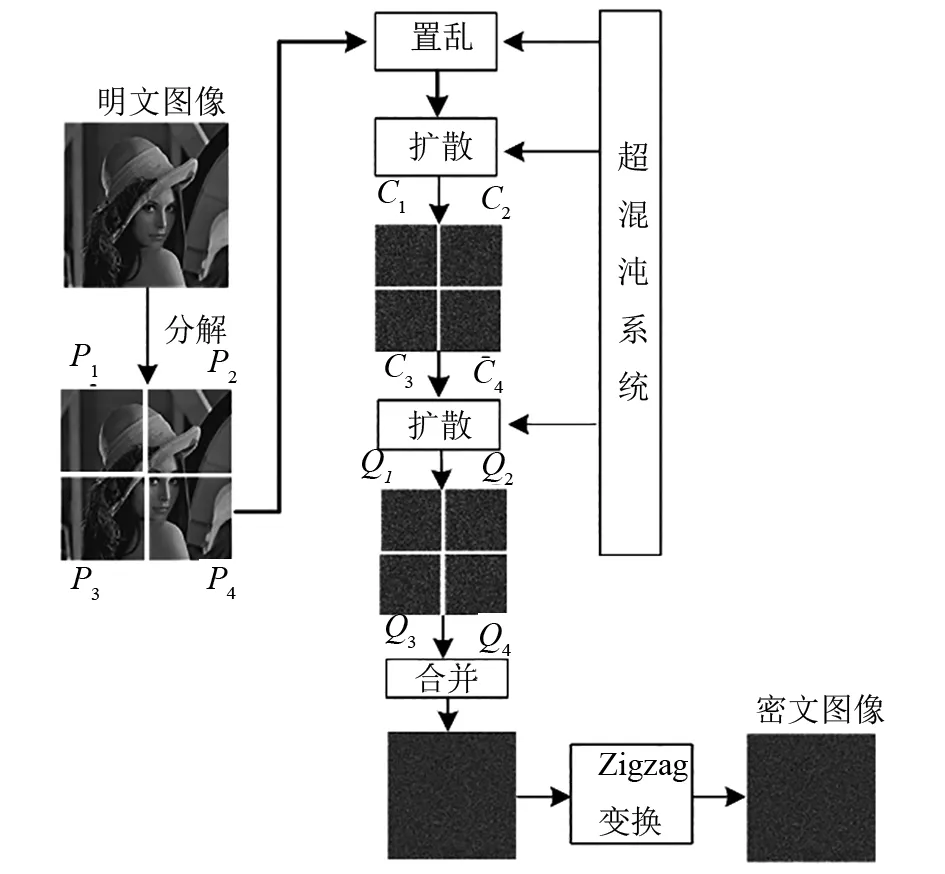
图4 图像加密流程图

图像加密算法具体过程如下：

(1)将明文图像P平均分解为4个分块P1，P2，P3，P4.

(2)第一次置乱.将P1，P2，P3，P4对应的像素点按以下方法进行对换位置.

取P1中的像素点P1(i1,j1)：

若(i1+j1)mod4=1，则P1(i1,j1)与P2(i1,j1)进行对换；若(i1+j1)mod4=2，则P1(i1,j1)与P3(i1,j1)进行对换；若(i1+j1)mod4=3，则P1(i1,j1)与P4(i1,j1)进行对换.

取P2中的像素点P2(i2,j2)：

若(i2+j2)mod4=2，则P2(i2,j2)与P4(i2,j2)进行对换；若(i2+j2)mod4=3，则P2(i2,j2)与P3(i2,j2)进行对换.

取P3中的像素点P3(i3,j3)：

若(i3+j3)mod4=0，则P3(i3,j3)与P4(i3,j3)进行对换.

(3)任取超混沌系统的一组初始值，如(x0=0.1,y0=0.1,z0=0.1,w0=0.1)，带入式(1)，采用四阶龙格-库塔迭代法，迭代N次(N>500)，取出一组迭代的值{x(N-100),y(N-100),z(N-100),w(N-100)}，根据以下公式分别将其转换为整数：

i(x(N-100)×264+w(N-100)×264)mod128 ，

(5)

j(y(N-100)×264+z(N-100)×264)mod128 .

(6)

(4)从P1，P2，P3，P4中各自1个像素点Pm(i,j)，m=1,2,3,4.根据以下公式生成4个值k1，k2，k3，k4.

(7)

得到一组密钥key={x0+k1,y0+k2,z0+k3,w0+k4}.

获取明文图像P的高度H与宽度W，利用密钥key结合根据四阶龙格-库塔迭代法，迭代式(1)20 000次，获取4个长度均为H×W的伪随机序列S1，S2，S3，S4.

利用以下公式将4个伪随机序列转换为4个H×W的二维矩阵M1，M2，M3，M4.

Mi=(|Si|×264)mod256，i=1,2,3,4 .

(8)

(5)按照明文图像分解的方法，将M1和M2分别分解为与P1，P2，P3，P4同样大小的4个矩阵M11，M12，M13，M14；M21，M22，M23，M24.

共享云。包含外文期刊数据库元数据、外文期刊（含纸本）元数据、外文期刊论文元数据、外文期刊核心目录元数据、外文期刊论文引文元数据等若干元数据，主题规范词表、学科规范词表、机构规范词表以及管理统计分析指标体系、管理统计分析系统。

(6)第一次扩散.根据下列公式将P1，P2，P3，P4中每一个像素点的值进行变换.

C1=(P1⊕M11)mod256⊕M21

C2=(P2⊕M12)mod256⊕M22

C3=(P3⊕M13)mod256⊕M23

C4=(P4⊕M14)mod256⊕M24.

(9)

(7)第二次扩散.将M3和M4分别分解为与C1，C2，C3，C4同样大小的4个矩阵M31，M32，M33，M34；M41，M42，M43，M44.根据下列公式将C1，C2，C3，C4中每1个像素点的值进行变换.

Q1=((C1⊕M31)+M41)mod256

Q2=((C2⊕M32)+M42)mod256

Q3=((C3⊕M33)+M43)mod256

Q4=((C1⊕M34)+M44)mod256 .

(10)

(8)第二次置乱.按Q1，Q3，Q2，Q4的顺序合并成为1个H×W的矩阵T，顺时针旋转90°；而后采用根据文献[14]改进的Z字形变换，对矩阵T进行置乱，如图6所示.

图5 Airport加密与解密效果图(a)明文图像；(b)加密图像；(c)还原图像

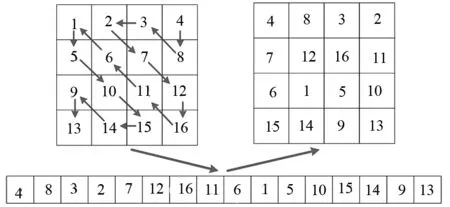
图6 Z字形变换图

最终得到的T矩阵就是加密图像的像素矩阵.

加密图像的解密过程为图像加密的逆过程，这里就不重复叙述.

4 仿真测试

4.1 密钥空间分析

若式(1)的密钥K={k1,k2,k3,k4}.其中k1，k2，k3，k4是由明文分块P1，P2，P3，P4中各取1个像素点计算而生，若明文图像分辨率为256×256，各分块大小均为128×128，按64位CPU的计算能力来估算，密钥K的每一个分量的浮点数运算精度均可达到1064，其则密钥K的取值空间至少可达到232×10256，可见密钥空间足够大，完全可以抵御针对密钥的暴力破解.

4.2 直方图分析

由于明文图像的相邻像素点之间具有一定的关联关系，所以其直方图一般表现为波浪形状，而加密图像的相邻像素点间的相邻关系已被彻底打乱，因而其像素点均匀而密集分布在1个矩形区域内.

图7为测试图像Lena的明文图像直方图与加密图像直方图.

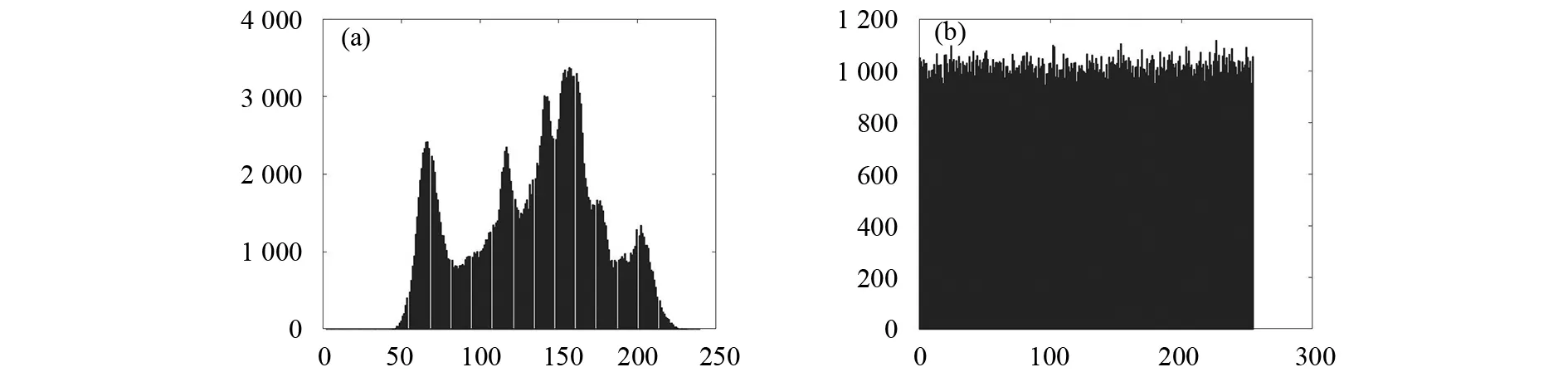
图7 Lena直方图(a)明文图像直方图；(b)加密图像直方图

4.3 相关系数分析

相关系数是衡量相邻像素之间关联性的1个指标系数.相关系数越趋近于1，相邻像素点之间的相关性越高；相关系数的值越趋近于0，相邻像素点之间的相关性越低.加密图像的相关系数越低，就表明加密算法的安全性越高.相关系数的计算公式如下：

(11)

(12)

(13)

(14)

式(12)～(14)中：xi和yi为2个相邻像素点的灰度值，N(N≥4000)为选取像素点的样本数.

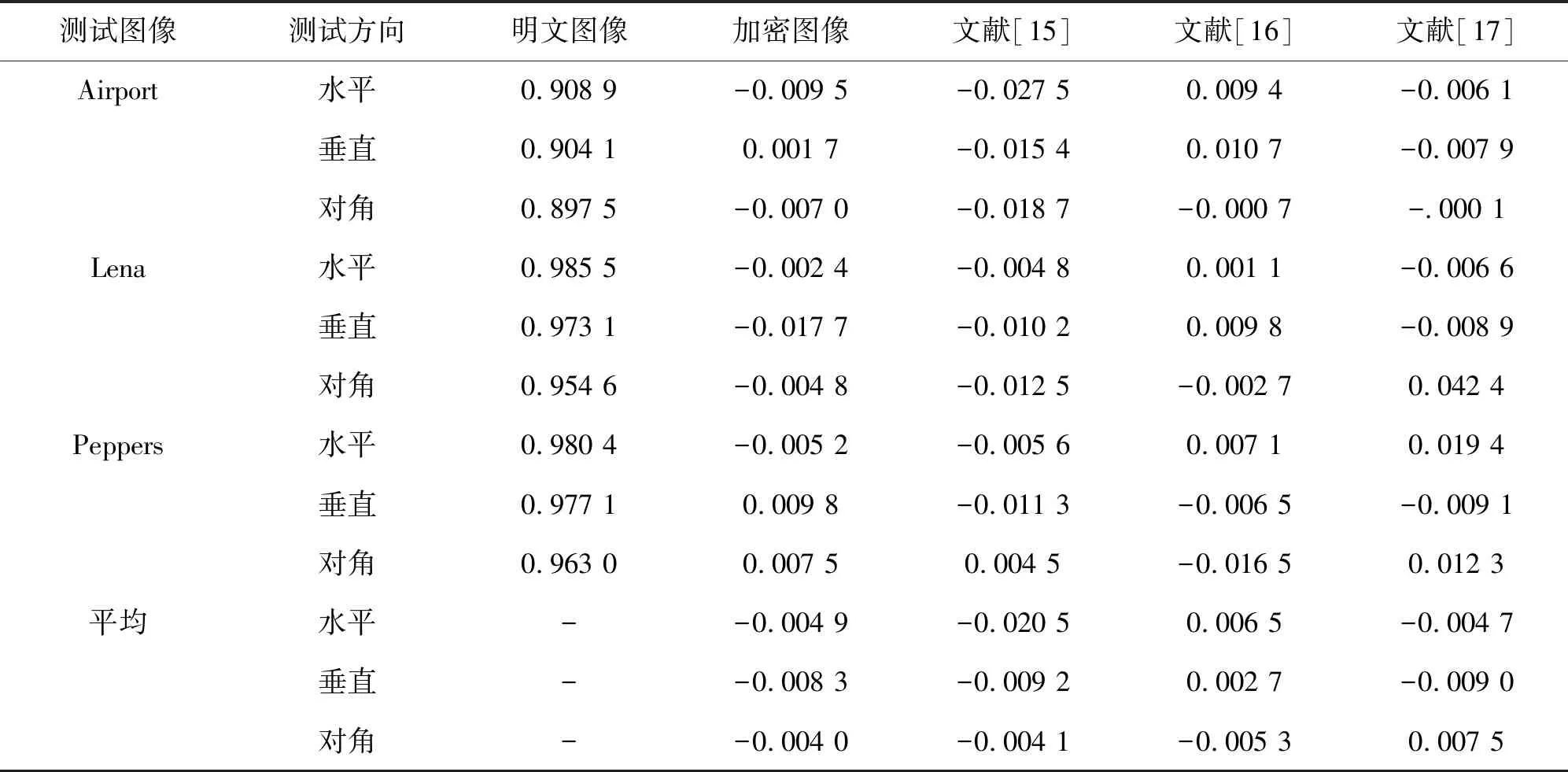
表1 相关系数测试结果表

从表1的测试结果可以确定：加密图像的相关系数都趋近于0，表明加密算法已彻底破坏了相邻像素点之间的关联关系，使得加密图像中很难直接获取明文图像的原始像素，可见文中加密算法的性能优于文献[15]，[16]，[17]的加密算法.

图8，9为测试图像Peppers的明文图像和加密图像的相邻像素相图，其中横、纵坐标均代表像素点的灰度值.

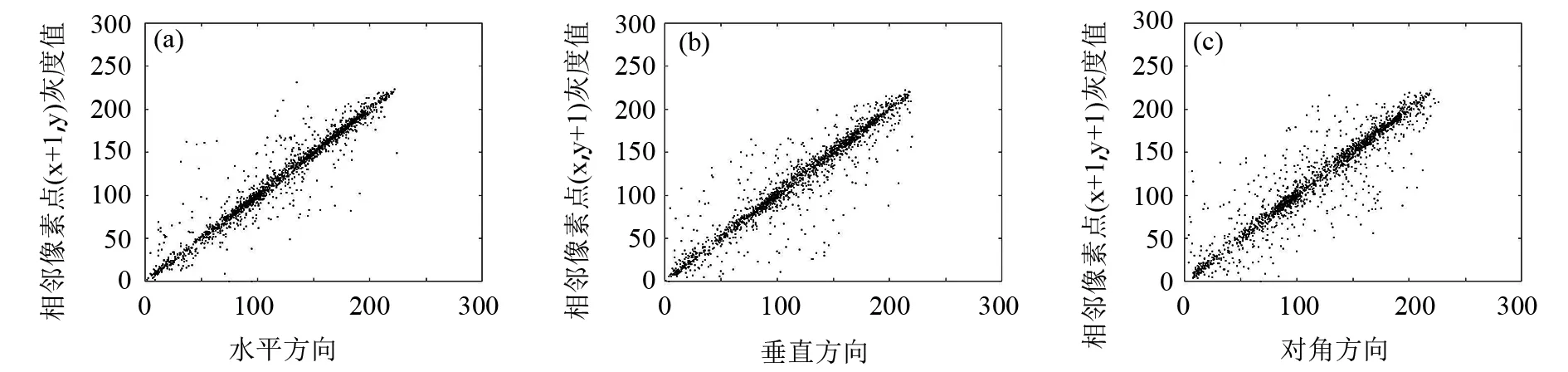
图8 Peppers明文图像相邻像素方向相图(a)水平方向；(b)垂直方向；(c)对角方向

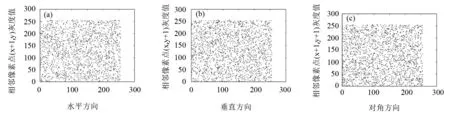
图9 Peppers加密图像相邻像素方向相图(a)水平方向；(b)垂直方向；(c)对角方向

图8中，像素点都密集地聚集在1条线段上，也证实了明文图像的相邻像素点之间具有密切的关联性；图9中，加密图像的像素点都散布在1个矩形区域内，也证实了加密图像的相邻像素点已完全不具备关联性.

4.4 明文图像敏感性分析

明文图像敏感性是指当明文图像的一些像素点的灰度值被改变后，用同一密钥加密后，不同加密图像之间的差异程度.加密图像之间的差异越大，加密的效果越好，抵御差分攻击能力越强.通常用像素改变率(number of pixels change rate,NPCR)和归一化平均改变幅度(unified average changing intensity,UACI)2个指标系数来进行评测.NPCR和UACI的计算公式如下：

(15)

(16)

(17)

式(15)～(17)中：H和W为图像的高和宽，C1(i,j)、C2(i,j)为2个不同加密图像的像素点的灰度值.其中，NPCR的理论最佳值为99.605 4%，UACI的理论最佳值为33.463 5%.

表2 NPCR和UACI测试结果表

表2的测试结果显示，NPCR和UACI的测试结果非常接近于理论最佳值，优于文献[15]，[16]，[17]的测试结果.

4.5 密钥敏感性分析

密钥的敏感性是指当密钥发生极其微小的改变后，2个加密图像之间产生的差异程度.密钥敏感性越强，加密图像所产生的差异程度越大，表明加密算法的安全性越高.

令密钥Key={0.1,0.01,0.001,0.000 1}，将其4个分量分别进行微小的扰动，产生4个不同的密钥，Key1={0.1+10-10,0.01,0.001,0.000 1}，Key2={0.1,0.01+10-10,0.001,0.000 1}，Key3={0.1,0.01,0.001+10-10,0.000 1}，Key4={0.1,0.01,0.001,0.000 1+10-10}.用密钥Key对明文图像Lena进行加密，再分别用密钥Key1，Key2，Key3，Key4对加密图像进行解密，解密效果如图10所示.

从图10看出，4个密钥均无法正确还原出明文图像，表明图像加密算法的密钥敏感性极强，完全有能力抵御针对密钥的暴力攻击.