基于振动台试验的刚构桥近断层效应动力响应分析

闫晓宇 赵 卓 王 卓

(1.国家开放大学理工教学部, 北京 100039; 2.天津大学滨海土木工程结构与安全教育部重点实验室, 天津 300072；3.北京工业大学城市建设学部， 北京 100124)

为了适应我国西北黄土深壑和西南山区等特殊地质、地形条件，大跨度刚构桥被广泛应用。不同墩高的刚构桥抗震性能差别较大，属于典型的非规则桥梁，且当跨度较大时，地震动空间效应不可忽略。Bonganoff等的研究[1]发现，应考虑地震动传播的时滞性对大跨度结构的影响。此后，地震动场效应得到越来越多国内外学者的重视，并成为桥梁结构抗震领域的热点问题之一。研究[2-5]表明：大跨度桥梁结构地震响应与输入地震动的特性及具体结构形式紧密相关；多点激励对其影响不可忽略，在抗震分析时应加以考虑；桥梁结构各部位对多点激励的敏感程度因结构形式不同而差异较大。

西南山区属于地震频发地区，如2008年的汶川地震给当地造成了极大的破坏，百花大桥就是在该次地震中损毁的，有研究结果表明除了桥梁自身因素外，近断层效应是导致其失效的诱因之一[6]。因此，有必要对近断层地震作用下刚构桥的抗震性能做深入研究。BERTER等最先注意到近断层地震动中所含的脉冲对建筑结构的影响[7]，此后关于近断层地震动的研究引起了学者们的普遍关注。现有研究成果[8-12]表明：近断层地震动对结构地震响应的影响在各国抗震设计标准中均未有明确规定。与远场地震相比，近断层地震动作用下的建筑结构，基底剪力、层间位移更大，结构的变形需求更大。近断层地震动将影响桥梁结构损伤发生的位置和类型。总的来说，近断层地震动作用机理较为复杂，现有研究结果多数为定性研究，想要得到定量结果，并应用于抗震设计标准，还需要大量的理论分析和试验研究结果作为支撑。

鉴于此，本文以某座高墩大跨度刚构桥为研究背景，对1∶10比例的3跨刚构桥模型进行多点激励的缩尺模型振动台台阵试验，在此基础上建立模型桥有限元模型，选取各10条典型的近断层和远场地震动进行地震响应加载及有限元结果对比分析，以期得出对该类桥梁抗震设计有参考价值的结论。

1 缩尺模型振动台试验

试验原型为一座3跨高墩大跨钢筋混凝土刚构桥，桥跨布置为35 m+60 m+35 m。主桥上部结构为单箱单室变截面钢筋混凝土箱梁，下部结构为空心薄壁矩形墩。综合考虑实验室试验场地条件、1 m×1 m振动台台阵承载能力等，将试验模型几何缩尺比例确定为1∶10，如图1所示。表1为模型物理量相似关系。

a—模型桥平面布置; b—缩尺模型照片。图1 试验-刚构桥 mmFig.1 Diagrams of the rigid-framed bridge

表1 模型物理量及其相似关系Table 1 Similarity relations of main physical quantities

试验中选取三条天然地震动记录，分别为El Centro波(1940年美国加州)、汶川波(2008年中国汶川)及北京波(1976年中国唐山)。按照8度设防，试验地震峰值加速度aPGA调整为1.1g。地震动空间差动效应主要表现为行波效应、局部场地效应、波的衰减效应和部分相干效应。试验中，行波效应采用地震激励相位差的方法实现，即利用各个桥墩墩底作动器启动的时间差来模拟实际地震激励下行波效应的影响。局部场地的变化通过在各个支承处输入不同自功率谱的地震波来考虑，试验中采用了文献[13]中的公式。试验量测物理量：主跨跨中、桥墩墩底、墩梁固接节点等位置的应变响应；墩顶、主梁、台面等位置的加速度响应；桥墩变形(即墩顶相对墩底的位移)。

2 试验结果分析

通过白噪声输入法得到模型动力特性，纵向一阶频率约为8.17 Hz，振型为纵桥向弯曲变形，与数值模拟结果相吻合。对于刚构桥，桥墩、墩梁固接节点为主要易损区域，故主要针对以上位置的动力响应进行对比分析。为了明确多点激励(包含行波效应、局部场地效应)的影响，定义无量纲参数D=Rt/R0，其中，Rt为考虑多点激励时的结构响应，R0为不考虑多点激励时的结构响应。

图2为各工况桥墩墩底、固接节点混凝土应变峰值，图3为各工况桥墩变形(墩顶、墩底相对位移)峰值。由图2和图3可知：行波效应与一致激励相比，增大了各个桥墩的变形和受力，并且由于约束形式不同、刚度不同，各桥墩受到行波效应的影响程度也不同。与边墩相比，中墩受到的影响更大；与桥墩相比，墩梁固接节点受到的影响略小。与一致激励相比，局部场地效应增大了各个桥墩的变形和受力，降低了墩梁固接节点处应变响应，说明其对该处的受力是有利的。固接节点应变响应的变化幅度小于桥墩墩底处，说明节点不如桥墩对场地土质的改变敏感。相较于单独考虑一致激励下，单独考虑行波效应或单独考虑局部场地效应的情况，考虑多点激励后，桥墩的地震反应均有增大。而墩梁固接节点处的应变响应不一定大于行波效应或场地效应单独作用下的应变响应。这说明，在地震动空间差动效应中仅考虑某一因素的影响，将使得大跨度刚构桥的地震影响分析结果不准确。

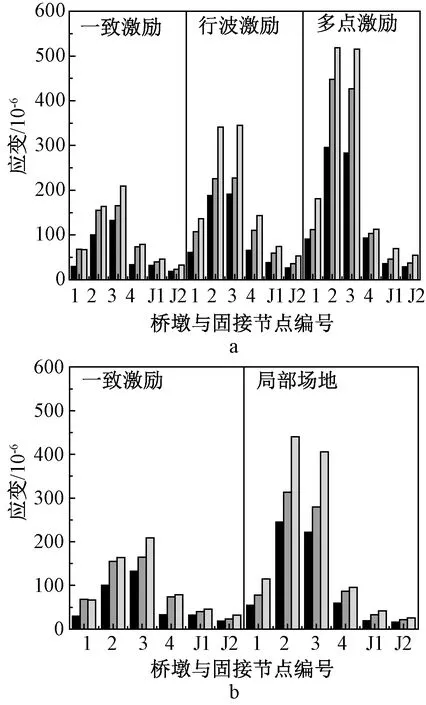
a—多点激励; b—局部场地效应。El Centro波; 汶川波; 北京波。图2 桥墩墩底、固接节点混凝土应变峰值Fig.2 Peak strain of concrete for pier bases and joints

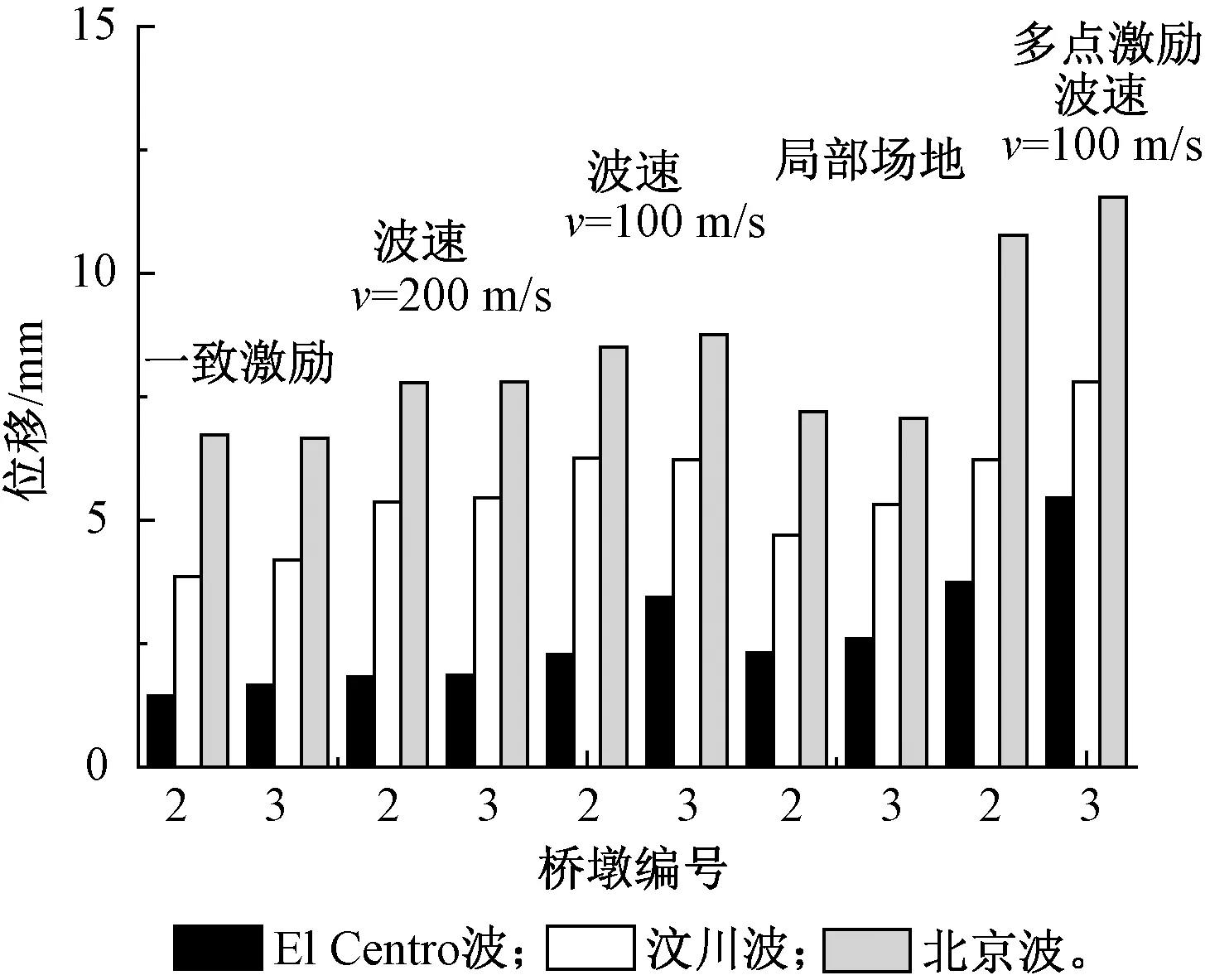
图3 墩顶墩底相对位移响应峰值Fig.3 Peak relative displacement of piers

3 近断层刚构桥地震响应分析

3.1 近断层效应

为了研究近断层地震对桥梁结构地震响应的影响，自美国太平洋地震工程研究中心(PEER)地震数据库选取常见的10条远场地震动及10条近断层地震动进行分析，见表2；调整后地震波的峰值地面速度与峰值地面加速度的比值aPGV/aPGA如图4a所示，可以看出：与远场地震动相比，近断层地震动具有较大的aPGV/aPGA；为进一步说明近断层地震的特点，以TCU063、Taft波为例，绘制其时程曲线及反应谱对比图(图4d)，可以看出：当反应谱周期大于0.2 s时，近断层地震动的反应谱谱值远大于远场地震动的谱值。

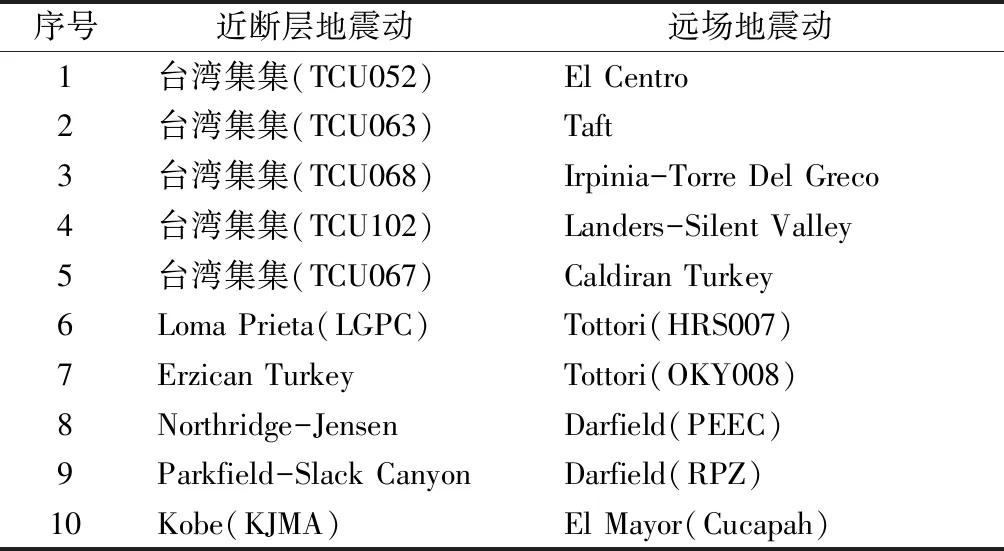
表2 选用的地震动Table 2 Selected ground motion

为了明确近断层地震对结构动力响应的影响，定义无量纲参数D=Rn/R0，其中，Rn为考虑近断层地震时的结构响应，R0为不考虑近断层地震时的结构响应。

图5a为近断层地震动作用下模型桥各个桥墩墩顶的水平相对位移峰值曲线；图5b为远场地震动作用下模型桥各个桥墩墩顶的水平相对位移峰值曲线。如图5a所示：10条近断层地震动中，TCU063作用下，桥墩墩顶水平位移峰值最大，4个桥墩墩顶位移峰值分别为4.54,13.94,13.97,3.08 mm，Erzican Turkey作用下，桥墩水平位移峰值最小，分别为2.47,6.72,6.73,1.66 mm。10条远场地震动中，Taft波作用下，桥墩水平位移峰值最大，4个桥墩墩顶位移峰值分别为1.92,5.76,5.76,1.45 mm；Tottori(HRS007)作用下，桥墩水平位移峰值最小，分别为0.62,1.71,1.71,0.48 mm。以Taft波为标尺，2号桥墩为例，近断层地震动作用下，水平位移峰值放大系数分别为6.61、7.26、4.17、4.79、4.67、4.95、3.50、7.17、5.76、4.96；以Taft波为标尺，1号桥墩为例，近断层地震动作用下，水平位移峰值放大系数分别为2.32、2.37、1.58、1.80、1.55、1.65、1.28、2.26、1.88、1.45，可以看出：中墩(2号墩)比边墩(1号墩)水平相对位移增幅更大，对近断层效应更敏感。与远场地震动相比，近断层地震增大了桥墩相对位移。由图5c看出：对于墩底弯矩响应有相似规律，且位移响应峰值、弯矩响应峰值变化规律与aPGV/aPGA无明显相关性。

a—aPGV/aPGA比值图; b—Taft时程曲线; c—TCU063时程曲线; d—反应谱对比。图4 选用地震动的特征Fig.4 Characteristics of selected ground motion

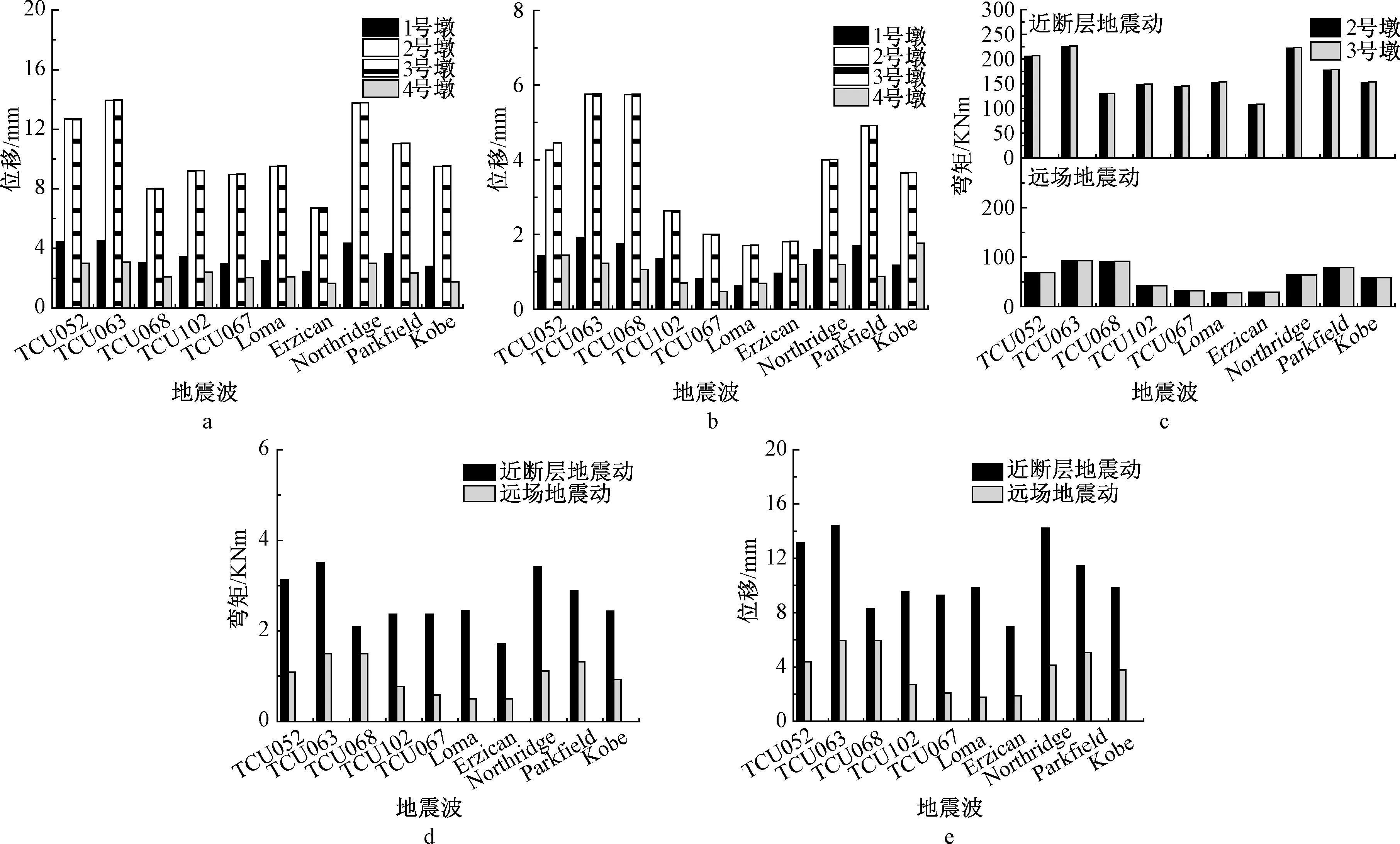
a—近断层地震动; b—远场地震动; c—墩底弯矩峰值; d—主梁跨中弯矩峰值曲线; e—主梁水平位移峰值曲线。图5 模型动力响应峰值Fig.5 Peak dynamic responses of the model

图5d为主梁跨中弯矩峰值曲线，10条近断层地震动中，TCU063作用下，主梁弯矩峰值最大，为3.510 kN·m，Erzican Turkey作用下，主梁弯矩峰值最小，为1.714 kN·m。10条远场地震动中，Taft波作用下，主梁弯矩峰值最大，为1.496 kN·m；Tottori(HRS007)作用下，主梁弯矩峰值最小，为0.499 kN·m。以Taft波为标尺，放大系数最大为2.35，最小为1.15。可以看出：与远场地震动相比，近断层地震对主梁跨中受力影响显著。主梁跨中弯矩响应峰值变化规律与aPGV/aPGA无明显相关性。与桥墩相比，主梁受力放大系数较小，桥墩对地震波的变化更敏感。

图5e为主梁水平位移峰值曲线，10条近断层地震动中，TCU063作用下，主梁水平位移峰值最大，为14.42 mm，Erzican Turkey作用下，水平位移峰值最小，为6.95 mm。10条远场地震动中，Taft波作用下，主梁水平位移响应峰值最大，为5.96 mm；Tottori(HRS007)作用下，水平位移响应峰值最小，为1.77 mm。可以看出：与远场地震动相比，近断层地震增大了主梁水平位移。

综上，大多数近断层地震较远场地震对刚构桥地震响应更为不利，结构抗震设计应加以考虑，从而使分析结果更精准。

3.2 地震动空间效应

选取使结构响应最大的TCU063波、使结构响应最小的Erzican Turkey波及Kobe波，进行考虑地震动空间效应的动力响应分析。图6为近断层地震动作用下，考虑行波效应的刚构桥墩顶水平相对位置峰值曲线。可见：TCU063作用下，桥墩位移峰值最大，4个桥墩墩顶位移峰值分别为4.54，13.94，13.97，3.08 mm；考虑行波激励后，放大系数为1.31、1.72、1.79、1.30；考虑多点激励后，放大系数为1.97、2.23、2.36、1.95；Erzican Turkey作用下，桥墩位移峰值最小，分别为2.47，6.72，6.73，1.66 mm；考虑行波后，放大系数为1.10、1.49、1.44、1.17；考虑多点激励后，放大系数为1.51、1.93、1.88、1.53。与一致激励相比，行波激励增大了桥墩相对位移，多点激励使得影响更剧烈；与边墩相比，中墩受行波激励的影响更大。

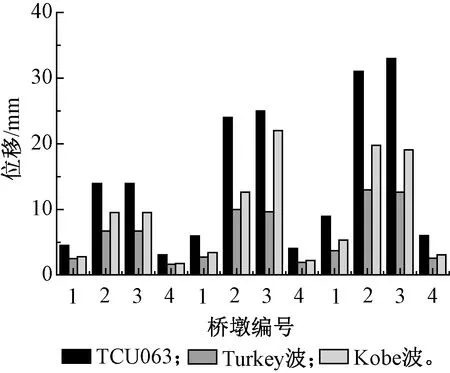
图6 近断层地震下桥墩水平相对位移响应峰值Fig.6 Peak relative displacement of the model subjected to near-fault earthquake excitation

因此考虑地震动空间效应后，刚构桥桥墩动力响应进一步增大；近断层效应与地震动空间效应共同考虑时，情况最为不利。

4 结束语

通过对一座1∶10比例的三跨刚构桥模型的多点激励振动台台阵试验，在此基础上建立了刚构桥有限元模型，选取10条典型近断层地震动和10条远场地震动，对其作用下的动力响应进行分析对比，得出以下结论：

1)行波激励对桥墩变形、受力均为不利因素，其影响程度与视波速取值密切相关；各部分所受影响程度排序为中墩、边墩、固接节点，即中墩比边墩对场地变化(视波速、场地土质等)更敏感，桥墩比固接节点对场地类型的改变更敏感；局部场地效应使墩梁固接节点处应变响应降低，说明局部场地效应对固接节点受力有利；多点激励下，桥墩动力响应大于一致激励、行波激励或局部场地效应的结果，但固接节点无此规律，这说明应综合考虑地震动空间差动效应中各个因素的影响，使刚构桥地震影响分析结果更为准确。

2)与远场地震动相比，近断层地震动aPGV/aPGA的比值更大，模型结构动力响应更剧烈；考虑近断层效应后，桥墩变形和受力均发生增长，以Taft波为标尺，边墩变形增大了1～2倍，中墩变形增大了2～7倍，主梁跨中弯矩、水平位移也相继增大，增幅1～2倍；中墩动力响应受到的影响比边墩大，桥墩比主梁受到的影响大；考虑多点激励后，这种不利影响被加剧了。因此，近断层效应、地震动空间效应在抗震设计均应该予以考虑，使分析结果更准确，并且在抗震设计时，要根据地震波、结构特性等因素共同考虑，具体问题具体分析。