结合自适应更新策略和再检测技术的跟踪算法

马 珺，王昱皓

太原理工大学 物理与光电工程学院，太原030600

计算机视觉已经在许多领域得到运用，其中目标跟踪作为其重要的组成部分，已经成为研究的热点问题。目标跟踪在商业领域中可以用于智能监控、人机交互、行人与车辆的视频监控；军事领域中可以用于无人机侦察监视、敌对目标的自动定位和追踪；虽然经过多年的发展，目标跟踪技术已经取得了长足的进步。但由于跟踪对象运动的不可预知性和所处环境的复杂性，目标跟踪仍然存在许多亟待解决的难点。由于目标跟踪存在遮挡（Occlusion）、形变（Deformation）、快速运动（Fast Motion）、背景杂波（Background Clutters）、光照变化（Illumination Variation）、超出视野（Out-of-View）、平面内旋转（In-Plane Rotation）、平面外旋转（Out-of-Plane Rotation）等问题。这些因素都会造成目标模型漂移甚至造成目标跟踪的失败，对跟踪算法的性能提出了很高的要求。

近年来，由于对跟踪算法的准确度和实时性提出了更高的要求，基于相关滤波的目标跟踪算法凭借其高效的计算效率和良好的跟踪性能引起了研究人员极大的关注。Bolme等[1]提出MOSSE算法，该算法首次将相关滤波引入目标跟踪领域。在计算目标和待测样本集之间相关性时，其通过傅里叶变换，直接将运算转换到频域中，大大降低运算量，提高了运算速度，跟踪速度甚至能达到每秒数百帧。随后，Henriques 等[2]在MOSSE 的基础上提出了采用循环矩阵结构和核空间映射的CSK方法。这种方法只需要在目标位置提取待测样本，然后利用循环偏移方式增加训练样本的数量，使训练结果更准确。2014年，Henriques等[3]在CSK的基础上提出核相关滤波KCF，该方法将CSK 单通道灰度特征扩展为基于HOG 多维特征，极大地提高了相关滤波目标跟踪的鲁棒性。虽然上述算法在跟踪速度和性能有很大的提高，但是当目标出现遮挡或者尺度变化时，在每帧都进行更新的情况下，会出现模型漂移从而影响跟踪性能。Danelljan 等[4]提出尺度空间判别跟踪方法DSST，采用单独的尺度滤波器来对目标的尺度变化进行判断从而解决尺度变化问题。Dong 等[5]通过构建分类池缓存以往模板。当出现重度遮挡时，通过选择最佳分类器进行重新检测来解决其中的遮挡问题。TLD[6]算法虽然引入检测模块，在判断跟踪目标丢失时对每一帧图片进行全局搜索来定位目标可能出现的位置。然而，这种方式有较大的盲目性计算效率不高，甚至无法得到较优的结果。Li等[7]提出了RPT跟踪算法，该算法利用蒙特卡罗框架估计置信度高的块分布，对部分遮挡比较有效，但是目标被长时间遮挡时很容易发生模型漂移问题从而导致跟踪失败。胡昭华等人[8]提出一种融合人工特征与深度特征目标跟踪方法，验证了双支路框架的可行性，提升了目标跟踪的效果。孙健等人[9]提出一种改进型的核相关滤波跟踪算法，用SVM 分类器检测目标。但是该方法没有提出在遮挡等情况下目标跟踪置信度问题，无法有效处理目标遮挡等情况。

刘芳等[10]提出基于深度特征的自适应模板更新算法去解决遮挡尺度变化等问题，取得了很好的跟踪效果，但是该方法采用卷积神经网络去提取目标特征，计算复杂度比较高，耗时严重。Sui 等[11]提出利用一种新的峰值强度来衡量相关滤波器的判别能力，很好地解决了由于遮挡和局部形变而导致的性能下降问题。

虽然以上跟踪算法针对目标跟踪过程中出现遮挡、形变等问题进行了改进取得了不错的跟踪效果[12-17]，但在跟踪过程中仍存在以下问题：一个问题是很多算法没有对跟踪结果进行可靠性的判定[18-19]，每一帧的结果都用来更新，或者每隔几帧更新一次。当目标出现被遮挡等情况时，利用不可靠的数据去更新模型，只会使得跟踪器越来越无法识别目标，造成模型漂移。另一个问题是当跟踪目标被遮挡、剧烈形变甚至丢失视野时，这些算法无法进行有效的重新检测，重新找到所跟踪的目标[20-23]。针对以上问题，本文提出了一种基于自适应更新策略和再检测技术的关联跟踪算法。通过自适应更新策略和再检测策略双重检测机制，提高了相关滤波跟踪结果的准确性和鲁棒性。

1 核相关滤波目标跟踪框架

本文采用核相关滤波目标跟踪框架，通过跟踪算法对所标定的目标区域进行训练得到滤波器更新模板。在目标的跟踪过程中利用相关性找到与滤波器模板相关度最高的位置标记为目标可能存在的位置。最后利用自适应更新策略和再检测策略对目标可能存在的位置进行置信度判断和对不可靠的位置进行重新定位。具体算法流程如图1所示。

步骤1训练目标跟踪模板。根据目标所在的矩形区域及背景样本提取目标特征，采用相关滤波方法训练目标滤波器模板，并估计目标在下一帧所在的新的位置。

步骤2目标尺度估计。在下一帧图像目标范围提取目标特征，构建目标金字塔，估计出最优尺度。

步骤3模板更新。采用自适应更新策略机制对目标响应峰值位置进行置信度判断并对模版进行自适应更新。

步骤4目标重新检测。构造在线SVM 检测器，当跟踪目标被长期遮挡或者在视野外发生跟踪失败等情况时，启动检测器对目标重新定位。

步骤5目标跟踪。循环步骤1～步骤4 直至跟踪结束。

2 核相关滤波架构

本文采用核相关滤波（KCF）架构，该算法的思想是通过对图像块进行循环密集采样构造循环矩阵，丰富目标样本。然后基于循环矩阵的特性，利用循环矩阵对角化，把对问题的求解变换到了离散傅里叶变换域。这一过程免了矩阵求逆问题，大大缩减计算复杂度，提高了训练速度，最终达到快速跟踪目标的目地。样本训练采用岭回归函数训练分类器，通过训练出的分类器对新输入的图像与前一帧图像进行相关性判断，目标响应峰值位置可认为就是所预测的目标可能存在的位置。样本训练过程实际上是一个岭回归问题，训练的目的就是找到函数f(z)=wTz，使得平方误差达到最小值，即：

核相关滤波器就是引入核函数，求解核空间的岭回归。通过非线性映射函数φ(x)，将特征空间映射到一个更高维的空间，使映射后的样本在新空间中线性可分。此时分类器特征向量为优化问题转化为求解向量α问题。引入核函数κ(xi,xj)，目标函数可表示为：

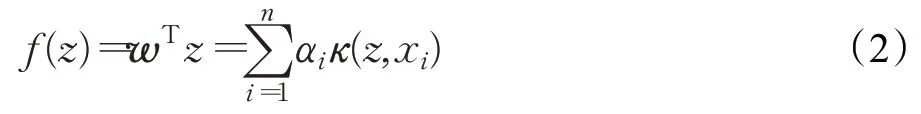
对式（1）求解得：

式中，K为构造循环矩阵，I为单位矩阵。

利用循环矩阵的性质，通过离散傅里叶变换对α进行求解得：

式中，α^ 为目标滤波器的参数，在傅里叶域中向量x与其自身的核相关性。

为对所追踪的目标进行快速追踪，确定当前帧目标的位置，引入核矩阵Kz=C(kxz)，对式（2）进行求解，并求傅里叶变换得：

式中，αt为采用插值更新后第t帧目标滤波器参数，xt为采用插值更新后第t帧模型的特征。η为模型更新插值。′为在第t帧所求目标滤波器参数，′为第t帧所求模型特征。

3 自适应模版更新策略

3.1 目标置信度判断

在实际的目标跟踪过程中，所跟踪目标的运动场景非常复杂并且经常发生变化。例如，目标的遮挡（Occlusion）、形变（Deformation）、快速运动（Fast Motion）等。想实现长时间稳定的跟踪，还面临很多的限制和挑战。在目标跟踪的过程中，如果不对每一帧数据的有效性进行判断就更新模版，当目标发生遮挡等情况时，目标模版会学习到错误的目标表征信息而引起模型漂移，进而导致跟踪失败。因此针对以上情况，制定一个有效的目标模版更新策略对目标跟踪结果进行评判是很有必要的。

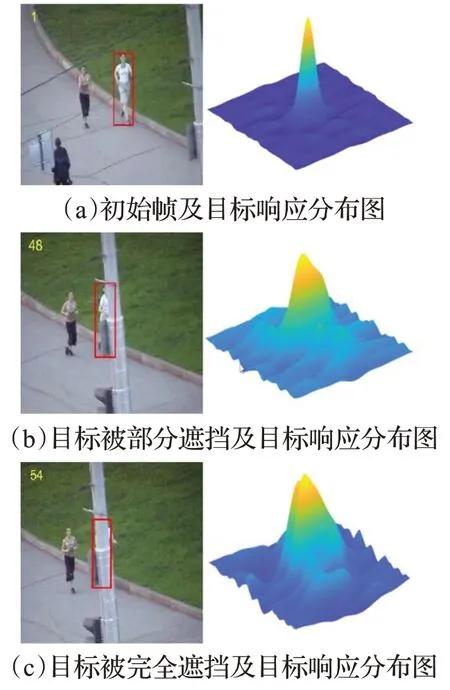
图2 目标在不同场景下跟踪响应分布

在目标跟踪的过程中，可以根据响应图的分布情况对所跟踪目标进行准确度判断，响应图的峰值越高说明跟踪的结果越好。如图2 所示，在图2（a）为目标在第1帧所处的位置和目标响应分布。当所跟踪的目标背景简单无遮挡时，目标跟踪准确，响应图为一个很明显的单峰并且响应分布接近理想的二维高斯分布图；图2（b）中，第48帧中的目标被部分遮挡，目标周围存在干扰物体。响应图开始出现震荡，峰值减小；图2（c）中，所跟踪的目标被完全遮挡，响应图出现多峰且峰值很小。如果按照最大峰值的位置为所跟踪的目标，在54 帧所跟踪的目标由于被遮挡而出现伪峰，峰值最大的位置不是目标所在的位置。如果只用这一个判据对模型进行更新，会因判断不准确而使模型漂移到被遮挡物体上，导致后续跟踪失败。

置信度判断依据两个指标：第一是响应图峰值Fmax大小；第二是响应图的波动情况APCE。用变量EAPCE表示平均峰值相关能量，如公式（7）所示：

式中，Fmax、Fmin为目标响应的最大值和最小值。Fw,h为目标在响应矩阵w行h列的值。如图3所示。

图3 目标在不同场景下跟踪响应置信度分布

如图3（a）所示，当目标正常跟踪时，目标响应最大值为Fmax=0.730 5并且平均峰值能量EAPCE=117.371 8很高，此时目标高度置信，可以对目标模版进行更新；在图3（b）中，目标被部分遮挡，目标响应最大值为Fmax=0.255 2降低，平均峰值能量EAPCE=10.751 6急剧减小。目标响应的波动很大时可以判断目标处于低置信度状态，目标模版参数保持不变防止模型漂移；在图3（c）中，目标被完全遮挡，目标响应最大值为Fmax=0.151 5 和平均峰值能量EAPCE=5.233 5 都很低，目标响应出现很多伪峰且持续震荡。Fmax和EAPCE这两个数据指标从局部和整体两个角度反映了目标跟踪置信度情况，因此可以根据这两个指标判断目标是否被遮挡。

在目标跟踪过程中，对目标是否被遮挡进行判断，采用自适应的更新策略对跟踪模版进行更新。本文通过对滤波器的响应设置阈值的策略对目标模版进行更新。在视频序列的第t帧中只有当目标跟踪置信度指标Fmax和EAPCE分别以一定比例超过自身的历史均值时，可以认定当前帧可置信。置信度阈值Tr为：

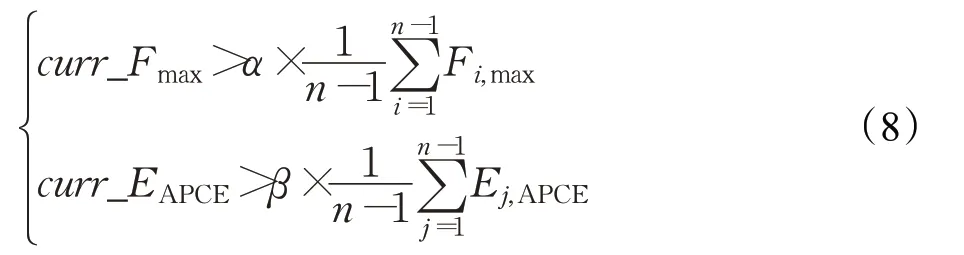
式中，α，β模版更新置信度参数。

目标跟踪过程中置信度策略如图4 所示，图中所示的是在Jogging 序列中所跟踪的目标从第30 帧到第70 帧状态的变化。目标从完全显示无遮挡到部分遮挡、完全遮挡再到完全显示在视野中几种运动状态的变化。

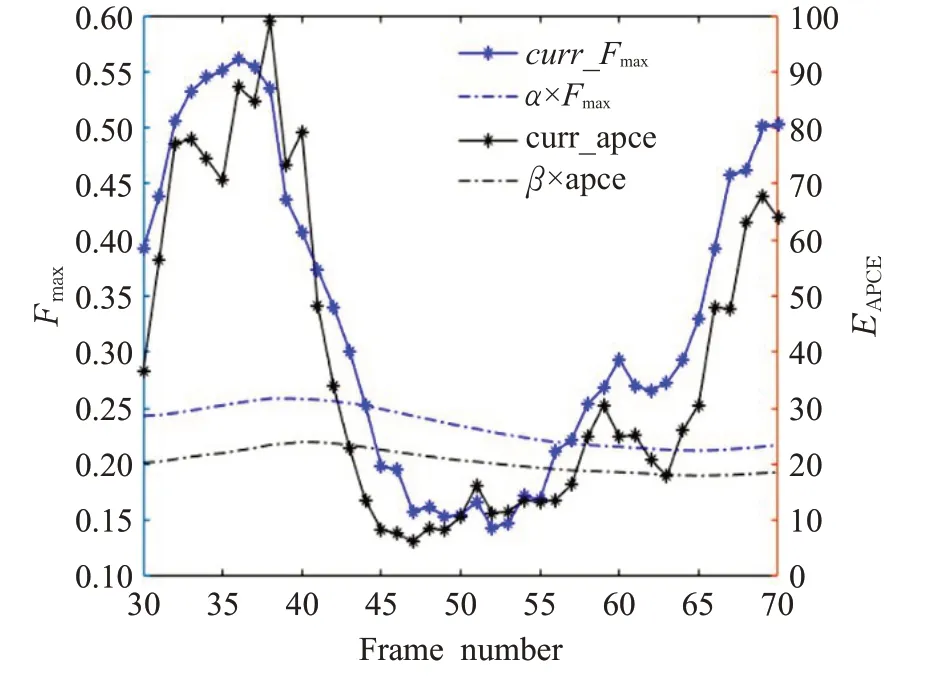
图4 在Jogging序列中目标跟踪置信度

在目标跟踪的过程中，依据目标跟踪置信度指标Fmax和EAPCE对所跟踪目标的置信度进行判断。目标响应峰值Fmax的历史均值与模版更新置信度参数α的乘积所得的曲线为目标响应峰值置信度曲线；平均峰值EAPCE的历史均值与模版更新置信度参数β的乘积所得的曲线为平均峰值波动置信度曲线。当目标响应的峰值处于目标响应峰值置信度曲线上方时，可认为当前峰值处于可置信状态；同理，当平均峰值EAPCE处于平均峰值波动置信度曲线上方时，可以认为当前帧的峰值波动情况可以接受，目标处于可置信状态。在图4 中，45～55帧这一区间处于低置信度状态，目标处于部分遮挡到完全遮挡这一状态中。实验所得结果与实际情况基本一致。在本算法中参数α=0.45,β=0.6。

3.2 目标模板自适应更新

在目标跟踪过程中需要对跟踪模版和SVM分类器进行自适应更新，以防止模型漂移。在本文中根据多种跟踪情况设置不同置信度区间，更新策略如下：

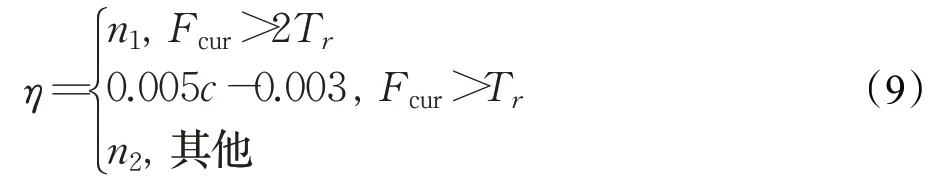
式中，c=0.5EAPCE+0.5Fmax，n1=0.05，目标处于高置信度状态，n2=0.01，启动SVM分类器进行检测。

目标跟踪过程中模板更新系数的变化如图5所示，图中所示的是在Jogging 序列中目标从第30 帧到第70帧状态的变化。在视频序列的第30 帧到第35 帧之间，所跟踪目标没有被遮挡。目标跟踪的置信度为所设定的阈值的2 倍，此时目标处于高置信度状态，以固定值n1更新滤波器模版与SVM分类器。在视频序列的第35帧到45帧之间，目标逐渐被遮挡，目标的跟踪置信度逐渐降低。当目标跟踪的置信度大于可信度阈值时，停止更新SVM分类器并地更新滤波器模版。在这一阶段动态调整跟踪过程中的模板更新系数，使滤波器模版具有更强的适应性。在视频序列的第45 帧到第60 帧之间，目标处于完全被遮挡状态，目标跟踪的置信度小于可置信度阈值。此时目标处于低置信度状态，启动SVM 分类器并以固定值n2更新滤波器模版，防止模型漂移。在视频序列的第60 帧之后，目标开始重新出现并根据目标的状态动态地调整模板更新系数，使其具有自适应能力。

图5 在Jogging序列中模板更新系数分布

4 跟踪判别及SVM再检测

在目标跟踪的过程中，由于目标外观变化、突然快速移动或者长时间被遮挡而出现所跟踪的目标丢失视野而导致跟踪失败。如图4 和图5 所示，在视频序列的第45帧到第60帧之间，此时目标被严重遮挡，目标的置信度很低。如果仍以比较高的模板更新系数对滤波器模板进行更新，可能会造成模型漂移甚至跟踪失败。因此，当目标处于低置信度状态时，滤波器模板以n1=0.01 的系数更新模板以保持模板的有效性。针对以上问题，本文提出当SVM再检测策略，即所跟踪的目标置信度低于所设定的可信度阈值Tr时，启动SVM检测器对所跟踪目标进行重新定位。在置信度高的帧中对所跟踪的目标及其周围的背景进行训练，得到密集的训练样本，并为这些样本特征向量分配标签。即，{(fi,ci)|i=1,2,…,N}。式中，f是样本的特征向量，c是标签ci∈{+1,-1} 。通过SVM检测器，对所跟踪目标的预测位置为中心密集地绘制样本，并对每个跟踪目标预测的位置进行打分，最后选择分值最大的图像位置为SVM 检测器预测位置。

SVM 分类器使用非线性映射方法，将分类问题转换为搜索最优超平面的问题。

分类平面可定义为：

在线性可分时：

在本文中偏置量b在第一帧用所求得为固定值。因此通过求解w值可得最佳分类平面。SVM分类器求得超平面满足下式：

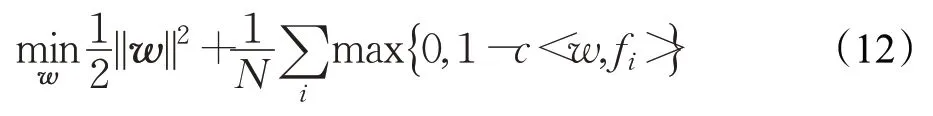
每个跟踪目标预测的位置得分可定义为：

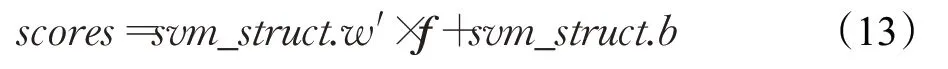
具体过程如图6所示。

图6 目标丢失检测器重新找到目标

在目标跟踪过程中，视频中的女子在经过柱子时，所跟踪的目标出现丢失。经过长时间的遮挡，滤波器学习到错误信息，置信度持续下降。在目标的置信度低于设定的阈值Tr时，启动SVM分类器进行重新检测。由于在相邻几帧图像中目标形状与位置一般不会发生太大的变化，因此目标中心搜索区域大小设定为上一帧目标外接框大小的2倍，并在此搜索范围内采用滑动窗口的方式在预测区域进行搜索。此方法避免在算法在整幅图像上进行盲目地搜索，提高了运算速度。在搜索的过程中，对每一个图像块进行特征提取的HOG 特征向量作为上式中f的值，通过式（13）对所有的候选区域进行打分，当分数为正时样本为正。最终获得的得分最高的阳性样本可作为目标检测器所寻找到的可靠位置，流程结束。

5 实验结果与分析

5.1 实验参数设置

本文的仿真实验均在CPU 为Intel 酷睿i5 主频2.5 GHz，内存8 GB计算机环境，编程环境为matlab2018a进行。为了充分验证本文所提算法的准确性和鲁棒性，本实验选择OTB2013[12]作为测试数据集。在OTB2013数据集中的跟踪目标都具有遮挡（Occlusion）、形变（Deformation）、快速运动（Fast Motion）、背景杂波（Background Clutters）、光照变化（Illumination Variation）、超出视野（Out-of-View）、平面内旋转（In-Plane Rotation）、平面外旋转（Out-of-Plane Rotation）等属性，可通过这些影响因素对所测试的目标跟踪算法的鲁棒性有一个更全面、可靠的评价。

为了直观地对本文中所提的目标跟踪算法进行评估，将本文的算法与近几年所提的几种主流的相关滤波跟踪算法进行对比实验。选取以下几种主流算法作为对比：KCF、DSST、TLD、MIL、Struck等5个目标跟踪算法。

5.2 跟踪算法评价指标

（1）目标跟踪中心误差（Precision Plot）

目标跟踪的精度的测算主要通过计算每一帧所预测的位置中心点与benchmark 中所标注的目标中心点之间的欧式距离。通过欧式距离的大小评估目标跟踪的精度，欧式距离越小，精度越高。

（2）目标跟踪成功率（Success Plot）

目标跟踪的成功率是对目标追踪算法所得的边界框与benchmark 中所给定的边界框重合率的计算。计算公式如下：

式中，Ra、Rb分别为目标跟踪算法所得边界框与数据集所给的真实的边界框。当某帧的OS大于所设定的阈值时，可认为目标被正确跟踪。一般阈值设置为0.5。

5.3 实验结果分析

5.3.1 定性分析

首先，对本文的算法与其他的算法在不同视频序列中进行定性分析。如图7 所示，图中显示了6 种跟踪算法在8个不同场景下跟踪效果。

图7 跟踪算法在复杂场景下跟踪效果对比

本文所提算法主要是为解决目标在被遮挡等复杂情况下重新定位目标的问题。为验证算法的有效性，从OTB 数据集选取suv、subway、jogging1、jogging2、david3、shaking、freeman4、coke 等视频序列进行测试，这些视频序列都包含目标被完全遮挡等复杂情况。具体跟踪效果如图7所示，在目标跟踪的过程中，由于本文所提算法对目标置信度进行判断，根据置信度自适应地对目标模板进行更新。当目标被完全遮挡又重新出现后，能迅速找到目标位置进行重新定位。具体分析如下：

（1）超出视野：在视频序列suv 中，汽车在前进的过程中出现超出视野和遮挡等情况，如图7（a）所示。文中所提的方法相比于其他方法表现出更好的适应能力，能更迅速准确地找到目标。

（2）背景杂波：以视频序列subway 为参考，如图7（b）所示。在所跟踪的目标附近，背景具有与目标相似的颜色或纹理，目标在运动中会出现部分遮挡的情况。由于目标所处的环境比较复杂，这对算法的性能提出了更高的要求。文中对所跟踪目标进行置信度判断，有效减少因背景产生的错误信息，并将其更新到目标模型中。因此始终能准确地跟踪目标。

（3）目标遮挡：在视频序列jogging1、jogging2、freeman4、coke 中，如图7（c）、（d）、（g）、（h）所示。两组jogging视频序列中行人在跑步的过程中被柱子完全遮挡，目标丢失。本文所提算法在行人经过柱子前，对目标进行置信度判断，当目标丢失启动再检测模块，目标重新出现以后可以迅速地找到目标。在freeman4 序列和coke序列均出现目标被完全遮挡情况，其余算法在目标丢失后发生漂移，甚至丢失目标。本文算法对遮挡情况具有较好的鲁棒性，能始终正确跟踪目标。

（4）形变：以视频序列david3 为例，如图7（e）所示。目标在步行过程中被部分遮挡，此时运动目标发生转身等姿态变化。对比不同算法结果，本文所提的方法能对跟踪目标状态的变化进行准确地跟踪，其他算法出现了不同程度地漂移。

（5）光照变化：以视频序列shaking 为例，如图7（f）所示，检测算法在光照发生变化时的跟踪能力。视频序列中光照变化来自于后面灯光的变化，在视频序列中大部分的算法都发生了漂移等问题，但在后续的视频帧中，当光照逐渐增强时本文所提的算法可以持续稳定地进行跟踪。

5.3.2 定量分析

本文主要采用目标跟踪中心误差，目标跟踪成功率作为评价标准来检测不同算法在不同场景下的跟踪性能。图8 为算法在OTB2013 目标跟踪数据集上所有的跟踪结果的综合评价。

图8 综合评价指标对比结果

对比各算法在数据集上精度和成功率这两项指标可以发现，本文所提的算法在目标跟踪精度上较KCF提高13.3%，较DSST提高13.8%。在目标跟踪的成功率上本文算法较KCF提高17.4%，较DSST提高8.8%。

表1、表2 为6 种跟踪算法在不同的跟踪环境条件下跟踪性能的比较。跟踪环境包括：遮挡（Occlusion）、形变（Deformation）、快速运动（Fast Motion）、背景杂波（Background Clutters）、光照变化（Illumination Variation）、超出视野（Out-of-View）、平面内旋转（In-Plane Rotation）、平面外旋转（Out-of-Plane Rotation）。由表1 与表2 中的数据分析可知，本文所提的算法与其他算法相比，本文所提算法在大部分的跟踪环境下为最优结果。

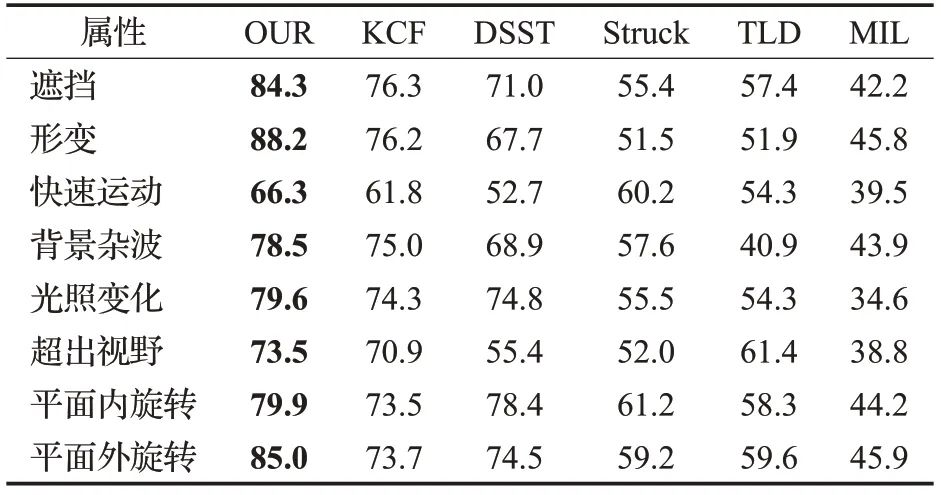
表1 算法精度跟踪性能对比 %

表2 算法成功率跟踪性能对比%

5.3.3 复杂度分析

在自适应更新策略阶段，在对跟踪目标响应峰值的波动情况进行分析时，平均峰值相关能量EAPCE时耗费的时间复杂度为O(n2)。在再检测阶段，使用SVM分类器去寻找最优解。当训练样本的个数为n时，对于一个测试样本标准支持向量机的时间复杂度是O(n3)。在本文中基于自适应更新策略和再检测技术算法所需的时间复杂度为：

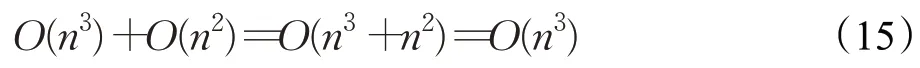
由式（15）可知，本文所提的算法时间主要消耗在寻找最优解的步骤中。虽然跟KCF算法相比本文所提算法速度为20.4 帧/s，在速度上有所降低。但在目标跟踪精度上较KCF提高13.3%，在目标跟踪的成功率上本文算法较KCF 提高17.4%。与KCF 算法相比性能上有较大的提升，并且能满足实时跟踪的要求，在OTB数据集上显示，本文所提算法具有良好的跟踪性能。

6 结论

本文提出了一种基于自适应更新策略和再检测技术的关联跟踪算法对目标进行实时跟踪。利用目标响应峰值和平均峰值的波动情况，对目标响应峰值进行置信度的判断。根据所提的自适应更新策略动态调整滤波器模版更新系数，对目标跟踪模版进行更新。当判断目标此时处于低置信度状态时，用再检测模块对低置信度的位置进行重新检测，重新选择出最优的预测位置。通过实验表明本文所提算法在目标被遮挡或目标外观发生突变时，能实现对目标跟踪模版的自适应判断和更新。在目标被严重遮挡时可对目标进行重新检测并寻找到目标，可有效解决在长时间的跟踪过程中目标被遮挡、丢失视野等问题。