基于联合分布的多标记迁移学习

桑江徽，姜海燕

南京农业大学 信息科技学院，南京210095

多标记数据普遍存在于现实世界中并得到了广泛的研究，如面部表情识别、情感分析等。多标记机器学习的巨大成功通常取决于大量有标记信息的训练样本。但是，具有多标记信息的样本不易获得，且人工标注工作费时费力且精度难以得到保障，因此多标记迁移学习应运而生。多标记迁移学习常用于解决多标记样本稀缺的问题[1-3]，它放宽了经典机器学习关于训练样本和测试样本必须服从独立同分布这一重要的基本假设[4]。多标记迁移学习的核心思路是通过缩小领域之间数据的分布差异从而实现数据复用。数据分布由边际分布和条件分布组成，其中边际分布反映了领域之间数据整体相似性，缩小领域间的边际分布差异能够使得源领域的整体特征更加有效地训练目标领域模型（如图1（a）→（b））；而条件分布则反映了领域间每种类别的差异性，缩小条件分布差异可进一步刻划领域间的特征信息（如图1（a）→（c））。

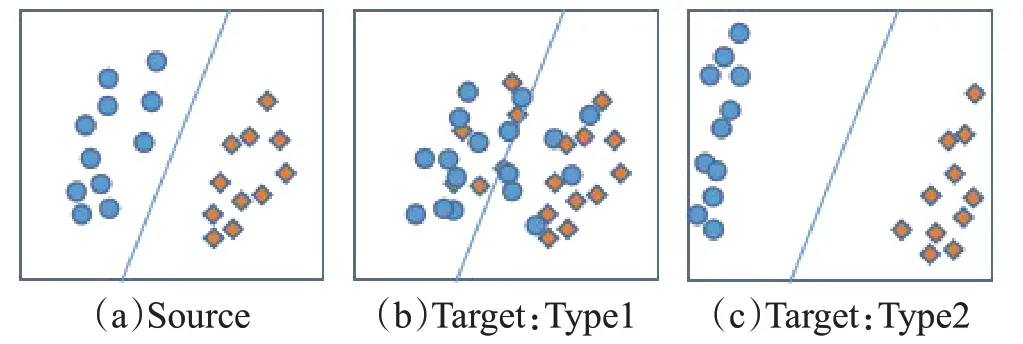
图1 不同领域样本数据的分布

现有的多标记学习方法在缩小领域间分布差异时更多地考虑数据的边际分布[5-8]。例如，Multi-Label Transfer Learning with Sparse Representation（S-MLTL）[5]为了解决多标记图像样本稀缺导致的模型训练困难，首次提出了多标记迁移学习，使用多标记稀疏编码将数据嵌入特征子空间中，使得共享标签的样本在子空间中彼此接近，子空间中的新特征表示更具有判别力。但是，S-MLTL仅仅考虑了多标记之间的关系，并没有缩小领域间的边际分布，因此在子空间中源领域特征和目标领域特征仍然存在较大的差异。针对目标领域与源领域整体差异性过大带来的适配难题，基于最大均值差异的多标记迁移学习算法（Multi-label Transfer Learning via Maximum Mean Discrepancy，M-MLTL）[6]在子空间中引入了最大均值差异（Maximum Mean Discrepancy，MMD），有效地缩小领域间的边际分布差异，提升分类精度。但是，M-MLTL 仅仅考虑了数据的边际分布，忽略了条件分布，在领域间整体差异较大时能够取得良好效果，但难以适用于领域间整体差异较小、类别差异较大的情况。近些年，多标记迁移学习同样解决了深度学习中样本稀缺的问题[7-8]，Zhuang[7]提出了多标记深度迁移网络（Transfer learning Network，TNet），利用卷积层提取目标领域样本的深度特征，辅助源领域网络模型的构建，但TNet 在多标记迁移时也仅考虑了数据的边际概率分布，忽略了条件概率分布。

现有的多标记学习在缩小领域间分布差异时仅仅考虑了数据的边际分布，当源领域和目标领域整体存在较大差异时，缩小边际分布差异能够有效地提升算法性能；但是当目标领域和源领域整体较为相似时，边际分布对数据的抽象拟合能力不足，无法充分反映跨领域数据的真实特性，导致算法在此类情况下效果不佳，即现有算法的泛化性能不足。

当目标领域和源领域整体较为相似时，多标记迁移学习应该关注跨领域数据的条件分布，度量条件分布可以进一步缩小领域间的差异性。针对现有算法忽略数据的条件分布而导致的泛化能力较差的问题，本文提出一种基于联合分布的多标记迁移算法（Multi-label Transfer Learning based on Joint Distribution Adaptation，JMLTL）。J-MLTL同时度量领域间的边际分布和条件分布，当数据整体差异较大时，边际分布会发挥较大作用，当数据整体相似时，条件分布会发挥较大作用。J-MLTL利用非负矩阵三分解（Non-negative Matrix Three Factorization，NMTF）将源领域和目标领域特征映射到子空间，在子空间中根据样本全局结构特征学习多个标记的“重要性”信息，并计算每个类别对应的条件分布的权重系数，“重要性”较大的类别被分配较大的权值，反之被分配较小的权值，通过缩小条件分布差异来进一步缩小领域间的差异，提升算法在领域间整体相似的情况下迁移效果。此外，J-MLTL 利用超图（Hypergraph）来描述多标记数据的几何结构信息，Hypergraph的超边将具有相同标记的样本进行连接，加强了数据在流形空间中的联系，有利于强化迁移效果。

1 基于联合分布的多标记迁移算法

为方便表述，表1中给出了本文常使的符号及相关含义。

表1 本文中常用符号及描述

1.1 联合分布适配

J-MLTL 旨在通过边际分布P 和条件分布Q 来缩小领域间差异。当源领域数据X(s)和目标领域X(t)整体之间存在很大差异时，缩小边际分布Ps和Pt之间的差异有利于提升迁移效果。当数据集整体相似时，此时缩小Qs和Qt条件分布差异更为重要。值得注意的是，相比于单标记数据，多标记数据包含更加丰富的类别信息。鉴于这种现象，本文提出一种基于多标记数据的联合分布

源领域X(s)和目标领域X(t)的条件分布的MMD距离被定义为：

1.2 类别权重θ 的定量计算

值得注意的是，多标记数据同时含有多个标记，但是多个标记的所含信息的重要程度不同。在图2 所示多标记迁移时，“山”“海”“天空”“沙滩”标记更能表达图片内容，而“建筑”和“人”对图片内容贡献较小，此时前者标记应该被赋予更大的权重，后者标记应被赋予较小的权重。

图2 迁移学习中的多标记图像

本文根据跨领域样本特征的全局结构学习标记重要性，再根据标记重要性学习θ。针对第i个样本xi，算法构造d×(n-1) 维的全局特征矩阵Xˉi=[x1,x2,…,xi-1,xi+1,…,xn]。在典型稀疏表示下，xi的编码向量αi可通过求解如下优化问题获得：

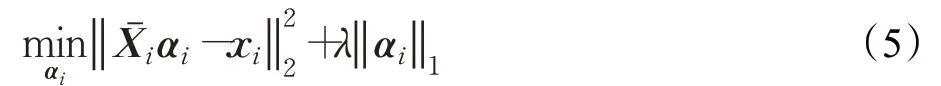
稀疏表示的权重矩阵Zn×n可由编码向量αi和零对角元素构造。假设特征空间中的结构关系也在标记空间中存在，那么利用Z中编码的结构信息来生成丰富的标签信息矩阵{β1},β2,…,βi,…,βn，则样本xi对应的标记信息向量βi可通过如下优化问题获得：

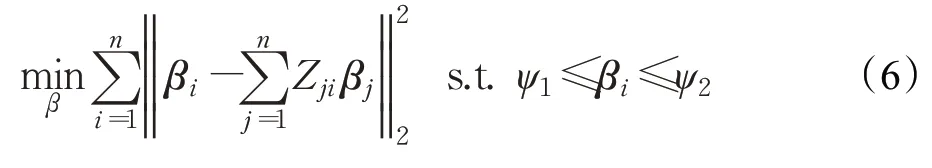
ψ1和ψ2是βi的取值范围约束。显然，式（6）是一个标准的二次规划（Quadratic Programming，QP）问题，可以通过已有的QP 工具箱进行求解。在求解βi后，θ由式（7）可得：

其中，ξ(·)是标记信息到类别的映射关系。

1.3 流形正则

由文献[11]可知，数据的统计信息和几何结构通常从不同方面刻划了数据分布，因而在描述数据特性方面具有相互强化的效果。算法使用MMD 从统计信息方面刻划了数据分布，同时利用超图[12]从几何结构对数据进行描述，提高样本间几何关系表达的效率和可靠性，同时保持领域内几何流形结构不受领域外知识结构的影响，提高特征结构的迁移能力，有效地加强了标记之间的联系，有利于强化迁移效果。

超图拉普拉斯学习有若干种方法，如：团体扩展方法、星型扩展方法、波拉拉普拉斯等。本文采用文献[13]提出的归一化超图拉普拉斯算子：

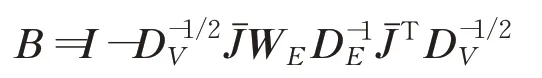
1.4 目标函数

迁移学习的一个主要方法就是基于特征映射的方法，将各个领域的数据从高维特征空间映射到低维特征空间，在该低维空间下，源领域和目标领域的数据拥有相同的分布，这样就可以利用低维空间表示的有标签数据样本训练分类器。

受到数据自我表示的启发，基于字典学习和矩阵分解的方法有利于揭示原始数据的全局结构。J-MLTL对跨领域特征X=[X(s),X(t)]进行非负矩阵三分解，并将原始数据X视为字典。因此，J-MLTL的目标函数f如下：

为了强化特征子空间中多标记样本之间的空间结构，进一步强化迁移效果，算法将超图正则项加入目标函数中，通过流形学习保持领域内几何结构信息不受领域外知识结构破坏。超图的超边连接了具有相同标记的多个样本，保证了标记间信息不损失。超图正则项可以形式化为：

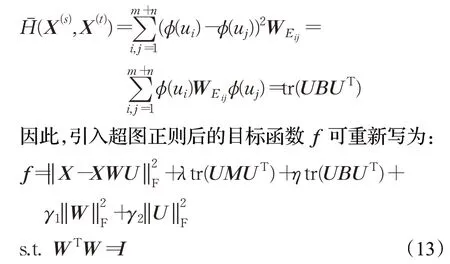
其中，η是用于控制超图正则项的非负系数。

1.5 优化

式（13）可以利用交替迭代法进行求解，具体求解过程如下：

步骤1固定U求解W。f是关于W的函数，其余项可视为常数，则目标函数f可简单表示为：

所有的矩阵变量都是采用正态分布随机数矩阵初始化，然后利用交替迭代法来求局部最优解。经上述分析，基于联合分布的多标记迁移学习算法详细步骤如下：

输入：原始数据矩阵X，正则项参数λ、η，潜在特征维数k

输出：子空间特征矩阵U

步骤11.根据等式（5）～（7）计算权重系数μ

2.根据等式（10）、（11）计算MMD矩阵M

3.初始化矩阵W和U

步骤2求解优化问题（13）

Repeat

1.根据式（14）、（15）并利用curvilinear 搜索方法

更新W

2.根据式（16）并利用Bartels-Stewart算法更新UUntil 符合停止标准

2 实验设置

本章主要介绍用于实验研究的基准数据集、对比算法和评价指标。

2.1 多标记迁移数据集

本研究采用已经被广泛认可的图像数据集Corel5k、ESPGame和Iaprtc12。表2给出了3个数据集的统计信息。

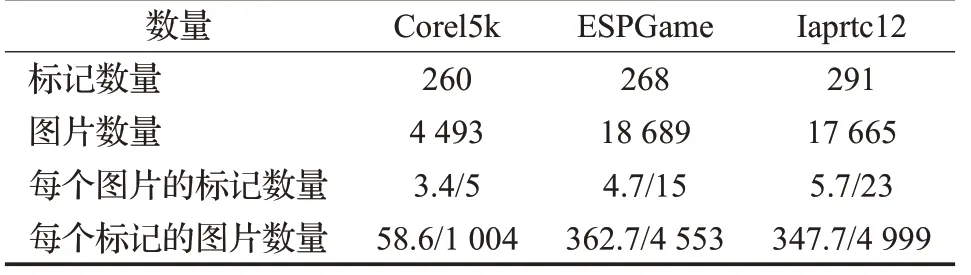
表2 多标记数据集的统计信息（均值/最大值）

（1）Corel5k 数据集是Corel 公司收集整理的5 000幅图片，可以用于科学图像实验：分类、检索等。它包含了5 000 张图像和260 个类别关键字，每张图像被手工标注1～5个关键字。

（2）ESPGame原本是一款在线游戏，这款有趣的游戏鼓励众多玩家参与数据标记工作。不同玩家对图片进行单词标记操作，如果单词名称相同，则他们可以获得奖励积分。ESPGame 数据集包含的图像比Corel5k更多样，除了照片还包括商标、涂鸦等类型的图像。

（3）Iaprtc12 基准测试的图像采集包括从世界各地拍摄的20 000 张自然图像，包括各种横截面的静止图像。这包括不同运动和动作的照片，人物、动物、城市、风景和当代生活的许多其他方面的照片。

2.2 特征提取与多标记

本文对上述多标记图片提取SIFT特征。SIFT是图像处理领域中经常使用的局部特征描述方法，基于物体上某些局部外观的兴趣点进行特征提取。SIFT特征具有比例不变性，与图像的大小和旋转无关，同时SIFT对光线、噪声和微视角变化也具有很高的鲁棒性。此外，SIFT 提取特征速率较高，适用于海量数据库中的快速准确匹配。

实验设置多标记为“mountain”“sky”“sun”“water”，源领域样本数量设置为800，目标领域样本数量设置为200。将上述3个基准数据集分别交替作为源领域和目标领域，最终构造6个多标记迁移学习数据集“Corel5k→ESPGame”“ESPGame→Corel5k”“ESPGame→Iaprtc12”“Iaprtc12→ESPGame”“Corel5k→Iaprtc12”和“Iaprtc12→Corel5k”。数据集的信息如表3所示。

表3 本文构造的数据集信息

2.3 对比算法

本文实验使用以下3 种对比算法：S-MLTL[5]、MMLTL[6]、TNet[7]。

（1）TNet（Transfer learning Network）是无监督深度迁移学习算法，通过卷积层提取源领域和目标领域图片的深度特征，并利用MK-MMD度量领域间深度特征的边际分布差异。

（2）M-MLTL（Multi-label Transfer Learning via Maximum Mean Discrepancy）使用子空间学习，分解“特征-标签”矩阵G来获取源域和目标域的新特征表示。此外，M-MLTL使用MMD来度量并最小化子空间中的新特征UXs和UXt的差异。最后，M-MLTL 使用新特征UXs训练RankSVM 并预测特征UXt的标记。此算法仅考虑边际分布而忽略了条件分布，同样忽略了多个标记之间的关系。

（3）S-MLTL（Multi-Label Transfer Learning with Sparse Representation）考虑了多个标签之间的内在关系，并将Hypergraph用于空间流形约束以获取稀疏表示。该算法通过稀疏线性嵌入将目标数据映射到新的特征空间。S-MLTL 使用源领域的稀疏表征来训练RankSVM并预测目标域样本。与上述方法不同的是，S-MLTL考虑多个标签之间的关系，却没有考虑数据分布。

2.4 分类器

实验采用Ranking Support Vector Machine（RankSVM）[16]作为分类器，RankSVM 是一个针对多标记数据的分类器，利用L个线性分类器R={(Ri,bi)|1＜j ＜L}来构造超平面。其中，第i个线性分类器ri采用empirical ranking loss来判断第i个标记yi。

2.5 评价指标

本实验使用广泛使用的4种基于样本的多标记评价指标和一种基于标记的多标记评价指标[15]：Hamming Loss、Ranking Loss、One-Error、Coverage、Average Precision。前4 个评价指标的值越小，性能越优；最后1 个评价指标的值越大，性能越优。实验运行LC-MLTL 与上述的对比算法总共3次，考察各个评价指标的均值。

（1）Hamming Loss

衡量在测试集上遍历到样本所有相关标记的平均查找深度。

（5）Average Precision

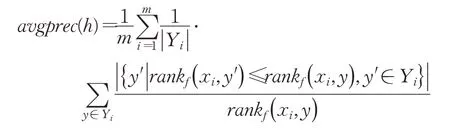
考察在样本的标记排序序列中，排在该样本相关标记之前的标记仍为相关标记的比例。

3 实验结果和分析

实验在上述多标记数据集上运行3次J-MLTL和对比算法，并在下列实验中显示评价指标的均值。实验主要分析各个算法的精度对比、分布类型对迁移的影响、标记关系对迁移的影响以及算法耗时分析。

3.1 精度分析

本节实验通过对比J-MLTL 算法和其他算法在6个迁移数据集上的表现来考察算法的分类性能。为了直观地观察结果，本实验计算5 个评价指标在6 个迁移数据集上的均值，结果如表4 所示，较优的结果被加粗表示。

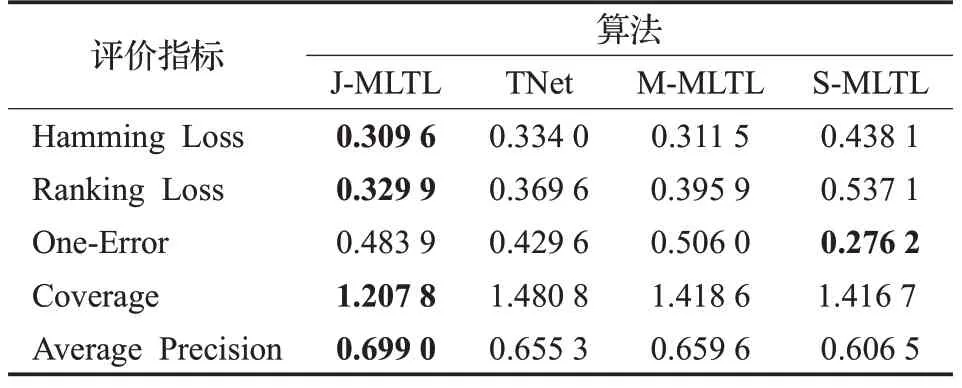
表4 各算法的分类结果（均值）

观察Ranking Loss 和Coverage 指标，J-MLTL 与对比算法有着明显的优势，J-MLTL 出现更少的标记排序错误同时查找深度较小，说明J-MLTL 在多标记关系的处理上优于其他算法。因为Hypergraph 利用超边将相同标记的样本连接起来，加强了迁移过程中具有相同标记的样本之间的联系。J-MLTL 的Average Precision 分别高于TNet约4.5%、M-MLTL约4%、S-MLTL约9%，因为J-MLTL 在迁移时考虑了多标记数据的条件分布，相比于仅考虑边际分布的M-MLTL 和TNet，本文所提算法更适用于源领域和目标领域整体相似的情况。值得注意的是，J-MLTL的One-Error指标不佳说明在分类时部分样本的预测标记不在真实标记集中，这由于错误分类而导致的。因为特征子空间是通过原始特征的非负矩阵三分解生成的，新特征表示能力还有待提高。接下来的研究工作是加强子空间中特征的表示能力，减少错误预测标记出现的次数。

M-MLTL 普遍优于S-MLTL 说明边际分布能够反映领域间的整体差异，缩小边际分布能够有效地实现源领域数据在目标领域的复用。J-MLTL的各个指标均优于M-MLTL，而M-MLTL仅仅通过边际分布缩小领域间分布差异，因为本文所提出的多标记数据的联合分布适配起到了决定性因素，它能够根据多标记的“重要性”调整不同类别的条件分布的权重系数，使得源领域数据更加接近目标领域，进一步缩小不同领域在特征子空间的分布差异，提升迁移效果。

3.2 分布类型对迁移的影响

为了讨论本文所提的联合分布对迁移效果的影响，本实验设置了J-MLTL 与三组对比算法进行验证：J-MLTL1、J-MLTL2、J-MLTL3。其中，J-MLTL1目标函数的框架与本文所提出的J-MLTL 完全一致，但只考虑了数据的边际分布差异，即使用了经典MMD 进行度量；与之类似，J-MLTL2目标函数的框架也与J-MLTL 完全相同，使用了文献[17]所提出方法，同时考虑了数据的边际分布和条件分布，且两者权重固定1∶1，但是并没有考虑多标记的“重要性”，即θc=1；J-MLTL3将多标记数据看作一个“整体”，使用了文献[10]所提出的动态分布适配的方法，该方法动态调整边际分布和条件分布的相对重要性，但没有考虑多标记数据特性，忽略了标记关系信息。本实验仅考察上述算法在6 个迁移数据集上的各个评价指标的均值，结果如表5所示。

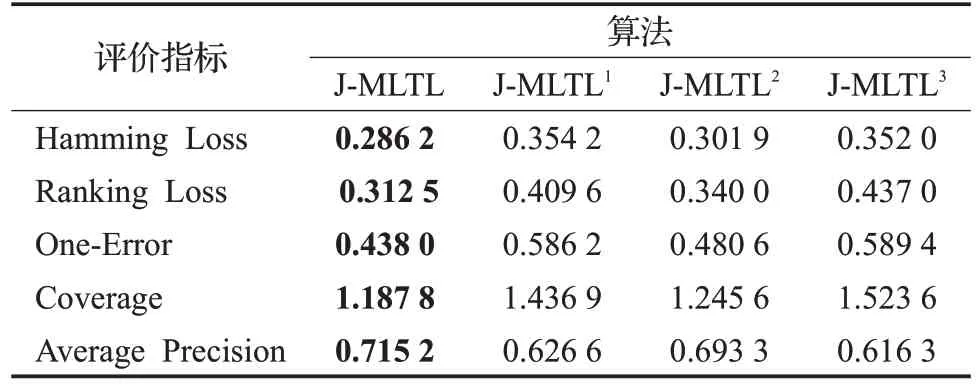
表5 不同的分布度量方法对迁移的影响

总体来看，J-MLTL 在各个评价指标上均取得了最佳成绩，体现了本文提出的多标记数据的联合分布适配的有效性。因为在不同图片样本中，每个类别标记所含的信息不同，挖掘出能够明显表达图片内容的“重要”标记将会对迁移起到积极作用。当源领域与目标领域整体差异较大时，算法应该更加注重缩小领域间的边际分布差异，而当领域间整体差异较小时，算法则应该关注条件分布差异。

从表5 可知，J-MLTL2＞J-MLTL1，说明文献[13]所提出的边际分布与条件分布的权重1∶1 的联合分布度量方法优于仅考虑边际分布的度量方法，尽管两者的泛化能力均不足，但加入了条件分布的度量方法更具有优势。J-MLTL3的各个指标均最低，虽然J-MLTL3动态地调整了条件分布与边际分布之间的相对重要性，但是它并没有考虑到多标记数据的特性，简单地将相同的多个标记看成一类“整体”会出现标记组合爆炸问题，导致目标领域和源领域样本的分布不平衡，每个类别的样本数量减少，最终会造成模型的学习困难。J-MLTL2与JMLTL的实验结果相近，因为在此实验中源领域和目标领域的各个类别的θc值在1左右浮动，并未起到较大作用，但是从整体来看，J-MLTL的评价指标略优说明强化重要、抑制非重要的标记能够提升迁移效果。

3.3 标记关系对迁移的影响

超图对相同标记的样本进行连接，加强了相同标记样本在几何空间中的联系。从几何结构对数据进行描述，提高样本间几何关系表达的效率和可靠性，同时保持领域内几何流形结构不受领域外知识结构的影响，提高特征结构的迁移能力。为了验证超图在迁移学习中起到的作用，本节实验设计了一组有无超图的对比算法（即J-MLTL、J-MLTL4）。其中，J-MLTL4在J-MLTL的基础上将超图正则项系数η置为0，使得超图在迁移过程中不起作用。实验结果如表6所示。

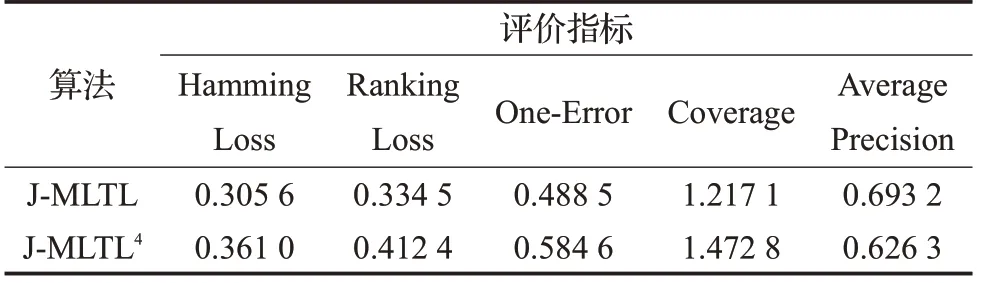
表6 超图对分类精度的影响

由表6 可知，J-MLTL 的Hamming Loss、Ranking Loss、One-Error、Coverage、Average Precision 评价指标分别优于J-MLTL4大约6%、8%、10%、26%、7%，说明算法在错误分类、错误标记排序和标记查找深度方面均有较大的提升。因为当原始特征被映射到子空间中，数据的几何结构信息会发生改变，超图能够将相同标记样本在子空间中连接，加强样本间的空间结构信息。J-MLTL4在学习时仅考虑了数据的统计信息，所以迁移效果不佳。J-MLTL 在构造子空间时，同时考虑了统计信息和几何结构，两者在描述数据特性方面具有相互强化的效果，最终的子空间特征U具有较好的表示能力。

3.4 算法耗时分析

算法的运行速度也是一个评价算法性能的指标。为了验证算法在运行速度上的表现，本节实验记录J-MLTL与对比算法（M-MLTL、TNet、S-MLTL、J-MLTL4）的运行时间。实验环境为CPU：Intel Xeon E5-2670 V3，内存：512 GB，GPU：NVIDIA GeForce GTX TITAN V，其中TNet使用了GPU加速。实验结果如表7所示。

表7 算法的耗时统计

由表7可知，S-MLTL算法运行一次所需时间最短，仅为8.17 s；TNet由于是深度多标记迁移学习，耗时最长；而本文提出的J-MLTL运行一次需要时间5 359.03 s，相比于传统的迁移学习方法，J-MLTL是耗时最多的算法，由此可知，J-MLTL提升精度的代价是大量计算。J-MLTL、J-MLTL4和M-MLTL耗时均较长，因为三者都是利用了矩阵分解技术进行子空间学习，并使用交替迭代计算方法优化目标函数，算法的耗时随着迭代次数的增加而增加。

值得注意的是，J-MLTL4耗时约是M-MLTL的9倍，这说明计算类别“重要性”环节消耗了大量时间，θ的计算实质上由两个优化问题构成：稀疏表示和二次规划问题。众所周知，两个优化问题的求解均需要大量的计算。J-MLTL 耗时约是J-MLTL4的两倍，说明超图学习所用时间较多，超图根据多标记将同类样本进行连接，在加强数据几何结构的同时产生了巨大的计算量，耗时随着样本数量、标记数量的增加而增加，这是导致J-MLTL 运行速率较慢的另一个重要原因。因此，提升J-MLTL运行速率是一个重要研究点。

4 总结

现有多标记迁移学习算法仅仅考虑了数据的边际分布，导致其在目标领域和源领域整体相似的场景下无法适用。为了解决现有算法适用范围受限的问题，本文提出了一种基于联合分布的多标记迁移算法J-MLTL，同时从概率分布角度和几何结构角度对跨领域数据进行刻划。J-MLTL 对原始特征进行非负矩阵三分解获得子空间中的潜在特征表示，利用稀疏表示方法学习特征的全局结构信息，并计算每种类别对应的条件分布的权重系数，通过调整条件分布的权重系数，使得源领域和目标领域数据的边际分布和条件分布差异进一步缩小。在此基础上，J-MLTL 考虑了多标记数据的几何结构信息，引入超图学习对数据进行描述，加强了具有相同标记的样本在流形空间的联系，提升了迁移效果。

但是，J-MLTL 在拥有较高的迁移性能的同时仍然存在不足：过大的计算量导致算法耗时过长。类别权重θ的定量计算实质上由两个优化问题构成，此环节使用最小二乘法和二次规划算法进行求解，由于本文使用了传统的优化方法，计算效率较低。此外，J-MLTL为了防止多个标记之间的信息损失，利用超图的超边将相同多标记的样本进行连接，因为超图学习的耗时较长，导致本算法在运行效率上低于现有算法。因此，下一步的研究重点是如何提升算法的运行速率。