薄膜在流延辊上冷却过程温度场的数值模拟研究

张 宏， 李陈晨， 战东毅

(大连理工大学机械工程学院，辽宁大连 116024)

引言

流延法是一种薄膜的主要生产方法，其过程为：原材料经过挤出机加热熔融，聚合物熔体经过模头挤出，流延到流延辊上迅速冷却成铸片薄膜，再经过测厚、电晕处理、牵引、切边等工艺，最后收卷成薄膜产品[1]，工艺流程如图1所示，其中，流延辊是薄膜生产过程中的关键部件，作用是将模头挤出的聚合物熔体迅速冷却成薄膜产品。薄膜的内部结晶情况、平整度及表面应力的分布与冷却过程有着密切的关系，直接影响膜片的质量与性能，而流延辊的结构参数直接影响着流延膜的冷却质量。因此，对膜片冷却过程的分析，以及流延辊结构参数的变化及控制，就显得尤为重要。合理布置流延辊的结构尺寸，研究薄膜在流延辊上冷却机理，这对提高薄膜的表面质量和力学性能以及指导现场生产有重要意义[2]。

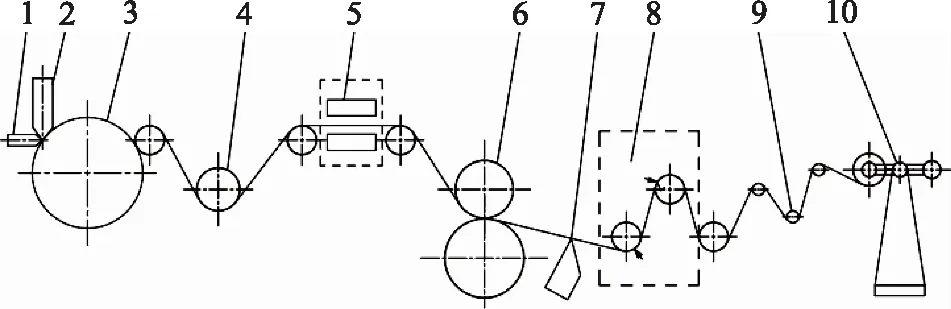
1.机头 2.气刀 3.流延辊 4.冷却辊 5.测厚仪 6.牵引辊7.切边装置 8.电晕处理装置 9.弧形辊 10.收卷装置图1 流延法薄膜生产工艺流程

目前，有国内外的一些学者对流延辊及流延膜的冷却机理进行了相关的研究。殷术贵等[3-4]通过对单向螺旋流道流延辊内部冷却水的流动情况的数值模拟，得到了辊内部冷却水的流动规律和性能，并对流延辊结构进行了优化。周喜灵等[5]对现有的螺旋流道结构的流延辊进行了温度场的数值模拟，得到了流道辊的温度场、辊筒内流体速率及温度场等，并对流道结构进行了优化。郭茜等[6]通过对平板流铸工艺中冷却辊的温度场的数值模拟，得到了冷却辊的温度场及其热流的分布特点，并探讨了辊直径、辊厚及辊速对辊表面温度的影响规律。吴哲浩等[7-8]通过对平行流道流延辊的数值模拟，得到了不同冷却水雷诺数、不同温度、不同流延膜厚度以及不同流延辊转速条件下流延膜的温度场。HUAWEI Z等[9]对单向螺旋流道流延辊进行了数值模拟，针对改善流延辊入口压力和出口压力提出结构优化。YONGKANG L等[10]对平面流延过程中的冷却辊进行了数值模拟，得到冷却水的流动特性以及不同辊筒转速下辊壁的温度和压力分布。

本研究采用双进双出螺旋流道流延辊模型，对膜片在流延辊上的冷却过程进行数值模拟研究，研究流延辊的多个结构参数对流延膜冷却效率及冷却后膜片表面温度均匀性的影响，并对流延辊的结构尺寸进行优化，为流延辊的结构参数的合理设置提供理论依据。

1 计算模型

1.1 物理模型及结构参数

本研究所采用的模型为双进双出螺旋流道流延辊，流延辊装配体由内辊筒、外辊筒、内套、导流片以及端盖构成，如图2所示。流延辊内部进出水流动示意图如图3所示。流道截面设置为矩形，共设置10个导流片，冷却水通过进水口后分成两部分，一部分流入左端盖的进水腔内，导入5个导流片内正向流动，最终由右端盖的出水腔及出水口流出；另一部分的冷却水则通过内辊筒流入右端盖的进水腔内，导入另外5个导流片中进行反向流动，由左端盖的出水腔流出，进入外辊筒，最终由出水口流出。这样的结构实现了冷却水的交错流动，大大提高了冷却效率及流延辊表面的温度均匀性。

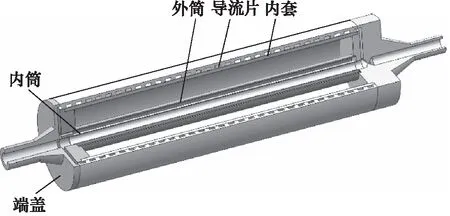
图2 螺旋流道流延辊结构图

图3 流延辊内部进出水流道示意图

流延辊与流延膜的装配体如图4所示，长度为2500 mm，外径为740 mm，内径为573 mm，流道导程为834 mm，流道的基圆直径为650 mm，流道截面尺寸为45 mm×25 mm；流延膜厚度为0.2 mm，长度为2000 mm，包角为270°。

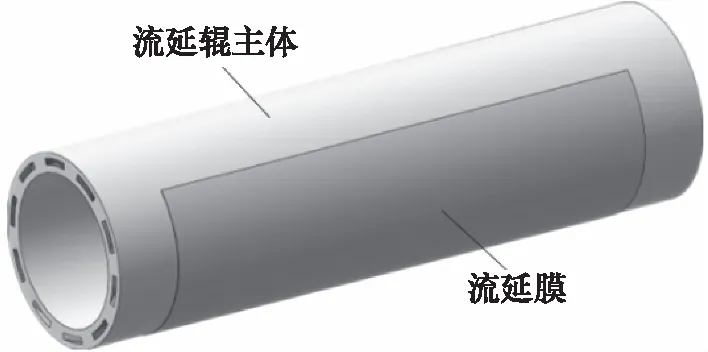
图4 流延辊与流延膜的装配体

流延辊的材质为钢，流延膜材料为聚丙烯。膜片初始温度为513 K。表1为膜片和流延辊的材料属性。

表1 材料属性

1.2 流体流动方程及传热控制方程

在生产线中，膜片流延到流延辊上冷却的过程是一个三维的非稳态传热过程。当整个冷却过程达到稳定状态时，外部环境参数也趋近于稳定，流延膜与流延辊的温度场仅在很小的范围内周期性波动，此时可以认为流延膜、流延辊和冷却水的传热过程是稳态传热。流体流动满足质量守恒、动量守恒以及能量守恒定律，Fluent的仿真过程可以视为在连续性方程、能量守恒方程、动量守恒方程这些基本守恒定律控制下的流体流动过程的数值模拟[11-12]。

连续性方程[13]：

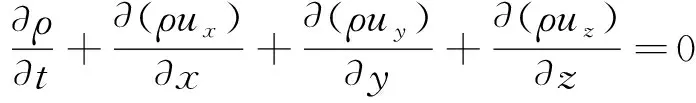
(1)

式中，ux,uy,uz分别为x,y,z三个方向的速度分量；t为时间；ρ为密度。

动量守恒方程及能量守恒方程[14]：

(2)

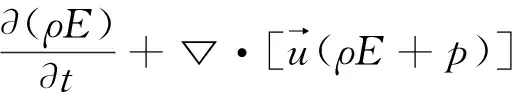
式中，p为压力；fi为微元体所受的单位质量力；τxi，τyi，τzi为偏应力在x，y，z方向上的分量；E为流体微团的总能；keff为有效导热系数；T为温度；hj为组分j的焓；Jj为扩散通量；τeff为有效偏应力；Sh为体积热源项。

选择合适的湍流模型对数值模拟结果的准确性至关重要[15]。冷却水在流延辊中以圆柱绕流的方式流动，选用Standardk-omega湍流模型，此模型对于壁面边界层、自由剪切流、低雷诺数流动有较好的适应性，对平板绕流、混合层流动、圆柱绕流等都有较好的预测。

图5 流延膜、流延辊和冷却水的网格划分

1.3 网格模型

为保证所划分的网格具有较高的质量、确保数值计算的速度和精度，划分网格时将装配体模型分割成几个规则的子块，分别对流延膜、流延辊和冷却水3个模块进行网格划分，如图5所示。膜片采用六面体网格划分，利用扫略的方法将薄膜分成6层；流延辊采用四面体和六面体混合的方式进行网格划分；冷却水的网格划分采用扫略网格的方式，并且对其添加膨胀层。网格节点数为13916634，单元数为3182737，平均扭曲度为0.209，网格质量较好。

1.4 边界条件及参数设置

辊筒中冷却水的入口采用的边界条件为速度入口，速度为1.5 m/s，温度为293 K，出口边界条件为压力出口，出口压力为标准大气压；流延辊转速为30 r/min，膜片初始温度为513 K，辊筒与空气接触表面和膜片与空气接触表面均为对流换热模型，换热系数分别为3，5 W/(m·K)，空气温度为323 K；膜片与流延辊以及冷却水与流延辊接触表面均设置为耦合传热。

在软件中，采用稳态计算方式，压力速度耦合采用coupled算法，压力插值方法选择Standard格式，湍动能和湍流耗散率的离散格式均取二阶迎风格式。

2 计算结果分析

2.1 流延膜冷却过程的温度场分析

在冷却后的流延膜出口处沿着膜片厚度方向上等间距取5条直线(分别距离膜片贴近流延辊一侧0, 0.05, 0.10, 0.15, 0.20 mm)，图6为膜片冷却过程的温度场云图及所取直线位置示意图，可以看出，随着流延辊的冷却以及空气的对流换热过程，流延膜温度逐渐降低，且温度变化幅度逐渐减小，温度逐渐趋于稳定。这是因为由于冷却水入口时温度较低，经过与流延辊的换热，冷却水在流延辊流动过程中温度不断升高，冷却水与辊筒的温差逐渐减小，换热量减小，流延膜靠近出口侧的冷却效果变差。图7为流延膜冷却后出口处的温度沿流延膜宽度方向的变化曲线，可以看出，在流延膜的宽度方向上，由于膜片两端与空气的对流换热，冷却效果显著，所以温度场呈现出较明显的中间高，两端低的现象。

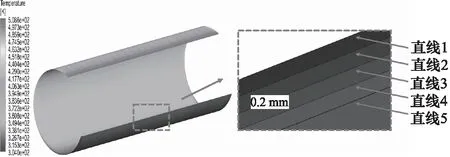
图6 流延膜冷却过程的温度场云图

2.2 单因素数值模拟

在上述5条直线上去除两端各250 mm长度的数据点(考虑切边工艺)，在每条线剩余部分上均匀地取100个点，记录这些点的温度值，计算出的均值和极差值，分别代表膜片冷却后的温度值及温度均匀性。为研究流延辊直径D对流延膜冷却效果的影响，分别在D为600，660，720，780，840 mm的条件下对膜片与流延辊装配体进行数值模拟，结果如表2所示。图8为流延膜冷却后温度均值随直径变化的曲线，图9为流延膜冷却后温度极差值随直径变化的曲线，可以看出温度均值及温度极差值都随着直径的增大呈现先增大再减小的趋势，在直径为660 mm左右温度变化较明显。这是因为由于辊筒转速一定，随着直径增大，流延辊的线速度增大，膜片与辊筒作无滑移运动，流延膜在辊筒上的线速度近似为流延辊的线速度，膜片运动速度增大，影响了冷却效果，而当辊筒直径继续增大时，膜片与辊筒的接触面积增大，散热效果变好，所以冷却效果变好。

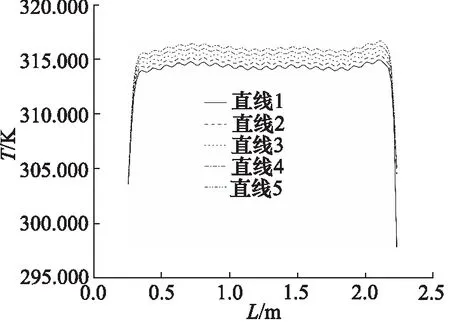
图7 流延膜冷却后温度沿流延膜宽度方向的变化曲线

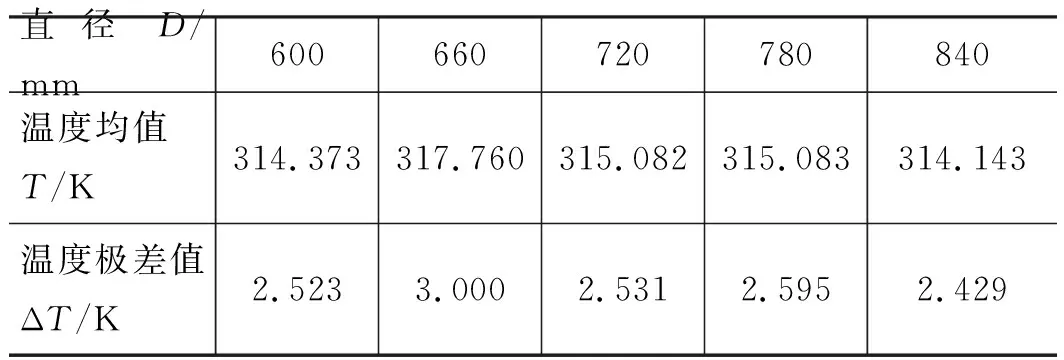
表2 不同直径下流延膜冷却后的温度

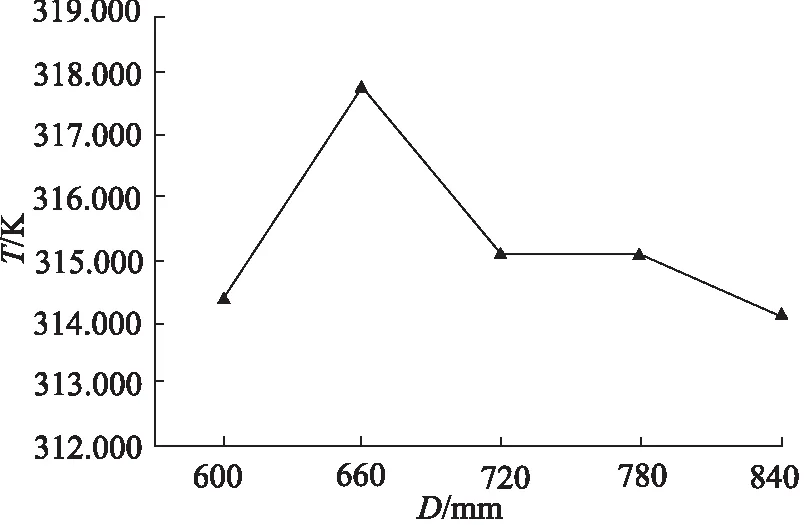
图8 流延膜冷却后温度均值随直径变化曲线

为研究流道尺寸w×h对流延膜冷却效果的影响，对膜片与流延辊装配体在不同流道宽高比下进行数值模拟。冷却水的流量及流速固定，取流道截面面积为定值，为了便于网格划分，流道的宽度w和高度h均取整数，流道法截面的宽度分别为35，40，45，50，55 mm，高度分别为32，28，25，22.5，20.5 mm，仿真结果如表4所示。图10为流延膜冷却后温度均值随流道尺寸变化的曲线，图11为流延膜冷却后温度极差值随流道尺寸变化的曲线，可以看出，流延膜冷却后的温度均值随着流道的宽高比增大而增大，变化幅度逐渐减小，而极差值随着流道的宽高比增大而减小。这是因为流道截面积一定时，随着流道宽度增大、高度减小，流道截面趋向于细长状，与流延辊表面的换热效果变差，对流延膜总体冷却效果变差，冷却效率降低，当流道宽度增大时，冷却水流道上表面接触面积变大，对流延膜厚度方向的冷却效果变好，因此冷却后的温度均匀性变好。

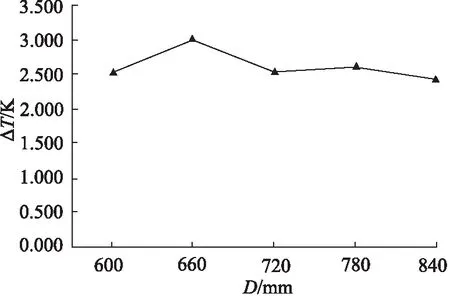
图9 流延膜冷却后温度极差值随直径变化曲线

表3 不同流道尺寸下流延膜冷却后的温度

图10 流延膜冷却后温度均值随流道尺寸变化曲线

图11 流延膜冷却后温度极差值随流道尺寸变化曲线

为研究流道导程s对流延膜冷却效果的影响，分别在s为634，734，834，934，1034 mm的条件下对膜片和流延辊的装配体进行数值模拟，结果如表3所示。图12为流延膜冷却后温度均值随导程变化的曲线，图13为流延膜冷却后温度极差值随导程变化的曲线，可以看出，膜片冷却后的温度均值和极差值均随着导程的增大而增大，变化幅度逐渐减小。这是因为当导程增大时，流延辊内部的流道密度减小，辊筒与冷却水的接触面积减小，辊筒表面的温度升高，对膜片的冷却效果变差。

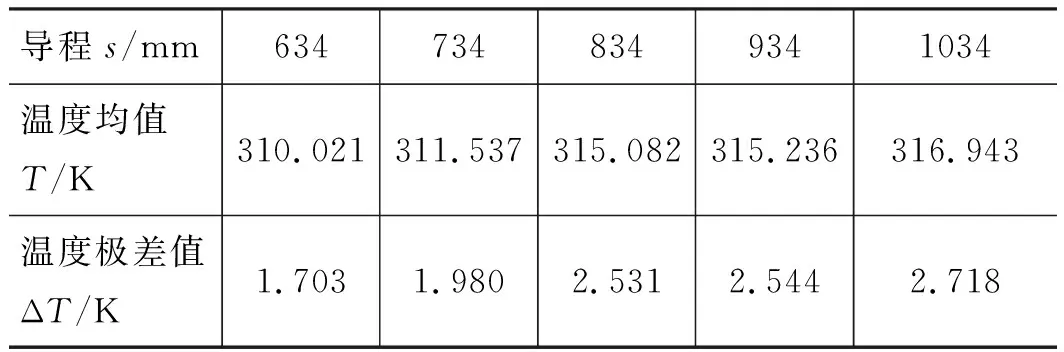
表4 不同导程下流延膜的温度

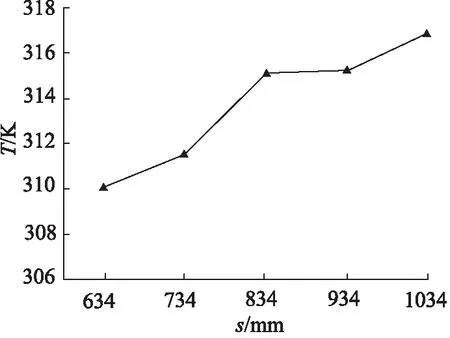
图12 流延膜冷却后温度均值随导程变化曲线

2.3 多因素正交设计仿真分析

利用Design-Expert 8.0软件，针对单因素优选结果，对辊直径D、流道尺寸w×h、导程s3个参数进行优化。选取流延膜冷却后出口处的平均温度及温差值作为优化目标，建立正交试验表对流延膜冷却效果进行数值模拟，因素水平表如表5所示。仿真试验结果如表6所示。

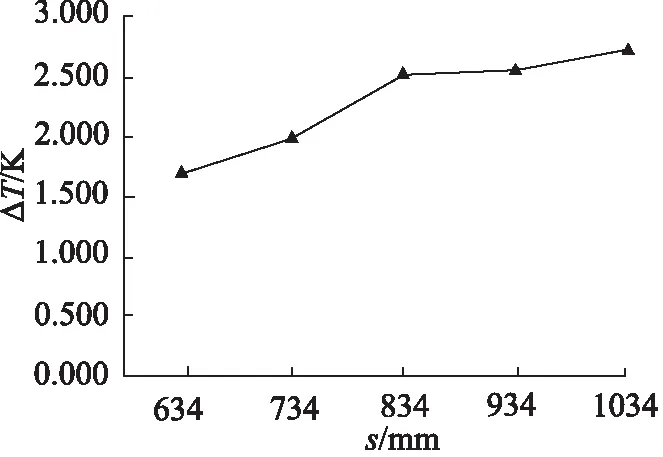
图13 流延膜冷却后温度极差值随导程变化曲线

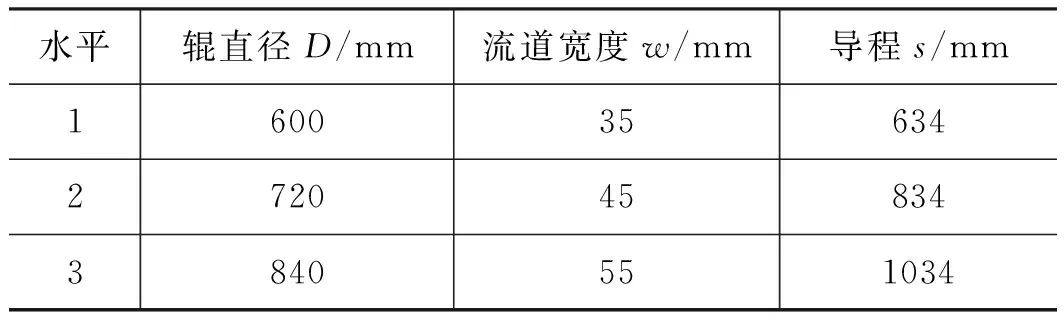
表5 因素与水平

表6 正交设计仿真结果

根据数据样本，得到温度均值和温度极差值的二次多项回归模型：

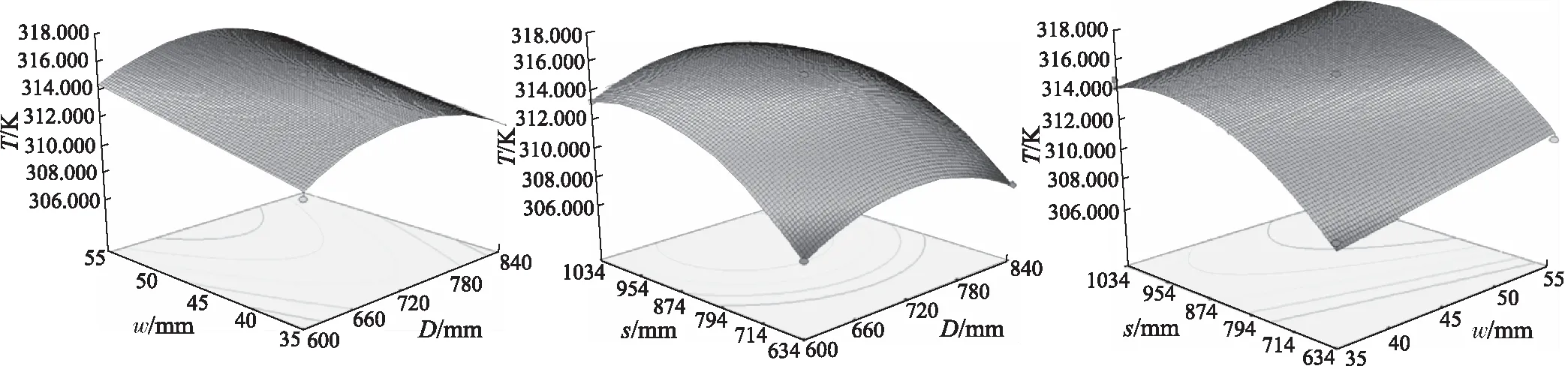
图14 温度均值的交互响应面

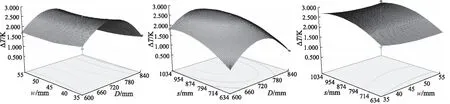
图15 温度极差值的交互响应面

T=315.08+0.016D+1.48s+2.95w-0.12Ds-0.14Dw-0.082sw-2.36D2+0.11s2-2.52w2

(4)

ΔT=2.53-0.19D-0.072s+0.38w-0.0005Ds-0.15Dw+0.033sw-1.01D2+0.13s2-0.38w2

(5)

式中，T为流延膜冷却后出口处的温度均值；ΔT为流延膜冷却后出口处的温度极差值；D为辊直径；w为流道宽度；s为流道导程。两模型的决定系数R2与校正决定系数分别为0.9862，0.9813，均接近于1，变异系数与精密度分别为：0.17%和6.93%、24.408和19.176，说明两个拟合回归模型具有较高的可靠性。

考虑到流延膜的结晶问题，针对回归模型，运用Design-Export 8.0软件中的Optimization功能，以流延膜温度均值范围为315～320 K、温度极差值最小为条件，求解回归模型得到流延辊最优结构参数为直径838.01 mm、流道尺寸55 mm×20.5 mm、导程961.39 mm。此时优化后的温度均值为315 K，温度极差值为0.892 K，优化后的温度均值和温度极差值较最初值分别降低了0.082 K，1.639 K。

2.4 交互响应面分析

根据回归模型结果，利用Design-Expert 8.0进行各个因素交互响应面的绘制。辊直径与流道尺寸、辊直径与流道导程以及流道尺寸与流道导程分别对膜片温度均值的交互响应面，如图14所示，当辊筒直径增大时，温度均值呈先增大后减小的趋势；当流道宽高比增大时，温度均值也增大；流道的导程及宽高比越大，温度均值越大。辊直径与流道尺寸、辊直径与流道导程以及流道尺寸与流道导程分别对膜片温度极差值的交互响应面如图15所示，当辊筒直径增大时，温度极差值呈先增大后减小的趋势；当流道宽高比增大时，温度极差值减小；流道的导程越大，温度极差值越大。

3 结论

(1) 通过数值模拟仿真分析可知，随着流延辊的冷却以及空气的对流换热过程，流延膜温度逐渐降低，温度降低幅度逐渐减小，在流延膜的宽度方向上，温度场呈现出中间高两端低的现象；

(2) 通过单因素仿真试验可知，流延膜的冷却效率及冷却后的温度均匀性都随着辊直径的增大呈现先降低再升高的趋势，除此之外，流延膜的冷却效率随着流道宽高比及流道导程的增大而降低，流延膜冷却后的温度均匀性随着流道宽高比增大而提升，随着流道导程的增大而降低；

(3) 通过对辊直径、流道尺寸、流道导程的正交设计仿真，以流延膜冷却后出口处的温度均值及温度极差值作为优化参数指标，建立回归模型，求解得到最优参数组合为直径838.01 mm、流道尺寸55 mm×20.5 mm、导程961.39 mm，此时优化后的温度均值为315 K，温度极差值为0.892 K，优化后的温度均值较最初值降低了0.082 K，温度极差值降低了1.639 K。