基于流体模型的碳纳米管电离式传感器的结构优化方法*

吴健 韩文 程珍珍 杨彬 孙利利 王迪朱程鹏 张勇† 耿明昕 景龑

1) (西安交通大学电气工程学院, 电力设备电气绝缘国家重点实验室, 西安 710049)

2) (国网陕西省电力公司电力科学研究院, 西安 710199)

与常规电离式传感器相比, 碳纳米管三电极电离式气体传感器具有体积小、工作电压低的优势, 对智能电网、泛在物联网的发展具有重要作用, 但存在输出电流低、灵敏度低的缺点, 需要从结构上对其进行优化.本文基于汤生放电原理, 采用COMSOL Multiphysics 多物理场直接耦合分析软件, 建立了传感器二维等离子体放电流体仿真模型.研究得到了8 种不同结构的传感器, 在氮气背景中的静电场分布及传感器收集极平均电流密度.通过对比不同结构参数下的电场强度及电流密度值, 得到了最优传感器结构.结合仿真结果, 制备了8 种优化结构的传感器进行实验验证, 最优传感器结构具有最高的收集电流密度, 与仿真结果一致, 证明了本文提出的结构优化方法的可行性.基于最优结构, 制作了100 和120 µm 极间距的传感器, 获得了NO/SO2两组分混合气体的敏感特性.与其他技术相比, 最优传感器的灵敏度比现有技术高1—2 个数量级, 展示了三电极电离式碳纳米管传感器的应用潜力.

1 引 言

随着工业、农业等基础行业以及电子、IT 等新兴行业的共同发展, 国家对电力、煤炭等能源物联网的发展提出了更高的要求, 而气体传感器能够为物联网实时地, 按一定频率周期地采集环境信息,是物联网至关重要的组成部分[1,2].目前, 金属氧化物半导体(MOS)传感器[3,4]和固态电解质传感器[5,6]占据着气体传感器的绝大部分市场.但二者都需要在较高温度下工作, 消耗功率大、灵敏度低、抗干扰能力较差, 使用不便.碳纳米管(CNTs)具有优良的物理化学特性及气敏特性, 成为了一种新型气体敏感材料, 基于CNTs 的气体传感器展现出了比前两者更快的反应速度, 更大的灵敏度, 而且能在室温下工作.其中吸附式碳纳米管气体传感器[7,8]普遍具有易饱和、测量范围窄、解吸附时间长, 且需要经过复杂的修饰改性工艺等缺点, 使其应用受到了极大的限制.而碳纳米管电离式传感器基于气体放电原理, 利用其纳米尖端能够在低电压下产生较高的电场强度, 使气体发生电离; 电离形成的离子被传感器极板收集, 通过收集电流的大小获得被测量的值[9−12]; 能够检测多种气体, 具有功耗低、抗干扰能力强等优势; 但仍然存在收集电流小、灵敏度低的缺点.传感器的结构影响着放电场域空间的电场分布, 进而影响气体电离及正离子的产生, 最终影响传感器的性能; 因此, 需要对传感器的结构进行优化, 提高传感器的输出电流, 增加传感器灵敏度, 提高传感器的性能.

由于等离子体被看成是一种多成份 (电子、离子和中性粒子) 的流体, 通过求解各种粒子相应的流体力学方程组, 并耦合质量守恒方程、电子能量守恒方程及泊松方程, 得到等离子体的一些宏观和微观特性.因此近年来, 许多国内外学者和专家提出了基于流体模型的静电场和低温等离子体仿真方法, 用于传感器结构和电极间粒子的运动分析.Govardhan 等[13]基于COMSOL 有限元仿真对金属氧化物半导体气体传感器的结构优化进行了建模, 完成了传感器气体敏感室的结构优化.Wilde和Lai[14]采用COMSOL 软件建立了涡流传感器监测系统模型, 优化了涡流传感器的结构参数.Atieh[15]基于流体模型, 针对两电极击穿型电离式碳纳米管气体传感器做了结构优化, 通过减小电极间距和生长直立碳纳米管, 降低了击穿电压.Chivu等[16]基于COMSOL 软件, 对两电极击穿型电离式纳米线气体传感器做了结构优化, 主要分析纳米线结构形貌对击穿电压的影响.以上研究均证明了采用流体模型及COMSOL 仿真软件进行传感器结构优化的可行性.因此, 本文也选用COMSOL Multiphysics 多物理场直接耦合分析软件, 对传感器的静电场及极间放电进行仿真建模, 通过分析不同结构下的静电场分布、场域空间放电过程 (离子密度、电子密度等) 及收集电流的大小, 来获得引出电流大、灵敏度高的传感器优化结构, 为确定及制作何种结构的电离式传感器提供了科学依据.

2 传感器的工作原理及仿真模型的建立

2.1 传感器的工作原理

传感器结构示意图如图1 所示 (1#传感器),传感器由3 个电极构成, 分别为碳纳米管阴极、引出极和收集极.3 个电极尺寸相同, 阴极具有两个圆形扩散孔, 引出极中心具有1 个圆形引出孔, 收集极中心有1 个长方形盲孔.3 个电极之间由绝缘层隔离, 不同厚度的绝缘层可用来调节传感器的极间距, 传感器的阴极-引出极间距d与引出极-收集极间距d相同.

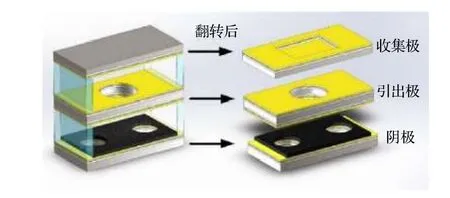
图1 碳纳米管三电极传感器示意图Fig.1.Schematic diagram of the carbon nanotube triple electrode sensor.

三电极传感器测量电路如图2 所示, 工作时阴极接地、引出极-阴极间加直流电压Ue、阴极-收集极加直流电压Uc,Ue>Uc.通过电极电压控制方式在传感器的极间产生两个反向电场E1和E2.由于碳管具有纳米尖端形貌, 因此在碳纳米管尖端附近有较高的电场强度, 气体分子通过碰撞电离产生电子和正离子, 大多数的正离子会向引出极扩散.通过引出孔后, 在反向电场E2的作用下, 正离子会加速运动到收集极, 作为传感器的输出电流Ic输出.

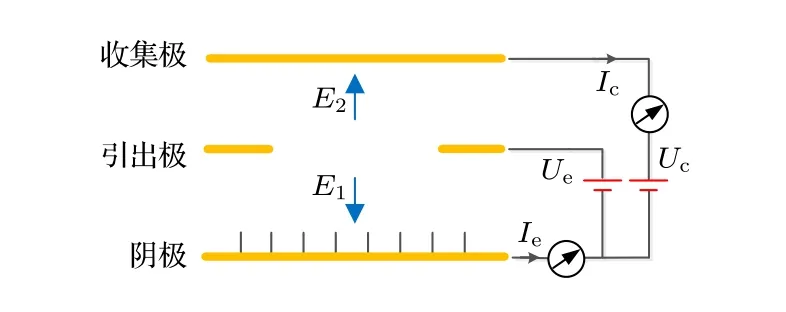
图2 传感器测量电路示意图Fig.2.Schematic diagram of the measuring circuit.

三电极传感器工作在非自持放电状态, 基于气体放电理论, 气体第一电离系数α和场强E及压力P存在指数关系[17], 即

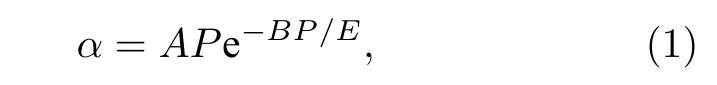
式中,A和B是与气体成分、温度有关的常数;P为气体分压强, 取决于气体浓度φ;E为电场强度.

同时, 收集电流Ic为总放电电流I的一部分[17],

式中,I0为初始放电电流.因此, 当传感器结构固定时, 收集电流Ic的值取决于传感器极间距d、气体浓度φ与温度T.

传感器内部电场分布将根据传感器结构的变化而发生改变, 正向电场E1的分布变化会影响电子发射及电子能量的分布, 进而影响到正离子的生成; 反向电场E2的分布变化会影响收集极对正离子的收集, 最终影响收集电流Ic的大小.因此,对传感器结构的优化能够提升传感器收集电流的大小, 提高传感器的检测性能.

2.2 传感器静电场仿真模型的建立

选择COMSOL 软件中的静电模块建立传感器静电场仿真模型.由于电极结构和电极电压是电场分布的决定因素, 所以建立三电极电离式碳纳米管传感器极间电场的二维仿真模型时, 需要在简化模型时尽可能多包含传感器电极的几何结构特点,便于求解计算.沿图3(a)左一图虚线所示截面, 依次截取获得图3(a)右二、右一图所示截面, 用来建立传感器的二维轴对称模型, 并在阴极上均匀设置碳纳米管阵列(图3(b)).图3 的建模参数如表1所列 (该结构为1#传感器).

1) 仿真模型静电特性的控制方程及边界条件

对于静电场模型, 采用拉普拉斯方程描述空间场域电场分布, 控制方程如下:

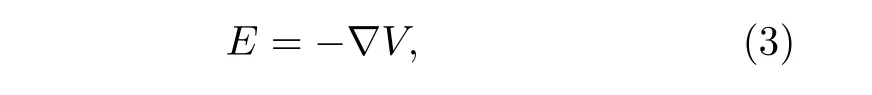
式中,E为电场强度,V为电势.

模型边界条件如下:

式中,V0为电极边界的电势.

根据传感器电路测量示意图可知: 对于阴极边界,V0= 0 V; 对于引出极边界,V0= 100 V; 对于收集极边界,V0= 1 V.模型添加的边界条件如图4 所示 (图中长度单位是µm).

2) 网格剖分

模型采用自由三角剖分, 网格剖分尺寸设置如表2 所列.

剖分后获得传感器模型的网格剖分如图5 所示, 图中长度单位是µm.

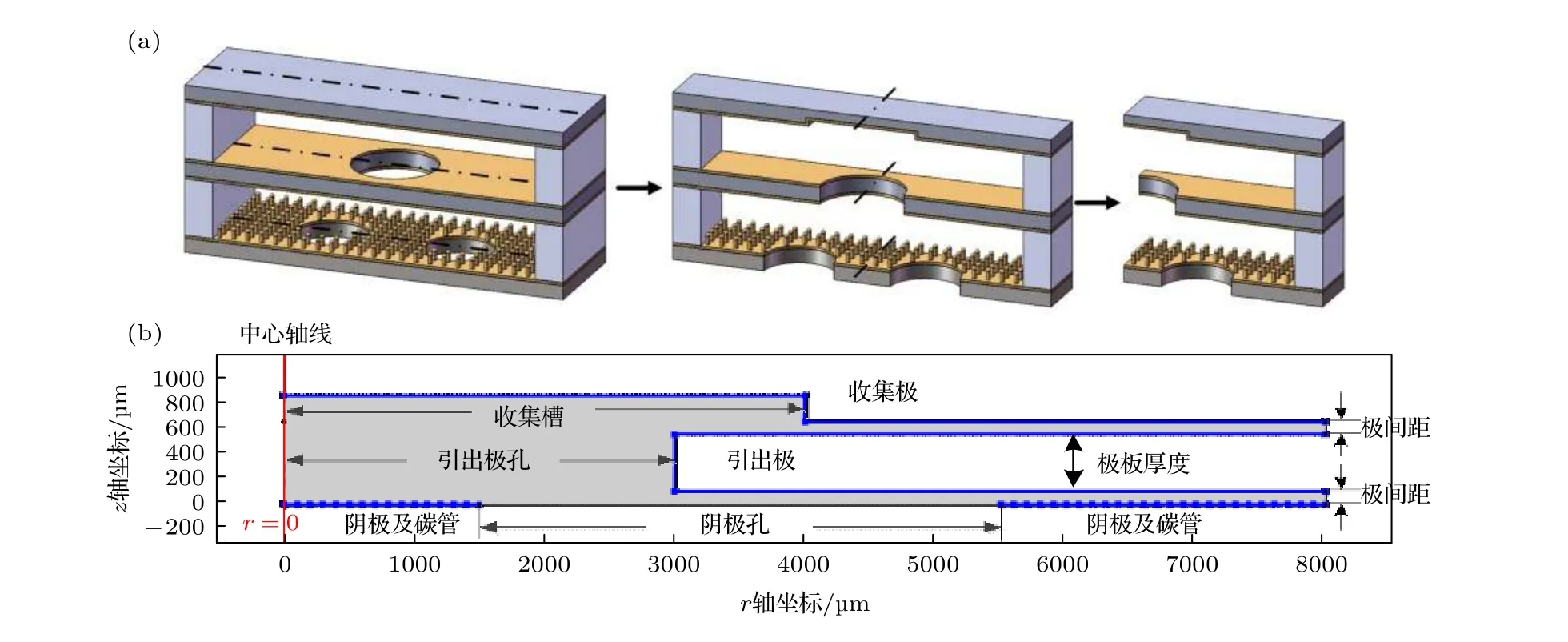
图3 传感器仿真模型 (a) 传感器的二维模型示意图; (b) 传感器的静电场二维轴对称仿真场域模型Fig.3.Simulation model: (a) Longitudinal section diagram of the two-dimensional model; (b) two-dimensional axisymmetric field simulation model of the electrostatic field.

表1 仿真建模参数Table 1.Parameters of the simulation model.

表2 网格剖分尺寸Table 2.Mesh size of the model.

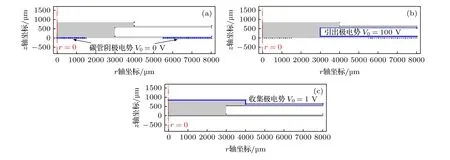
图4 模型添加的边界条件 (a) 阴极边界; (b) 引出极边界; (c) 收集极边界Fig.4.Boundary conditions: (a) The cathode; (b) extracting electrode; (c) collecting electrode.

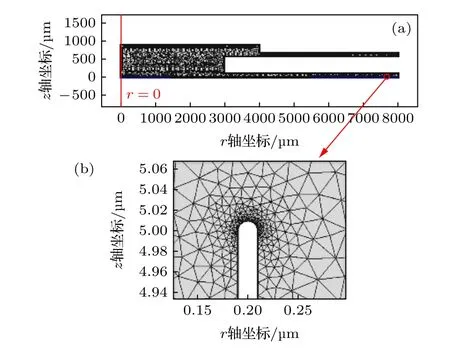
图5 传感器极间一半场域模型网格剖分图 (a) 极间一半场域剖分; (b) 单根碳管周边局部场域剖分Fig.5.Grid mesh of sensor model in the half region of interelectrode: (a) Mesh in the half region of interelectrode;(b) mesh in the local region around carbon nanotube.

3) 求解以及结果处理

选择COMSOL 的稳态求解器, 采用有限元方法对静电场模型进行直接迭代计算, 即可获得仿真结果.通过对仿真结果中正向电场与反向电场分布分析, 为电极结构的优化提供科学依据.

2.3 传感器极间放电仿真模型的建立

采用2.2 节静电场建模中介绍的二维轴对称模型, 基于以下流程建立传感器极间放电模型.

1) 气体基本粒子及其化学反应的添加

碳纳米管电离式传感器的检测背景是氮气, 主要的活性粒子包括电子、正离子()、激发态粒子和基态粒子(N2)等.化学反应包括气体放电空间中的化学反应和电极与材料表面的化学反应.主要反应方程如表3 所列[18−21], 包括电子碰撞反应 (R1—R7) 和重粒子反应 (R8—R15).

在传感器电极表面, 各种粒子都会跟电极作用, 发生表面化学反应, 反应生成物有的在电极上消失, 有的回馈到等离子体中, 还需要在模型中添加表面化学反应, 参数如表4 所列.其中γe为二次电子发射系数,εr为二次电子平均能量.

2) 场域模型的控制方程

流体模型通过求解质量守恒方程、能量守恒方程和泊松方程来求解等离子体内部各种粒子密度[22].

3) 场域模型的边界条件

(1) 粒子质量守恒方程边界条件

电子、离子会在电场和热运动下轰击传感器电极, 被电极完全吸收, 同时正离子轰击电极还可能发生二次电子发射.对于电子, 边界通量是电场迁移形成的通量、热运动形成的通量和正离子轰击阴极发射二次电子形成的通量之和, 如(5)式; 而对于正离子和负离子的边界条件分别如(6)式和(7)式所示:

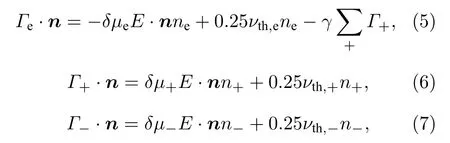
式中,Γe为电子通量;Γ+为正离子通量;Γ–为负离子通量;n为电极边界外法线向量;µe为电子迁移系数;µ+为正离子迁移系数;µ–为负离子迁移系数;ne为电子密度;n+为正离子密度;n–为负离子密度;νth为粒子热运动速度;γe为离子轰击阴极的二次电子发射系数; 下角标“+”代表正离子, 下角标“–”代表负离子; 当带电粒子运动方向跟电极边界外法向向量一致时,δ取值1, 否则为零.

表3 气体电离流体仿真模型的区域反应Table 3.Regional reactions of the fluid simulation model on gas ionization.

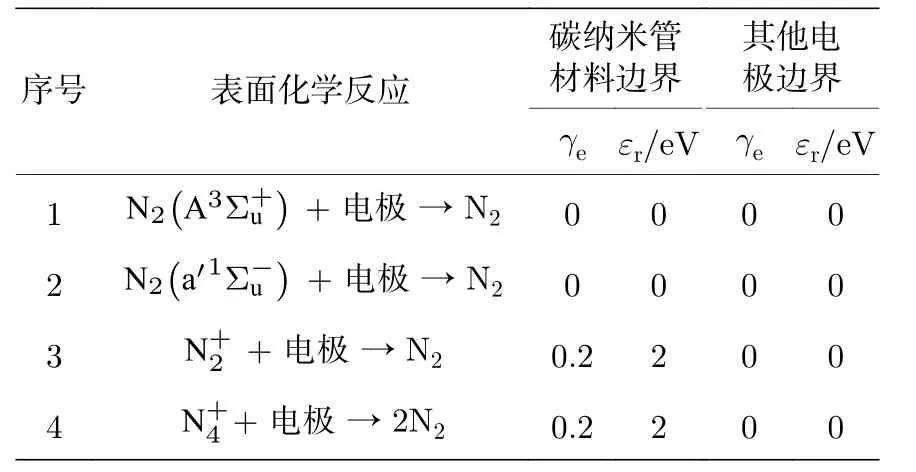
表4 电极表面化学反应Table 4.Chemical reactions on the electrode surface.

对于中性粒子, 电极边界条件主要取决于中性粒子的热运动.因此, 中性粒子的电极边界条件为

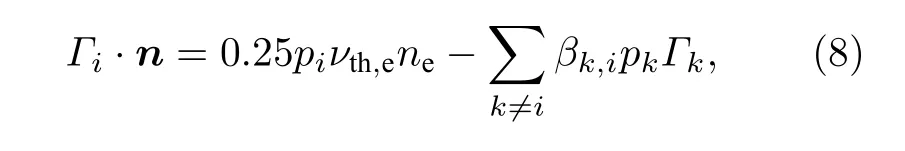
式中,p为中性粒子与电极表面的反应率; 若第k种粒子与电极表面反应转换为第i种粒子,βk,i为1, 否则为零.

(2) 电子能量守恒方程边界条件

电子能量在边界的通量由热运动电子能量的通量和二次发射电子的能量通量之差构成, 所以电子温度守恒方程的边界条件为

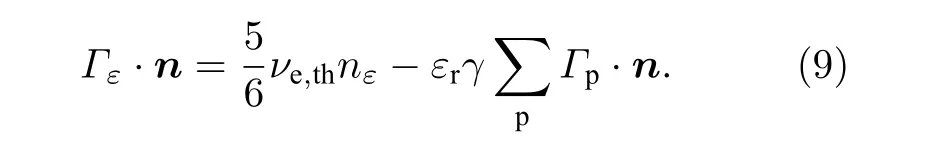
式中,Γε为电子平均能量通量,νe,th为电子热运动速度;εr为二次发射电子的能量;Γp为二次发射电子能量通量.

(3) 泊松方程边界条件

阴极一端接地, 引出极一端接100 V 电压, 收集极接1 V 电压.

4) 传感器放电模型的求解

模型依旧采用自由三角剖分, 剖分参数与2.2 节相同.由于有限体积法具有很好的守恒性,可以克服泰勒展开离散的缺点, 对网格的适应性也很好, 因此采用有限体积法进行数值求解.计算时通过逐步调节空间网格和时间步长来实现结果收敛, 当相对误差小于0.001 时, 结束本次迭代, 进行下一步迭代计算.设置的时间步长: 从10–11s 开始,以100.06s 为步长, 计算到0.1 s 结束.

求解过程中, 根据表3 和表4 中的反应式, 耦合(5)—(9)式, 可以计算获得电子浓度ne、正离子浓度n+等参量, 在结果中查看这些参量并了解其分布情况, 进而可以计算得到电流密度jc:

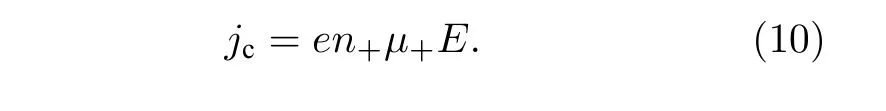
3 传感器的结构优化仿真

采用2.2 节静电场仿真模型, 获得了1#传感器的电场分布 (图6), 蓝色区域正向电场小于零,红色区域反向电场大于零, 蓝色和红色区域交界是电场为零的边界.1#传感器在引出孔中间较大范围内没有反向电场, 致使部分正离子不能通过迁移到达收集极, 减小了正离子收集量, 从而影响传感器收集电流的大小, 影响传感器的灵敏度.增加收集电流及灵敏度, 成为传感器结构优化研究的方向.本文分别从传感器的3 个电极出发, 建立不同结构传感器放电流体模型, 在相同条件下仿真获得不同结构传感器的收集电流, 确定最优化传感器结构.

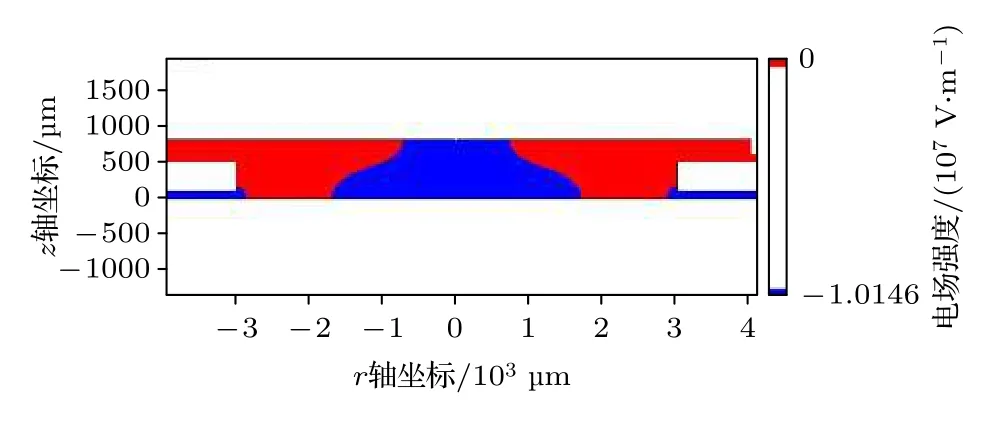
图6 传感器的纵向电场分布Fig.6.Longitudinal electric field distribution of the sensor.

3.1 收集极结构对传感器放电过程的影响

收集极用于收集正离子, 形成传感器的输出电流Ic.设计研究4 种不同形貌的收集极电极结构, 保持引出极和阴极结构不变, 即引出极中心有一个直径为6 mm 的引出孔, 阴极有两个直径为4 mm 的透气孔, 如图7 所示.图7(a) 1#传感器收集极中心有一个尺寸为6 mm × 8 mm 深度为200 µm 的矩形盲孔 (考虑硅片面积只有14 mm ×10 mm, 而且硅片两边还需要粘接绝缘条和导线,所以, 收集极盲孔面积取6 mm × 8 mm).图7(b)2#传感器是平板收集极, 用于研究中心矩形盲孔是否对传感器收集电流有作用.图7(c) 3#传感器是在图7(a)基础上, 将收集极中心矩形盲孔深度200 µm 减小为50 µm, 用于矩形盲孔深度对传感器性能的研究.图7(d) 4#传感器是将图7(a)中的一个中心矩形盲孔设计为12 个1.2 mm × 1.2 mm深度为200 µm 的小矩形盲孔, 研究这种分散矩形盲孔对传感器收集正离子是否有帮助.

建立这4 种结构传感器的放电流体模型, 其中, 传感器极间距均为100 µm, 放电环境为氮气,气压为1 个标准大气压, 温度为30 ℃, 在Ue=100 V 和Uc= 1 V 条件下, 仿真获得4 种不同结构的传感器放电参数, 如表5 所列.

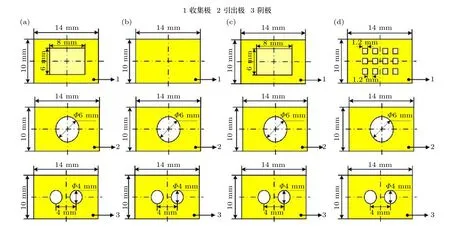
图7 4 种不同收集极结构的传感器电极示意图 (a) 1#传感器; (b) 2#传感器; (c) 3#传感器; (d) 4#传感器Fig.7.Schematic diagram of the electrodes with four different collecting structures: (a) 1# sensor; (b) 2# sensor; (c) 3# sensor;(d) 4# sensor.

由表5 可知, 对比1#和2#传感器, 当传感器收集极有盲孔时, 仿真电子浓度、正离子浓度、平均收集电流密度, 比没有盲孔的收集极更大, 这说明盲孔有助于传感器收集更多正离子.对比1#和3#传感器, 当盲孔深度由200 µm 减小为50 µm时, 传感器放电参数均有所减小, 放电强度减弱,这说明盲孔深度越深, 产生和收集的正离子越多.考虑硅片厚度只有450 µm, 因此, 收集极盲孔深度取200 µm.1#和4#传感器相比, 中心有一个尺寸为6 mm × 8 mm、深度为200 µm 的矩形盲孔的电极, 相比4#传感器收集极的多个小矩形盲孔,具有较大的平均收集电流密度.因此, 收集极中心有一个尺寸为6 mm × 8 mm, 深度为200 µm 矩形盲孔的1#传感器结构, 是4 种收集极结构中的最优结构(图7(a)).

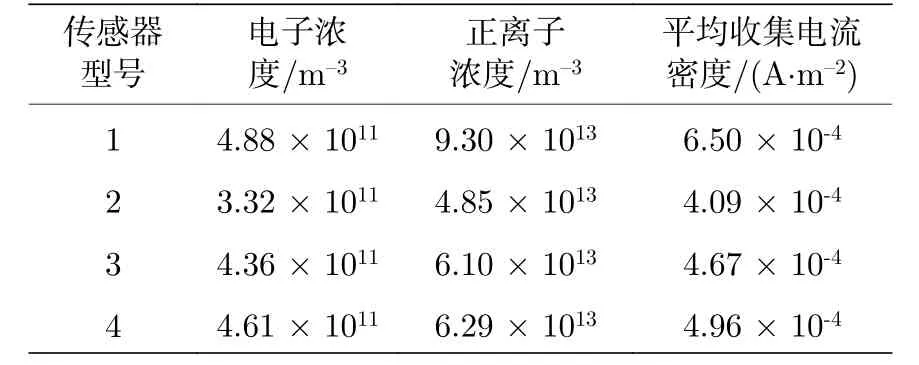
表5 4 种不同收集极结构的传感器的仿真放电参数Table 5.Simulation discharge parameters of the four sensors with different collecting electrode structures.

3.2 引出极结构对传感器放电过程的影响

在3.1 节中获得的1#传感器收集极为优化结构的基础上, 保持收集极和阴极结构不变, 即收集极中心有1 个尺寸为6 mm × 8 mm、深度为200 µm 的矩形盲孔, 阴极有两个直径为4 mm 的透气孔, 建立引出极引出孔直径分别为4, 3, 2, 1.2和1 mm 的传感器静电场仿真模型 (图8), 研究不同引出极结构的影响.

由图6 和图8 可知, 随着引出孔的孔径由6 mm逐渐减小到1 mm, 反向电场红色场域先增大后减小, 当引出孔孔径为1.2 mm 时, 反向电场场域面积最大.根据传感器不同孔径引出极静电场仿真结果, 建立了3 种结构传感器(图9)的放电流体模型.图9(a) 1#传感器引出极有1 个直径为6 mm的引出孔, 图9(b) 5#传感器引出极有6 个直径为2 mm 的引出孔, 图9(c) 6#传感器引出极有9 个直径为1.2 mm 的引出孔.仿真获得了3 种不同引出极结构的传感器仿真放电参数, 如表6 所列.

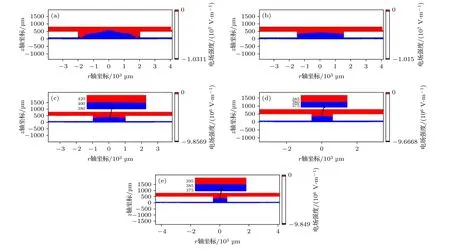
图8 不同引出孔直径传感器静电场仿真 (a) 引出孔直径4 mm; (b) 引出孔直径3 mm; (c) 引出孔直径2 mm; (d) 引出孔直径1.2 mm; (e) 引出孔直径1 mmFig.8.Electrostatic field simulation of the sensors with different outlet diameters of (a) 4 mm, (b) 3 mm, (c) 2 mm, (d) 1.2 mm,and (e) 1 mm.

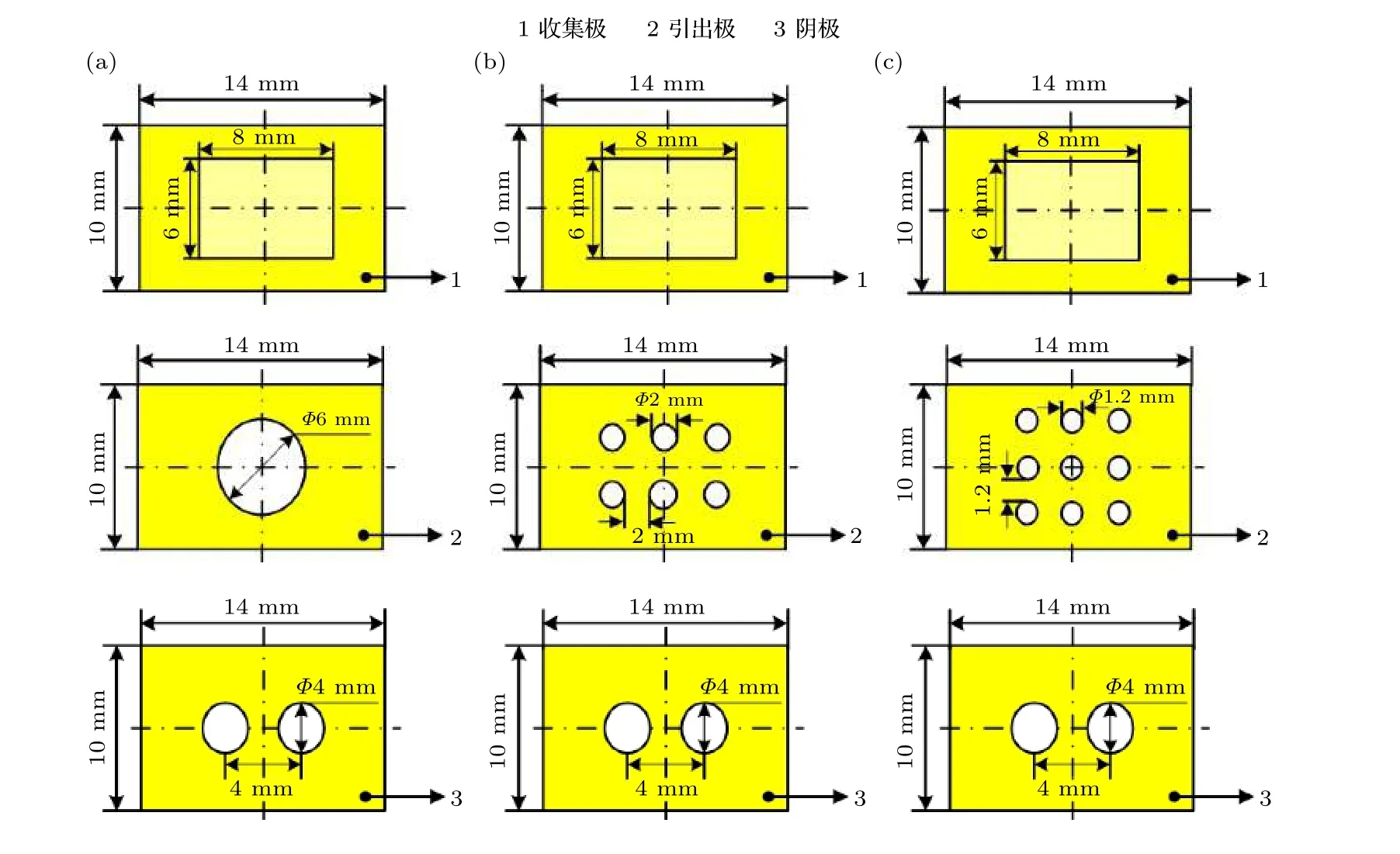
图9 3 种不同引出极结构的传感器电极示意图 (a) 1#传感器; (b) 5#传感器; (c) 6#传感器Fig.9.Schematic diagram of the electrodes with three different extracting electrode structures: (a) 1# sensor; (b) 5# sensor; (c) 6#sensor.

表6 3 种不同引出极结构的传感器的仿真放电参数Table 6.Simulation discharge parameters of the three sensors with different extracting electrode structures.

1#, 5#和6#传感器的放电参数仿真对比(表6)说明, 引出极具有9 个直径为1.2 mm 引出孔的6#传感器放电参数仿真结果最大.因此,6#传感器所具有的9 个直径为1.2 mm 的引出孔结构, 是最佳引出极结构.

3.3 阴极结构对传感器放电过程的影响

原有传感器阴极有两个直径为4 mm 的扩散孔, 有利于气体的扩散及热量的散失.保持收集极和引出极结构不变, 即收集极中心有一个尺寸为6 mm × 8 mm 深度为200 µm 的矩形盲孔 (基于1#传感器优化结果), 引出极有9 个直径为1.2 mm的引出孔 (基于6#传感器优化结果), 分别设计研究3 种不同孔径的阴极电极结构, 如图10 所示.其中, 图10(a) 6#传感器阴极结构设计了两个直径为4 mm 的扩散孔, 图10(b) 7#传感器阴极结构设计了两个直径为3 mm 的扩散孔, 图10(c) 8#传感器阴极结构设计了两个直径为2 mm 的扩散孔.建立了这3 种结构传感器的放电流体模型, 仿真获得了3 种不同阴极结构的传感器放电参数(表7).

由表7 可知, 6#和7#传感器相比, 当传感器阴极孔径由4 mm 减小到3 mm 时, 仿真放电参数均变大.但是, 当8#传感器阴极孔径减为2 mm时, 传感器放电参数反而减小, 说明阴极孔径太小,不利于传感器收集更多正离子.因此, 6#, 7#和8#传感器的对比说明, 7#传感器所具有的有2 个直径为3 mm 通孔的阴极, 是最佳阴极结构.

通过传感器收集极、引出极和阴极结构的优化, 仿真获得7#传感器为最优电极结构, 即收集极中心有1 个尺寸为6 mm × 8 mm、深度为200 µm的矩形盲孔, 引出极有9 个直径为1.2 mm 的引出孔, 阴极有2 个直径为3 mm 的阴极孔.

3.4 传感器结构优化的实验验证

为了验证传感器结构优化仿真结果的正确性以及仿真优化方法的可行性, 按照图7、图9 和图10所示的1#—8#传感器结构, 分别制作了极间距均为100 µm 的1#—8#八只传感器.

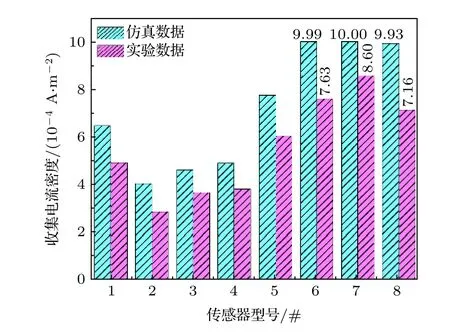
图11 仿真与实验电流密度对比Fig.11.Comparison of current densities obtained through simulation and experiment.

在与仿真相同条件下, 实验测量了8 个不同结构传感器的收集电流Ic.已知传感器收集极极板面积Se为140 mm2(14 mm × 10 mm), 实验收集电流密度jc等于收集电流Ic除以收集极极板面积Se,由此计算出实验收集电流密度, 与仿真平均收集电流密度进行对比(图11).虽然仿真和实验所获得的收集电流密度有些差异, 但气体放电流体模型仿真的收集电流密度变化趋势与实验结果相近, 说明建立的气体电离流体模型可以在一定程度上反映传感器结构变化的真实情况, 因此采用仿真方法来优化传感器结构不仅是可行的, 而且可以降低传感器的设计成本.图11 说明, 7#传感器具有最大的收集电流密度, 为最优结构, 与仿真结果一致.

4 优化结构的传感器对NO/SO2 两组分混合气体的响应特性

采用两只极间距分别为100 µm 和120 µm 的优化结构传感器, 检测了两组分混合气体NO/SO2,实验条件如表8 所列.其中, 100 µm 传感器用来检测NO 浓度, 120 µm 传感器用来检测SO2浓度.实验获得了传感器阵列收集电流与氮气背景中NO 和SO2两组分混合气体浓度的响应特性曲线(图12).由图12 看出, 阵列中两个传感器的响应特性曲线, 都随NO 和SO2气体浓度的增大而呈现单调下降趋势, 而且不同极间距传感器的响应特性显著不同.对于100 µm 极间距的NO 传感器, SO2浓度不变时, 收集电流随着NO 体积分数从0 增加到1114 × 10–6而单调递减; 并在不同的SO2浓度下, 获得了四条截然不同的响应特性曲线(图12(a)).对于120 µm 极间距的SO2传感器,NO 浓度不变时, 收集电流随着SO2体积分数从0 增加到735 × 10–6而单调递减; 并且在不同的NO 浓度下, 获得了四条截然不同的响应特性曲线(图12(b)).表明传感器既可以检测单一气体浓度,也可以同时检测混合气体, 能够很好地识别混合气体组分.

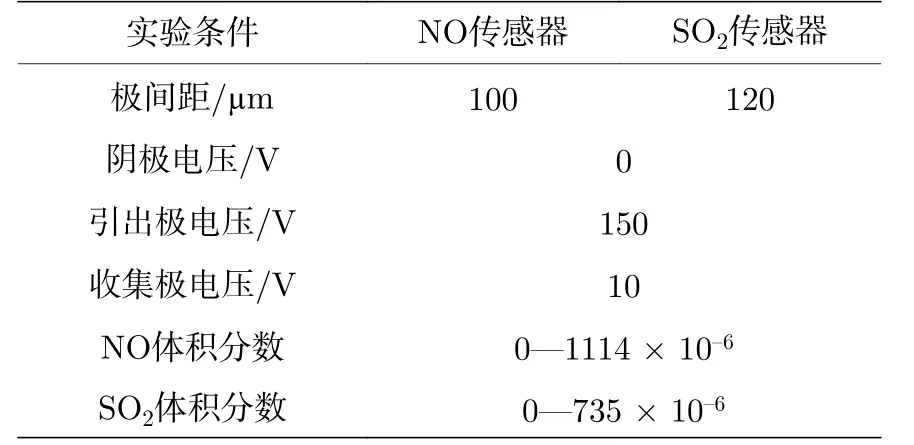
表8 传感器阵列测量NO 和SO2 两组分混合气体的实验条件Table 8.Experimental conditions of NO and SO2 mixtures detection with a sensor array.

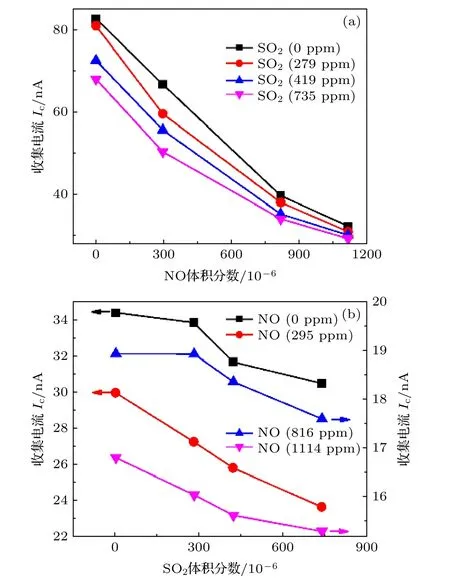
图12 氮气背景NO 和SO2 混合气体敏感特性曲线 (a) 不同SO2 的体积分数(1 ppm = 10–6)下100 µm 极间距NO传感器收集电流与NO 的体积分数的关系曲线; (b) 不同NO的体积分数下120 µm 极间距SO2 传感器收集电流与SO2的体积分数的关系曲线Fig.12.Sensitivity characteristic curves of the sensor array for measuring NO and SO2 mixture in nitrogen: (a) Collecting currents of the NO sensor with the electrode spacing of 100 µm versus volume fraction of NO under different volume fractions of SO2; (b) collecting currents of the SO2 sensor with the electrode spacing of 120 µm versus volume fraction of SO2 under different volume fractions of NO.

灵敏度数值是衡量传感器性能的一个重要指标, 灵敏度越高, 表示相同的输入改变量引起的输出变化量越大, 性能越好.为了与其他不同原理的传感器对比, 灵敏度计算时输出量采用相对变化量形式:

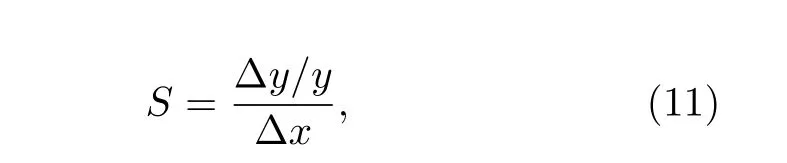
式中, Δx和Δy分别为输入量和输出量的变化量,y为输出量程.碳纳米管三电极传感器与现有NO和SO2传感器产品的性能相比(表9)[23−27], 碳纳米管三电极传感器的灵敏度高了1—2 个数量级,说明经过本文优化方法对传感器结构的优化, 使得三电极电离式碳纳米管结构传感器的性能得到了提升, 不仅验证了本文传感器结构优化方法的可行性, 还展示了三电极电离式MEMS 传感器在气体检测领域的巨大应用潜力.

表9 碳纳米管三电极传感器与现有NO, SO2 传感器的性能对比Table 9.Performance comparison of carbon nanotube based triple electrode sensors with the existing NO and SO2 sensors.

5 结 论

本文根据传感器的电极结构, 采用流体模型对碳纳米管三电极传感器进行了静电场及极间放电仿真建模.采用有限体积法对模型进行求解计算,仿真获得了传感器的电场分布及收集极平均收集电流密度.分别从传感器的3 个电极结构优化出发, 设计了8 种不同结构的传感器, 建立了不同结构传感器的放电流体模型; 在相同电压和温度条件下, 仿真获得了不同结构传感器的平均收集电流密度; 通过对比, 确定了最优化的传感器结构; 并制作了对应优化结构的传感器, 进行了实验验证.制作了两只不同极间距的优化结构传感器, 组成了传感器阵列, 检测了NO 和SO2气体浓度; 并与现有产品进行了性能对比, 表明优化结构的传感器具有明显的性能优势.实验结果验证了本文设计的传感器结构优化方法的可行性, 为后续传感器的新型结构设计奠定了基础.