基于系列模型试验的波流共同作用下单桩冲刷及防护措施研究
2021-05-14杨子希袁春光张华庆欧阳群安
杨子希,袁春光,张 弛*,张华庆,欧阳群安
(1.河海大学 港口海岸与近海工程学院,南京 210098;2.交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室 工程泥沙交通行业重点实验室,天津 300456)
在海洋环境中,伫立在海床上的桩柱常受到波浪、水流等动力因素的作用,产生严重的冲刷,据相关资料统计,由于海床冲刷导致结构失稳破坏占工程事故的24.6%[1]。因此海床的冲刷深度与范围是在工程设计中需要考虑的重要因素。
对于单桩的冲刷问题而言,前人已在恒定流或者波浪单独作用的条件下展开了大量研究,这方面的文献可以参考Melville[2-3]、Breusers[4]、Ettema[5]、Raudkivi[6-8]、Sumer[9-11]等。研究表明了恒定流作用时,控制冲刷深度ds的主要参数有相对水深h/D(D为桩柱直径),希尔兹参数θ,相对粒径d/D,级配σ等;波浪作用时则为Kc数及相对直径D/Lw(Lw为波长)。
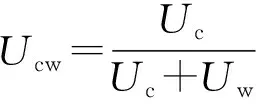
值得注意的是,上述国内外研究成果几乎集中在沙质海床,而对极细沙海床的研究成果开展较少。我国海岸工程中将粒径处于0.063~0.125 mm的泥沙称为极细沙,极细沙易起动,易沉降,且在一定动力条件下还可发生液化现象[20]。依据Sumer[11]的研究,极细沙底床的桩墩冲刷深度最大可达到沙质底床的两倍。上述结论是在波浪单独作用下得出的,参考WangRK、Eadie、李林普、袁春光等针对沙质底床的研究成果,在波、流联合作用下,其局部冲刷深度也会更大[12-13,21-22]。
本文依托粤电湛江新寮海上风电项目,采用正态系列模型与经验公式相结合的方法,旨在确定单桩结构在极细沙海床上的冲刷深度及不同防护措施的防护效果,同时验证经典经验公式在极细沙海床下的适用性,为工程设计提供参考。
1 模型设计及试验方法
对于冲刷物理模型来说,常采用动床模型或者系列模型。对于动床模型来说,如果能保证泥沙运动相似以及重力相似,则可以基本消除比尺效应,且试验周期短、成本低。然而在实际操作中,满足泥沙运动相似十分困难——通常为了满足泥沙的运动相似,要求试验模型沙粒径较细重率较小,而过细的模型沙又会带来絮凝及黏结力等一系列问题,反过来又使运动相似难以满足,尤其是对于拟建工程区域的极细沙海床,在波流联合作用下极其活跃,是常用的模型沙所难以模拟的。同时对于动床模型来说,还需要现场冲刷资料来对实验结果进行验证,由于该工程还在建设中,无法得到实际的冲刷资料,因此对于本试验来说,基于比尺缩放模型沙的动床模型很难解决问题。
对于由泥沙运动不相似所带来的结果偏差问题,一般可通过做多组几何比尺不同的试验并将试验结果外延来消除偏差,也就是系列模型方法。系列模型的优势在于可不对泥沙进行缩尺而采用原型沙当作试验沙,并且也无需实测资料为试验提供验证数据。
1.1 系列模型原理[23-25]
沙玉清假定模型试验所研究的物理量与影响这一物理量的其他变量之间存在如下指数关系
X=Khα1Yα2Zα3
(1)
式中:X为所研究的物理量,可以是冲淤深度,也可以是冲淤时间;h为深度;Y、Z为深度以外的其他水力、泥沙因素变量;α1、α2、α3分别为这些变量的指数;K为系数。这里自变量仅取3个,当有较多自变量时,也可同样纳入。
对上述方程式写成比尺关系式,其结果为
(2)
沙玉清认为系数比尺λK是由模型缩小引起的,假定它与深度比尺成指数关系
(3)
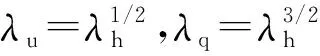
这样,上述比尺关系式将转化为
(4)
式中:α为全部水力、泥沙因素变量比尺均转化为深度比尺后的指数和。对于原型而言,λh=1,λx=1,故应有C=1,最后得
(5)
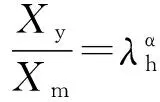
(6)
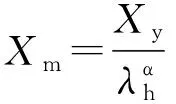
(7)
综上分析可见,当采用一定几何比尺的模型进行试验时,则λh为已知,Xm可以通过观测求得,式中的未知量尚有α、Xy两个。如果能做两个模型就可建立两个方程式,联解后便可求得Xy,或将所得Xm及λh的数据点绘在双对数纸上,连接1、2两点,与λh=1或lgλh=0的纵轴相交,交点纵坐标即为所求原型物理量的数值Xy。
当模型沙采用原型沙或者模型沙与原型沙遵循同一起动规律时,则泥沙起动流速相似比尺一般式为
(8)
在满足重力相似条件下流速比尺为
(9)
则得完全满足相似理论的正态动床模型几何比尺为
(10)
将有关参数代入上式,即可得出经系列模型延伸到比尺λh,即可得出原型情况下的冲刷深度。即当采用原型沙时,得出λh为1;当采用模型沙时,λh不等于1。
1.2 模型设计
拟建海上风电项目工程场址位于湛江市新寮岛东北面海域,水深在6~9 m(海底面高程-7.0~-11.5 m)。项目规划装机总容量为203.5 MW,拟布置37台5.5 MW单圆桩风电机组(直径为7.5 m)。本次研究的冲刷对象即为该风电基础。
在波流共同作用下近岸地区的冲刷模型应满足几何相似,重力相似,水流运动相似,波浪相似和泥沙起动相似等,同时试验沙与原型沙休止角相似,保证了冲刷坑的几何形态相似。根据该项目物理模型试验要求,考虑到实验室条件以及造波和生流能力,模型的比尺设计为30,40,50。
为了满足实际需要,试验在1:30比尺下研究了碎石以及沙被两种防护措施的效果。碎石防护采用3种方案,碎石直径依次增大,其中方案一采用d50=2 mm的碎石进行覆盖,防护层顶整体高出床面5 mm,呈椭圆形,长轴1 m,短轴0.8 m;方案二底层采用d50=2 mm碎石圆形覆盖,半径0.5 m,厚度17 mm,表层加盖厚27 mm,半径0.4 m,d50=5 mm的碎石;方案三底层采用d50=2.5 mm碎石圆形覆盖,厚度17 mm,表层加盖厚27 mm,d50=10 mm的碎石,覆盖半径均为0.5 mm。沙被方案整体呈八角形,由四块沙被搭接而成,整体长、宽均为1.2 m,厚度17 mm,布置详见2.2节。
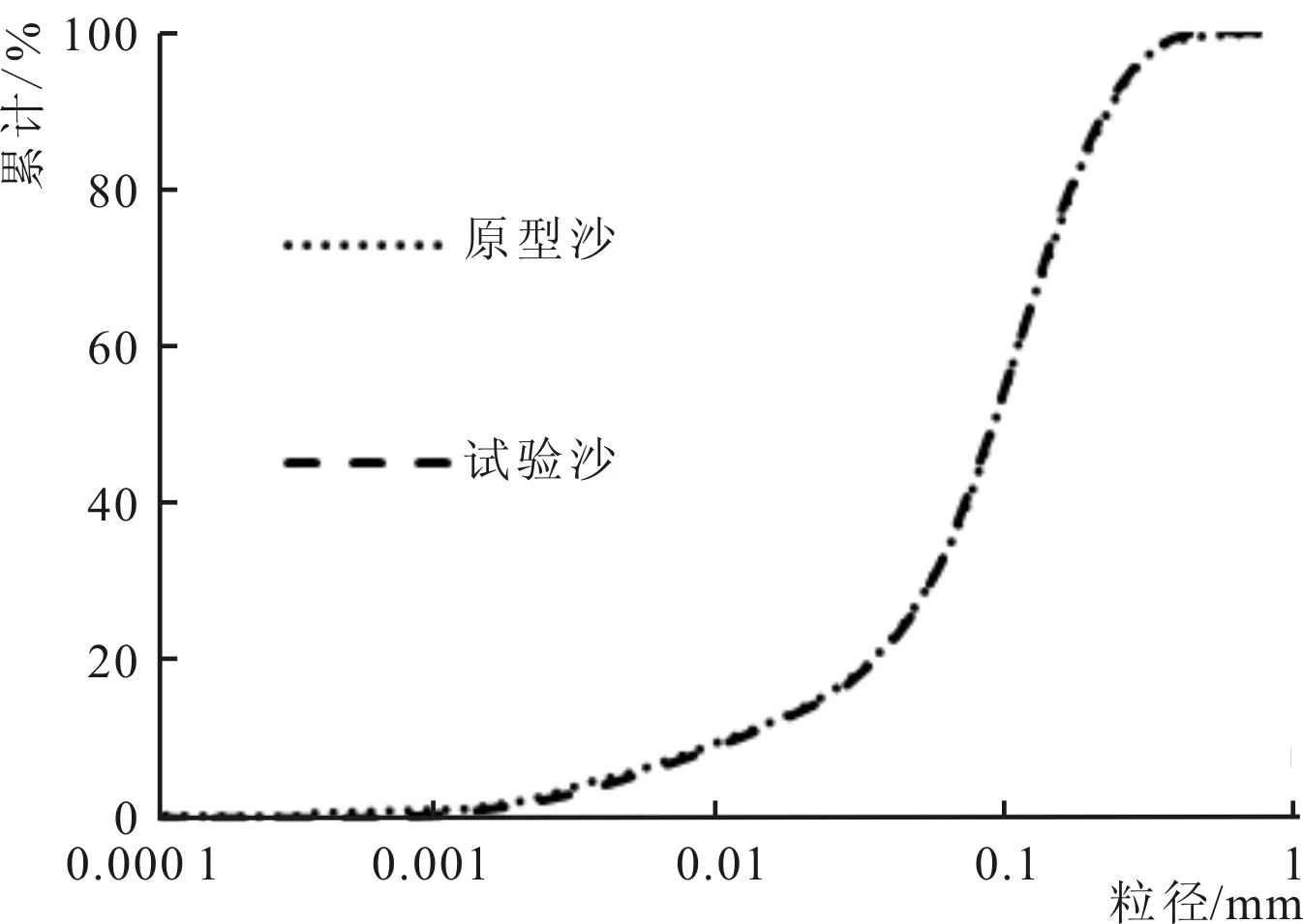
图1 泥沙级配曲线Fig.1 Size frequency curve of model sand
1.3 模型沙的选择
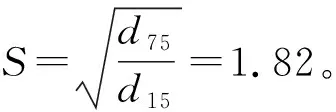
1.4 试验条件与过程
依据实测水文资料,该海域观测期最大垂线平均流速为0.93 m/s。在风电场设计过程中考虑在台风影响条件下50 a一遇可能的最大流速为2.14 m/s。风电厂址处水深在6~9 m,此处波高衰减很快,并且台风影响期间波浪已发生破碎。50 a一遇波浪+极端高水位(5.47 m,理基)作用下H13%=5.28 m,Tp=13.1 s;50 a一遇波浪+极端低水位(-0.34 m,理基)作用下H13%=3.22 m,Tp=11.8 s;5 a一遇波浪+极端高水位作用下H13%=4.82 m,Tp=10.9 s。
试验在交通运输部天津水运工程科学研究院展开,试验水槽长70 m,宽3 m,拟建模型试验段长4 m,宽2 m。海床地形按照特征实测地形制作,特征试验基础布置在模型中部。动床铺设深度0.5 m,按照系列试验最大比尺,相当于原型深度15.0 m。为了模拟对单桩基础刷最不利的情况,试验采用单向流,水流流向与波浪传播方向一致。试验工况如表1所示。
测量仪器采用Vectrino三维点式多普勒流速仪、超声波水位仪、BG-1型波高传感器及Z+F三维激光扫描仪,分别对特征点流速、流向、水位、波高地形等进行测量。同时在模型迎波面、背波面和两侧分别贴有辅助标尺,在每次试验前后分别读取标尺上的床面高度,检验三维激光扫描仪的测量精度。
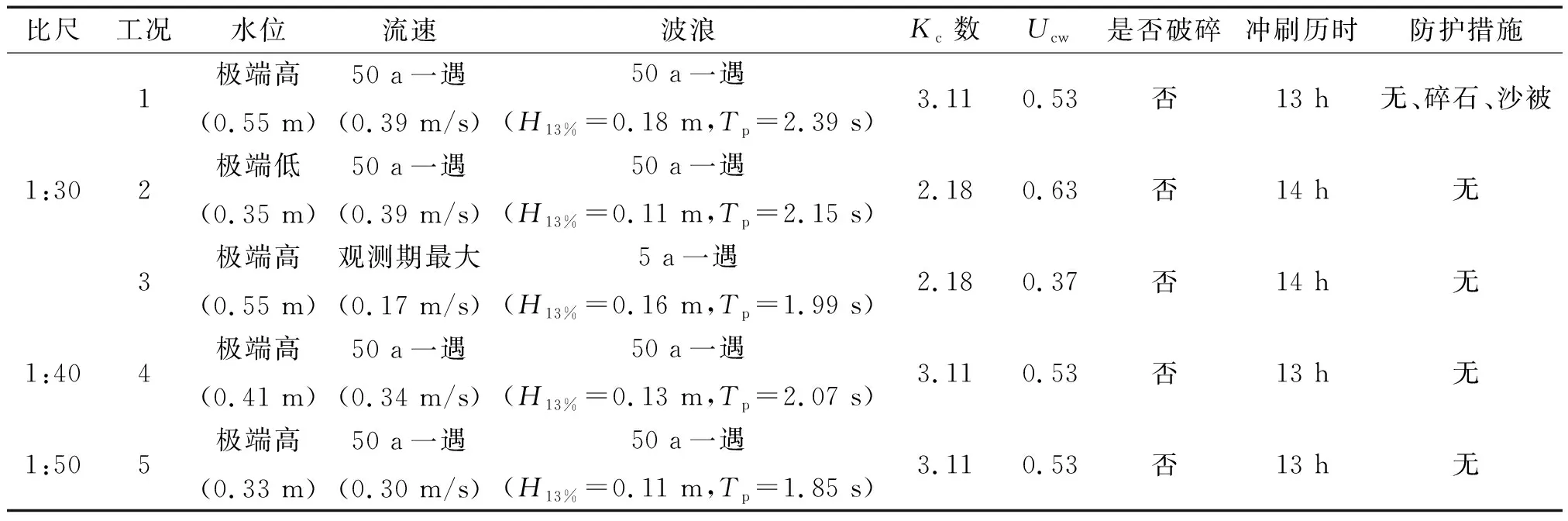
表1 试验工况Tab.1 Experimental condition

2-a 工况12-b 工况22-c 工况3图2 不同工况下冲刷坑形态示意图(单位:m)Fig.2 Schematic diagram of scour pit morphology under different conditions
2 试验结果分析
2.1 无防护下冲刷分析
2.1.1 冲刷坑几何形态
图2为不同动力条件作用后圆柱周围的冲淤情况。对于工况1、2而言,其波流动力条件较强,冲刷深度比较接近,冲刷坑形态均接近于水滴形;工况3减弱了波浪与水流强度,冲淤形态与工况1、2有明显不同,冲刷坑集中在桩两侧,而桩前、后冲刷深度与远处床面接近,无明显冲刷坑,类似于动床冲刷。这是因为随着波流强度减弱,马蹄涡的强度减弱,此时造成冲刷的原因主要是圆柱两侧的束水冲刷。
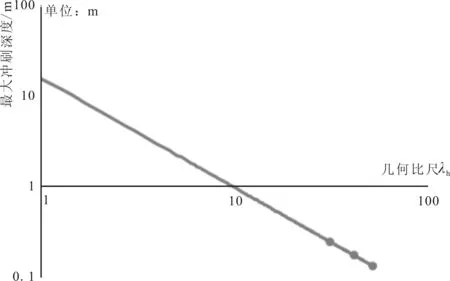
图3 系列模型延伸图(单位:m)(极端高水位+50 a一遇流速、波浪)Fig.3 Extrapolation map of the scour depth in series models
三组工况下,冲刷均最先出现在圆桩迎波面两侧夹角与轴线约呈45°处,并且随着冲刷深度的增加,冲刷坑逐渐向迎波面和背波面发展。由于极细沙易起动的特点,且实验中水流强度较大,底床泥沙起动后,直接悬扬并由水流带向下游,圆桩上下游并未观察到泥沙落淤。
2.1.2 最大冲刷深度
通过比对5组工况发现,桩周冲刷深度初期发展较快,当发展到一定阶段后冲刷减慢,逐渐达到极限深度,其中桩前及两侧冲刷深度接近,背水侧冲刷深度略小。根据1.1节方法绘制双对数曲线(图3),得到“极端高水位+50 a一遇流速+50 a一遇波浪”下单桩基础最大冲刷深度为15.09 m。
2.2 不同方案防护效果比较
图4展示了不同方案的防护效果,三组碎石防护在试验进行到2 h(模型值)后,均出现了不同程度的破坏情况,其中方案一碎石防护层破坏的最为严重。随着抛石粒径的增加,方案二、三的破坏程度逐渐减小,但对于方案三而言圆桩周围冲刷坑也深入底床,表面d50=10 mm粗碎石层的边缘发生了明显的移动破坏,底层黄色细碎石部分裸露。

4-a 碎石防护方案一(碎石粒径d50=2 mm,厚5 mm)

4-b 碎石防护方案二(表层碎石粒径d50=5 mm,厚27 mm;底层碎石粒径d50=2 mm,厚17 mm)

4-c 碎石防护方案三(表层碎石粒径d50=10 mm,厚27 mm;底层碎石粒径d50=2.5 mm,厚17 mm)

4-d 沙被方案图4 防护措施及其比较(单位:m)Fig.4 Protective measures and their comparison
对于沙被防护方案而言,当试验进行了13 h(模型值),依然起到了较好的防护效果,表现为:(1)单圆桩风电基础周围底床受到砂被的保护作用未发现冲刷现象;(2)在波流作用下,沙被各处保持完好,没有出现“掀起”或者“整体移动”现象;(3)由沙被引起的二次冲刷现象比较微弱,沙被边缘的二次冲刷深度与床面在波流作用下形成的自然冲刷深度基本一致,沙被造成的二次冲刷与床面的自然冲刷相互融合,无法区分二次冲刷坑边缘位置。
3 国内外经典经验公式计算及同类冲刷试验结果对比
3.1 国内外经典经验公式计算
国内外很多学者对波流共同作用下的大直径单圆桩基础冲刷进行了试验研究,其经验公式总结如下
(1)Sumer公式[14]
(11)
式中:ds为桩基冲刷深度;dsc为相同水深、流速条件下,水流单独作用时的平衡冲刷深度;D为直径;Vc为水流单独作用下的近底流速(可用距离底床0.5D处的流速表示);Um为波浪单独作用下近底水质点运动流速最大值;Ucw表示水流导致的流速占波流共同作用形成流速的比例;Lw为波长,该公式仅适用于动床;D/Lw<0.2的细桩。
(2)韩海骞公式[26]
(12)
式中:h为全潮最大水深;B为全潮最大水深下的平均阻水宽度;Fr为弗劳德数;k1为基础桩平面布置系数,条带型k1=1,梅花型k1=0.862;k2为基础桩垂直布置系数,直桩k2=1,斜桩k2=1.176,该式适用于潮流冲刷。
(3)Qi WenGang公式[16]
(13)
该式适用范围:0.1 (4)陈海鸥公式[27] (14) 式中:V为断面平均流速,该式适用于D/Lw>0.2的大直径桩。 (5)李林普公式[21] (15) α=0D/Lw≥0.5;α=-0.102D/Lw<0.5 该式适用于0.07 在30比尺下,5组公式的计算结果与试验值的对比见表2。综合比较上述计算结果,Sumer公式与Qi公式整体计算结果与试验值比较接近。 表2 经验公式计算结果Tab.2 Calculation results of empirical formula 目前针对单向流作用下的圆桩局部冲刷研究成果较多,但对于近岸波流共同作用下圆桩局部冲刷公式较少,有些研究只考虑到了潮流的作用而忽略了波浪的作用,波浪条件相对于水动力条件较弱时,计算结果比较接近,遇到波浪作用不可忽视时,计算结果偏差较大,例如韩海骞公式。 在其余四家具有代表性的公式中,有公式以相对直径、相对水深等作为主要水力指标,也有公式使用Kc数、相对速率作为指标。这些公式虽然考虑了波流共同作用,但它们多由试验数据整理而来,具有一定的适用范围。对于李林普、陈海鸥公式而言,其试验以相对直径D/L>0.15的大直径单圆桩为背景,而本次试验圆桩的相对直径在0.05~0.06,属于细直径圆桩,由于大直径圆桩与细直径圆桩在冲刷机理上的不同(细直径圆柱冲刷与桩前下降水流与桩周涡旋强度有关,大直径圆柱冲刷与波浪反射有关),当这些公式用来计算细直径圆柱冲刷时,可能存在较大误差。 Sumer与Qi的公式以相对速率及Kc数为主要水力指标,计算结果与试验值误差较小,一方面可能是因为试验设计的Kc数在0.4~26,涵盖了绝大多数近岸工程中可能出现的情况。另一方面在Qi的试验中,相对直径在0.02~0.08,也属于细直径圆桩冲刷。Sumer的文章中虽然没有详细的列出试验参数致使无法确定其相对直径,但通过在袁春光[17]计算发现,Sumer公式与Qi公式在预测大直径圆柱冲刷时均出现了结果为0的情况,说明Sumer公式与Qi公式都仅适用于计算细直径圆桩;李林普与陈海鸥公式在预测细直径圆柱冲刷时出现了负值,因此这两家公式也仅适用于预测大直径圆桩冲刷。 对于沙质底床,实测资料表明冲刷深度随粒径的变细而有增大的趋势,但无论是哪一家公式均未能正确反映这一现象,尤其是对于极细沙而言,其起动流速位于希尔兹曲线的底部,在波流作用下异常活跃。因此无论是相对直径、相对水深还是Kc数、相对速率均无法反映泥沙粒径和级配的影响。 (1)波流动力条件较强时,极细沙海床在波流作用下的单桩冲刷深度类似于水滴型,随着动力条件减弱,冲刷坑集中在圆桩两侧、桩前后冲刷深度接近于动床冲刷。且在三组工况下,冲刷均最先出现在圆桩侧前方,并且随着冲刷深度的增加,冲刷坑逐渐向迎波面和背波面发展。 (2)试验最不利工况为“极端高水位+50 a一遇流速+50 a一遇波浪”(Kc=3.11,相对速率Ucw=0.53),该条件下单桩基础极限冲刷深度为15.09 m,达到了风电基础直径的2倍。 (3)通过比对碎石及沙被两种防护方案,在试验设置的碎石粒径范围内,碎石防护效果不及沙被防护效果好,圆桩受沙被的保护未发生冲刷破坏,沙被也未出现“掀起”或“整体移动”现象。 (4)通过对比以往国内外学者提出的经验公式,认为应综合考虑经验公式的适用范围与实际情况之间的差别,并分析其对冲刷结果可能带来的影响趋势。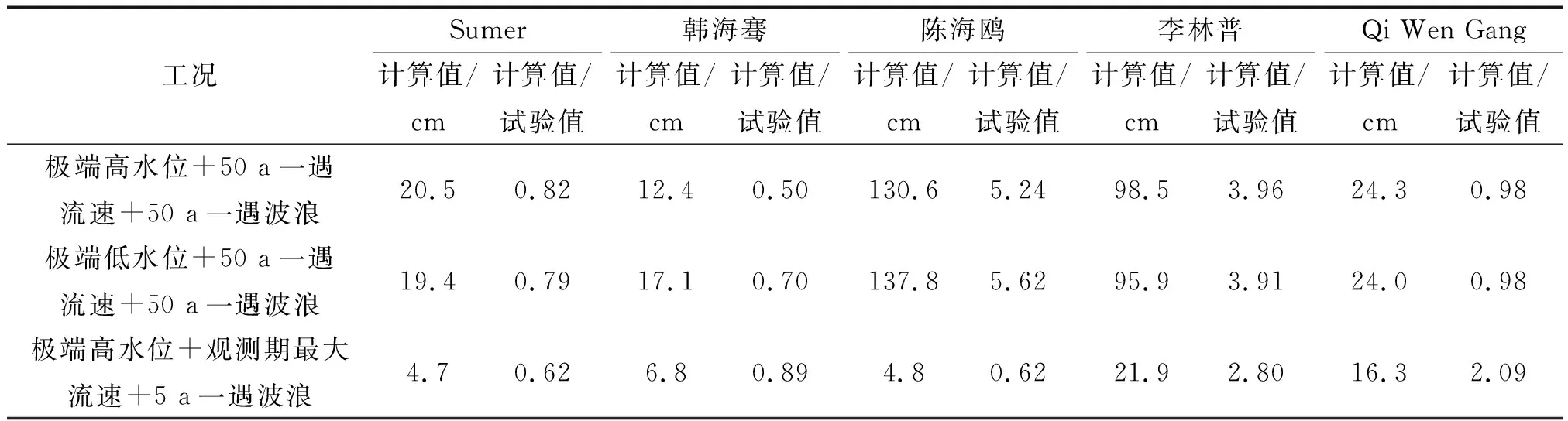
3.2 计算结果偏差分析
4 结论
