土岩复合地层条件下爆破振速衰减模型优选
2021-05-14胡鑫涛冯志威张建国司小东
朱 明, 胡鑫涛, 冯志威, 张建国, 司小东, 亓 宁
(1.青岛地铁集团公司, 青岛 266100; 2.山东正元建设工程有限责任公司, 济南 250101; 3.中交公路规划设计院有限公司, 北京 100032; 4.上海勘察设计研究院(集团)有限公司, 上海 200082)
随着中国经济的发展,城市发展进程日益加快,地下工程建设逐渐增多,采用钻爆法施工是隧道开挖最经济合理的一种施工工法。爆破法开挖施工速度相对较快,具有施工工艺简单、成本低等优点[1-3],但同时其亦具有明显的危害性,如爆破振动效应、飞石、烟尘以及噪声等,均对隧道施工及其环境效应产生不利影响。随着中国城市轨道交通的发展,地铁施工穿越城市繁华地段过程中,爆破施工产生的振动效应严重影响地面构筑物的安全性,造成经济损失及不良的社会影响[4-5]。因此,需要加强对地面爆破振动的衰减规律的预测研究。
爆破施工对城市建设产生的影响和严重事故引起了一些专家学者的广泛关注。吴波等[6]通过数值模拟和萨道夫斯基修正公式研究了隧道施工爆破载荷在不同工况条件下对周围建筑的振动特性。邓锷等[7]通过数值模拟的方法确定了顶板厚度对围岩稳定性的界限。叶宇等[8]通过数值模拟方法研究了隧道与公路相对位置不同,隧道施工对已有公路的影响。对于爆破振动强度的判别依据,不同时代、不同国家所采用的参数略有不同:以美国为代表的西方国家则经历了以峰值振速、振动加速度、振动能量分布作为标准的过程,并最终确定以振动速度作为判断标准的安全准则;中国目前将爆破峰值振速作为振动强度判断标准,并对不同的构筑物辅以爆破振动频率进行爆破振动安全评判[9]。
炸药爆炸后,部分爆破能量通过介质向外传播形成地震波,其为一种与自然地震波相似但又相区别的非常复杂的复合波,由不同幅值、不同频率与不同相位的各处波型叠加而成,是一种随机过程;地震波在传播过程中会由于爆源特性、岩土介质的性质、地形条件、爆破方法、爆源大小的不同而产生衰减现象[10-11]。目前,在爆破振动衰减规律的研究方面以经验公式法最普遍。中国目前多采用萨道夫斯基公式进行参数优化及爆破设计、振速预测[12];而萨道夫斯基公式存在一定的局限性,对于复杂地形、地层条件适用性相对较低。因此众多学者采用多种方法,充分考虑爆破振动测点高差[13]、围岩损伤[14-16]、振动频率[17]等因素,不断优化和修正经验公式,使其能更合理地预测爆破峰值振速。然而,对于爆破过程的随机性以及爆破场地差别,爆破振动速度衰减模型并未形成统一的公式,对于不同地区的爆破施工,进行爆破振动控制及预测需进行一定的模型优选与优化,以期形成最佳模型。
现以青岛地铁某暗挖车站临时斜井下穿建筑群工程为对象,依托于青岛土岩复合地层结构,对比分析修正后的经验公式模型的共同特性,利用MATLAB软件进行多元模型线性回归分析,并针对其不足之处进行模型优化、验证。
1 工程概况
1.1 工程简介
青岛地铁某车站临时斜井仅作为车站站厅层施工通道,分明挖与暗挖两段,其中暗挖段采用全断面法施工,总长为297.7 m,标准段开挖宽度为5.5 m,高度为5.8 m,设置坡度12.5%。暗挖段与车站主体连接工程下穿两条城市主干道,期间分布多幢建筑,其中包括教堂、供电站等重要构筑物,对爆破振动的控制要求较高。基本工程位置如图1所示。
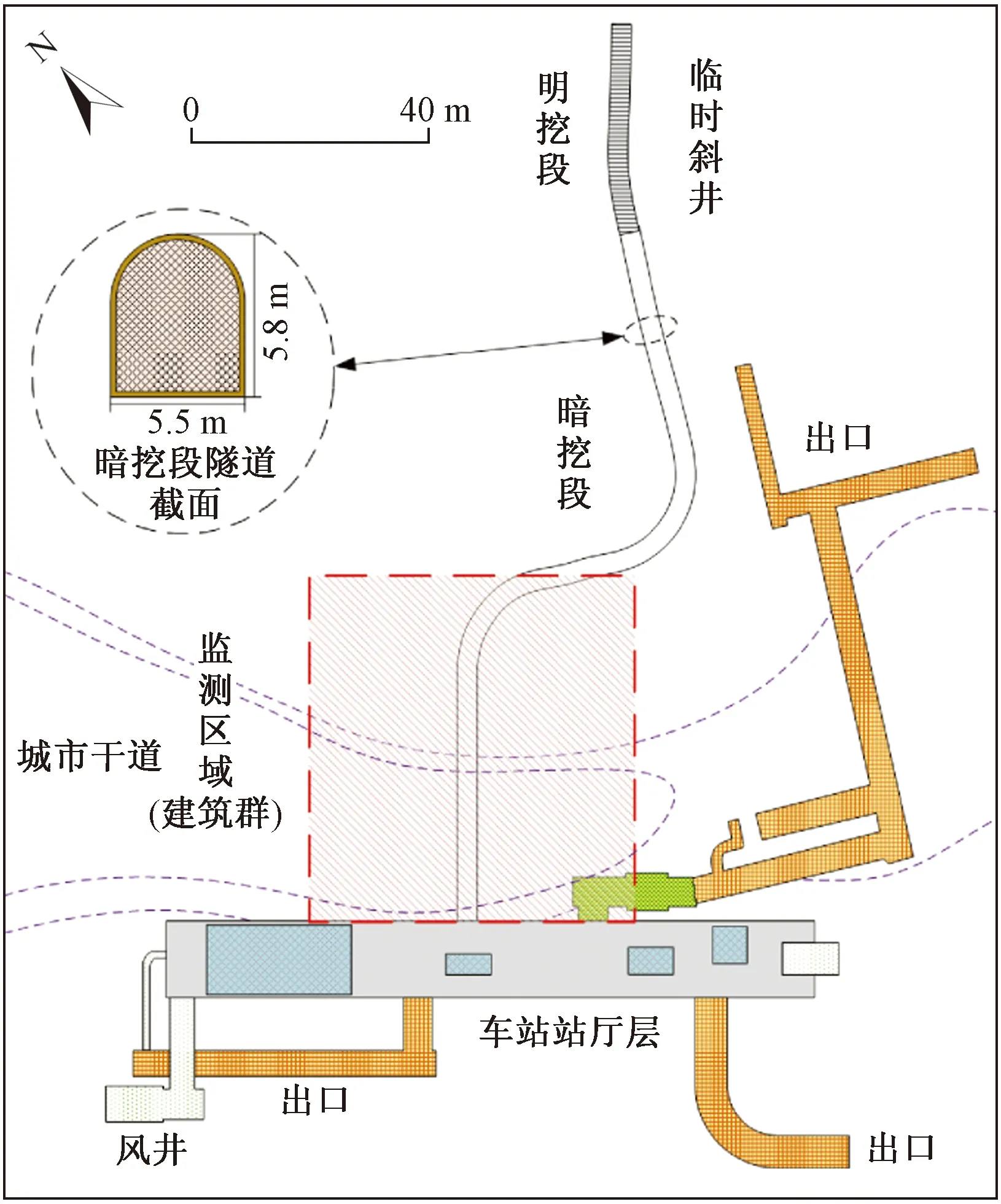
图1 工程位置
1.2 工程地质条件
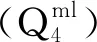
车站结构基本处于微风化岩层,构造小断裂较多,综合判定,围岩等级为Ⅲ2-Ⅲ1级,局部破碎带为Ⅳ2-Ⅳ1级。
1.3 监测点布置
爆破振动衰减规律研究的现场实测数据主要是通过TC-6850网络测振仪进行现场监测,该仪器采用最先进的智能化传感器,自带WiFi/3G/4G网络。在施工期间,为了更好地研究爆破振动的衰减规律,采用在一次爆破之后,在地面设置多个监测点进行监控和多次爆破观察一个监测点记录结合的方式,更好地研究爆破振动信号的衰变规律。选取爆破点正上方20 m处为监测点1,记录爆破振动速度,以测点1为原点,每10 m设置一个监测点,共设置11个监测点,分别为ZC01、ZC02、ZC03、ZC04、ZC05、ZC06、ZC07、ZC08、ZC09、ZC10、ZC11,从ZC01到ZC11这段距离在隧道上方,有临空面,而ZC01到ZC06这段距离为实心岩体,没有临空面(图2)。为了进一步研究埋深对爆破振动速度的影响,隧道沿12.5%坡度继续开挖,进尺长度为15 m,每5 m位置进行一次爆破,共4次爆破,同时移动地面监测点,使监测点1位于爆破点的正上方。为了控制爆破振动,下穿过程减少了最大段装药量(掏槽孔段),第1段最大爆破装药量为1.2 kg,之后每段增加0.2 kg药量。
距爆破点高程差随着与测点1相对距离的增加不断减小,而爆心距随着与测点1相对位置的增加不断增大,在了解相对位置变换规律后,通过研究不同参数的影响,研究爆破振动衰减规律,如表1所示。
2 爆破振速衰减规律
爆破振动为一种复杂的瞬态波,其影响因素众多,难以准确预测。爆破振速的衰减表现在随着距离的增加,地震波的振动强度会随之降低。研究表明,采用爆破振动速度预测更好地排除岩土因素的影响,并且与建筑物的破坏特性具有良好的相关性。因此,采用爆破振动速度来进行衰减方程的拟合具有一定有效性[18]。根据爆破振动速度衰减规律,爆破振速必然会随着时间的增加,振动速度逐渐递减。如图3所示,在极短时间内爆破振速峰值达到最高值,之后逐渐降低,体现出爆破过程的瞬时性。爆破振动速度随着相对距离的增加先增加后降低的趋势,在距离爆源最近的测点1处达到最大值。
2.1 爆破振速衰减距离效应
不同监测点与爆源的距离不同,导致在不同位置上监测点记录的峰值振速不同。选取最大段装药量为1.2、1.4、1.6、1.8 kg条件下,距离掌子面不同距离测点的爆破峰值振速平均值研究振速的衰减随距离的变化规律,如图4所示。
由图4可知,随着距离掌子面距离的增加,爆破峰值振速逐渐降低,位于掌子面顶端的测点振速最大可达1.5 cm/s,在距离掌子面0~20 m范围内,振速的衰减率最大,可达50%以上;且随着单段最大爆破药量的增加,爆破峰值振速逐渐增加,但整体的衰减规律一致,说明装药量对爆破振速的衰减影响不大,仅对其振速大小有影响。
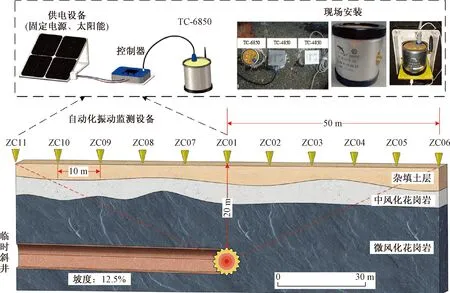
图2 监测设备布置

表1 不同测点的基本参数值(爆破药量为1.2 kg)
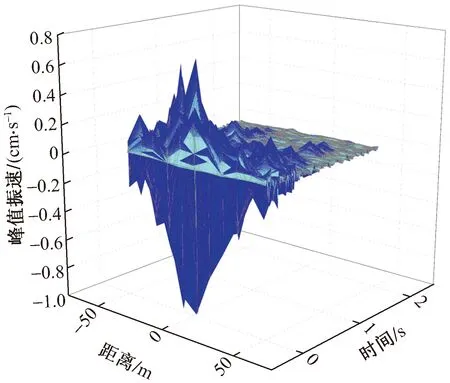
图3 峰值振速随时间和距离变化的三维图
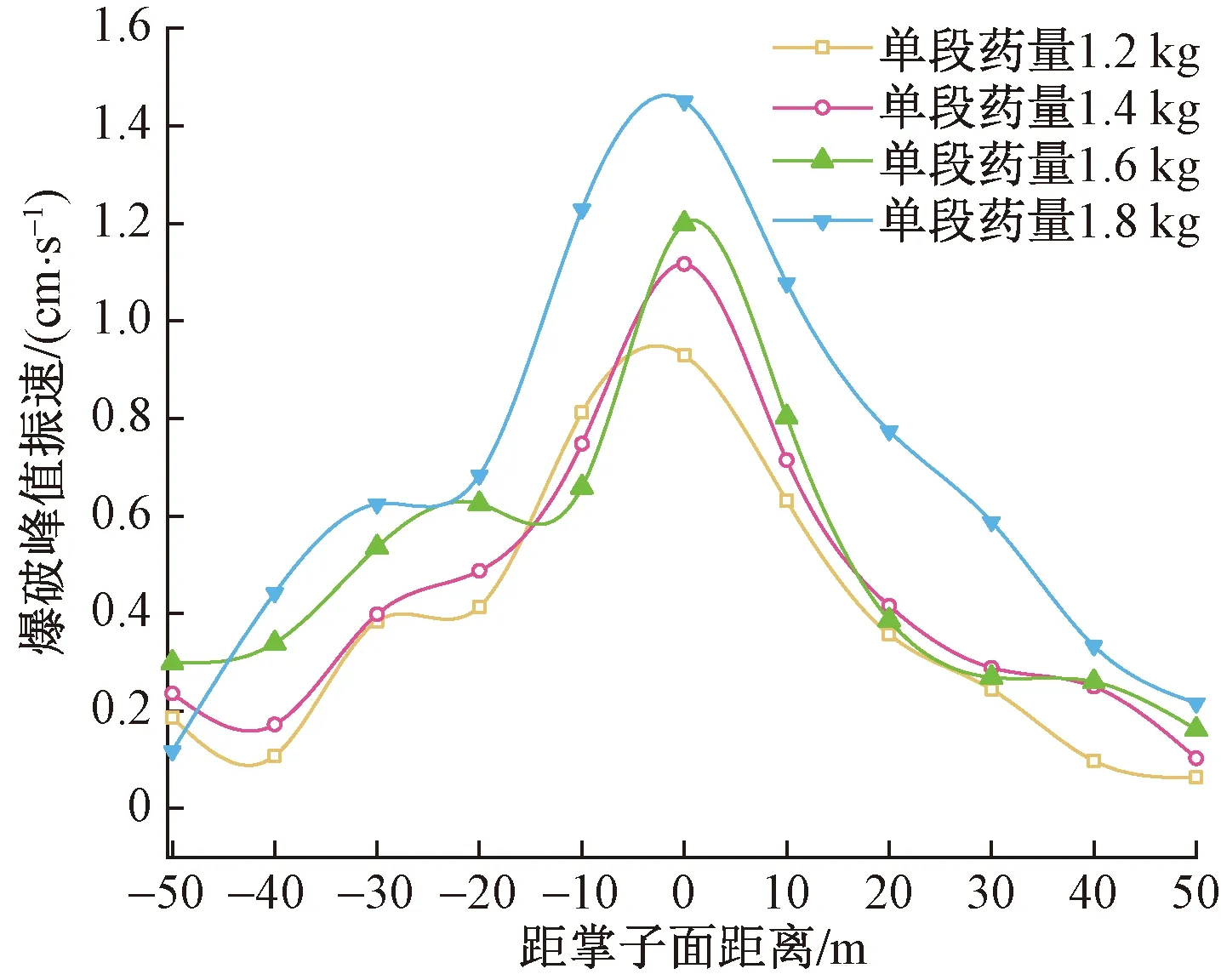
图4 峰值振速随相对距离的变化
2.2 爆破振速衰减埋深效应
埋深与地表地形密切相关,本次检测的地表起伏不大,但斜井是按照坡度为12.5 °的角度开挖,因此,地表不同监测点的埋深不同,地形的起伏使爆破应力波的能量转换,对爆破振速有一定的影响。收集每开挖进尺10 m时掌子面顶端测点的峰值振速,分析不同装药条件下峰值振速的大小情况,如图5所示。
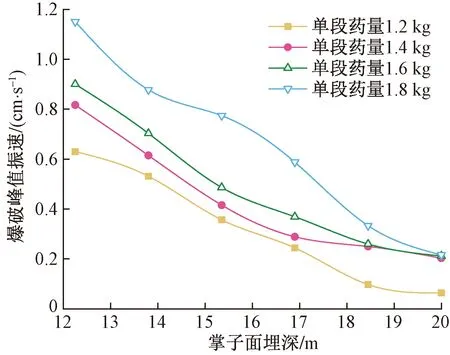
图5 峰值振速随高程差变化曲线
由图5可知,随着掌子面埋深的增加(及测点与爆心的相对高差增加)爆破峰值振速逐渐降低,且较为平缓,未出现较大波动,说明爆破振速的衰减与高程差有关,但就本次试验测试而言,其影响相对不大。
2.3 爆破振速衰减空洞效应
由于隧道在掘进过程中掌子面前后方地层不同,导致在掌子面后方受隧道开挖产生空洞效应,使地表监测掌子面前后的振动速度不同,存在区域性比变化的特点。主要表现为已经开挖的隧道振动速度比为开挖的振动速度大,为爆破振动空洞效应的主要特征。本次试验以掌子面为对称面,两侧各等距离选取10个监测点,采集10次峰值振动速度,取均值所得结果如图7所示。
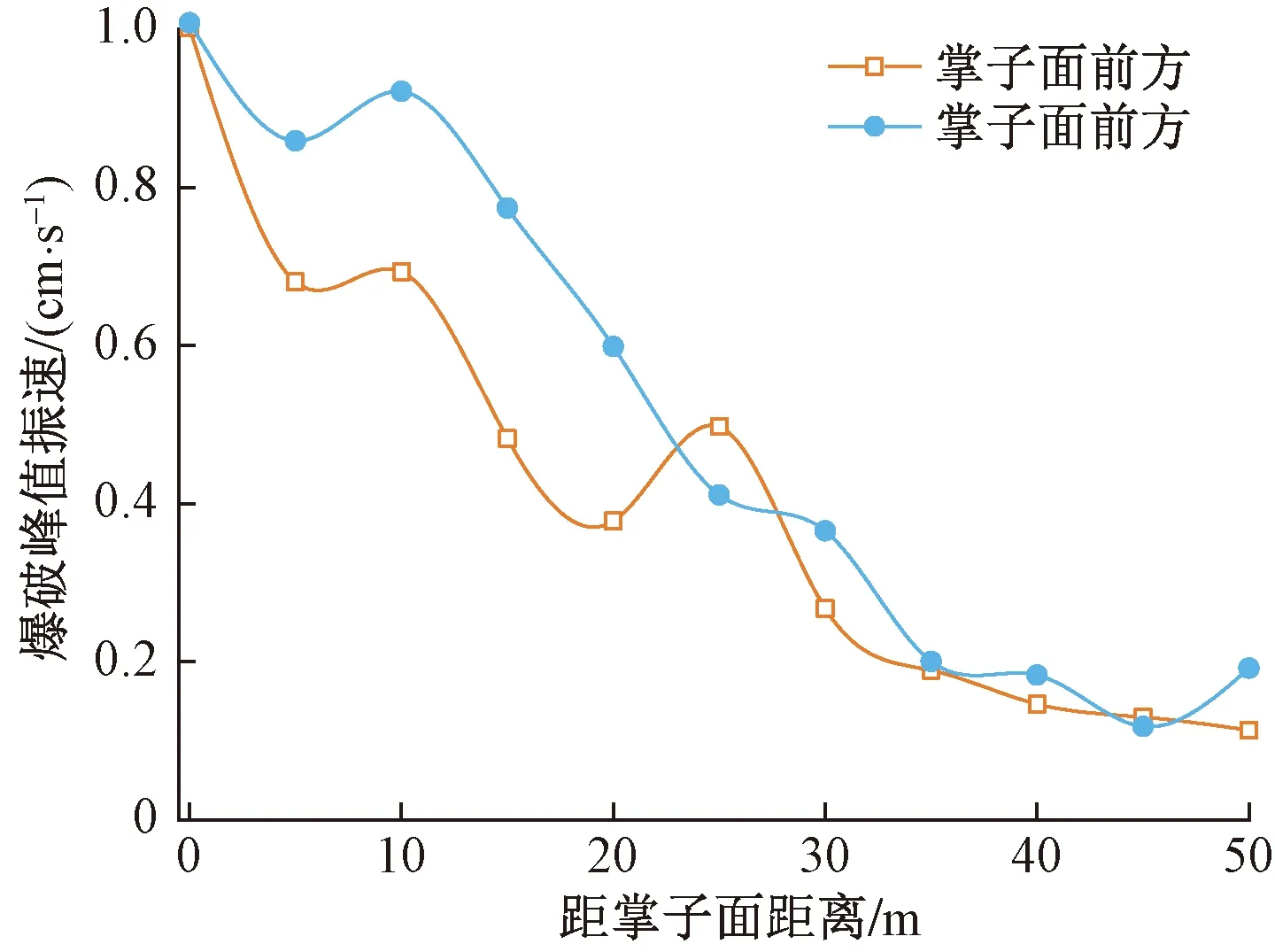
图6 掌子面前后不同距离的峰值振速变化图
由图6可知,掌子面前后的爆破峰值振速大小存在明显的差异;掌子面后方的峰值振速相对于等距离的掌子面前方测点具有放大效应,放大率在0.26~1.57;且在4~5倍洞径范围内放大效应明显,而在传播远端,放大效应逐渐消失。
3 爆破振动衰减模型优选
影响爆破振动速度的因素较为复杂,且不同因素对爆破振动的作用机理不同,因此爆破产生的地震波能量衰减具有一定的随机性和不可控性。由于不同爆区的地质环境/已有建筑物和施工条件不同,目前在爆破振动衰减规律的研究方面,还没有形成更为完善和统一的爆破振速衰减预测模型。根据前人的研究,爆破振动的影响因素大致分为炸药特性和爆破药量、传播距离、传播区的地质结构特征3类。由于爆破振速是由多种因素综合作用的结果,因此,在进行爆破振动优选时应根据不同的爆破因素选择合理的爆破振动参数,这样才能使爆破衰减模型更适用于工程建设。
将爆破峰值振速作为爆破振动强度的评价,一方面符合工程实践,另一方面亦与中国现行的《爆破安全规程》相适应。为了准确地进行爆破振动强度的预测分析,需要对各因素进行一定程度的简化。
(1)炸药特性的简化:对于某一工程而言,为了工程的可控性,其所采用的炸药性质差别不大,仅有的差别为装药的差异。
(2)地质条件的简化:对于单测点情况下,其小范围的地质、地形状况差别不大,仅须考虑本区域内的地质、场地参数。
3.1 爆破振动速度衰减预测模型
经验公式法以爆破振动速度衰减经验公式为基础,根据爆破振速与爆破参数因素之间的关系,求解一定位置爆破峰值振速,从而得出爆破振动衰减规律。这种方法应用便捷、适用性与操作性强,是爆破工程中应用最广泛的方法。中国主要采用的是萨道夫斯基经验公式,即
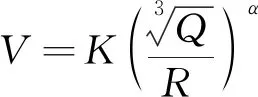
(1)
式(1)中:V为质点振动速度,cm/s;Q为单响药量(齐发爆破时为总装药量,延发爆破时为最大一段装药量),kg;R为质点到爆源中心的距离,又称爆心距,m;K、α为爆破方法、地质、场地条件等因素有关的待定系数,又称K为场地系数,α为衰减指数。
根据萨道夫斯基经验公式采用最小二乘法求出K=120、α=1.8,之后根据求得的关键参数求出不同爆破药量爆破振动衰减速度,得到基于萨道夫斯基经验公式的爆破振动速度衰减预测模型(图7)。
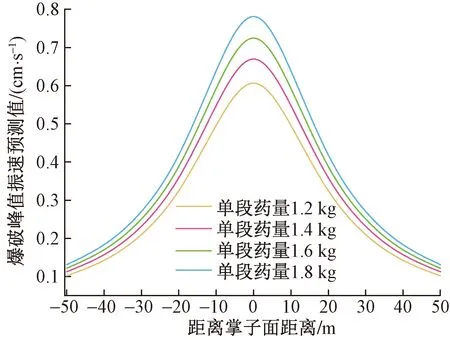
图7 基于萨道夫经验公式爆破振速预测模型
其他国家也以萨道夫斯基经验公式为基础,根据本国的具体的地质和施工条件对爆破振动衰减模型进行了修正,常见的爆破衰减预测回归模型如表2所示。
由表2可知,各预测模型公式的基本形式相似,其共同形式可写作为
V=KQmrn
(2)
式(2)中:V为爆破振动峰值速度;m/s;K、n、m为与爆破方式、地质条件以及场地状况有关的参数;Q为单段最大起爆药量,kg;r为爆心距,m。
基于萨道夫斯基经验公式修正后的预测模型的共同形式,求出待定系数K=265、m=-2.11、n=1.93,基于这个与爆心距相关的模型,求出爆破振动速度预测模型(图8)。
以萨道夫斯基公式为基础的预测模型,在地层起伏变化不大,较平整的地形条件下的精度相对较高,而对于地形地貌变化较大的地区仍采用这种模型,精度就会大大降低,之后不同学者为了提高模型预测精度,在模型中引入高程差这一参数,研究不同参数对爆破峰值振速的影响,如周同龄等通过研究爆破地震波在有高差存在的岩层中传播特征,提出了一个关于爆破质点振动速度的公式,即
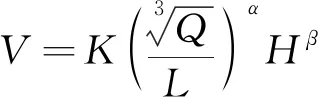
(3)
式(3)中:H为测点与爆源之间的高程差,m;L为测点与爆源之间的水平距离,m;α、β为与高程差有关的系数。
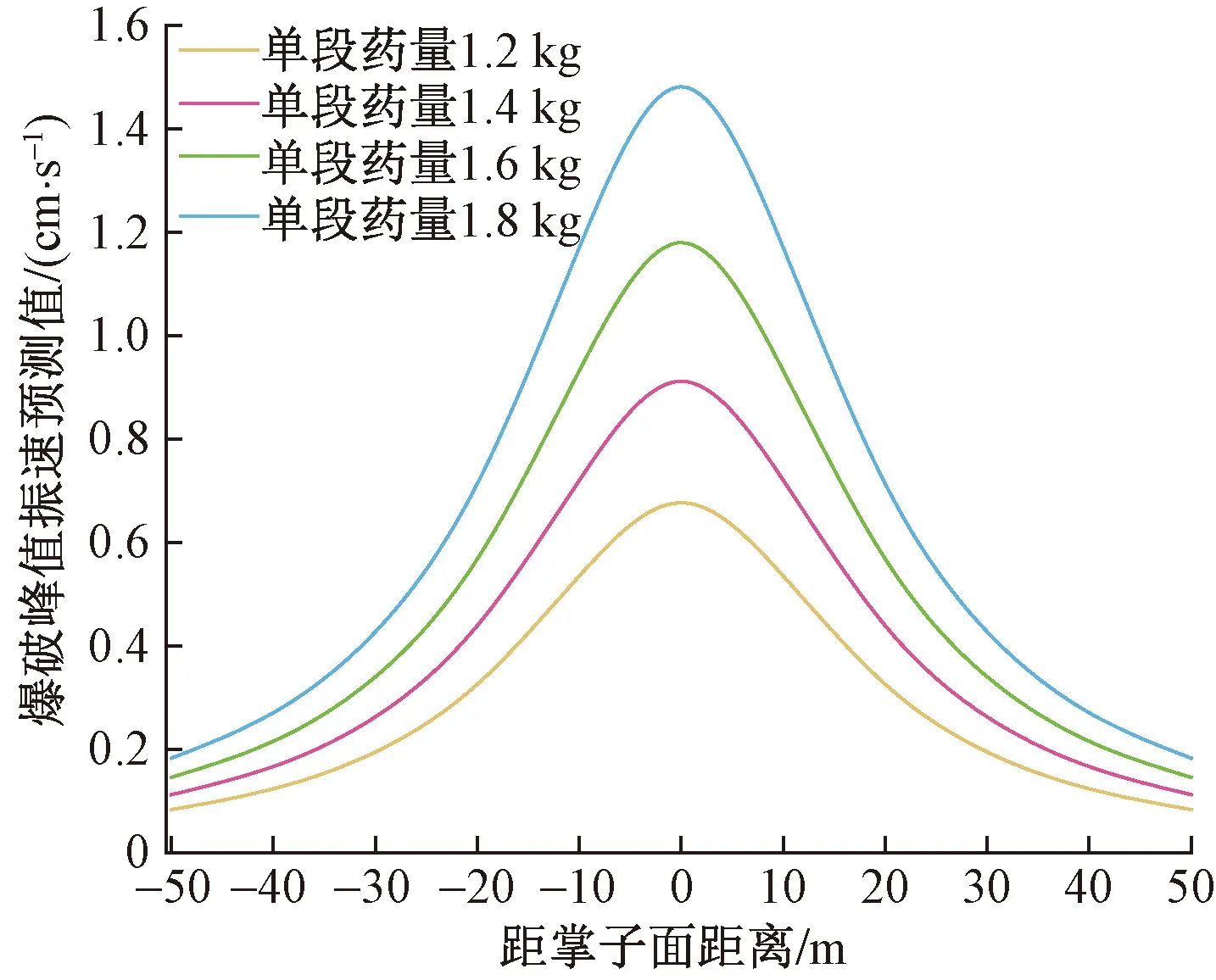
图8 共同形式的爆破振动速度预测模型

表2 常见的爆破振动强度预测回归模型
王在泉等[19]认为爆破振动衰减过程中坡高的放大效应,结合实际工程验证,提出质点振动速度公式为

(4)
唐海等[20]采用无量纲分析方法,推导反映地表变形起伏较大时,高程的放大效应公式为
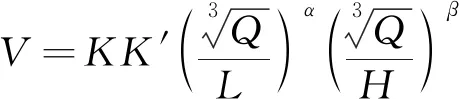
(5)
式中:K为场地系数;K′为地貌影响因素;a为衰减系数;β为高程差影响因素。
根据上述学者对于高程放大效应的研究发现:引入高程差的爆破振动速度的公式的共同形式为
V=KQmLnHi
(6)
式(6)中:m、n和i为与爆破药量高程差有关的系数。
利用最小二乘法求得K=2.37×10-6,m=1.93,n=-0.05,i=4.15,由此可得爆破振速预测结果如图9所示。
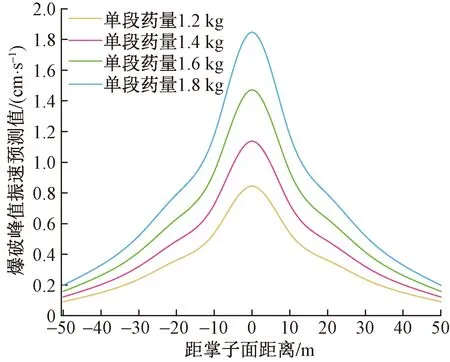
图9 考虑高差的爆破振速预测模型
整体上,3种模型随距离的变化趋势一致,都是随着与爆源距离的减小,峰值振速逐渐增高,并且随着爆破药量的增加,峰值振速逐渐增加。
3.2 模型优选
常见的爆破振动速度预测模型是基于萨道夫斯基经验公式进行修正根据不同的地质环境和施工条件选择修改部分参数。总结来说,包括两种预测模型,一种是考虑爆破药量和爆心距的预测模型,第二种是考虑爆破药量和高程差的爆破预测模型,这几种模型都能预测爆破振速,但针对不同的地质条件模型的适用性和精度不同,为了更好地优选模型,将这两种模型和萨道夫斯基经验公式与实测数据进行对比(表3、图10),分析模型和实测数据之间差异。
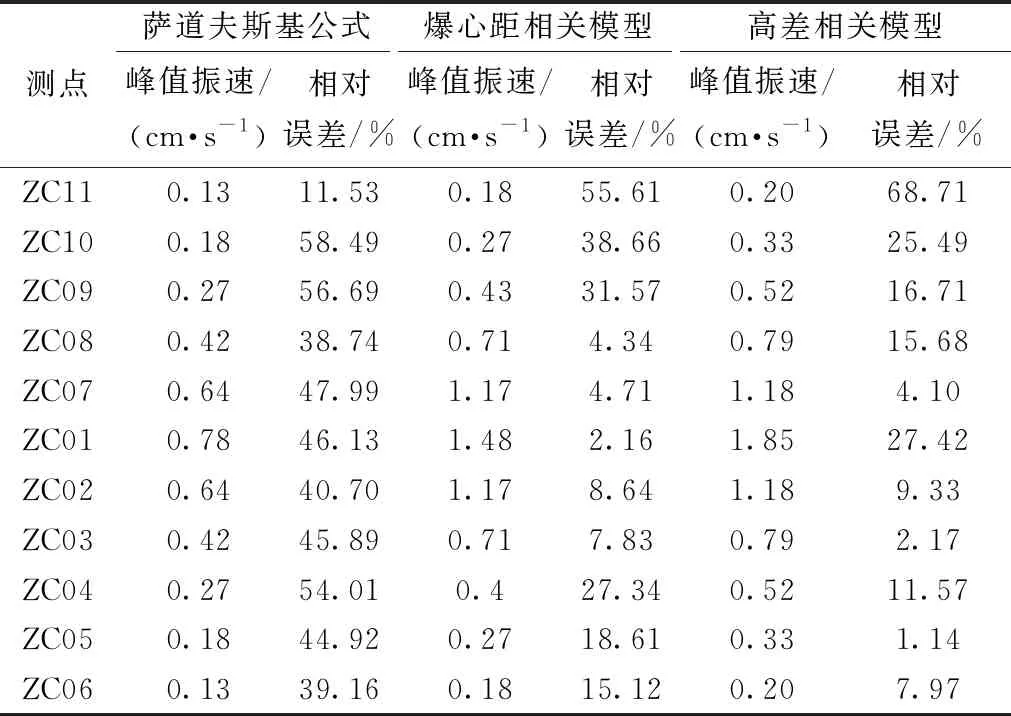
表3 模型预测数据与实测数据对比(单段药量为1.8 kg)

图10 3种爆破振速预测模型与实测数据对比
通过数据分析,可以得到以下结果。
(1)对比3种模型与实测值之间的峰值振速发现,萨道夫斯基经验公式预测值与实测数值相差较大,不同监测点的平均误差值达到44.02%,经验公式通用形式与高差相关公式的预测值与实测数值相差较小,平均误差值分别为19.51%、17.30%,就预测值的准确性而言,经验公式通用形式与高差相关公式远比萨道夫斯基经验公式更有优势,但由于本次试验场地的限制,使高差的影响不大,使经验公式通用形式与高差相关公式的准确性相差不大。
(2)对比3种模型的曲线形态可知,萨道夫斯基经验公式的曲线过于平缓,对于掌子面附近爆破振动突变型反映不佳;经验公式通用形式、高差相关公式的数据变化趋势与实测数据相近,更贴近实测爆破振动的实际情况,但高差相关公式对于掌子面顶端的预测明显大于实测数据,更能体现数据的变化率,因此相对而言,高差相关公式能更好地反映爆破振动的衰减规律。
(3)3种模型对于掌子面前后的爆破振动的差异性分布反映不佳,3者掌子面前后误差差距高达10%以上,因此3者对于空洞的放大效应不能进行预测。
3.3 模型优化
为实现预测模型对爆破振动地面衰减效应的反馈,在高差相关公式的基础上,建立分段预测模型,掌子面后方引入空洞效应影响参数λ,用以突出空洞对于爆破振动的放大效应。
通过现场试验测试,收集近200组数据,发现掌子面后方的爆破振速为掌子面前方相同距离的1.2~1.8倍,4~5倍洞径范围内放大倍数呈非线性规律,因此根据实测数据,λ可拟合为

(7)
式(7)中:a为测点与掌子面之间的水平距离,m,定位位于掌子面前方时为正,位于掌子面后方时为负。
根据式(7)以及a的取值分布可建立分段预测模型。
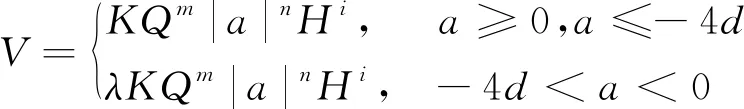
(8)
式(8)中:d为开挖洞径,m。
将实测数据与式(7)所得结果进行对比分析,所得结果如图11所示。由图11可知,优化后的分段预测模型能较好地贴合掌子面前后的爆破峰值振速差异分布;整体的相对误差在10%以内,预测效果较好。
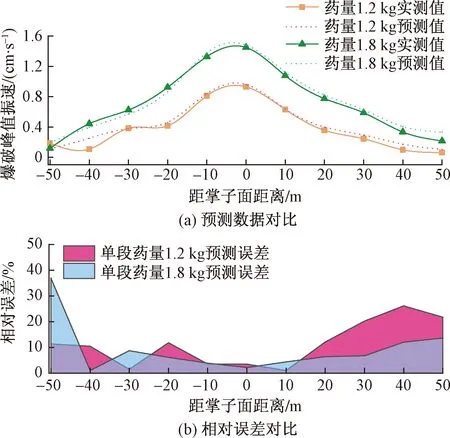
图11 优化预测模型与实测数据对比
4 结论
以实际工程为例,采用现场检测数据与模型验证相结合的方法,对比分析了不同模型的适用性,分析基于萨道夫斯基模型的修正公式的通用公式优势与不足,并进一步优化了爆破振速预测模型。通过以上研究得出以下结论。
(1)爆破振动地面衰减过程中空洞效应的影响较大,掌子面后方的爆破振速为掌子面前方相同距离的1.2~1.8倍,4~5倍洞径范围内放大倍数呈非线性分布规律。
(2)爆破振速衰减规律是多种因素共同作用的结果,仅通过一种参数的变化无法更好地反映爆破振速的变化规律。
(3)基于萨道夫斯基经验公式的修正公式总结出两个通用公式,通过与实测值进行对比,高程差相关的模型更能反映爆破振速的衰减规律。
(4)基于空洞效应以及经验参数建立的分段预测模型,能较好地反映爆破振动的地面传播的空洞效应,能有效预测爆破振动衰减规律,可为类似工程提供借鉴。
