一种在覆盖层上建造拱坝新措施的可靠性分析

陈玉琳， 毛海涛，*， 侍克斌， 王晓菊， 王 璠

(1.新疆农业大学水利与土木工程学院， 乌鲁木齐 830052； 2.重庆三峡学院化学与环境工程学院， 万州 404100)

中国西南山区河道多而水电能资源丰富，部分坝址所在地形适合建造拱坝但却位于深厚覆盖层上，给拱坝的建造技术带来了困难[1]。完全开挖深厚覆盖层建造拱坝，开挖量大，工期长且不经济，在施工导流、道路运输等方面也会带来困难。《混凝土拱坝设计规范》(SL 282—2018)规定，“坝基的开挖深度和利用岩体，应根据拱坝对坝基的承载要求和处理的效果等综合条件研究决定，高拱坝可开挖到Ⅱ-Ⅲ3类岩体，局部可开挖到Ⅲ2类岩体。”[2]此规定说明对于拱坝坝基处理一般均需要开挖至较好的岩体。相对级别高的大型拱坝，中小型拱坝如果完全依照规范，在建设条件、技术保障、资金投入等方面往往事倍功半。因此，对于一些中小型拱坝来说，需要探索更加合理的坝基处理方法和技术。

近年来，部分学者对不开挖深覆盖层上建造拱坝的坝基处理技术做了如下研究：丁莳娟[3]就窄巷口水电站，采取了在深达27 m覆盖层上跨河修建实腹拱桥，桥上修建双曲拱坝的双拱坝结构，并以双排混凝土防渗作坝基处理的方式。李仁鸿[4]就长河坝水电站实际情况，采用“拱”形垫座局部置换深达87.1 m的河床覆盖层，将拱坝置于垫座之上，并对垫座下河床覆盖层范围设置两排防渗墙进行坝基处理。田晓卿[5]就坝基覆盖层深达37.5 m的乌图河水电站，采用混凝土拱坝坐落于拱桥，塑性混凝土防渗墙作坝基处理防渗，对基础面进行固结灌浆。但国内在深覆层上修建拱坝的情况仍相对较少，遇到大量深覆层，如果能处理好上述问题并具有可推广性，仍是个难题。

针对不开挖深厚覆盖层，坝基采用若干地下连续墙(兼做防渗墙)联合高压旋喷桩的技术方案，针对独特案例(已建工程金盆电站拱坝)进行多场耦合数值模拟和监测研究，对其运行后的位移、应力进行系统分析，研判该方案的可行性和可靠性，以期为不开挖覆盖层建造拱坝提供一种新方案和技术支持。

图1 坝址剖面

1 工程概况

金盆拱坝位于中国重庆市巫溪县境内，为后溪河干流第二级引水式电站。后溪河自西向东流经坐落雁鸭溪沟口上游约320 m处坝址，河谷呈“V”形，河床宽10～30 m。坝址以上流域面积363.4 km2，水库正常蓄水位430 m，库容404万m3，死水位425 m。两岸基岩大多裸露，右岸成多级平台，河床段为第四系全新统冲洪积砂卵砾石，属强透水性。坝址横剖面如图1所示。

1.1 不开挖方案

1.1.1 不开挖覆盖层的原因

在大坝基础的处理中，顾于左岸实施导流隧洞，如果将河床大坝基础开挖至软弱、风化程度较小的基岩，则上游和下游的围堰将置于导流隧洞出口之外且难度较大，在枯水时期，很难完成大坝基础的开挖在河床以下浇筑混凝土[6]。此外，又考虑到低拱坝对河床断面基础要求略低，根据现场地质实况，坝基中砾石漂石粒径较大，属强渗透层。因此，受当地地形和地质条件的限制，决定采用新型的不开挖覆盖层的技术方案。

1.1.2 技术方案

基于以上原因，金盆拱坝在扩大基础范围内采取了从上游到下游厚度均1.2 m的3道防渗墙联合高压旋喷桩的方式进行坝基处理。墙底埋入基岩1.5 m以上，防渗墙与大坝之间采用刚性连接，防渗墙顶部插入大坝扩大基础底面以上50 cm并与扩大基础整浇，如图2所示。

河床防渗墙之间的砂石基础采用三管法施工，高压喷射灌浆分两步进行。它以梅花形状布置，注浆孔的间距为1 m，行间距为1.5 m，如图3所示。高压旋喷浆的施工参数如表1所示。

图2 基础处理横剖

图3 防渗墙与高压旋喷布置

表1 高压旋喷灌浆技术参数

2 数值模拟

2.1 耦合理论

2.1.1 流固耦合过程

假设可变形多孔介质中流体的流动服从达西定律，则可得到多孔介质中流体的连续性方程组[7]，即

(1)

式(1)中：εp为孔隙率；Qm为质量源项，kg/(m3·s)；S为单位贮存量，1/L；k为渗透系数，m/s；ρf为流体的密度，kg/m3；u为流量矢量，m/s；μ为动力黏滞度，Pa·s；p为流体的压力，Pa；χf为流体的黏动系数，1/Pa。通过式(1)，把多孔介质中的流体运动与介质孔隙率及渗透系数相关联，再经质量守恒定律，将由水头产生的水压力同固体的体积应变相联系[8-9]，表达式为

(2)

式(2)中：H为水头，m；εvol为多孔介质体积应变；αB为Biot固结系数；Sα为多孔介质存储系数。多孔材料孔隙部分包含孔隙压力、应力与应变，三者之间的本构关系为

(3)

式(3)中：αB为Biot固结系数；Pf为孔隙水压力，MPa；C为弹性矩阵；E为单位矩阵；σ为柯西应力张量；ρav为平均密度，kg/m3、ρf为流体密度；kg/m3、ρd为固体的密度，kg/m3；ζ为多孔介质中流体的含率变化大小。

流固耦合中固体体积变化Pm的表达式为

(4)

Pm根据应力张量σ计算得到，而应变张量的迹可看作体积应变εvol的变量值大小，在同时刻中，于流体而言，P、εvol、Qm为变化量。外部变量P为自变量，其余为因变量。

对于固体，σ为因变量，Pf与εvol为自变量，而Pf受ΔQm与εvol影响，产生应力张量与孔隙应变和流量变化之间的关系，引入式(4)，以获得固体颗粒的体积变化，下个时刻，各向同性项输入的附加为应力张量，可看作是耦合过程的下一个阶段的初始压力，也适用于时间相关的流动模型[10]，即

pt1=pt0+σ

(5)

式(5)中：pt0为初始应力；pt1为下一时刻的应力。在流固耦合过程里中间参数采用应力张量，在流动时间尺度上研究时，可以假设当流动状态改变时固体将立即达到新的平衡[11]。

2.1.2 应力-位移三维模型

根据拱坝的实际三维形状对坝体模型进行COMSOL建模。基岩拦截范围：沿河，沿上游和下游延伸250 m；向左右岸两侧延伸100 m；在垂直方向上截取坝顶高程的上边界，下取边界到坝底以下150 m。网格单元模型统一使用四面体单元(10节点次级单元)，单元共114 751个，结点16 997个。网格剖分如图4、图5所示。

图4 模型整体网格

图5 坝体网格划分

2.2 建模参数

该坝为抛物线双曲变厚拱坝，体型基本参数如表2所示。基础材料具体参数取值如表3所示。

表2 坝体型基本参数

表3 基础及材料物理力学参数

3 结果与分析

3.1 坝体的应力

3.1.1 坝体拉应力分布

坝体上、下游面所受拉应力三维分布(不同颜色分别代表坝体不同位置对应的各拉应力大小)具体位置及大小分布如图6所示。坝面具体应力分布如图7所示。

图6 坝体的拉应力

图7 坝面应力分布

由图6、图7可知，上游坝面的拉应力总体表现出随着高程的增加而逐渐减小，最大拉应力出现在闸孔边角、坝身泄水孔周围及拱座底部与防渗墙地基接触处。封拱前独立坝段上游坝面最大拉应力值为0.05 MPa，计算模拟坝体最大拉应力值为 0.6 MPa，其他部分拉应力值相比较小。如在高程414 m处上游坝面拉应力最大值为0.54 MPa(位于坝体泄水孔周围)，原因是在上游水压作用下，有一定的倾覆趋势，但仍在允许范围内。

同理，下游面拉应力也随着高程的增加而逐渐减小。封拱前独立坝段下游坝面最大拉应力值为0.1 MPa，拉应力计算模拟值在高程423 m处拱冠梁周围是最小的，为0.08 MPa；最大拉应力值为 0.6 MPa(位于坝体底部靠近坝轴线)。

3.1.2 坝体压应力分布

坝体上、下游面所受压应力三维分布(不同颜色分别代表坝体不同位置对应的各压应力大小)具体位置及大小分布如图8所示。

图8 坝体的压应力

据图7、图8可得，上下游面压应力主要集中在大坝中间两座闸墩附近，而坝踵、坝趾部位反而会出现拉应力。封拱前独立坝段下游坝面最大压应力值为1.56 MPa(位于坝体泄水孔周围)，在坝基高程400 m处最大压应力值为1.17 MPa(位于坝体底部靠近坝轴线)。下游面最大压应力值为1.79 MPa(位于坝体右拱部位)，在高程418 m处坝体左拱部位下游面最大压应力值为1.67 MPa。综上，坝体整体应力极值情况如表4所示。

由表4可知，在封拱前独立坝段上、下游坝面最大拉应力分别为0.05 MPa和0.1 MPa；最大压应力分别为1.56 MPa和1.79 MPa。坝体中部较大区域内上、下游面均处于分布均匀的受力状态，坝体和垫座的应力分布规律合理，在仅靠坝体自重作用下，满足坝体应力规范的要求。

表4 坝体应力成果汇总

3.2 坝基防渗墙的应力

3.2.1 防渗墙拉应力分布

通过金盆拱坝三道防渗墙三维模型情况来反映坝基所受应力分布，防渗墙拉应力如图9所示。

图9 防渗墙的拉应力

由图9可知，云图上3道防渗墙凸向上游布置，防渗墙上游面所受拉应力第3道(由左至右)顶部拉应力为0.8 MPa。第1道(由内至外)防渗墙下游面所受拉应力在顶部最大，应力值为0.55 MPa。

3.2.2 防渗墙压应力分布

防渗墙下游面压应力如图10所示

图10 防渗墙的压应力

由图10可知，防渗墙上游面压应力主要集中在第3道(由左至右)，而防渗墙底部下游面所受压应力较明显，第3道墙体底部压应力最大，应力值为7.0 MPa。

综合图9、图10分析，防渗墙体所发生的水平位移较小，应力以自重应力为主要特征。中间墙体承受压力，但其对拱座有一定支撑作用，可有效减小拱座中部挠度，加强了坝体的整体稳定性。

3.3 坝体变形

3.3.1 表面位移分布

大坝坝体表面位移分布如图11所示。

图11 坝面位移分布

由图11可得，坝体中面径向位移在水平方向上均有中部向两端递减，最大水平位移值均位于拱冠梁处；在竖向上位移自下而上随高程的增大而增大。如坝基高400 m处最大水平位移值为2.48 mm，而坝顶高程433 m处其最大值为6.10 mm。

同理，坝体中面竖向位移(拱冠梁部位)自下而上随高程上升而递增。左、右拱端最大值均位于高程423 m，分别为0.34、0.53 mm；最小值均为0.01 mm，位于高程418 m和433 m处。

4 监测数据验证

4.1 监测布置

整体监测系统包括水平与垂直位移监测[12-13]。水平位移是通过拐角的前交叉法进行的大坝顶部设置6个位移标点，分别位于拱顶，左右岸1/3拱环和左右拱端等，利用精密找平法进行竖向位移观测[14-15]。结合金盆水电站的实际情况，在大坝左岸选择二级找平测量路线，并设置一套三点找平基准点组。

4.1.1 水平位移

以布置监测仪器选取拱冠部分在高程433 m处坝顶测点LD1和LD2，高程400 m处坝底测点LD3和LD4水平位移为例，观测时段为2017年10月26日至2019年3月26日，各个时段相应的Comsol数值模拟和监测数据结果比较如图12所示。

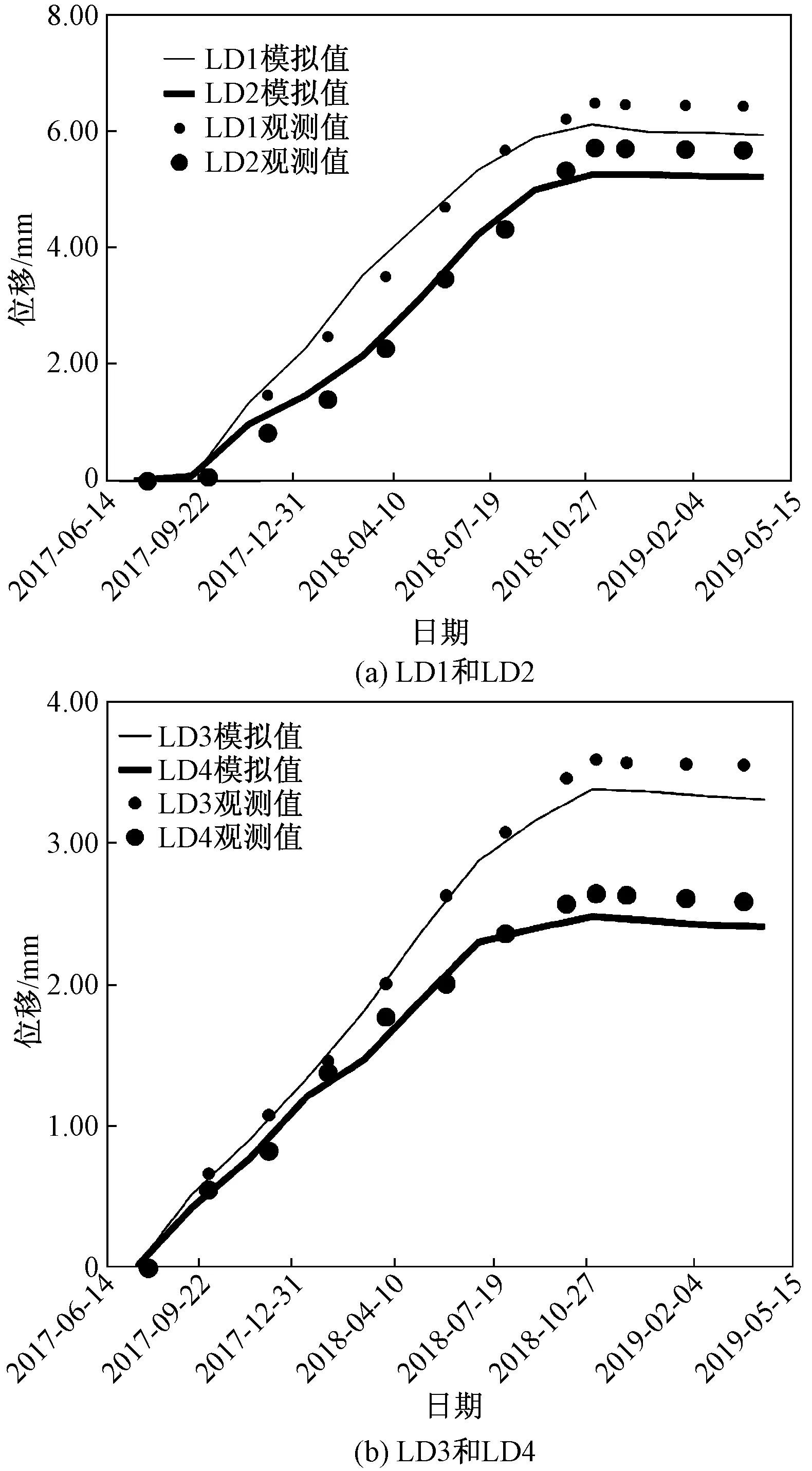
图12 各测点水平位移结果

由图12可知，监测和计算结果能较好吻合，坝顶测点LD1-LD2、坝底LD3-LD4二者的相对误差仅为(5.9%，8.0%)、(5.8%，6.0%)，验证了计算结果的正确性。坝顶测点(LD1-LD2)、坝底测点(LD3-LD4)主要表现为向上游位移，且位移随着大坝运行逐渐增大并趋于稳定，坝顶测点LD1-LD2、坝底测点LD3-LD4均在2018年10月达到最大值，分别是(6.48 mm，5.71 mm)、(3.59 mm，2.64 mm)随后趋于稳定，符合大坝变形的基本规律，变形满足要求。

4.1.2 垂直位移

以选取和监测水平位移时的同部位、高程、测点、观测时段下的垂直位移为例，各个时段相应的Comsol数值模拟和监测数据结果比较如图13所示。

图13 各测点垂直位移结果

据图13可得，监测和计算结果具有较好的一致性，坝顶测点LD1-LD2、坝底测点LD3-LD4二者的相对误差差值仅为(5.9%，5.8%)、(6.3%，5.8%)，更有效地验证了软件模拟值的正确率。拱坝垂直位移与时间具有较好的相关性，所有测点的数模位移值随大坝运行逐渐增大并趋于稳定，而观测位移值曲线随时间呈现弹簧变化，不同时段的波动随大坝的运行而逐渐变小并趋于稳定。

坝顶测点(LD1-LD2)、坝底测点(LD3-LD4)主要表现为向下游位移，均在2018年4月达到最大值，分别为(1.19 mm，1.39 mm)、(0.95 mm，0.70 mm)，随后趋于稳定，可见该坝在这种覆盖层坝基处理方式上沉降呈现变形协调状态，符合大坝变形的常规规律，变形在合理范围之内。

5 结论

借助Comsol Multiphysics建立模型以及监测资料对大坝位移进行分析和对比，论述了这种坝基处理方式的变形特点和安全状况，得到如下结论。

(1)多场耦合计算和实际监测结果能相互验证，说明了Comsol计算方法的准确性，应力和变形计算结果能反应大坝运行的实际情况。

(2)对比发现，坝体和坝基应力和变形均在规范要求范围内，满足强度和刚度要求，说明在不开挖覆盖层的情况下，采取三道防渗墙和高压旋喷桩的措施是合理的，可靠的。

(3)该坝基处理措施是首次应用于拱坝深基础处理之中，对于中小型深厚覆盖层上建造拱坝，采用本文方案不仅可以节省工期、造价等，而且能满足现行规范要求的各项指标，本研究可为同类型、类似地质条件下的拱坝设计提供参考。