锂离子电池的多状态模型剩余寿命预测方法
2021-05-14蔡艳平苏延召
陈 万, 蔡艳平, 苏延召, 姜 柯, 黄 华
(火箭军工程大学305教研室, 西安 710025)
锂离子电池在实际应用中的安全问题一直是人们关注的焦点[1-3],而预测与健康管理(prognostics and health management,PHM)技术能够有效监控锂离子电池的健康状态,提高电池工作时的安全性。其中准确的剩余使用寿命(remaining useful life,RUL)预测是实现PHM的基础,因此成为当前研究的热点。
基于经验模型的预测方法因为其预测结果较为准确,同时预测不需要专业的电化学基础,成为当前锂离子电池RUL预测常用的方法[4]。经验模型常采用的是指数经验模型[5],林娜等[6]、Zhang等[7]采用指数经验模型和改进的粒子滤波算法实现了锂离子电池RUL预测,然而该方法没有考虑容量再生现象的影响。锂离子电池的退化过程大都含有容量再生现象[8],容量再生现象表现为下一周期的容量高于上一周期,并且在容量再生后的一段时间出现加速退化,这严重影响RUL预测的精度。吴祎等[9]采用变模态分解的方法将退化过程分为了正常退化和容量再生过程,然后分别预测两种状态实现了RUL预测,然而该方法没有考虑容量再生现象的加速退化过程。曲杰等[10]采用小波降噪的方法对数据进行平滑处理,剔除了容量再生数据,然而该方法获得的退化曲线与实际的退化曲线存在较大差别。严仁远[11]通过分析电池在三种衰退模式下的衰退数据建立了多模式锂离子电池容量衰退模型并结合粒子滤波(particle filter,PF)算法实现了RUL预测,然而该模型的建模过程比较复杂。
基于上述问题,提出了一种锂离子电池的多状态模型剩余寿命预测方法。该方法提出的多状态容量衰退模型包含了锂离子电池的3种退化状态:正常退化、容量恢复、加速退化,因此模型更加符合实际的衰退曲线。该方法提出的粒子群优化粒子滤波(particle swarm optimization particle filter,PSO-PF)预测算法考虑了容量恢复数据相对不足的情况,避免了PF算法对学习数据的大量需求。
1 容量衰退模型建立
1.1 锂离子电池衰退数据分析
使用数据集来自美国国家航空航天局(National Aeronautics and Space Administration, NASA)公开的数据集,数据集中包含4块电池,如图1所示。从图1可以看出,锂离子电池的容量衰退存在容量恢复现象。图2为B0005电池的容量变化速率,可以看到B0005电池存在3种明显的衰退速率:一是衰退速率处于零以下,但接近零,这种状态占据整个衰退过程的大部分,是电池衰退的正常状态;二是衰退速率大于零,表现为下一周期测得的容量大于上一周期测得的容量,是电池的容量恢复现象;三是衰退速率远远超出正常衰退速率,该现象出现在容量恢复现象之后,是电池容量恢复后出现的容量加速衰退现象。基于此,将分别对三种衰退状态进行建模,然后将模型进行组合得到容量恢复效应下锂离子电池的容量衰退模型。模型的评价标准采用拟合优度R2和均方根误差(root mean squared error,RMSE)。
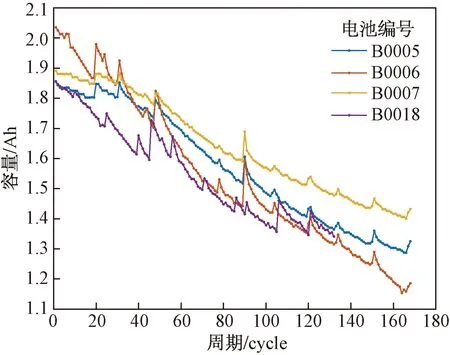
图1 衰退数据
1.2 正常衰退模型建立
分析可知,容量加速衰退现象只出现在容量恢复现象之后,同时考虑到测量过程中的测量误差,因此将NASA原始数据集中容量变化大于0.005 Ah的数据横向切割来获得正常衰退速率下的电池容量衰退数据,结果如图3所示。
观察图3可以看出,正常衰退速率下的衰退曲线具有良好的线性特征,因此采用一次线性模型进行拟合,同时使用目前常用的双指数经验模型进行拟合,结果如表1所示,一次线性模型和双指数经验模型都能较好地拟合正常衰退速率下的衰退数据,但在后续的预测过程中,经验模型需要处理4个参数,一次线性模型只需要处理两个参数,工作量可以大大减少,因此采用一次线性模型作为正常衰退速率下电池的衰退模型。模型中参数a、b的初始值采用模型拟合B0007电池的值。
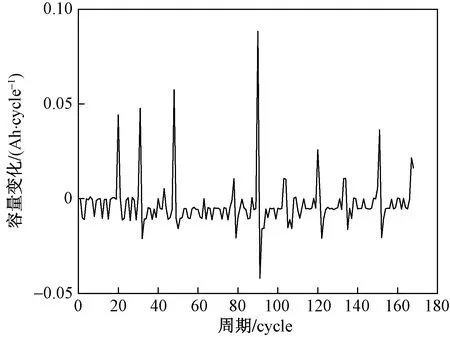
图2 B0005的容量变化速率
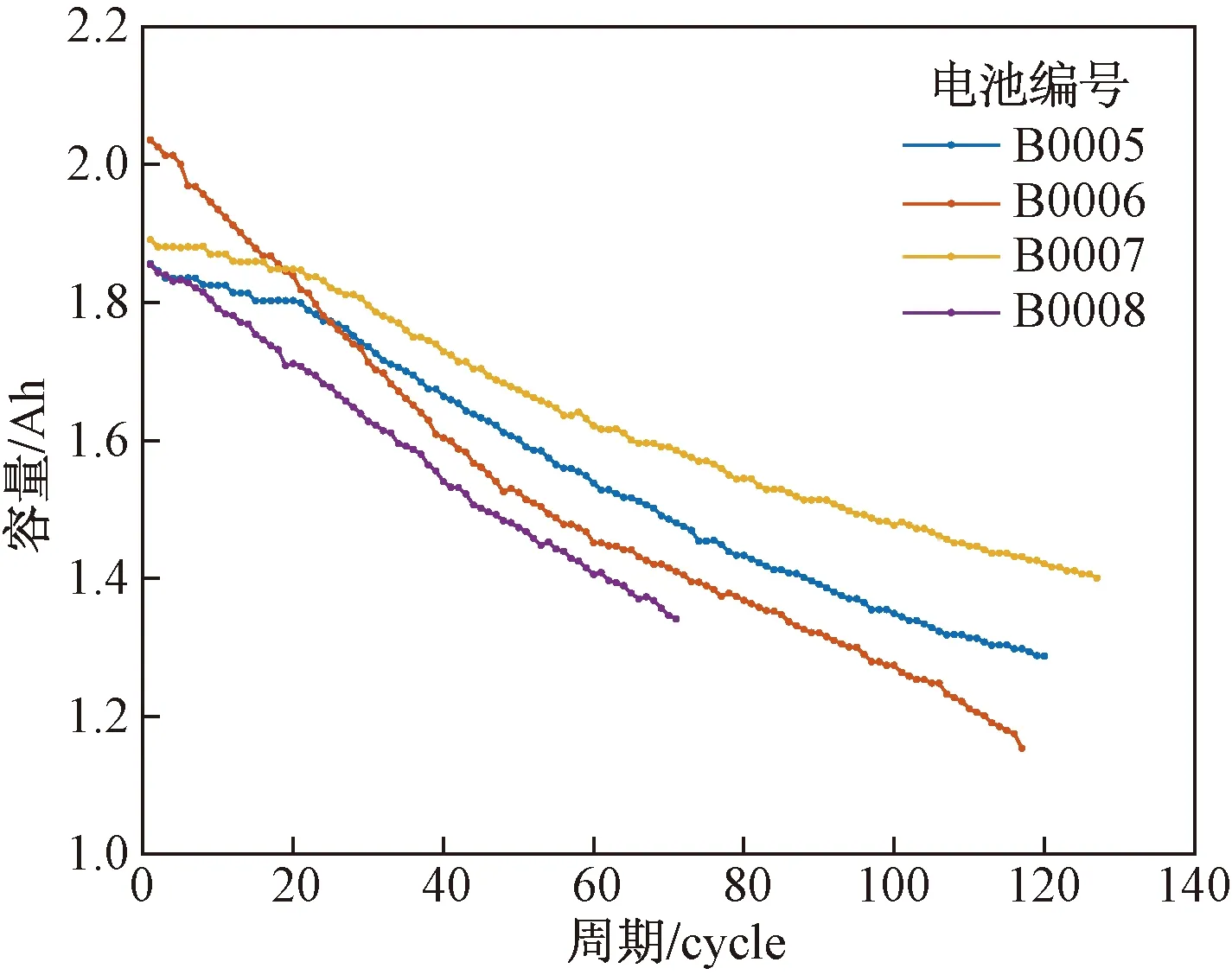
图3 正常状态的衰退曲线
1.3 容量恢复模型建立
Eddahech等[12]指出当电池搁置时间达到6 h以上,电池的容量就会出现较为明显的恢复,因此从四块电池中取出搁置时间超过6 h的数据点并剔除异常点,提取数据如图4所示。从提取数据可以看出,当搁置时间超过10 d后,恢复的容量出现了下降,这是由于电池本身还存在自放电、日历老化等现象。因此容量恢复模型需要满足以下两个条件:一是当搁置时间等于0时,其容量恢复的数值也为0;二是模型存在一个极大值点,即当搁置时间过长,会导致恢复的容量开始下降。受经验模型的启发,提出一个新的容量恢复模型[式(1)],其中c、d为模型变量,该模型能够满足上述两个条件。文献[11]通过分析B0005的容量恢复数据提出了容量恢复模型,如式(2)所示。
f(x)=cxexp(dx)
(1)
f(x)=cexp(-x)-c
(2)
式中:x为搁置的天数;f(x)为对应的容量恢复值。
使用上述两个模型对容量恢复数据进行拟合,其中B0005的拟合效果如图4所示,4块电池的拟合结果如表2所示。从表2可以看出,新模型的拟合效果是优于旧模型的,表明本文模型的精度更好;对于B0006和B0018电池,旧模型的拟合效果出现了明显的下降,而新模型对4块电池的数据拟合效果精度变化不明显,表明本文模型相对于旧模型具有更好的鲁棒性。
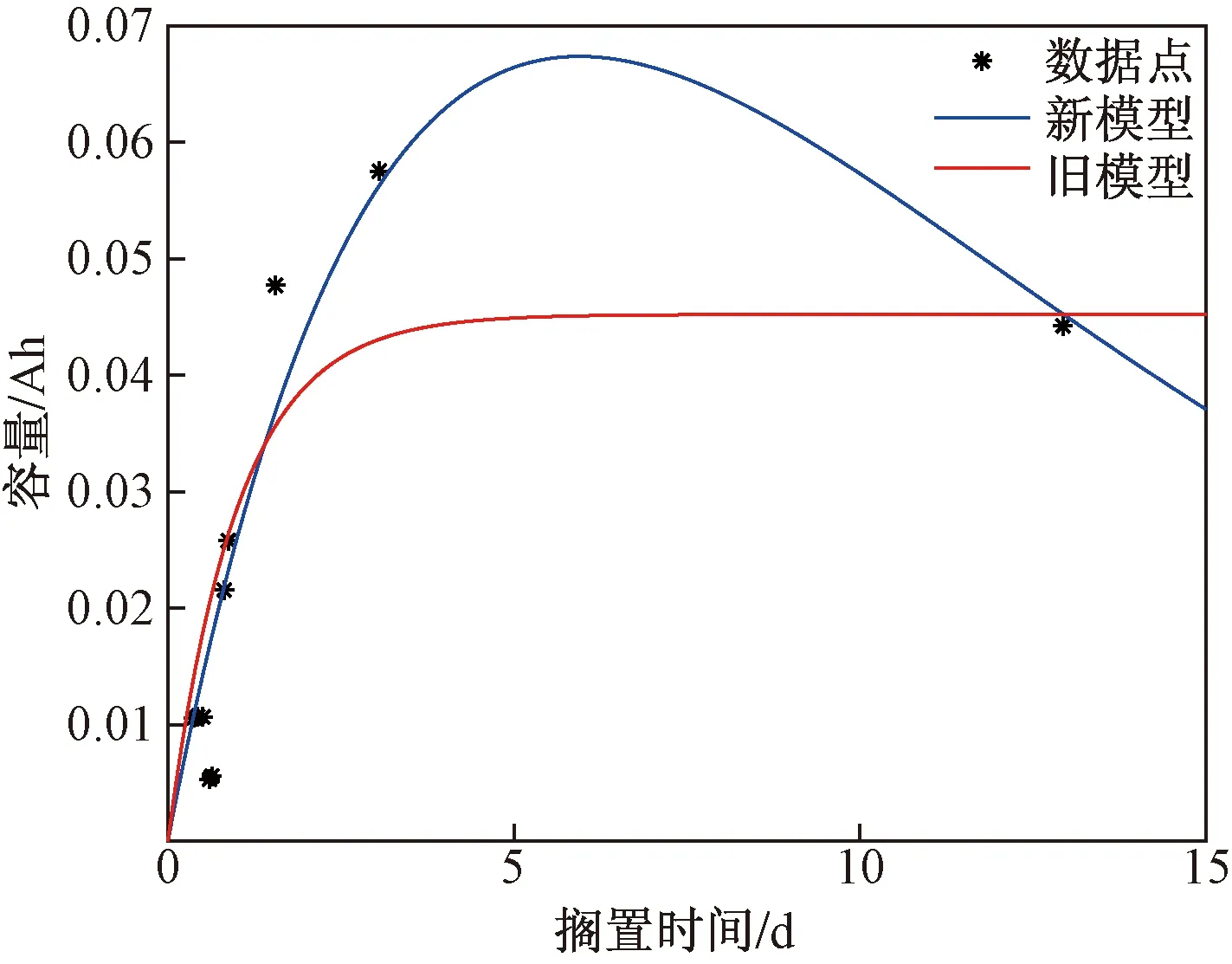
图4 容量恢复数据的拟合结果
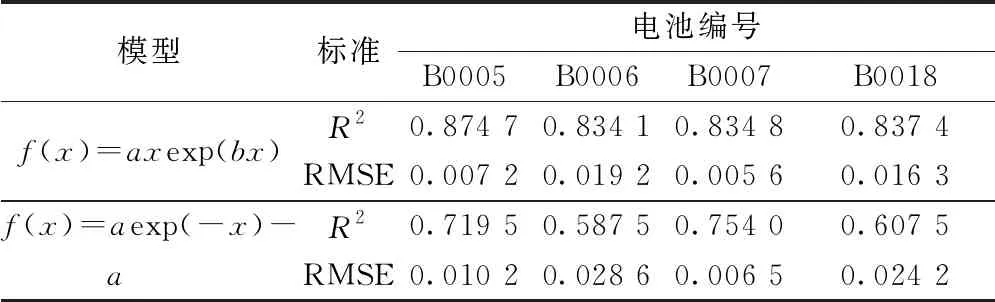
表2 拟合结果
1.4 加速衰退模型建立
容量加速衰退的持续时间相对于整个锂离子电池的衰退周期来说很短,因此为了不增加模型的复杂度,不考虑对加速衰退阶段进行单独的建模,而是在正常衰退模型中加入加速衰退因子,使其满足从恢复的容量衰退到恢复之前的容量所需周期与实际衰退需要的周期一致,因此加速衰退模型可表达为
f(x)=-(a+β)x+b
(3)
式(3)中:β为加速衰退因子。
从B0005中提取加速衰退阶段的数据,结果如表3所示。从表3可以看出,加速衰退速率不会随容量恢复的值的改变出现较大的波动,因此采用均值-0.010 498作为加速衰退速率的值。-a为B0005正常的衰退速率,从拟合结果可知,-a=-0.005 25,因此加速衰退因子为0.005 25。由于加速衰退阶段在整个阶段的比重很小,因此可以将该加速衰退因子作为所有电池在加速衰退阶段的加速衰退因子,从而减小模型的复杂程度。
1.5 多状态容量衰退模型建立
将三种状态下的模型组合得到最后的锂离子电池容量衰退模型为
(4)
f(t)=ctexp(dt)
(5)
Ccyc=f(t)/0.010 49
(6)
式中:Qk为第k个循环周期时电池的容量;kt为搁置时的电池周期;f(t)为容量恢复模型;t为搁置时间;Ccyc为加速退化过程经历的周期个数。
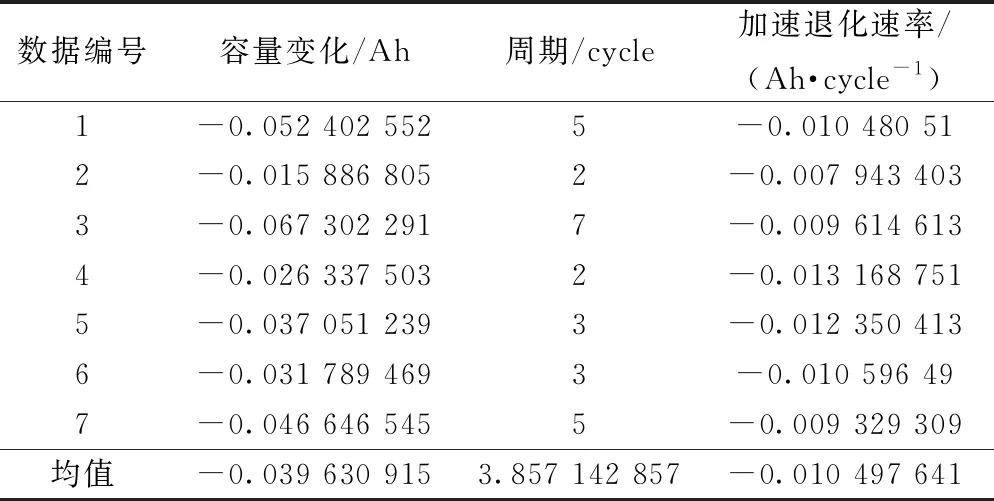
表3 B0005的加速衰退数据
2 多状态模型剩余寿命预测方法
2.1 基于PSO-PF的预测方法
基于经验模型的锂离子电池RUL预测中常用的预测算法是PF算法,但PF对样本的需求量较大。NASA锂离子电池容量衰退数据集在正常衰退速率下的衰退数据较充足,容量恢复数据较少,因此提出了PSO-PF算法来实现锂离子电池的RUL预测。其实现流程如图5所示。
PF算法是一种基于蒙特卡洛仿真的近似贝叶斯滤波算法,核心思想是用一些离散的采样点来近似随机系统的概率密度函数,以样本均值代替积分运算,从而获得状态的最小方差估计。PSO算法是一种基于群体协作的全局随机搜索优化算法,具有易于实现及计算量小等优点,常用于模型参数识别。PSO-PF算法首先使用PSO实现对容量恢复模型的参数识别,然后将参数识别后的锂离子电池容量衰退模型带入PF算法对正常衰退模型的参数进行更新,最后实现锂离子电池RUL预测。
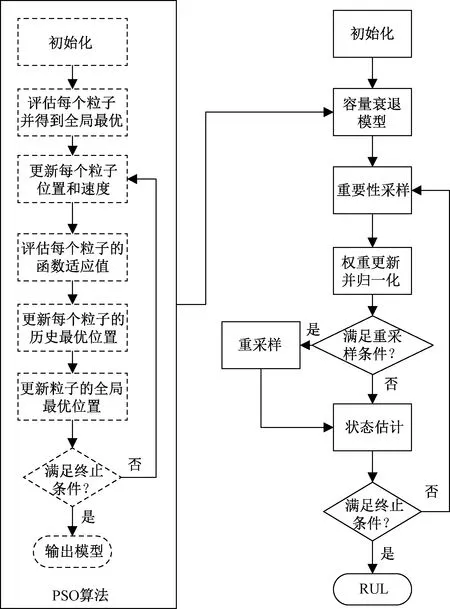
图5 算法流程
2.2 基于PSO-PF的锂离子电池RUL预测
基于建立模型得出系统的状态转移方程和测量方程为
ak=ak-1+wa,w∈(0,σa)
(7)
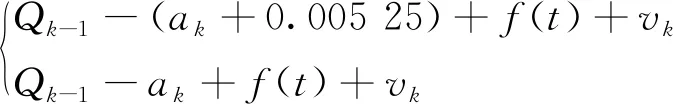
(8)
式中:ak表示第k个周期时参数a的值;wa为过程噪声;vk为测量噪声,vk∈(0,σv);σa、σv分别为系统噪声方差和测量噪声方差;Qk为k时刻测量的容量。
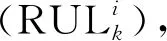
(9)
(10)
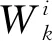
采用置信度为90%的置信区间表达预测结果的不确定性,实现步骤如下。
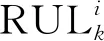
Step 2计算置信区间上下限。
id=round(0.05N)
(11)
iu=round(0.95N)
(12)
式中:id、iu表示上、下限;round(·)表示取整函数;N表示粒子数。
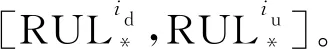
预测结果采用两种标准进行评价:绝对误差(absolute error,AE)和均方根误差(root mean square error,RMSE)。
3 实验结果对比分析
设置粒子数N=1 000,搁置时间序列从B0007获得。对B0005,在预测起点T=60采用双指数经验模型加PF的预测方法实现RUL预测,多状态模型加PSO-PF算法实现RUL预测及预测结果的不确定性表达,将预测起点改为T=90,重复上述的实验。对B0006,在预测起点T=60和T=95,采用与上文相同的方法实现RUL预测。最终预测结果如表4所示,同时两块电池在T=60时的预测曲线和本文方法预测结果分布如图6、图7所示。
从图6(a)、图7(a)可以看出,采用本文方法进行RUL预测获得的预测曲线比采用经验模型+PF预测方法更加贴合实际的衰退曲线。从图6(b)、图7(b)可以看出,预测结果的分布为正态分布,符合实际情况,图6(b)存在分布间断现象是由于B0005在寿命阈值附近存在搁置导致的容量恢复,而容量恢复会增加电池的RUL。从表4可以看出,对同一个电池在相同或不同的预测起点下,采用本文方法进行RUL预测获得的预测结果的绝对误差、置信区间和均方根误差更小,表明本文方法的准确性更好。同时当预测起点增大时,预测结果的相对误差减小,这符合实际情况。对于不同的电池,本文方法也获得了更好的精度,表明本文方法鲁棒性较好。
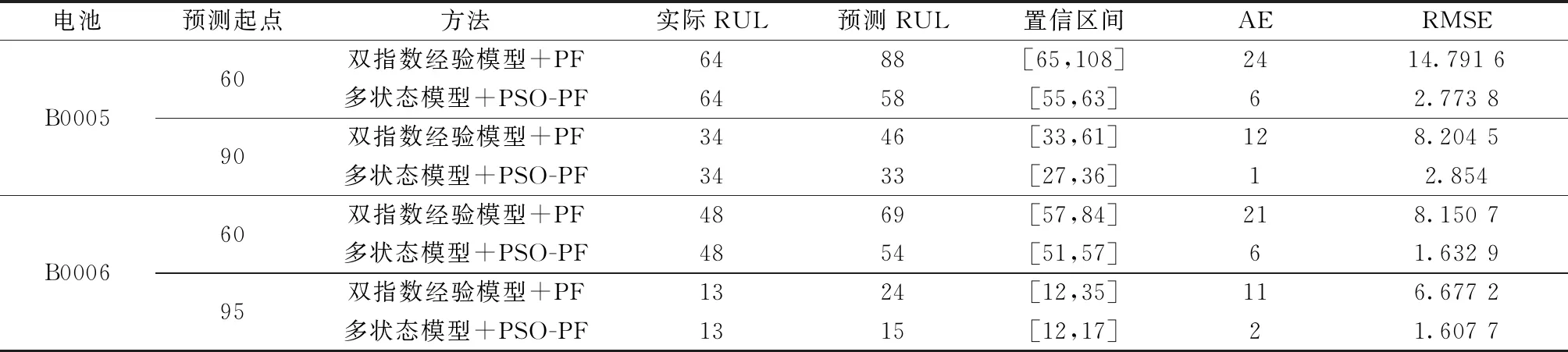
表4 预测结果
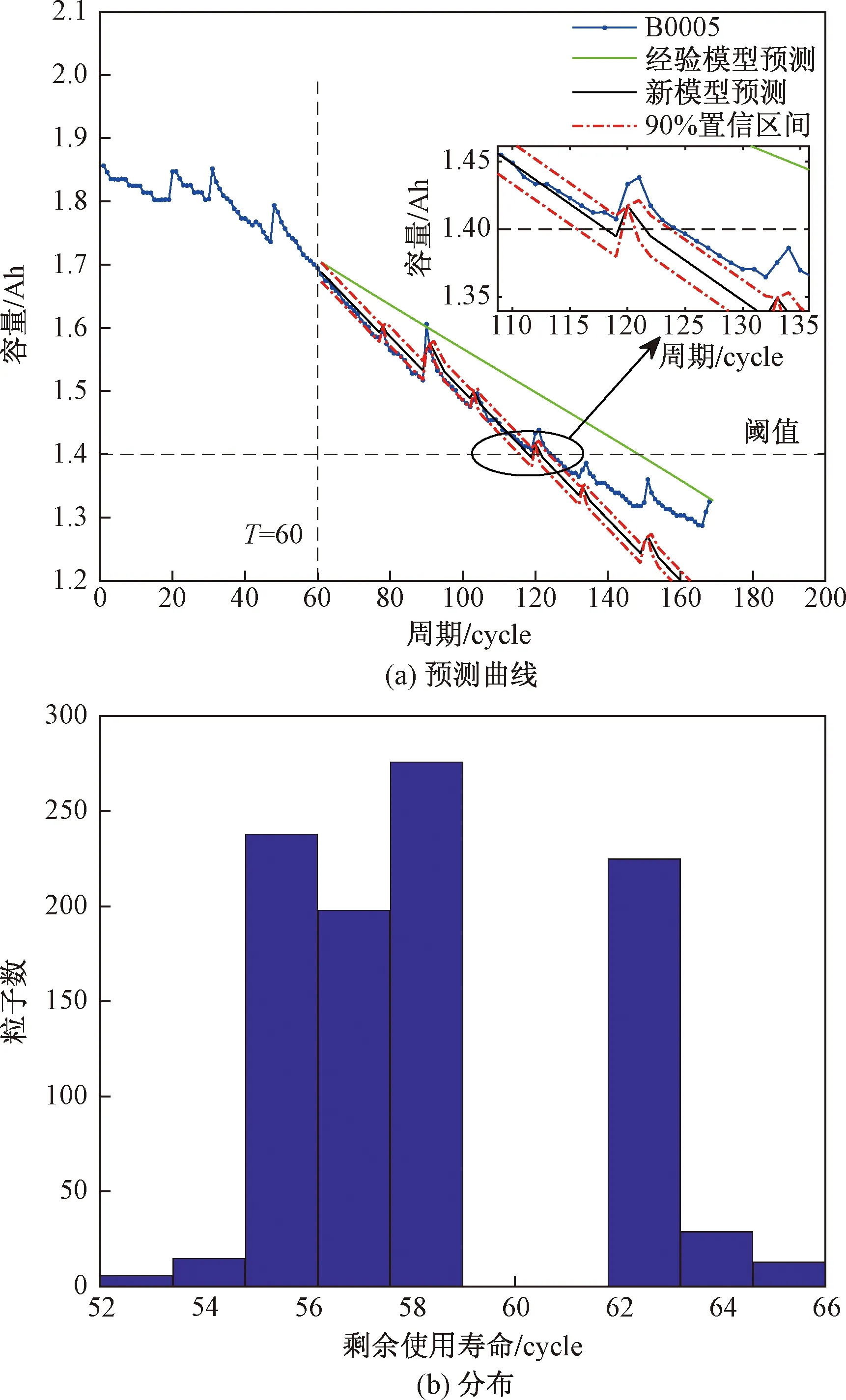
图6 B0005预测结果
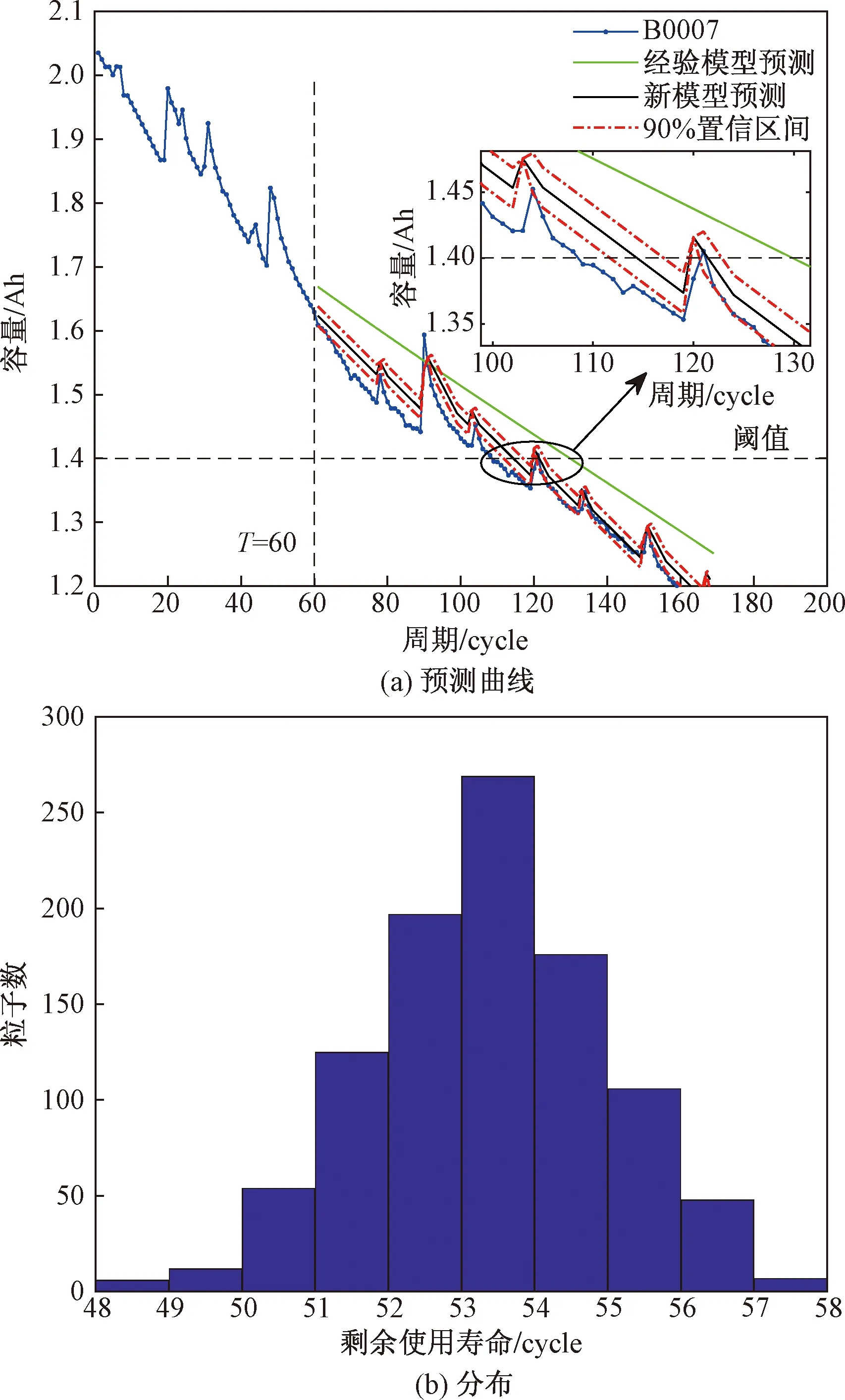
图7 B0006预测结果
5 结论
(1)针对锂离子电池存在的容量恢复现象,提出了考虑容量恢复效应的锂离子电池多状态容量衰退模型,结果表明,本文模型与双指数经验模型和多模式模型相比,模型拟合效果更好。
(2)针对提出的模型,提出了PSO-PF预测算法,实现了锂离子电池RUL预测并给出了预测结果不确定性表达方式,结果表明,本文算法能够在容量恢复数据较少的条件下达到较好的预测效果。
(3)对比分析了本文方法与基于双指数经验模型的预测方法的预测结果,结果表明本文方法具有较高的精度;对比分析了本文方法在不同电池的预测结果,结果表明本文方法具有较好的鲁棒性。
