基于熵权-离差的GA-BP神经网络编程能力评估方法

罗文劼， 李明杰， 肖梓良

(河北大学网络空间安全与计算机学院，保定 071002)

教育数据挖掘(educational data mining，EDM)是运用教育学、计算机科学、心理学和统计学等多个学科理论和技术来解决教育研究与教学实践中问题的一种方法[1]。随着在线学习平台的不断发展，EDM已成为当前解决教育数据研究的热点。EDM对教育相关数据进行分析与研究，主要应用有发现学习规律、分析学习特征及习惯、评估学习现状、可视化、学习者建模、学习者表现预测、推荐系统和自适应系统等[1-2]。将教育系统积累的大量学习数据通过数据挖掘技术得到的客观信息反馈，有利于学习者掌握自己的学习情况，同时，有助于教育者的教学管理。

在线评测系统(online judge，OJ)是对用户提交的算法源代码进行评测而设计的在线自动判题系统[3]。随着ACM(国际计算机协会)国际大学程序设计竞赛(ACM/ICPC)等程序设计竞赛的普及，OJ系统也得到了快速的发展，为编程实战提供了一种新的方式[4]。近些年来，中外很多高校拥有自己的OJ系统，如北京大学的POJ、浙江大学的ZOJ、古巴信息科学大学的COJ和俄国萨拉托夫国立大学的CodeForce等，OJ作为学习者编程训练的平台，对提高学习者的编程能力具有很重要的作用。

目前，中外已经有部分研究者使用数据挖掘技术对学习者的编程数据进行挖掘，从而预测学习者的成绩和评估其编程能力水平。在国外的研究中，Watson等[5]基于分析编程学习过程中直接记录的数据，介绍了一种Watwin的动态加权算法，通过对不同的特征进行加权来预测程序设计中的学生的成绩；Sagar等[6]提出监督学习的方法来预测学习者的编程能力，揭示学习者编程学习的潜在趋势，不仅可以帮助学习者实现自我认识，还可以帮助教育工作者评估学习者的学习进度；Carter等[7]通过学习分析编程状态，根据编程过程中的编译、调试以及编码过程和测试特征构建统计模型，发现不同编程能力水平的学习者之间差异。在中国的研究中，石振强[8]分析了在线评测系统与学习者之间的交互方式，采用k-means聚类算法分析学习者的行为，建立学习者成绩预测模型；张永梅等[9]采用模糊神经网络设计实现程序设计能力的评价方法，王明艳[10]建立基于反向传播(back propagation, BP)神经网络的大学生编程能力动态评估模型，用模糊层次分析法确定各评估指标的权重，但是此方法具有主观性和单一性，而且模糊逻辑与BP神经网络的结合并没有解决BP神经网络求指标权重时容易陷入局部极小化的问题。

通过分析以上中外有关编程能力研究成果，针对OJ系统上缺乏对学习者编程能力的客观反馈和只凭借最终成绩评价学习者的方法单一化的问题，提出基于熵权法和离差最大化方法的遗传算法优化BP(genetic algorithm-back propagation, GA-BP)神经网络的编程能力评估方法，以 EDM 为基础，采集并分析该系统上记录学习者的历史学习数据，提取学习者完成编程题目的正确数量、重复提交次数、程序评测结果[11]、程序调试时间[12]和成绩5个指标来反映一个学习者的编程能力水平，用双参数平衡熵权法和离差最大化的客观组合赋权方法克服文献[9-10]在评估学习者编程能力利用模糊层次分析法确定指标权重的主观性和赋权方法单一化的问题，同时，利用GA随机搜索最优解的优势来避免BP神经网络确定指标权重易陷入局部极小化的问题，构建GA-BP神经网络评估模型，实现对学习者编程能力的客观评估。

1 编程能力评估指标体系

1.1 概念的符号定义

(1)将学习者定义为u，编程题目定义为p。学习者集合为U={u1,u2,…,um}，编程题目集合为P={p1,p2,…,pn}，其中，m表示学习者的数量，n表示编程题目的数量。

(2)将学习者学习信息定义为S。设学习者u在题目p上的学习记录由Sp(u)=[Su,p,0,Su,p,1,…,Su,p,l-1]T∈Rl表示，其中，所有学习者的学习信息都被存储在SU×P×l中，可通过提取S中的特征形成评估学习者编程能力的指标体系I，I={X1,X2,…,Xq}，其中q为评估指标的个数。

(3)将学习者编程能力定义为B。设B={value}U×P表示所有学习者的编程能力评估值。其中，value描述通过计算S中所记录学习者u在不同编程题目p上的各指标数据所得的综合评估值。

1.2 评估指标的描述

OJ系统编程实战数据量大，每个学习者在线编程学习的记录S都形成记录其隐性学习效果的载体，对学习者的历史学习信息进行系统分析，并参考文献[8，11-12]有关在线评测系统编程数据的研究，提取编程能力评估指标，首先对各指标进行描述，具体如下：

(1)调试题目时间Tdebug。将学习者u提交编程题目p的开始时间定义为Tstart，将最后一次修改结束后提交时间定义为Tend。

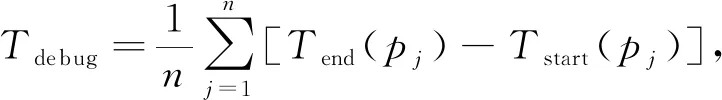
(1)

j=1,2,…,n

(2)正确提交数NAC。OJ的基本测试结果包括编译错误(CE)[11]、运行错误(RTE)[11]、答案错误(WA)[11]、系统错误(SE)[11]、运行超时(TLE)[11]、运行超内存(MLE)[11]和评测成功(AC)[11]7种，评测结果result={CE,RTE,WA,SE,TLE,MLE,AC}，设

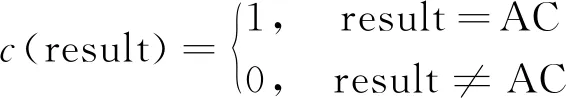
(2)

每个学习者的正确提交数NAC为

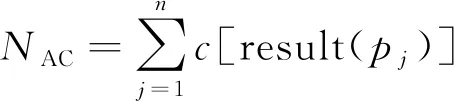
(3)

(3)错误类型数Nf-type。当η⊆result且AC⊄η时，

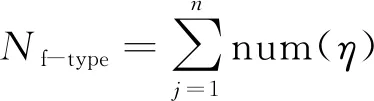
(4)

式(4)中: num(η)为η中元素的个数。

(4)重复提交次数rsubmit。设λ表示完成题目所提交的次数，则

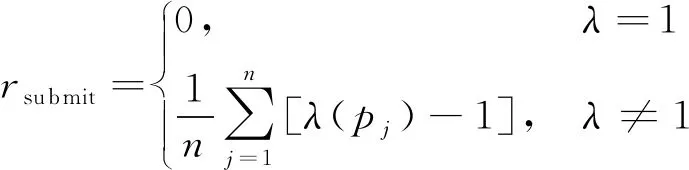
(5)

(5)总成绩Ts。设s表示学习者u完成题目pj的成绩，则Ts为

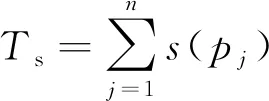
(6)

由以上各指标组成的评估学习者编程能力指标体系I={X1,X2,X3,X4,X5}，然而各指标权重未知，需确定每个评估指标的权重。确定指标权重的方法有主观赋权法、客观赋权法和组合赋权法。主观赋权法有Delphi法和层次分析法等，但是其具有主观性，易受到人的知识结构和经验能力的影响。客观赋权法是对信息进行客观的处理，主要有主成分分析法和熵权法等，但其计算结果难以解释，而且单一的赋权法又具有一定的片面性。因此，提出熵权法和离差最大化的客观组合赋权法，熵权法强调信息数据本身的重要程度，忽视了数据之间的联系，而离差最大化方法只注重信息数据之间的关系，恰恰能够弥补单一熵权法的这一不足，综合考虑信息本身和信息之间的关系来确定各指标的权重，并引入双参数来平衡二者之间的关系。

BP神经网络具有自学能力、客观性、非线性映射和求解率高的优点[13]，在综合评价领域得到了广泛的应用。但是BP神经网络求权重容易形成局部极小化，GA具有全局搜索能力，能够解决这一问题。所以，构建基于熵权法和离差最大化方法的GA-BP神经网络编程能力评估模型，流程如图1所示。

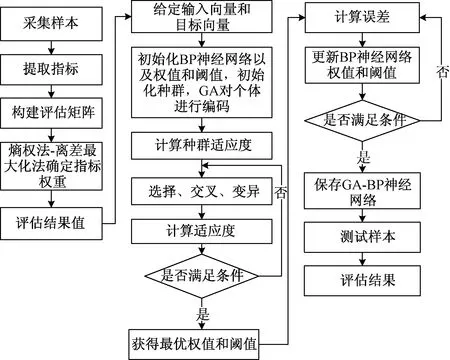
图1 熵权-离差的GA-BP神经网络流程

2 熵权-离差的GA-BP神经网络评估模型

2.1 熵权法-离差最大化原理

熵权法(entropy weight method, EWM)是利用熵值来评估各指标的变异程度、确定指标的权重和度量数据所提供信息量大小的方法[14]。熵值越小，其所包含的不确定性越小，说明指标传递的有效信息量大，指标所占的权重越大，该指标在评估中的影响就越大；反之，指标的熵值越大，其所包含的不确定性越大，则该指标在评估中产生的影响就越小。

离差最大化方法(maximizing deviation method, MDM)是利用评估指标值的离散程度大小确定相应指标的权重[15]。对于指标的值之间若是有较大的差异，则说明该指标对最终的评估结果影响大，应该赋予该指标较大的权重；反之，对于指标的值之间若是有较小的差异，则赋予该指标较小的权重。

由于每个指标存在不同的量纲，在对评估指标的权重进行计算时，量纲的存在会影响各指标之间的比较，也不利于模型构建。所以，需要对指标进行无量纲的标准化处理，实现数据的大小能够很直观地表现被评估对象的优劣情况。评估的指标分为效益型指标和成本型指标，对应效益型指标的值越大越好，成本型指标的值则越小越好。

设原始评估矩阵R=(xij)m×q，对R标准化处理后得到矩阵R′=(bij)m×q。

对于效益型指标而言，有

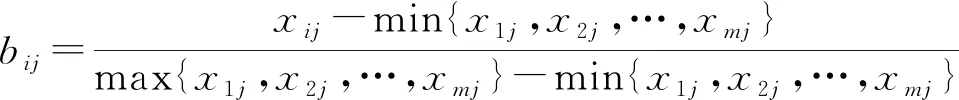
(7)

对于成本性指标而言，有

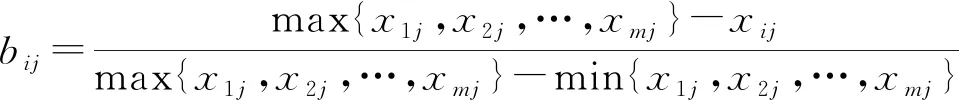
(8)

式中:xij为第i个评估对象的第j个指标的值；bij表示归一化后无量纲的标准数据。

熵权法-离差最大法求各指标的权重以及确定评估结果的过程如下。

2.1.1 构建评估矩阵

设有m个评估对象，q个评估指标，评估指标的综合权重为w′=(w′1,w′2,…,w′q)。

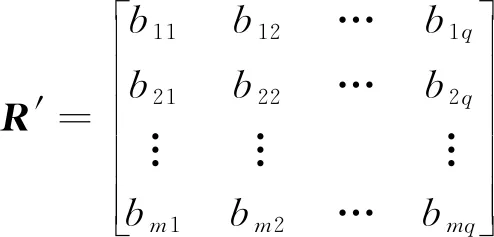
(9)

2.1.2 熵权法确定各指标的权重

(1)对于各指标仅考虑信息本身的重要性，即从熵权法角度出发，根据熵的定义，确定各评估指标的熵值。

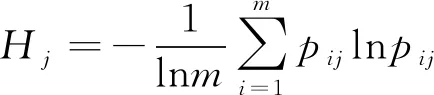
(10)

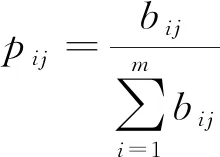
(11)

式中:j=1,2,…,q；0≤Hj≤1。

(2)指标Ij的信息熵为Hj，熵权法求得各指标权重为wj，具体计算公式为

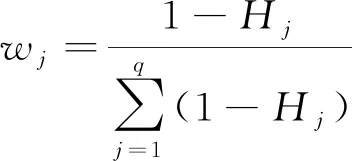
(12)

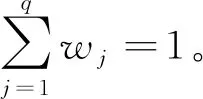
2.1.3 离差最大化法求各指标权重

离差最大化方法只注重信息间的关系而忽略信息本身的关系。在满足归一化和权重约束原则的条件下，计算其权重，目标函数计算如(13)所示。

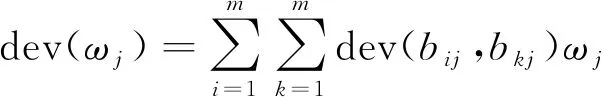
(13)

式(13)中：dev(bij,bkj)表示对于bj指标，评估对象bi和其他评估对象的离差；bij、bkj分别为第i个和第k个评估对象的第j个指标值；ωj为第j个评估指标的权重。

指标权重的选择根据所有的评估对象的所有评估指标的总离差最大化的原则，建立如下线性规划模型T：

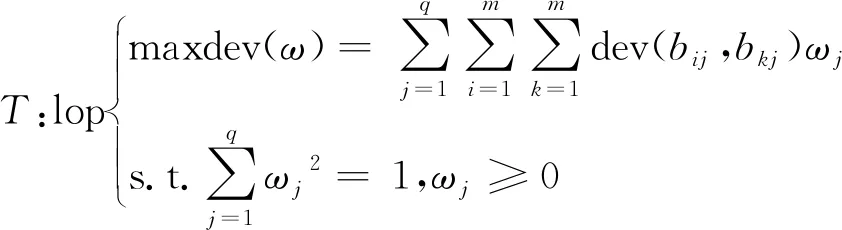
(14)

利用拉格朗日函数求解T:

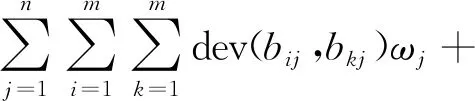
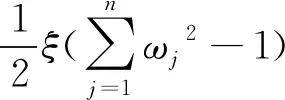
(15)

分别对ωj和ξ求偏导，最后得到模型最优解ω*。

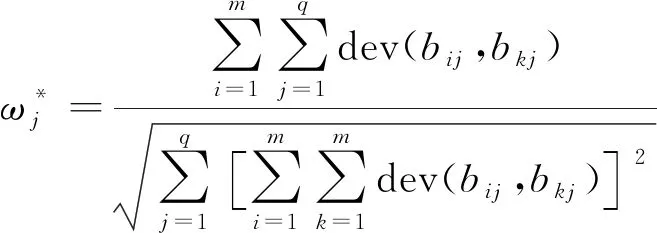
(16)

归一化处理后得ωj，即

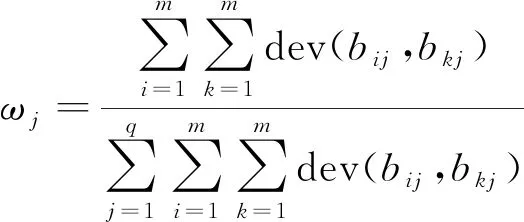
(17)

2.1.4 综合熵权法求得的指标权重w和离差最大化求得的指标权重ω，引入双参数确定指标的综合权重

首先，以欧氏距离确定二者间的距离，即

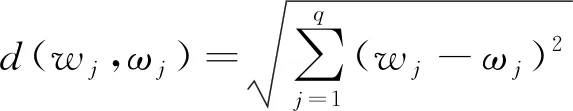
(18)

用双参数表示修正后的实际权重w′,即

w′j=αwj+βωj

(19)

式(19)中:α和β分别表示熵权法和离差最大化方法权重偏好系数，且满足以下约束条件：

d2(wj,ωj)=(α-β)2

(20)

α+β=1

(21)

式中:α≥0；β≥0。

2.1.5 确定综合评估结果

学习者样本的综合评估值B为w′与R′的合成运算,即

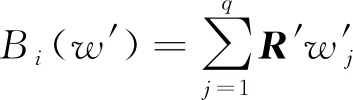
(22)

2.2 GA-BP神经网络

BP神经网络是广泛应用的神经网络模型之一，该网络的结构具有输入层、隐藏层和输出层。BP神经网络的学习过程由正向传播通过输入层神经元把输入网络的信息经过隐藏层的计算传向输出层，而且每一层的神经元只对下一层的神经元的输出状态有影响[13]，若实际输出值与期望值不符，则进行反向传播，计算输出误差，将误差信号从输出层再传向输入层，此过程不断修改连接每层神经元的权值和阈值，直至结果能够实现网络的预期效果，其结构如图2所示。图2中，X表示评估指标，Y表示输出层神经元的输出值，wij和wjk分别为连接输入层到隐含层与隐含层到输出层之间的权值。

BP算法虽然能够拟合非线性关系和提高复杂问题求解精度，且对数据资料没有严格的要求，但是网络易陷入局部极小化，随机赋予的权值和阈值也会使得网络的收敛速度减慢。BP神经网络存在的这些不足会对其应用造成一定的影响。

GA是一种全局优化随机搜索算法，通过遗传算子来模拟生物遗传过程中的选择、交叉和变异过程，从而获得最优个体[13]。GA计算过程简单，而且不依赖于问题本身，利用GA优化BP初始网络的权值和阈值，收敛速度快，增强评估模型的准确性。

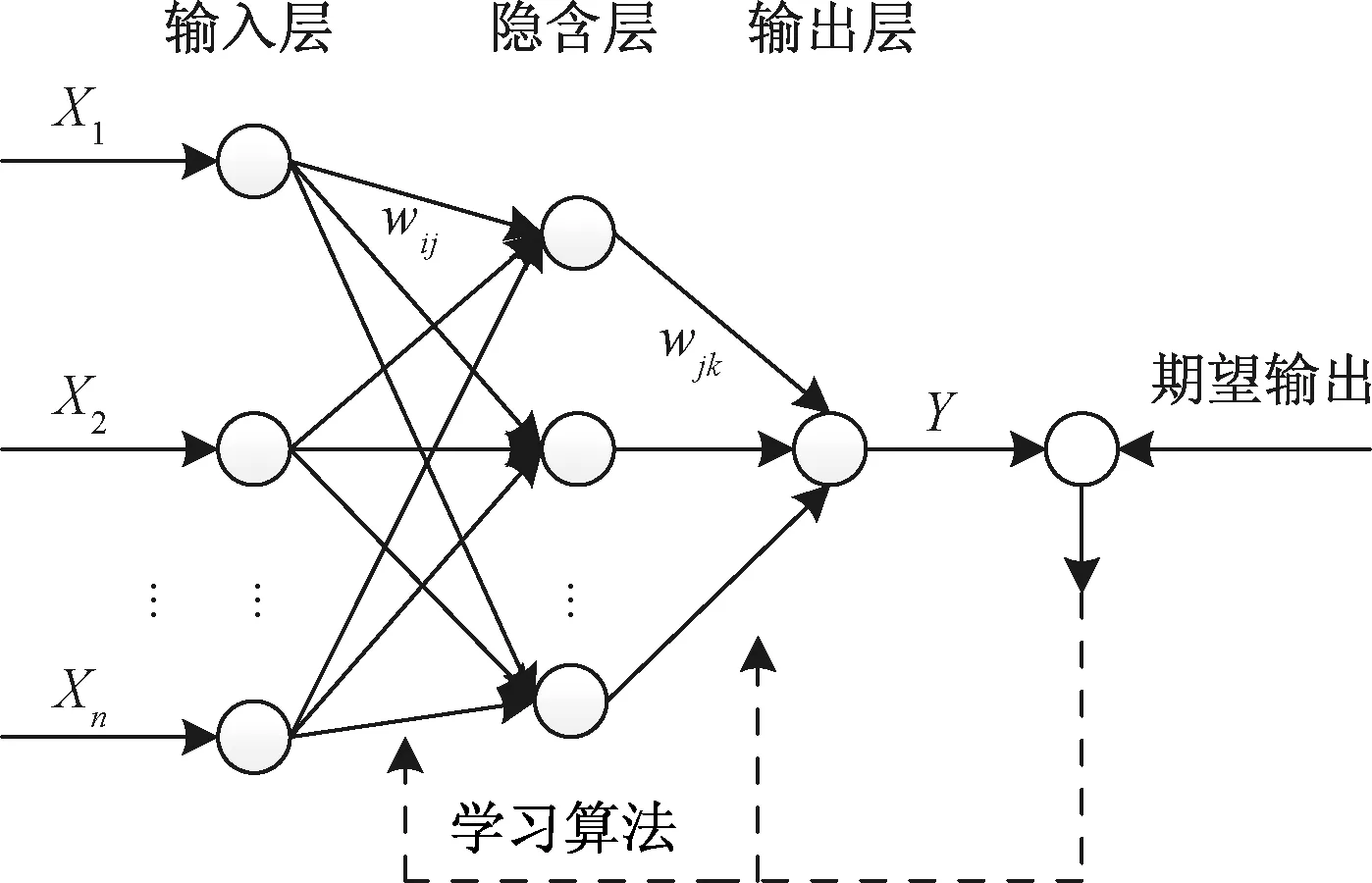
图2 BP神经网络结构

3 实验设计与结果分析

3.1 数据来源

OJ现用于编程能力训练、程序设计类课程的在线考核与测验，为了保证数据的真实性和评估的客观性，采用程序设计类实验辅助教学平台上120名学习者的编程实战测验数据为验证实例，通过采集学习者提交编程题目的数据和评测信息，参照编程能力评估指标体系，对各指标值进行提取并进行数据预处理得到归一化数据，并将前80名学习者样本数据用于GA-BP神经网络的训练，其余样本用于测试网络的性能，利用GA-BP神经网络模型得到各学习者编程能力评估值，并设计相应的能力评估等级，如表1所示。

表1 编程能力评估等级

3.2 构建GA-BP神经网络模型

3.3 评估结果分析

通过熵权法和离差最大化法计算得出各评估指标的具体客观权重，熵权法对应指标X1、X2、X3、X4和X5的权重分别为0.161 5、0.208 3、0.362 0、0.079 5和0.188 7，离差最大化法对应各指标权重分别为0.215 5、0.198 8、0.187 3、0.201 5和0.196 9，结合式(20)计算两种方法综合指标权重w′为0.182 6、0.204 6、0.293 9、0.127 1、0.191 9。在此基础上，通过式(22)得到各学习者编程能力评估值，将评估值作为GA-BP神经网络的期望输出，用GA-BP神经网络模型进行训练，得到最接近期望输出的评估模型，保存GA-BP神经网络进行测试，将期望值与实际输出值进行对比并计算二者之间的绝对误差。测试结果和评估等级如表2所示。

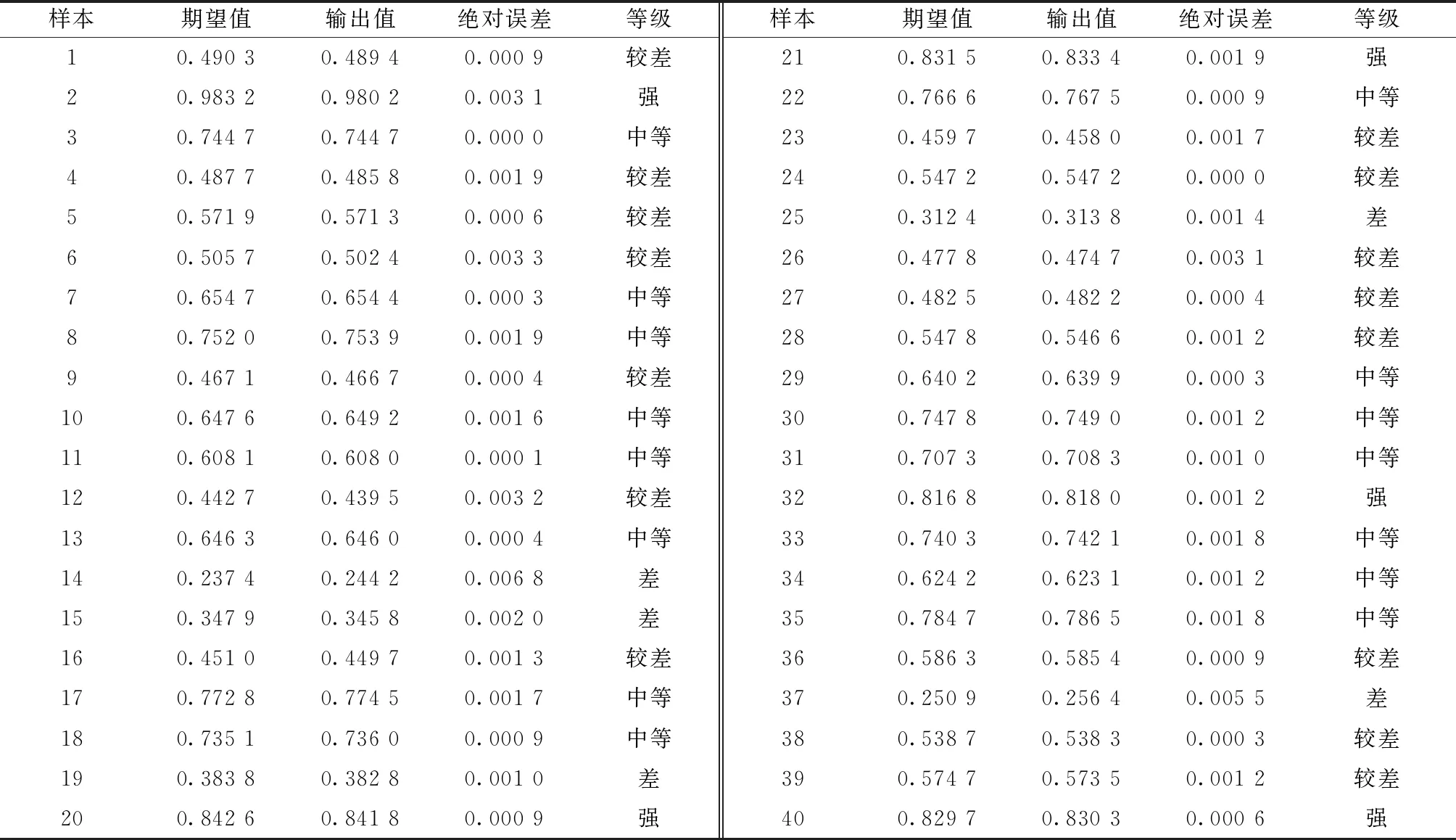
表2 GA-BP神经网络测试结果与误差

由表2可知，GA-BP神经网络的实际输出和期望输出值之间的最大绝对误差值为0.006 8，最小值为0，误差值很接近。因此，基于熵权和离差的GA-BP神经网络模型能够实现对学习者编程能力的评估。

3.4 模型评估性能对比分析

建立基于熵权和离差的GA-BP神经网络训练模型以及数据归一化处理均采用MATLAB语言实现，并将该模型与单一BP神经网络评估模型的实验进行对比，用平均相对误差(mean relative error,MRE)来评价模型的有效性。MRE的定义为

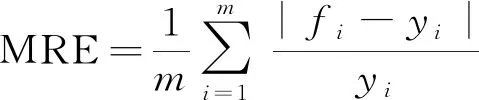
(23)

式(23)中:yi为期望输出值；fi为实际输出值。

通过实验测试，基于熵权和离差的GA-BP神经网络模型的MRE为0.34，单一BP神经网络的MRE为0.69，GA-BP 神经网络和单一BP 神经网络的相对误差曲线对比如图3所示。

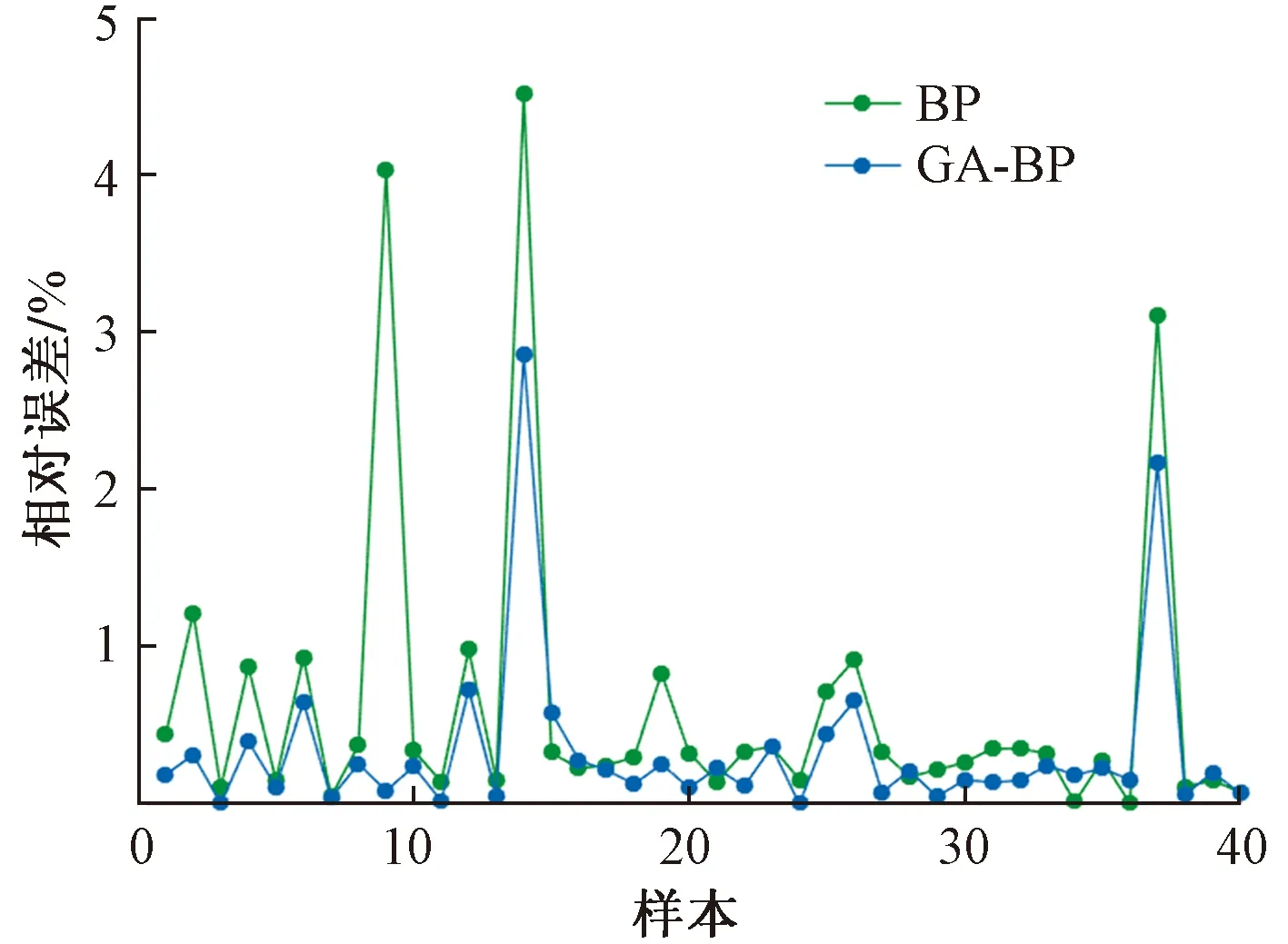
图3 GA-BP与BP神经网络相对误差比较

由图3可知，基于熵权和离差的GA-BP神经网络的误差小，评估结果更准确。

4 结论

(1)构建基于熵权和离差的GA-BP神经网络编程能力评估模型，提取编程能力评估指标，采用熵权法和离差最大化法的客观组合赋权法，减少了主观因素的影响；同时，引入双参数修正二者的权重以确定各指标的综合权重，从而计算期望输出，将其作为GA-BP神经网络的期望输出，优化了BP神经网络求权重带来的误差。

(2) GA优化BP神经网络的初始值和阈值，克服BP神经网络求权重易陷入局部极小化的缺点，使得网络的收敛速度加快，增强BP神经网络的鲁棒性，而且，与单一BP神经网络的评估结果相比较，GA-BP神经网络的评估误差小。

(3)用熵权和离差的GA-BP神经网络模型建立OJ上学习者编程能力评估模型，输出值和期望值的误差较小，可以实现对学习者编程能力的评估且评估结果更准确，能够帮助学习者掌握自身编程能力水平；同时，为辅助高校教育教学管理和企业招聘优质人才提供参考。在今后的工作中将会考虑更多维度的信息在编程能力建模中的应用，并利用编程能力研究结果更准确地进行个性化推荐的研究。