基于变权马尔可夫随机场的遥感图像变化检测

高 鹏 翔

(中国工程物理研究院计算机应用研究所 四川 绵阳 621900)

0 引 言

随着人类科技水平的迅猛发展，人类在地球上的活动范围愈发广泛。因此及时、精确地开展对地观测来实时监测地表的覆盖变化情况，对人类的发展具有重要意义[1]。当代航空、航天和传感器等技术的进步，促使了遥感图像获取手段的日益成熟[2]。当下采用遥感数据进行变化检测已是监测地表覆盖变化最精确、高效的技术手段，亦是遥感研究的热点。遥感图像变化检测是指通过分析一对或者一系列在相同地区不同时间点获取的遥感图像，来确定地表是否发生改变的技术[3]。

变化检测已在城市规划与建设农业、牧业、林业、工业、军事等领域内得到了普遍地运用，如土地利用/土地覆盖情况监测、地理数据库更新、灾害评估、森林植被覆盖监测、土地沙漠化监测、水系变化监测、城市建设规划、军事目标监测等[4-8]。

马尔可夫随机场模型(MRF)由于其完备的数学理论，以及能够充分利用图像中的空间上下文信息[9]，在遥感图像变化检测上取得了可喜的成就。Bruzzone等[10]首先使用MRF进行遥感图像变化检测，对差值图像使用EM算法，分别估计不变类和变化类概率密度，之后引入MRF，通过条件迭代式(ICM)算法[11]求解。Benedek等[12]采用条件混合马尔可夫模型来进行变化检测，这是一种多层MRF模型，结合了混合马尔可夫模型和信号的条件独立随机场。Chen等[13]提出了一种上下文敏感的弱监督变化检测技术，该方法通过MRF模型分析概率高斯过程分类器的后验概率实现。Chen等[14]针对传统的MRF方法在不连续区域(如边界、山脊、山谷等)经常得到错误的变化检测结果，提出了一种无监督变化检测算法。Gong等[9]提出了一种基于模糊聚类和改进MRF能量函数的SAR变化检测算法，该方法在计算能量函数时同时考虑了像素点的隶属度和同种类别的邻域像素数目改变。Subudhi等[15]提出了一种基于模糊聚类和MRF的变化检测算法，使用模糊吉布斯马尔可夫随机场(GMRF)来对差值图像的空间灰度特性建模，采用基于可变邻域搜索的全局收敛准则来迭代估计模糊GMRF模型的参数，避免了传统算法容易得到局部最优值问题。范奎奎等[16]将双树复小波变换和MRF相结合，解决了变化检测中多尺度图像降噪时丢失高频信息与单像素孤立问题。

然而，传统的基于马尔可夫随机场的变化检测算法，对于中心像素和邻域像素使用固定的权重，会造成空间邻域信息的过度使用[14-15]，使得传统的标记场不能精确地确定邻域像素间的空间关系，导致变化检测结果过度平滑，影响变化检测的精度。

针对上述问题，本文提出一种基于变权马尔可夫随机场的遥感图像变化检测算法。首先通过两时图像生成差值图像；随后使用模糊C均值聚类算法对差值图像上的像素点进行分类；接着使用一个改进的MRF模型来对差值图像建模；最后使用ICM算法求解能量函数最小化得到变化检测结果。

1 传统的基于MRF的变化检测

定义大小为M×N的两时差值图像为XD，其满足XD={x1,x2，…，xn}，n=M×N。变化类别与未变化类别为ω={ωch,ωun}，Y为类别标记场，对于二值变化检测问题，将图像上所有像素点分为变化与未变化两个类别。根据MRF理论有：

Y=arg max{P(Y)P(XD|Y)}

(1)

式中：P(Y)为类别标记的先验概率；P(XD|Y)是数据集中像素点的条件概率密度。

根据Hammersley-Clifford定理，可知吉布斯随机场(GRF)与马尔可夫随机场(MRF)等价，则式(1)值最大时等同于MRF能量函数最小。对于每个像素点xi，其能量函数UMRF(xi)定义为两部分组成：

UMRF(xi)=Uspectral(xi)+Uspatial(xi)

(2)

式中：Uspectral(xi)是光谱能量函数，描述了像素点xi的光谱特性，是该像素点的灰度统计描述；Uspatial(xi)是空间能量函数，描述了像素点xi与其所在邻域内其余像素点之间的类别依赖。

通常假定两时差值图像的灰度统计特性满足高斯分布，于是采用高斯分布来描述光谱能量函数Uspectral(xi)：

(3)

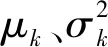
对于空间能量函数Uspatial(xi)，其根据中心像素点xi的标记与xi的邻域像素的标记情况来确定。且Uspatial(xi)满足：

(4)

(5)

式中：β为惩罚系数，通常β>0，其值由用户设定，通过取不同的β值可以控制邻域像素对中心像素的影响，调整空间上下文信息对变化检测过程的影响；Ni是像素点xi的邻域，通常采用二阶邻域，即对于每一个中心像素点周围有8个像素点；l(xi)和l(xj)是像素点类别标记，采用Potts模型来定义中心像素点与其邻域像素点类别标记关系I(l(xi),l(xj))；对于二值指示函数I(l(xi),l(xj))，当中心像素点标记与其邻域像素的标记相同时其值取为-1，否则取为0。

变化检测可视为典型的组合优化问题，其结果可通过迭代搜索算法所获取的全局或局部最优解来得到。使用ICM算法便可以获得式(2)的最优值。

2 基于变权MRF的变化检测

2.1 变权惩罚系数

在传统的基于MRF模型的变化检测算法中，Potts模型使用一个固定的惩罚系数β来计算空间能量函数。对于差值图像中所有的像素点来说，β的取值是相同的，这没有考虑差值图像中像素灰度值的分布特性，易造成差值图像中灰度值极大或者极小的像素点对于图像邻域信息的使用过度，从而影响变化检测精度。

对于差值图像首先使用FCM算法，将图像上的像素点初步分为两个类别，这会得到两个聚类中心。基于此结果，可以得到两个阈值H1、H2，因此可以将差值图像分为三部分。其中H1左侧为未变化类别，H1与H2之间为不确定类别，H2右侧为变化类别。H1与H2的计算方式如下：

(6)

式中：C1为未变化类别聚类中心；C2为变化类别聚类中心；Mmid为模糊C均值聚类后具有相同变化与未变化的隶属度的像素点所具有的灰度值，即该像素点属于变化类别与未变化类别的可能性相同，两种隶属度值均为0.5；α1和α2是两个常数，可以用来调节三个部分的面积。该划分如图1所示。

图1 变化、不确定、未变化类别划分示意图

在此基础上，根据差值图像中像素点的灰度值所在的区间，采用三个不同的表达式来计算所在区间的惩罚系数。于是修正式(4)中的固定惩罚系数β。其计算公式为：

(7)

式中：βm(X(i,j))是像素点位置为(i,j)的惩罚系数；Xmin和Xmax分别是差值图像中灰度最小和最大的值。

当图像中灰度值小于H1时，随着灰度值从H1减少到Xmin时，惩罚系数线性减小，这减小了具有相对较小的灰度值的像素对于空间邻域信息的影响，这是因为这些像素点有极大的概率保持不变。同理，当灰度值大于H2时，随着灰度值由H2增加到Xmax，惩罚系数线性减小，这减小了具有相对较大的灰度值的像素对于空间邻域信息的影响，这是因为这些像素点有极大的概率保持变化。对于灰度值处于H1与H2中间时，其属于不确定的类别，对于这类像素点采用一个固定的惩罚系数。以此重新定义了使用的空间信息的权重。

2.2 变权指示函数

在传统的基于MRF模型的变化检测算法中假设某个像素点常常与其所在邻域中的像素点具有相同的变化类别标记。然而由于外部条件所限，获得的遥感数据中包含大量混合像素。此外由于图像数据和算法本身的固有不确定性，差异图像的初始标记类别并不是确定的，这尤其体现在图像细节丰富的区域中。所以纯粹地将指示函数的值取为-1和0是不合适的，该操作会显得太绝对和不精确。本文对Potts模型进行修正，来重新定义邻域像素间的空间关系。

Foody[17]提出了一种基于熵的方法来度量邻域空间的像素标记的不确定性。采用该方法在模糊C均值聚类后，对于任意像素点可以得到其属于变化与未变化两个类别的隶属度。故可得像素点xj的熵，定义如下：

Ej=-uj,ch×log2uj,ch-uj,un×log2uj,un

(8)

式中：uj,ch和uj,un分别是该像素点属于变化与未变化类别的隶属度值。于是可以将式(5)修正为：

(9)

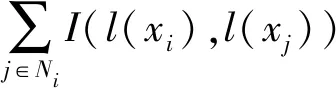
(10)

这样在计算空间能量函数时，可以充分考虑到邻域像素的类别标记的不确定性，使变化检测结果的过度平滑问题得到了很好的控制。故式(4)可以重新改写为：

(11)

2.3 算法描述

该变化检测算法的主要步骤概括如下：

1) 对配准、校正后的两时图像做差获得差值图像。

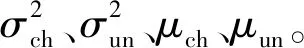
3) 使用变权MRF模型来修正空间能量函数Uspatial(xi)的计算，使用改进的变权惩罚系数和变权指示函数替换原始计算方式，重新定义空间上下文信息。

4) 使用ICM算法求解能量函数最小值，得到最终的变化检测结果。

该算法的示意图如图2所示。

图2 基于变权MRF变化检测算法示意图

3 实 验

3.1 实验数据及环境

实验使用的数据集为AICDDataset数据集和Szada数据集。AICDDataset为光学遥感模拟数据集，该数据集包含1 000组大小为800×600的两时图像及对应的变化检测参考图像，空间分辨率为0.5 m×0.5 m。Szada为真实遥感影像数据集，包含7组大小为952×640的两时图像以及对应的变化检测参考图像，空间分辨率为1.5 m×1.5 m。

分别进行如下实验：(1) 从2个数据集中随机选取2组数据，分别进行2组模拟实验、2组真实实验进行算法效果展示，所用的数据如图3所示。(2) 从AICDDataset数据集中随机抽取100组数据，比较本文算法与对比实验算法的效果。变化参考图中白色区域代表两时图像发生变化的位置，黑色区域代表未发生变化的位置。

图3 部分实验数据

实验所使用的数据均为经过精确配准、几何校正、辐射校正的数据，消除了由于外部不良因素导致的伪变化，通过MATLAB R2015b编制程序求解。

3.2 实验结果及分析

将本文算法与文献[10]和文献[15]的变化检测算法进行对比，以上4组实验结果分别如图4-图7所示。本文采用Kappa系数来评价变化检测的结果，其取值范围在[-1,1]之间，Kappa系数的大小反映了变化检测结果图与变化参考图之间一致性的程度，其值越接近于1，表示变化检测结果图与变化参考图的匹配程度越高。

图4 实验(1)结果图

图5 实验(2)结果图

图6 实验(3)结果图

图7 实验(4)结果图

上述实验的Kappa系数统计结果如表1所示。

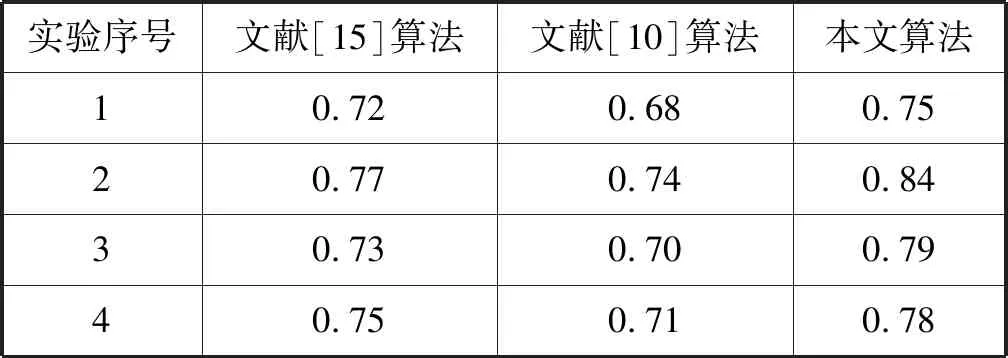
表1 Kappa系数统计表

从AICDDataset数据集中随机抽取100组数据进行实验，分别统计本文算法与对比实验算法的Kappa系数，结果如图8所示。

图8 Kappa系数对比图

上述两次实验结果表明，在绝大部分情况下，本文提出的变化检测算法与变化参考图具有最高的相似度，取得了比对比算法更好的变化检测结果。本文算法实现了对变化信息的有效提取，其含有较少的漏检和误检像素，对噪声等伪变化信息实现了良好的甄别，噪声点更少，实验结果也更平滑。

4 结 语

针对传统基于MRF模型变化检测算法在能量函数的计算中使用固定的惩罚系数和固定指示函数的问题，提出了一种基于变权MRF模型的无监督的遥感变化检测算法。该算法通过使用变权惩罚系数和基于熵的局部不确定邻域标记的变权指示函数，重新定义了空间信息权重和MRF模型中的邻域像素的空间关系，进而实现对空间能量函数的改造，优化了传统MRF模型。实验结果表明本文算法提供了比传统MRF模型更精确的变化检测，避免了变化检测的过度平滑问题。因此本文算法是一种可行、有效的变化检测算法。