基于分治思想和遗传算法的集装箱装载优化模型

贺红燕 赵红梅

(河北政法职业学院 河北 石家庄 050000)

0 引 言

随着全球化发展，规模化厂房和铁路等大型平台的远距离、跨区域布设已成为一种常见的经济现象。海上运输是大型平台的主要机动方式，其运输对象包括各类独立部门的设备器件以及对应的专业型雇员，是一个“人货同运”活动。为高效、快速和低成本地实施大型平台的远洋运输，需要对运输的资源与对象进行合理规划，调配装载方案，提高各部门到港后的快速作业反应能力,压缩船队的控制维护成本,实现载具的空间使用最大化。

求解满足特定要求的装载方案的问题被抽象为集装箱问题(Container Loading Problem,CLP)，在前人研究中被证明是NP-Hard问题[1-2]，即无法明确得到全局最优的形式解。研究者们往往以智能算法为工具，基于问题背景有所侧重地构造模型,从而求得符合自身需求的满意解。其中:Ramos等[3]提出了动态稳定性度量指标，以提高货物运输的安全性；程中文[4]和左先亮等[5]引入了三维空间分隔法，以实现装载空间利用率最大化；Monaco等[6]主要关心单个港口上装载所需时长的最小化；在多港口背景下，郑斐峰等[7]讨论了最小耗时的求解域建模，孙俊青等[8]则针对最高稳定性进行研究。先前研究中当CLP模型的自变量空间较小或优化目标单一时，采用经典搜索方法如树形搜索[9]、邻域搜索[10]、二次禁忌搜索[11-12]等能达到较好效果；当约束及优化目标复杂、搜索空间大时，采用遗传算法[13]、蚁群算法[14]、自适应细菌觅食算法[15]及其他改进启发式算法[16-18]能达到较好效果。总体而言，CLP模型求解方法较为灵活，立足模型本身特点，谋求在高收敛速度和高全局寻优能力两种性能上达到一个理想的均衡中值。

虽然前人研究丰富详实，但缺乏对人员、货物与船舶三者间匹配性约束的讨论，同时缺乏对运输成本、靠港后作业效率的考量，尤其在大型平台远洋运输背景中，应考虑通用货船只能运载设备，通用客船只能运载人员，而平台架设专用船舶则可同步运输人员货物的客观情况[19]。综上所述，本文基于大型平台远海运输现实情况，提出了靠港后快速作业反应、缩减船队规模以降低控制维护成本、最大化利用船舶空间三项度量指标，构造了多目标优化函数，建立了大型远洋作业中涵盖多类工种部门与船型之间的约束关系式。此外，本文立足于分治思想，基于对专用、通用两类船舶特性详细分析，对求解过程进行拆分，降低解空间复杂度，从而实现收敛速度的提升。

1 大型平台海运装载模型

基于大型平台运输的实际情况，本文构造模型时遵循以下假设：(1) 运输对象涉及多个工种部门，各部门具有不同的设备、人员;(2) 一个部门由多个分队组成，同一部门下的分队人员物资情况一致;(3) 各部门登船以分队为最小单位;(4) 当船舶剩余空间不足装载任何分队时，不可将分队拆散装入船舶中;(5) 登船的前后顺序不影响该船只的装载能力;(6) 执行任务的专用船舶数目有限，而通用船只数目可依需求增减;(7) 必须在一次行动中将所有部门装载完毕，不可反复、多次运输;(8) 可以将设备与人员分离运输，但仍必须以分队为最小单元;(9) 当同一分队下的设备和人员同时在一艘船只上运输时，分队在靠港后可直接执行作业任务；(10) 当设备和人员分离运输时，必须先将两者结合为整体，需要花费一定的反应时间。

考虑到这一问题的特点，本文在建立模型时，以装载方案为自变量，采用自然数矩阵XC×2N进行描述：

式中：N为待运输的部门种类数;C为船舶数目。矩阵中的元素xi,j表示第i艘船只装载第j类部门的分队数量,采用2N的列数是由于每一类部门均可拆分为人员及设备两部分。

1.1 模型优化目标设计

结合实际环境，本文设计了三类优化指标，并通过加权求和的方式组合为多目标优化函数。

1) 空载率。远洋运输条件下，载具资源十分昂贵，但由于假设(3)和假设(4)，船舶难以实现满载，必须考虑如何用有限的空间运输尽量多的货物。对此，本文提出了“空载率”指标，用于量化对载具资源的利用程度，公式如下：

(1)

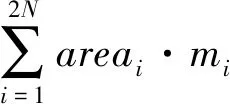
2) 船队规模。远洋航行过程中，运输船队常保持一定队形以实现相互补给、协同交流，有效规避海运事故或海洋犯罪事件；另外，船队中的每艘船只本身都需要消耗一定的油料、物资。因此，船队的规模越大，指挥、维护船队的耗费越大，运输的成本越高，因此，在制定装载方案时，必须考虑缩小船队规模，减少不必要的运输成本。对此，本文提出“船队规模”指标，用于量化描述运输装载方案实施耗费的成本。

(2)

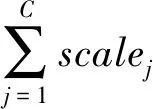
3) 人货分离率。根据假设(9)和假设(10)，为使各部门在靠港后尽快投入作业任务，在运载时应尽量使得同一个分队下的人员及设备装载在同一艘船只上，减免出现人货分离运载的情况。对此，本文提出了“人货分离率”指标，用于量化描述某装载方案下的快速反应作业能力。

(3)

式中：∑com_uniti表示装载于同一艘船只上的同属一个分队的人员、设备的分队数目;ZJZ表示分队总数。式(3)的取值越小，则证明人员与设备越集中，作业反应时间越短，效率越高。

基于上述三个指标，通过加权求和的方式组成多目标优化函数：

f=w1·Rkz+w2·Rgm+w3·Rfl

(4)

式中：w1、w2、w3分别为各个指标权值。本模型的目的就是求得使式(4)取值尽可能小的一组解。

1.2 模型约束函数设计

本文主要从船舶可装载面积限制、船舶可装载重量限制、待运输单元总体恒定限制、船舶与部门相互匹配限制考虑，制定了以下约束条件：

(5)

(6)

(7)

(8)

式(5)表示分配给j船只的所有单元的占地面积之和不大于j船只的最大可运输面积;式(6)表示分配给j船只的所有单元的重量之和不大于j船只的可承重极限;式(7)表示第i类部门在本分配方案下可以全部分配完毕;式(8)表示第i类部门不可被装载在与其不匹配的运输资源上。

综上所述，在N类部门、C艘可用船只的情形下，本模型构造了4N个不等式约束及2C个等式约束。

1.3 模型复杂度分析

根据上述分析，模型的公式化表述如下：

minf(XC×2N)=w1·Rkz+w2·Rgm+w3·Rfl

(9)

对N类部门、C条船只，上述模型解可能的搜索空间大小为：

(10)

式中：mi为第i类部门的分队数目。

(11)

根据模型的公式化表述，构造拉格朗日函数如下：

f(X)+μTh(X)+λTg(X)

(12)

假设▽xxL(X*,λ*)正定，要获得局部最优值，必须符合的KKT条件为：

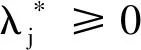
(13)

显然，由于自变量维度大、等式不等式约束数目多，使拉格朗日算子复杂，即使作光滑化处理，依然不具备好的凸优化方法应用条件，且▽xxL(X*,λ*)正定条件严格，难以给出形式解。

综上所述，模型复杂度较高，一方面，自变量搜索空间广，无法通过简单的枚举求解;另一方面，繁琐的拉格朗日函数难以用经典凸优化方法求解。上述分析结论反映了模型NP-Hard特性。因此，本文首先基于分治思想对自变量空间进行降维，而后采用遗传算法快速收敛至理想的可行解。

2 基于分治思想和遗传算法的求解

2.1 分治方法的应用效益分析

本文构建的模型较为复杂，对此引入了分治与遗传算法两种求解方法。分治是指将耦合度较高的复杂问题分解为多个相对简单的可独立求解的子问题，通过将多个子问题的解组合构造出原问题的一个可行解。为证明分治思想在大型作业平台远海运输装载问题上的可行性，基于背景条件及模型的数学化描述，给出以下分析：

1) 装载计划中，应优先使用专用船舶。由于专用船舶具备同时装载设备与人员的能力，可以完整运输一个分队，不占用多的运载空间、无须扩展船队规模；相对地，由文献[19] ，通用船只运载能力往往受限，客货分离特征明显，人货结合度低，且有可能需要较大船队规模完成运输任务。因此，在装载规划中，专用船舶的使用优先度高。当专用船舶有剩余空间时，应优先装载专用船舶。

2) 由于需装载对象总量大于专用船舶承载量，结合优先装载专用船舶的分析，有以下推论：针对专用船舶的装载规划问题，在船队规模、人货分离率两个指标上可达最优边际(规模压缩至最小，为全体专用船舶的数目总和，是固定值；采用人货结合形式装载，分离率为局部最小值)。

因此，在讨论整体装载问题时，考虑到专用船舶装载部分本身可以达到边际最优的解。在求解时，可以将该部分独立分离，构造子问题(1)——“专用船舶装载规划”。

3) 剩余需装载对象以三大指标构造的混合目标函数装载到通用船舶上，可构造子问题(2)——“通用船舶装载规划”。

两个子问题的模型为原模型的调整变形，对子问题(1)的变形，模型如下：

minf(XnZC×N)=w1·Rkz+w2·Rfl

(14)

式中：nZC为专用船舶数量。

对子问题(2)，其模型如下：

minf(XnTC×2nSN)=w1·Rkz+w2·Rgm+w3·Rfl

(15)

式中：nTC为通用船舶数量;nSN为剩余的待装载人员、货物总和;smi为i类部门剩余的数目。

采用分治理论后，搜索空间大小为：

(16)

搜索空间数量级为：

(17)

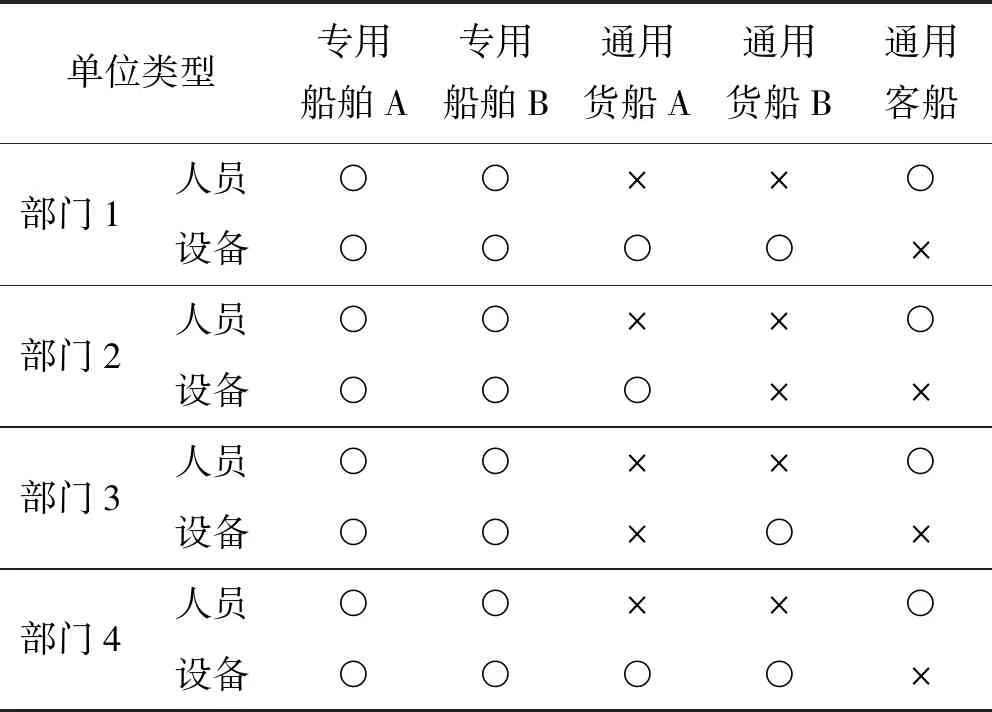
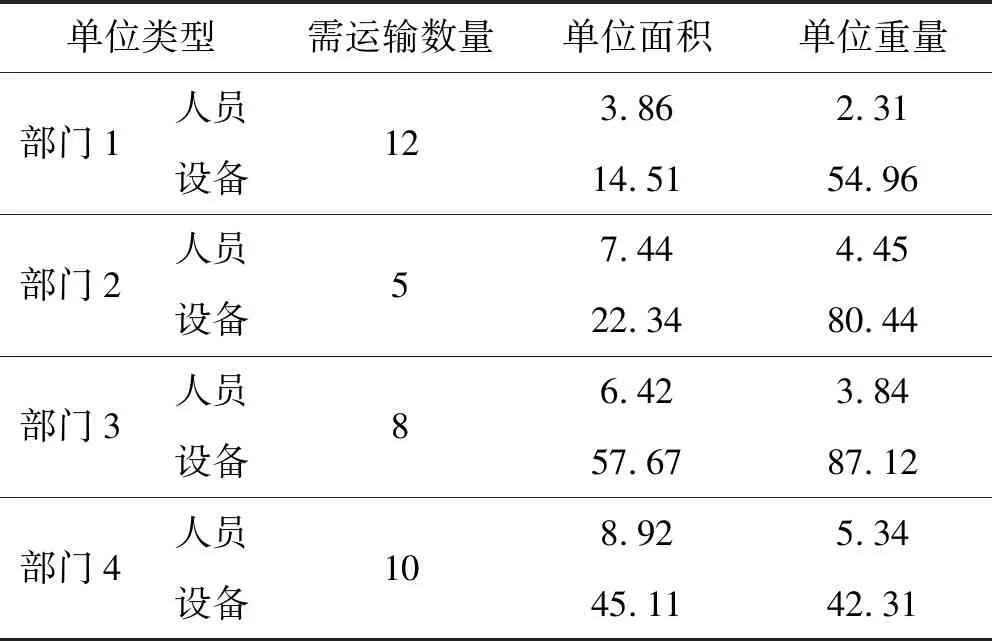
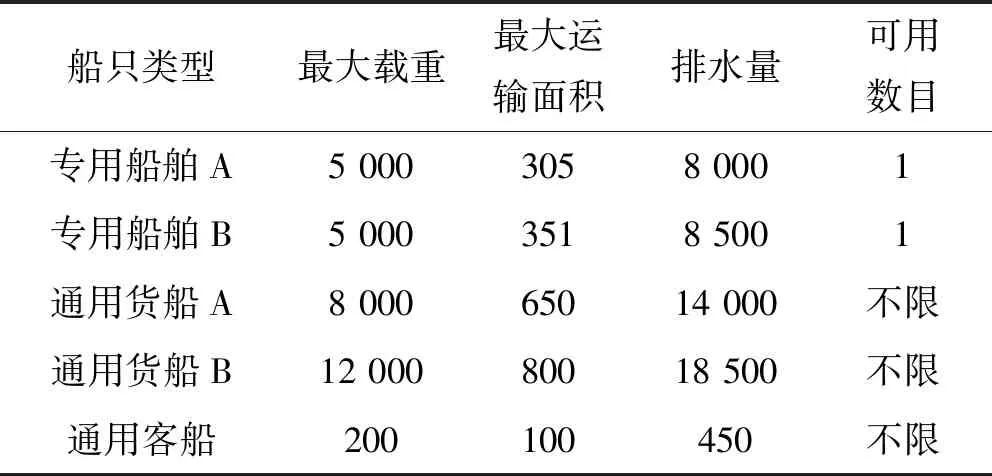
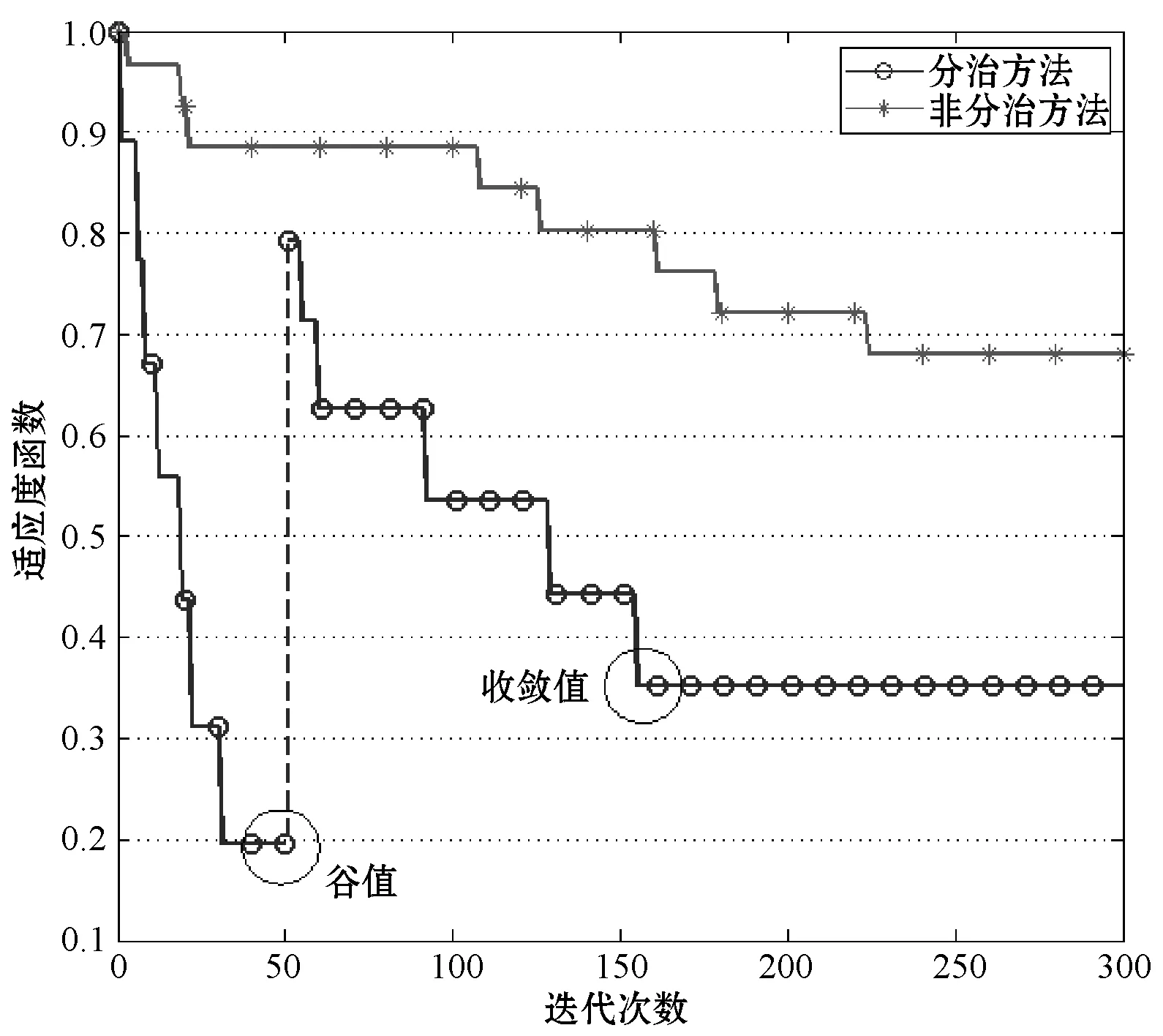
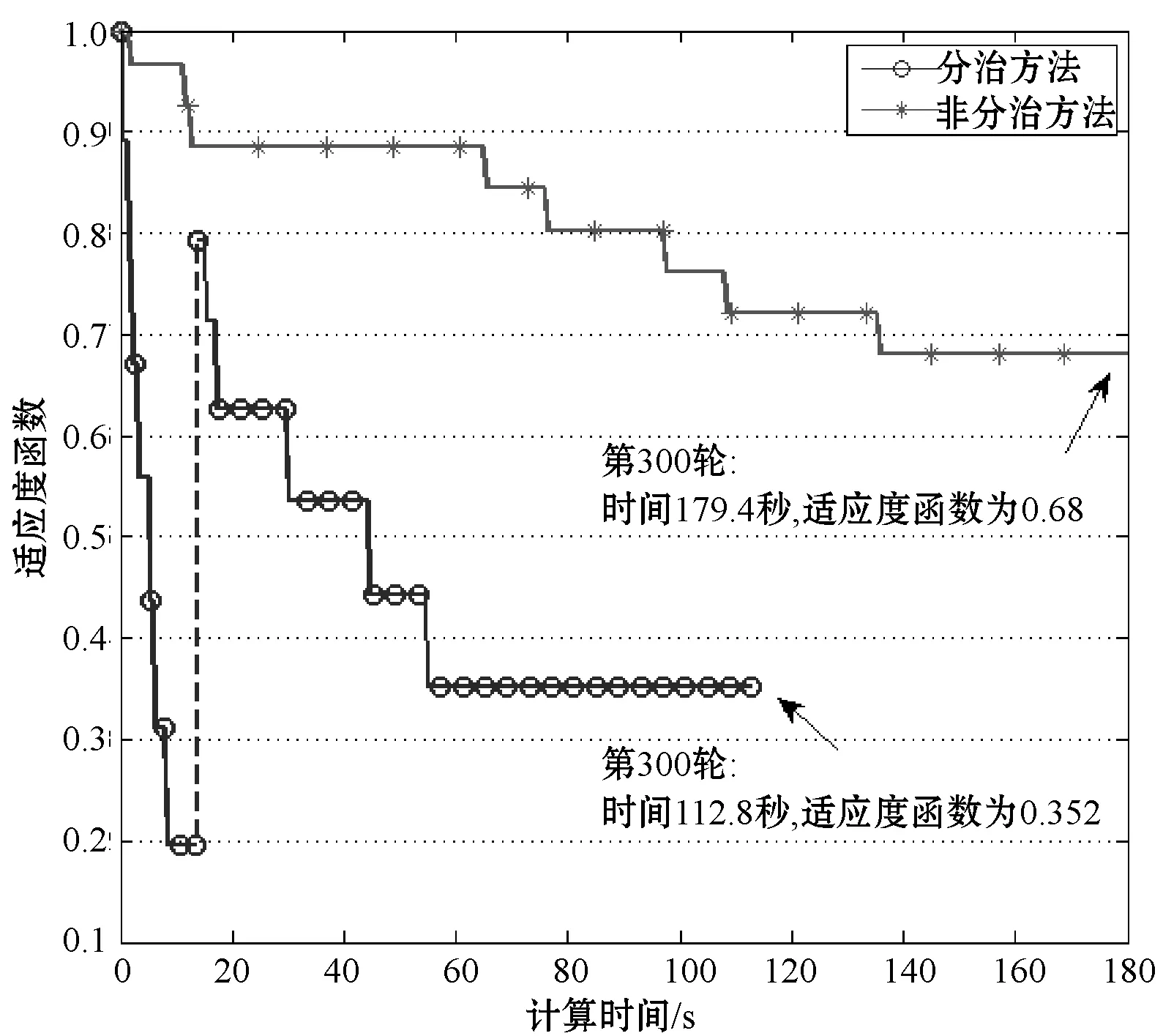
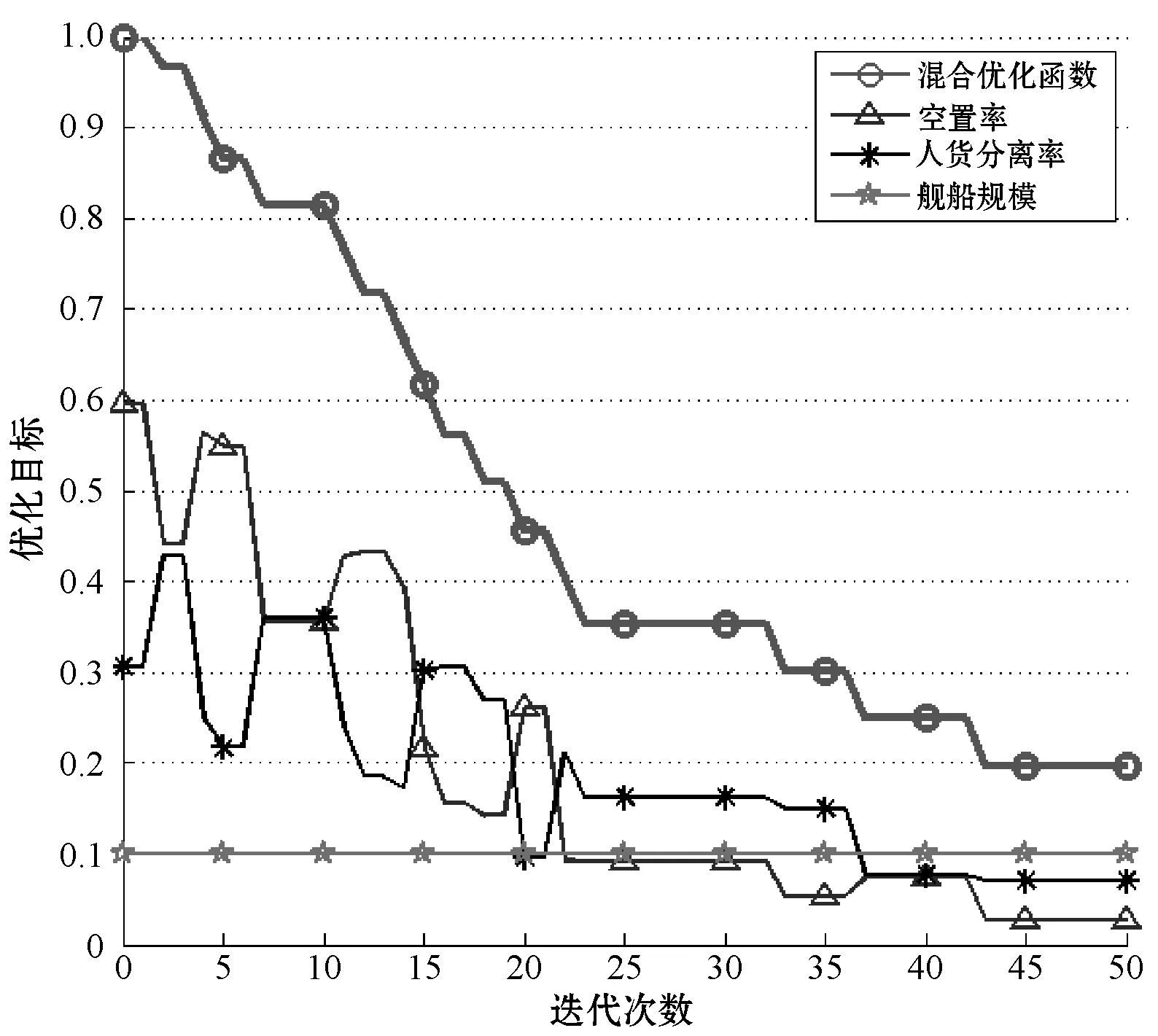
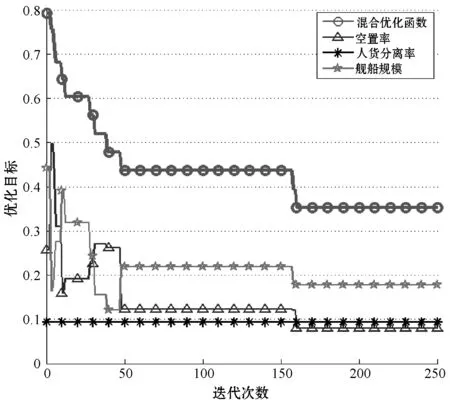
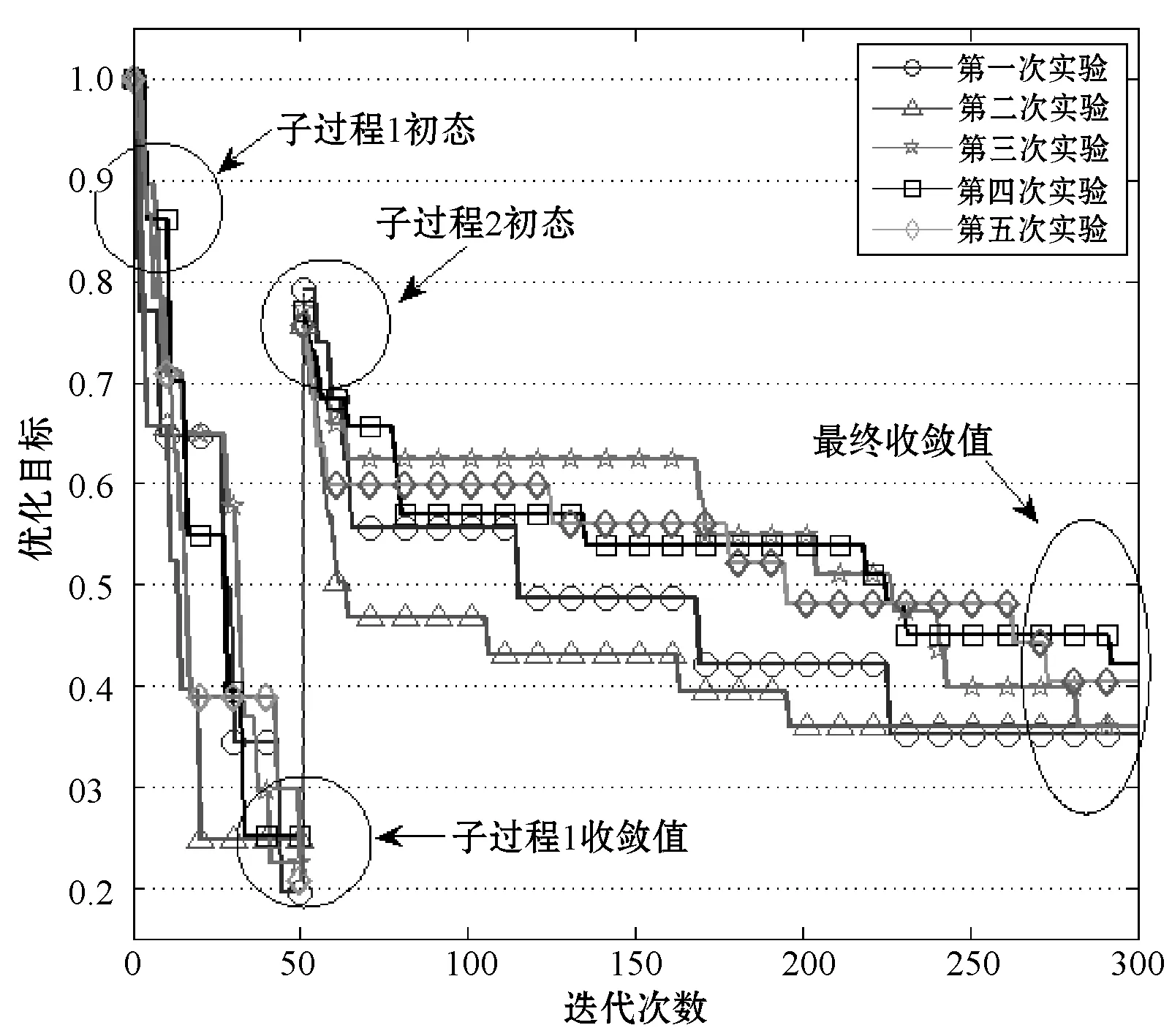
式中：max(·)运算表示取括号内元素的最大值。由于nZC

O2

(18)

即分治方法实现了解空间的收缩。

在通过分治将原模型分解为两个子模型后，本文采用了遗传算法进行解的寻优。遗传算法作为一种最常用的智能仿生算法，具有设计简单、收敛较快、计算复杂度低等优点。算法自然基因编码规则令第i行第j列的值编码值=自适应变量矩阵X中对应的元素xij。

令算法适应度函数等同两类子问题优化函数，对子问题(1)：

fitness=w1·Rkz(XnZC×N)+w2·Rfl(XnZC×N)

(19)

对子问题(2)：

fitness=w1·Rkz(XnTC×2nSN)+

w2·Rgm(XnTC×2nSN)+w3·Rfl(XnTC×2nSN)

(20)

算法中遗传算子采用交叉、变异两类，基于算子变换产生的子代可实现对自变量矩阵空间的覆盖。

综上所述，采用分治方法与遗传算法相结合的求解方法，从理论上得证能显著收缩解的搜索范围，显著提高求解效率。

2.2 分治方法的适用性分析

根据式(10)，本文构造的模型为NP-Hard问题，难以求出公式化完备解，无法确保解的全局最优性。采用智能算法求解该类型问题，得到的解是邻域内极小点，具有局部最优特性。

利用分治算法将问题拆分为两个子问题，子问题的求解相互独立，子问题(1)的解构成了子问题(2)的条件。子问题(1)与子问题(2)都是可证具有全局优化特点的解，因此当两者相互合并构成的解必定是在子问题(1)的解的优化方向的一个极值点，即该解在邻域范围内最优，为局部最优点。

综上所述，采用分治方法后取得的解与采用分治方法前的解一致，均为局部最优解。

2.3 仿真结果分析

基于实际情况设计仿真场景，表格中数据由一次铁路组件远海安装的航运实际数值简化得到。表1展示了各部门与船舶的装载匹配关系；表2展示了需要装载的各部门数量、占地面积及重量；表3展示了各船只的最大载重量、最大运载面积及排水量及可使用数目。实验中目标函数的优化参数权值采用平均配置(子问题(1)为1/2，子问题(2)为1/3)。

表1 各部门工种与船舶装载匹配关系

注：“○”表示可以装载，“×”表示不能装载。

表2 各部门工种数量、占地面积及重量

表3 各船舶最大载重量、运输面积及排水量

设计遗传算法种群数量为200，种群单基因点发生交叉、变换的概率分别为0.19和0.08。在有限次迭代下分析算法适应度函数及三项优化指标变化情况。

1) 模型收敛速度检测实验。以一定迭代范围内适应度函数的变化情况描述模型的收敛速度，两种求解方法的适应度函数变化如图1所示。

图1 适应度函数-迭代次数变化情况

可以看出，未采用分治方法适应度函数折线下降平缓，在300次迭代中未能收敛到理想值。采用分支方法后，适应度函数折线下降速率快，其中，从起始点到谷值为分治子问题(1)，总迭代次数为50，目标收敛值为0.195 8。随后进入分治子问题(2)，总迭代次数为162，收敛值为0.352 0。显然，不采用分治方法，在复杂度高问题的求解中，无法在较少迭代次数下完成收敛，采用分治方法后，可以更快求得理想解。

以计算时间为横坐标，分析分治方法对模型求解速率的性能提升，结果如图2所示。

图2 适应度函数-计算时间变化情况

不采用分治方法进行300次迭代运算所需时间为179.4秒，在相同计算条件下，采用分治方法仅需112.8秒，总运算时间减少了约37.1%。

2) 多目标优化函数效果检测。优化目标函数的三类优化指标随迭代轮数变化如图3和图4所示。

图3 子问题(1)各优化目标变化情况

图4 子问题(2)各优化目标变化情况

对图3分析可得，子问题(1)目的是以专用船只对货物进行尽可能多的装填。该过程中，舰队规模为常数(舰队规模=专用舰船总数)，空置率及人货分离率交替震荡(采用不同的货物组合形式)，在遗传算法适应度函数标准下，控制该过程总体呈下降趋势。综合三类优化参数，混合优化函数保持单调下降。该结果表明，分治子问题(1)可实现较为快速有效的收敛。

对图4分析可得，分治子问题(2)目的是对剩余货物采用尽可能少的通用船只进行完全装载。由于通用船受船只类型本身人货全部分离的约束，因此优化目标人货分离率为常数；另一方面，空置率与舰船规模交替震荡；总优化目标函数呈下降趋势，在160次迭代后达到满足要求的理想解。同样地，该结果表明分支问题(2)可实现较为快速有效的收敛。

3) 蒙特卡洛测试鲁棒性及全局最优搜索能力。在相同条件下，多次仿真的适应度函数变化折线如图5所示。

图5 多次蒙特卡洛实验的收敛情况

由于本文采用遗传算法引入了随机性(初始化的随机性及遗传算子的随机性)，使求得的最终解存在一定的方差。为避免随机性对最终结果的影响，提高解的强健与稳定能力，本文探索了通过多次重复实验(蒙特卡洛原理)获取最优解的方法。图5所示为重复次数为5时的实验结果，由于采用随机初始化策略，每次重复中的初态有所差异，进而影响了子问题(1)的收敛值及子问题(2)的初态，最终影响子问题(2)的收敛值。上述现象的问题根源在于，模型采用的分治方法牺牲了全局最优性换取了时效性，因此在不同的初态下，陷入了不同的局部极值。

为对抗上述局部极值现象，本文采用多次重复实验(蒙特卡洛)方法，并在仿真中起到了一定效果。表4记录了多次独立的重复实验的适应度最小值。

表4 蒙特卡洛实验下的适应度函数最优值变化

显然，重复次数大于5后，可以大概率取得较为稳定的理想解。这是由于每次重复实验都通过随机方式生成系统初态，当初态种群中能够包含可以达到最优值的初态时，后续算法可以快速检索并收敛到最优值。随着重复次数增加，初态种群的规模增长，种群中包含最优值初态的可能性就越高。

综上所述，通过重复实验方法可以增强模型的鲁棒性。

4) 应用评价与效能分析。根据本文构建模型，对仿真问题求解，多目标函数与单目标函数在权重均等的情况下，求得的解如表5所示。

表5 求解情况

显然，本文构造的模型采用多目标优化函数，与单目标相比，该模型选择了船只数目少、排水总量低、空置率低的一组解，而其他模型只追求单一标准下的最优而致使其他指标过大，边际低收益状况明显。因此，仿真结果表明本文模型可以权衡靠港后快速作业反应、缩减船队规模以降低控制维护成本、最大化利用船舶空间三项度量指标。

3 结 语

本文针对大型平台远海运输装载方案规划问题，提出了一种新的CLP模型。模型以空载率、船队规模、人货分离率为优化指标，考虑了船舶承载面积、承重极限，以及与不同部门的匹配关系等约束。针对模型复杂度较高、难以用经典方法求解的问题，利用分治思想将模型拆分后用遗传算法寻得局部域最优解。仿真实验表明，分治方法可显著提高收敛速度，多目标优化函数可较好地反映实际需求，通过多次蒙特卡洛重复实验可增强鲁棒性，稳定地取得理想解，且解具有对多目标权衡的特性，能够满足现实任务需求。