Spectral Properties of an Energy-Dependent Hamiltonian

Pierre Chau Huu-Taiand Bernard Ducomet

1 CEA,DAM,DIF,F-91297 Arpajon,France.

2 Universit´e Paris-Est,LAMA(UMR 805),UPEMLV,UPEC,CNRS,61 Avenue du G´en´eral de Gaulle,F-94010 Cr´eteil,France.

Abstract.We study spectral properties of a quantum Hamiltonian with a complex-valued energy-dependent potential related to a model introduced in physics of nuclear reactions[30]and we prove that the principle of limiting absorption holds at any point of a large subset of the essential spectrum.When an additional dissipative or smallness hypothesis is assumed on the potential,we show that the principle of limiting absorption holds at any point of the essential spectrum.

Key words:Non-selfadjoint,complex potentia,dissipative,limiting absorption principle,spectral singularity,energy dependent potential.

1 Introduction

Our goal in this paper is to study spectral properties of the energy-dependent operator

in R3,whereΔis the Laplacian in R3,ρ∈C is the spectral parameter(the associated energy isζ=ρ2),U0denotes multiplication operator by the function U0(x):R3→R and U(ρ):=V(ρ)-iW(ρ)denotes multiplication operator by the function U(x,ρ):R3×C→C with U(x,ρ):=V(x,ρ)-iW(x,ρ).

We also suppose that V and W are factorized as follows

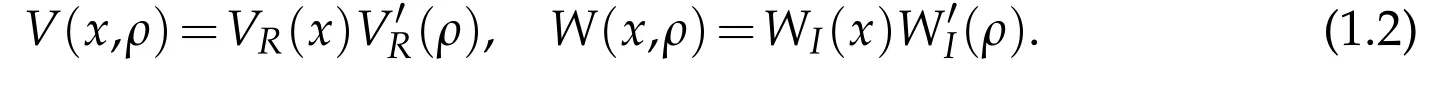
Such an operator appears in physics of nuclear reactions[7]:U0is a(possibly long-range)external potential(Coulomb)and U(ρ),the energy-dependent part(possibly long-range),is called Optical Potential in this context(see[2]for a physical introduction).In[3]spectral properties of a related 1D model relying on specific space-energy hypotheses for V and W(specified in[30])have been studied and our aim in the present paper is to generalize this study to the physical dimension d=3 when dissipation may be possibly taken into account.

It is worth to observe,using inverse Laplace transform that the operator H(ρ)can be derived from a Schr¨odinger equation perturbed by a non-local term involving a convolution with respect to time leading to the problem

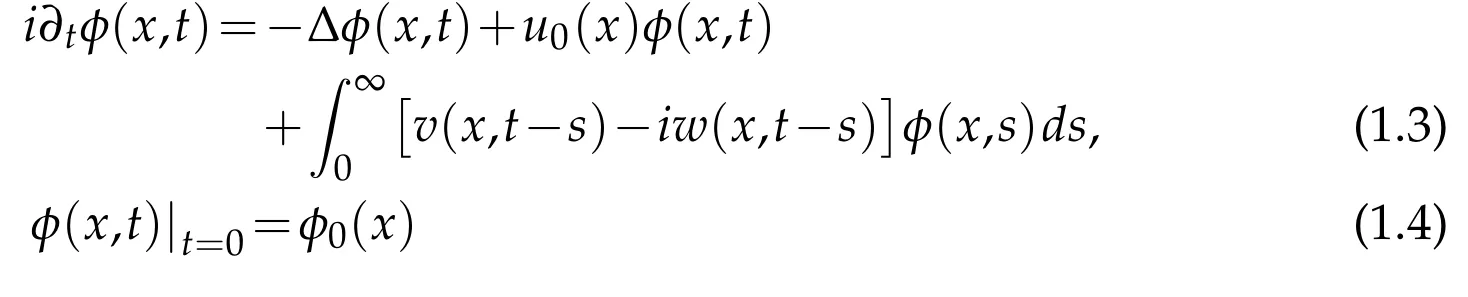
for(x,t)∈R3×R+and for real valued u0,v and w,where v and w satisfy a causality assumption

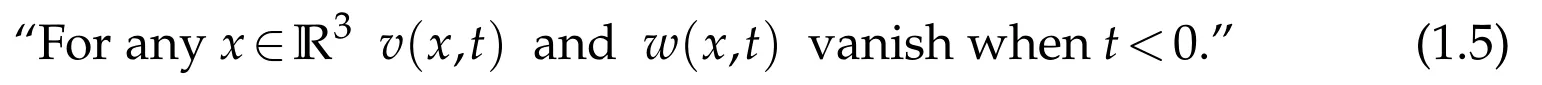
It will be the purpose of a future work[4]to study solutions of(1.3)-(1.4)and their large time asymptotics.Just mention that this problem has yet be studied by Mochizuki and Motai[29]in the local case v(x,s)-iw(x,s)(x))δ(t-s).

We make the following hypotheses on functions U0(·)∈C∞(R3,R),V(·,ρ)∈C∞(R3,R)and W(·,ρ)∈C∞(R3,R),which comply with the expressions given in[30].

Condition 1.There exist constants Cα＞0,a0＞0,a1＞0,a2＞0 and R0＞0 such that uniformly in the positive half-plane C+≡{ℑm(ρ)＞0}and for anyα∈N3and for|x|≥R0

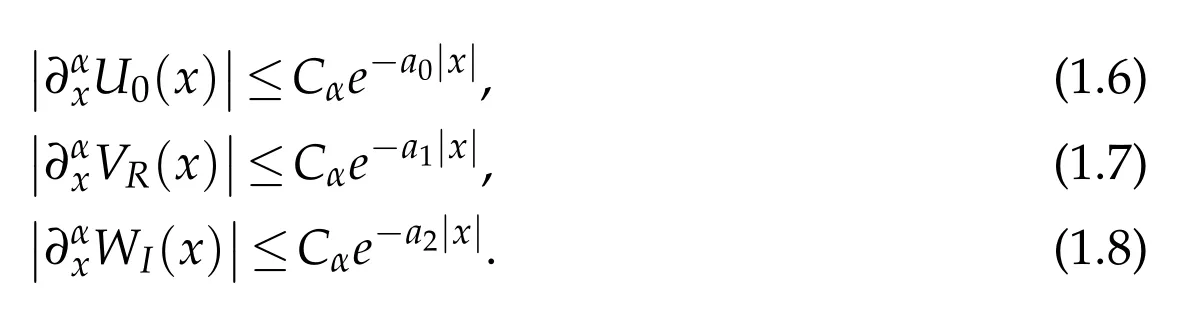
In the following we will also use less restrictive decay conditions on U0and U(ρ).

Condition 2.There exist constants C＞0,δ＞0 and R0＞0 such that for|x|≥R0

where〈x〉=(1+|x|2)12,and

uniformly in the positive half-plane C+≡{ℑm(ρ)≥0}.

We also need analytic assumptions in energy.

Condition 3.There exist a finite family F:={ρj}j=1,...,Nof points belonging to the open negative half-planesuch that(ρ)and(ρ)are holomorphic in CF.Moreover(ρ)and W′I(ρ)are holomorphic and uniformly bounded in the positive half-plane:there is a＞0 such that

Finally we consider the smallness condition.

Condition 4.We say that the potential q(x,ρ)is small if

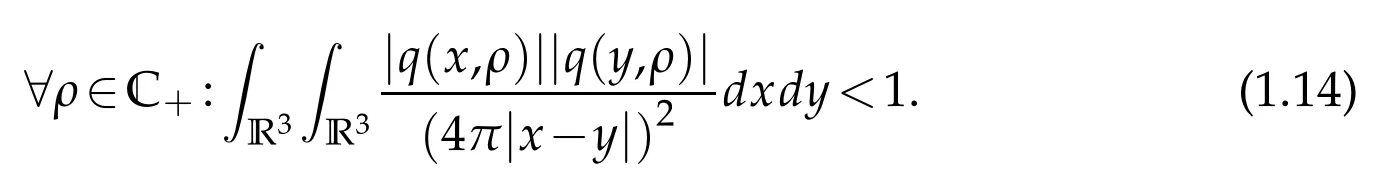
Let us begin with some motivations for this work.A lot of articles have been devoted to the study of the discrete spectrum of self-adjoint Schr¨odinger operators(see Reed and Simon[37]for an extensive review of this problem)including its localization and(sharp estimates on)the number of eigenvalues.In the nonselfadjoint case some informations are known[5],and it is interesting to extend the results to energy-dependent potentials.This will be the purpose of the first part of this paper.

A second motivation concerns the essential spectrum.Let u be a bounded solution u of the time-independent Schr¨odinger equation

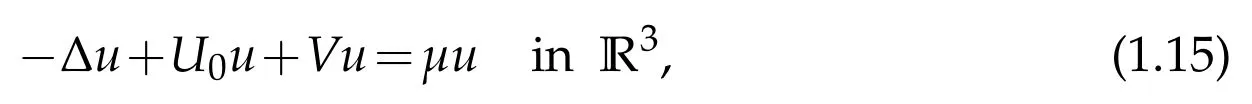
whenμ=|k|2and V is real-valued and energy independent,in the form of a distorted plane wave

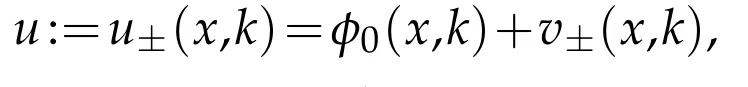
whereφ0is the plane waveφ0(x,k)=eik·xand where both u±(x,k)and v±(x,k)behave like O(|x|-1)at infinity.

One knows that(1.15)has a unique solution obtained by solving the Lippman-Schwinger equation

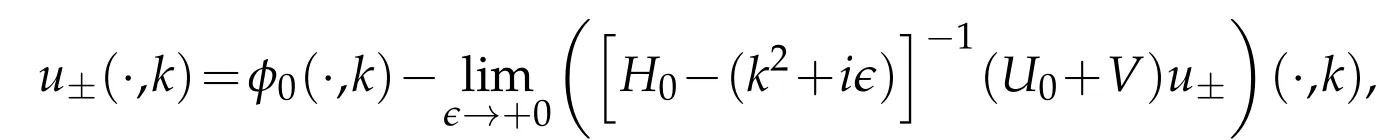
or explicitly[36]

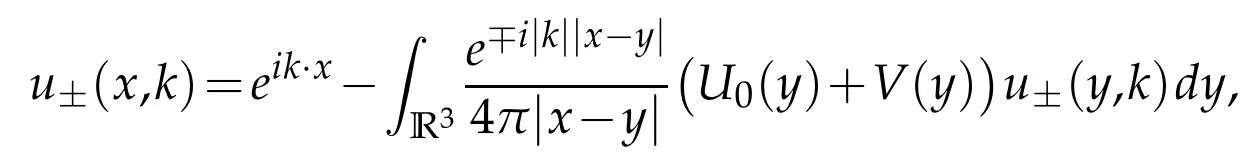
provided that the Sommerfeld radiation condition

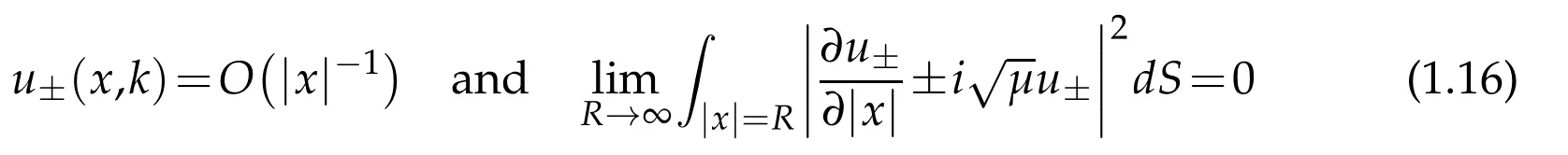
is satisfied.

However,when V is complex-valued,Naimark[31],Schwartz[45]and Pavlov[33-35]observed that such a radiation condition is not always sufficient in order to insure uniqueness.In that non-selfadjoint framework,uniqueness is expected to hold only forμ/∈ΣwhereΣis a subset of R+and an important goal is to obtain informations on the location and size ofΣ.Mochizuki[27]and Saito[46]gave such informations for non energy-dependent potentials and our second purpose in this work will be to extend them to our energy dependent case.More precisely let us put H0=-Δ+U0and denote the resolvents of H0and H(ρ)by R0(ρ)=(H0-ρ2)-1and R(ρ)=(H(ρ)-ρ2)-1.Our main result is the following.

Theorem 1.1.Suppose that Conditions 2 and 3 are satisfied,and denote by K the region of the complex plane

with 0＜v1＜v2＜∞.

(i)If I∩Σ=∅,the Limited Absorption Principle(LAP)holds i.e.:

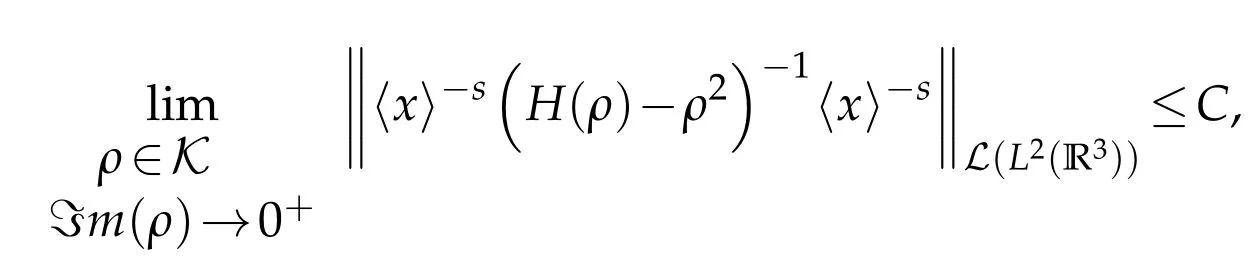
(ii)If U0+U(ρ)satisfies Condition 4 one can takeΣ=∅and the LAP holds at any point of R+.

(iii)If the dissipative condition

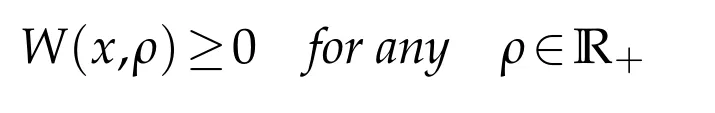
is satisfied,and if the real part V(x,ρ)of U(x,ρ)satisfies the smallness Condition 4 one can also takeΣ=∅and the LAP holds at any point of R+.

(iv)If the dissipative condition

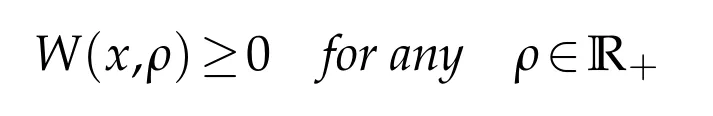
is satisfied,and if the imaginary part W(x,ρ)of U(x,ρ)is replaced by gW(x,ρ)where the coupling constant g＞0 is small enough,one can also takeΣ=∅and the LAP holds at any point of R+.

Remark 1.1.1.The possible existence of spectral singularities was acknowledged in the 1D case by Naimark[31],Lyantse[24,25],Pavlov[33-35],Krall[21],Folland[8]and Hruˇsčev[14].

2.Point 1 of Theorem 1.1 shows that the LAP holds for almost anyρ∈R+(i.e.the setΣis not“too big”).Moreover points 2,3 and 4 rule out the presence of spectral singularities embedded in the continuous spectrum when suitable smallness or dissipative conditions hold then the LAP holds for any ρ∈R+.

Let us give a few informations about the related literature.Studies of the 1D non-selfadjoint case go back to the pioneer work of Naimark[31].Among his followers,let us refer to the works of Lyantse[24,25],Pavlov[33-35],Krall[21]and more recently Folland[8]and Hruˇsčev[14].

Concerning the 3D non-selfadjoint case let us quote related papers by Kato[18,19],Mizohata and Mochizuki[26],Iwasaki[17],Mochizuki[27,28],Mochizuki and Motai[29],Ikebe[15],Ikebe and Saito[16],Saito[46].Bounds on the discrete spectrum are proposed by Abramov,Aslanyan and Davies[1],Frank,Laptev,Lieb and Seiringer[11],Laptev and Safronov[23],Wang[49,50],Safronov[44],Stepin[47,48],Enblom[6],Frank[9,10,12].For energy-dependent potentials let us mention among few studies concerning specific types of energy dependence,the case U0(x)=0,U(x,ρ)=-iρW(x)studied by Nakazawa[32],and various works corresponding in fact to a damped equation in the space-time domain(see for instance Iwazaki[17],Mochizuki[28]).Finally more recently Royer[39-42]investigated resolvent estimates for the dissipative Helmholtz equation,using Mourre’s method,in the semiclassical framework.

The plan of the paper is as follows:in Section 2 we study the discrete spectrum of H and give informations on the position and number of eigenvalues in the short range case.Section 3 contains a priori estimates necessary to analyze the continuous spectrum of H and to prove the Limiting Absorption Principle(first part of Theorem 1.1)and we also investigate the setΣof spectral singularities.The last part(Section 4)concentrates on the case where the potential is small or dissipative(second,third and fourth points of Theorem 1.1).

2 Localization and number of eigenvalues

In this section we assume that U0and U(ρ)are short range and suppose for simplicity that U0≡0.The free operator is H0=-Δwhich is self-adjoint on L2(R3)with domain D(H0)=H2(R3)andσess(H0)≡σac(H0)=[0,∞).The free resolvent R0(ζ)=(H0-ζ)-1is,forζ/∈[0,∞),the integral operator with kernel

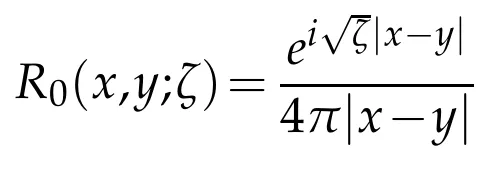
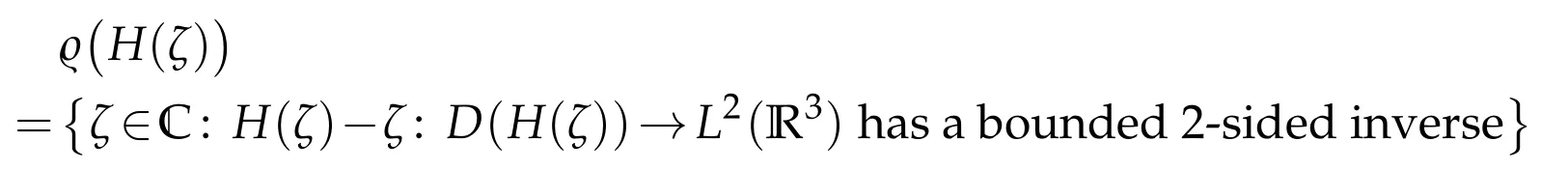
its spectrum is defined byσ(H(ζ)):=Cϱ(H(ζ)).

The essential spectrum of H(ζ)is obtained as usual by the Weyl’s prescription[13]

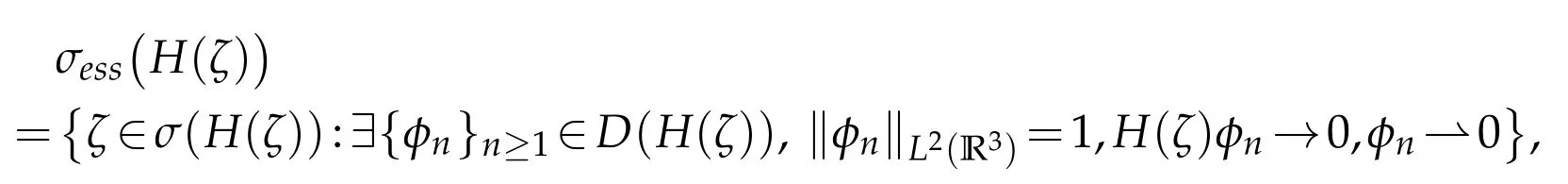
and the set of eigenvalues of H(ζ)is the point spectrum denoted byσp(H(ζ)).One also denotes byσc(H(ζ))the continuous spectrum of H(ζ)and byσr(H(ζ))its residual spectrum,always absent in the self-adjoint case(see[37]).

We have first an extension of a result by Stepin[48].

Lemma 2.1.Suppose that Conditions 1 and 3 are satisfied.

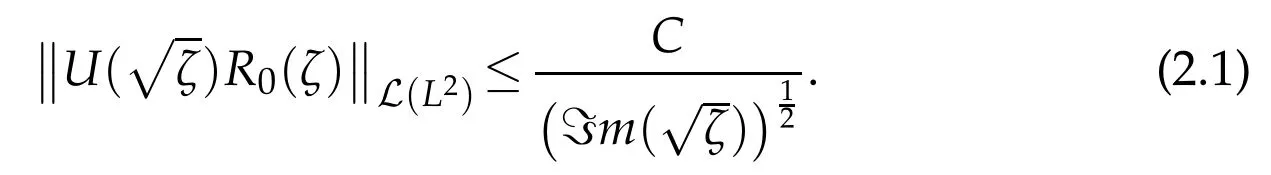
2.The integral operatorΓ(ζ):=R0(ζ)U()R0(ζ)with kernel

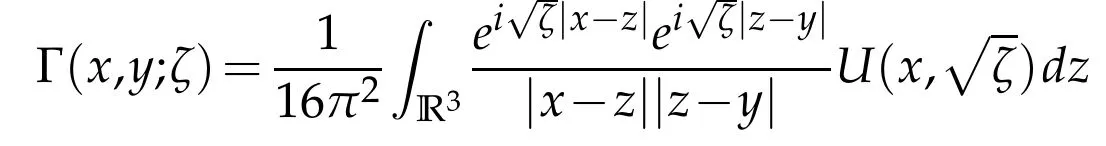
is also Hilbert-Schmidt and its operator norm satisfies

where the function h is the inverse of sseaswith a=max{a1,a2}and the constant C′＞0 is

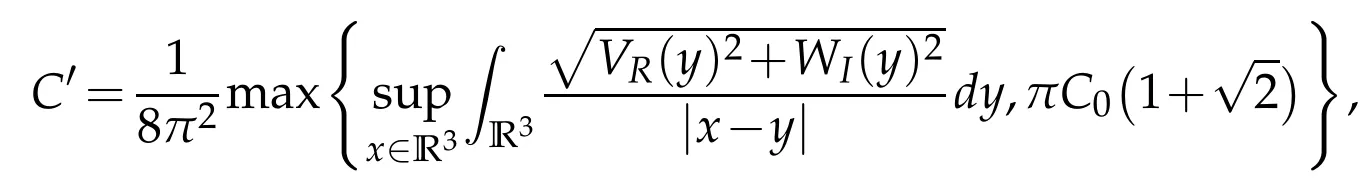
and C0=Cα||α|=0in Conditions 1 and 3.

Proof.

1.Denoting by‖‖HSthe Hilbert-Schmidt norm,we have

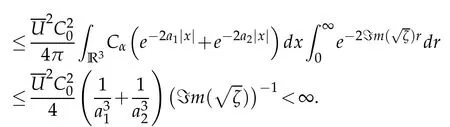
As‖·‖L(L2)≤‖·‖HS,estimate(2.1)follows.

2.Letν=mint∈[0,1]|x+s(y-x)|and let E(x,y;r)be the ellipsoid of revolution with foci x and y and semi-axes r andwith.One checks that the estimate

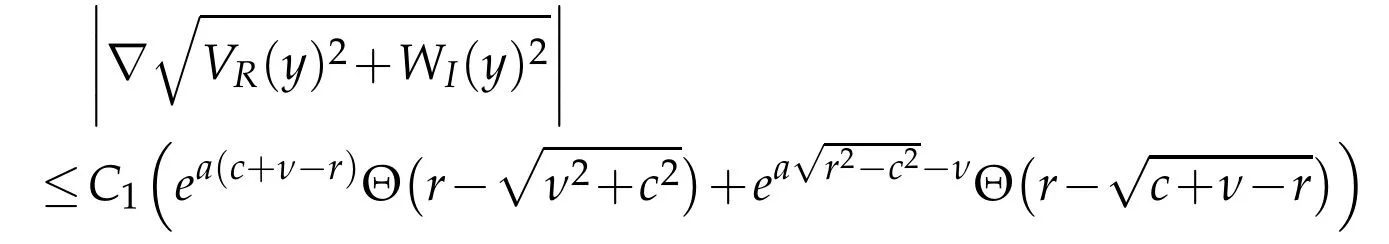
with a=max{a1,a2},holds on E(x,y;r).This implies the inequality

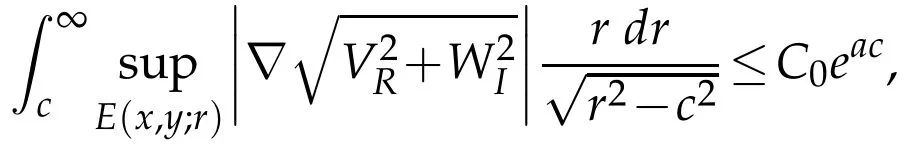
and estimate(2.2)follows.

We are now in position to give an approximate localization of the eigenvalues,following Frank[9].

Proposition 2.1.Suppose thatThen every eigenvalue λ∈C[0,∞)of H satisfies

where the constant D(γ)＞0 is independent of the potential U(x,ρ)=V(x,ρ)-iW(x,ρ).

Proof.The proof relies on the Birman-Schwinger principle.Ifλis an eigenvalue of H,denotingandχ:=Yψ∈L2(R3),we get

so

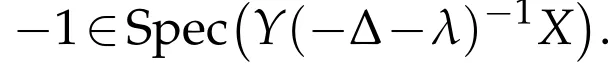
One observes that(2.3)holds provided we show the estimate

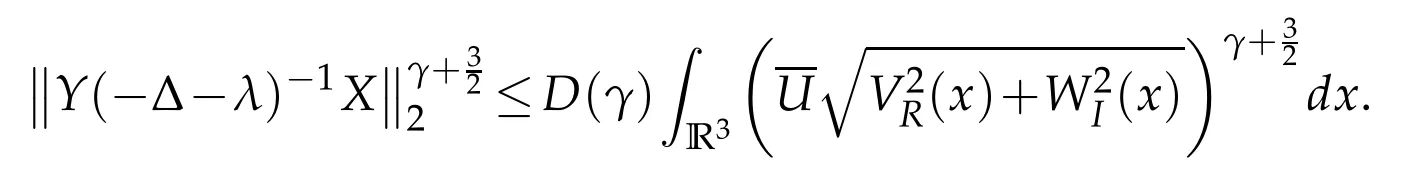
After[20]we know that

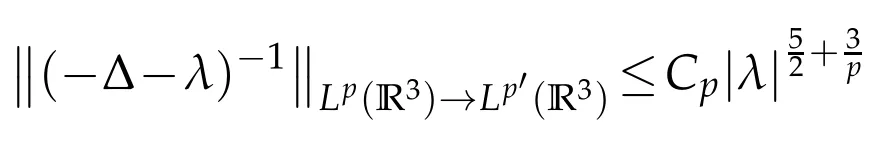
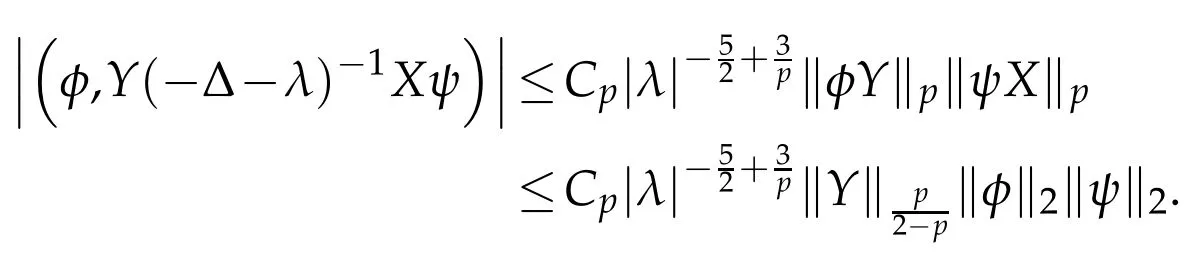
Lemma 2.2.Suppose that Conditions 1 and 3 are satisfied.The discrete spectrumσd(H)of H(ρ)has no point on the open positive semi-axis.

Proof.Putting after Kato[18]

and observing that after Conditions 1 and 3

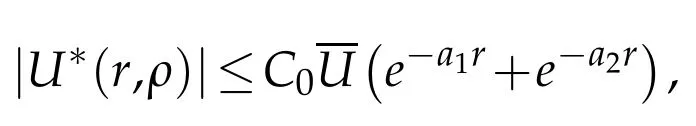
Following Stepin[47]we can now improve the bound on the radius of the disc containing the eigenvalues and consequently we can show that the number of eigenvalues of H(ρ)is finite.

Proposition 2.2.Suppose that U(ρ)satisfies Conditions 1 and 3 and that h is the function defined in Lemma 2.1.The following properties hold

(i)The discrete spectrum of H(ρ)is located in the disc D(0,R)where

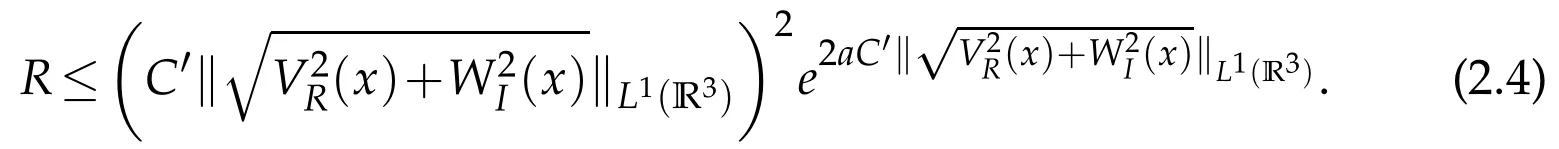
(ii)The number N(H)of eigenvalues of H(ρ)is finite in D(0,R).

Set for 0＜α＜a

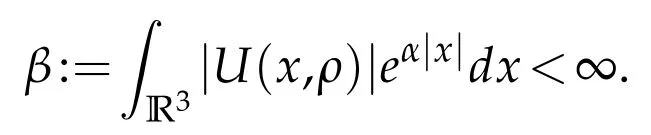
Then for any

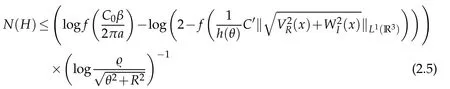
Proof.

(i)Due to Lemma 2.2 the discrete spectrumσd(H)of H(ρ)which we know not to have any eigenvalue on the open positive semi-axis cannot include 0.So in factσd(H)⊂D(0,Λ)has no accumulation point,and therefore is finite.

(ii)After Lemma 2.1 the operatoris Hilbert-Schmidt then its“square”is of trace class.Therefore after Conditions 1 and 3,the Fredholm determinant

whereΓ(x,y;ζ)is defined in Lemma 2.1,has an analytic continuation from C+to the stripand in Sa,one has

DefiningΦ(z)=D(z+iθ),choosingand applying Jensen’s Theorem[43]to the analytic functionΦ(z)we get

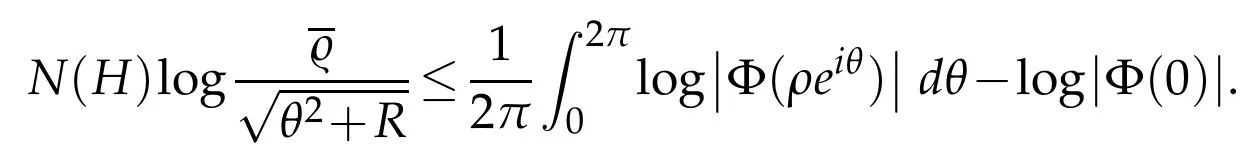
After Hadamard’s inequality(see[38,p.175])we have the bound

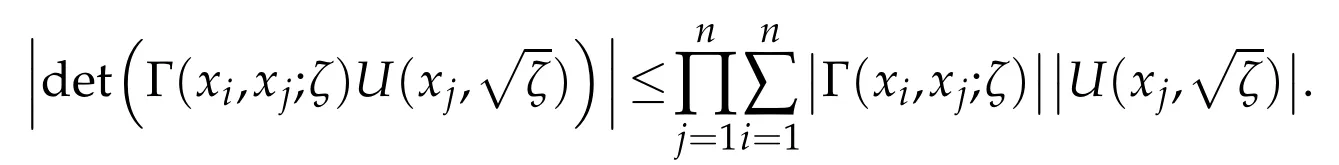
As

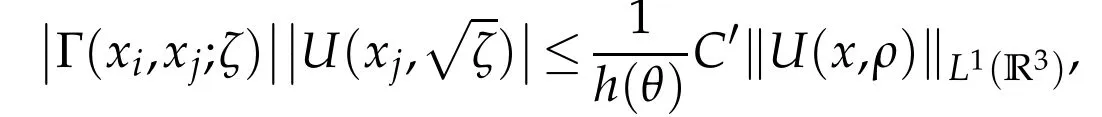
we see that

Moreover,as we also observe that

we get exactly the required estimate(2.5).

Remark 2.1.Considering the case where U0≡0 and the potential U is independent of energy and assuming that U=V+iW is replaced by V+igW,where g＞0 is a(small)coupling constant and W＜0,then under less restrictive assumptions on the decay of U(possibly long-range),Wang shows[49,50]a quasi-optimal result:defining H(g):=-Δ+V+igW,then for g small enough

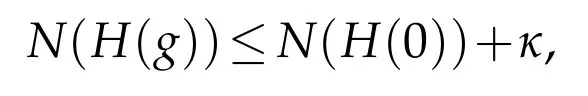
whereκ=0(resp.κ=1)if 0 is(resp.is not)a resonance of H(0).

We conjecture that this result is likely to hold also for an energy dependent Hamiltonian satisfying Conditions 1 and 3.

3 A priori estimates,spectral singularities and limiting absorption principle for H(ρ)

Let C+be the positive half-plane C+:={ρ∈C*:ℑm(ρ)≥0},and C′+the corresponding open half-plane C′+:={z∈C:ℑm(z)＞0}and denote by MKthe set MK:={ρ∈C+:|ρ|≥K}for a K＞0.

We introduce for p∈R and any measurableΩ⊂R3the weighted spaces

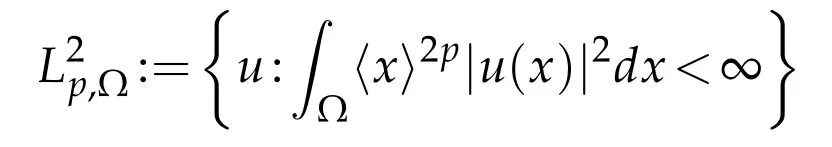
with inner product

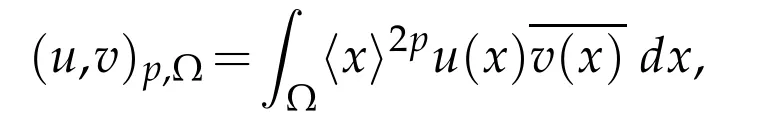
and domain

Denote by D the operator

After Saito[46]we define the spectral singularities of H.

Definition 3.1.We say thatρ∈C is a spectral singularity of H(ρ)if the homogeneous equation

with“radiation condition”(see Ikebe and Saito[16])

In fact,in the self-adjoint case(when U is real),Ikebe and Saito proved[16]that for any pair(ρ,f)∈with K={ρ∈C|0＜a＜b＜∞,0＜α＜∞},the problem(3.4)-(3.5)has a unique solution.Then Saito[46]showed that this result also holds in the complex case provided K∩Σ=∅and we wish to extend this to the complex and energy-dependent case.

3.1 A priori estimates

Extending to the energy dependent case the strategy of Saito in[46],we have first

Lemma 3.1.The two following properties hold

(ii)Letγ,β∈R withγ≤βand suppose thatℑmρ＞0.Let u∈such that∂ju∈for j=1,2,3 and(H(ρ)-ρ2)u∈.Then u∈withα=min{γ+,β}.

Proof.

(i)Let u be a solution of(H(ρ)-ρ2)u=f.Multiplying the two sides by〈x〉2γ,integrating by parts on the shell Br0,r:={x:r0≤|x|≤r}with boundary∂Br0,r=Sr∪Sr0(with Sr={x:|x|=r})and taking real parts,we have

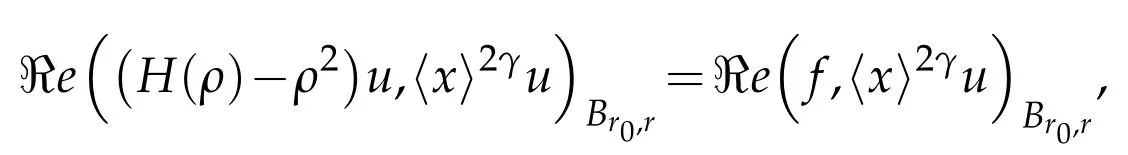
which rewrites

whereρ1=ℜe(ρ)andρ2=ℑm(ρ).After radiation condition we see that the surface term on Srvanishes for large r so,using Cauchy-Schwarz inequality we get

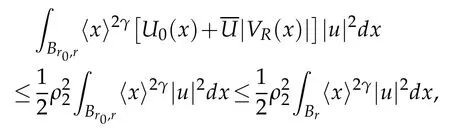
and letting r go to infinity we conclude from hypotheses that.(ii)Suppose first thatρ1=ℜe(ρ)/=0.In the same stroke as in(i)we have

which rewrites

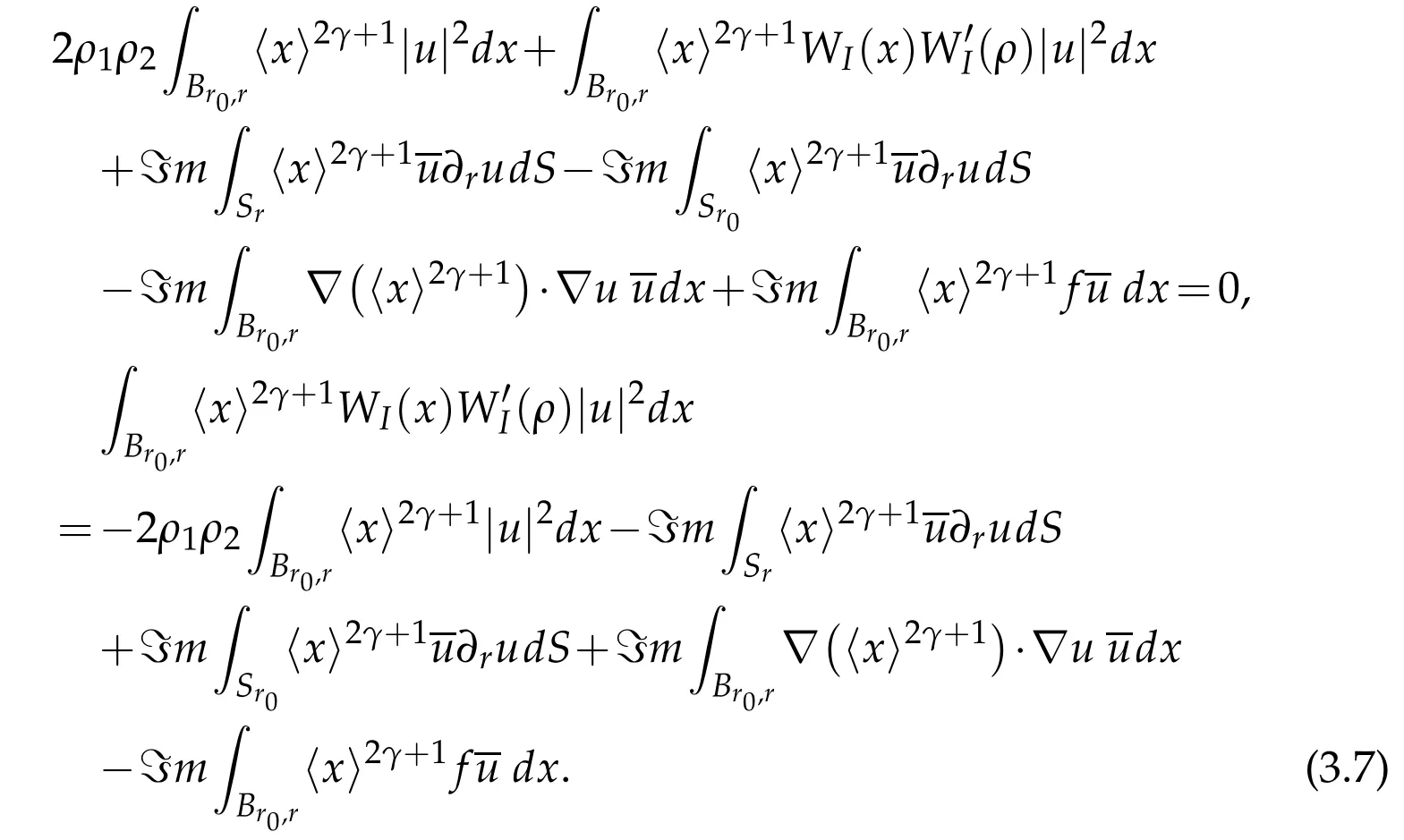
Moreover using the previous argument,namely that due to decay properties of WI,we have for a suitable r0and any r＞r0

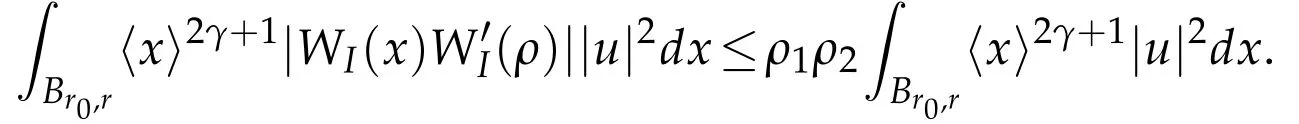
Thus

From(3.7)and(3.8)it is therefore deduced that

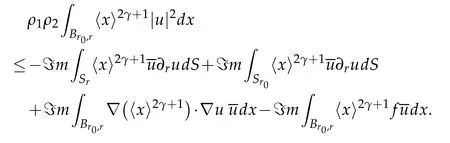
As in(i)we see that

and becauseρ1/=0 we get finally u∈withα=min{γ+,β}.

Suppose now thatρ1=0.Going back to(3.6)we get

Then observing that

and taking r0such that＜ρ2,we get

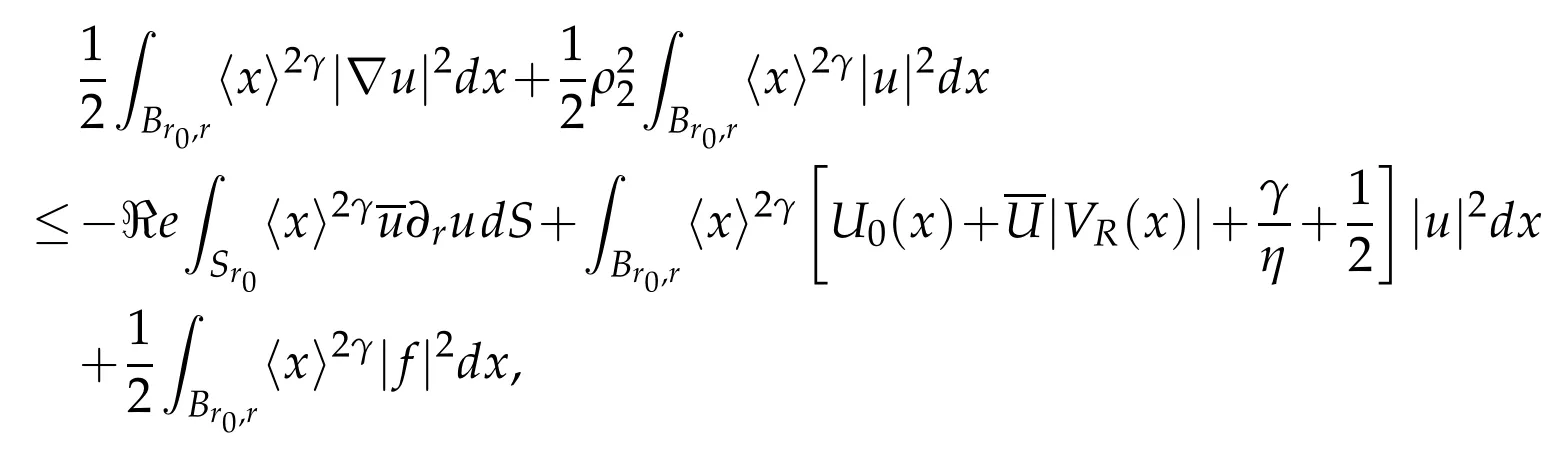
and letting r go to infinity we still conclude that u∈.

Proposition 3.1.(i)Letρ∈C+withℑmρ＞0 and let u∈Dρ,s.Then u,∂ju∈for j=1,2,3.

(ii)Forρ∈C+withℑmρ＞0 and let u∈Dρ,sthe following estimate holds

where the positive constant C=C(ρ)is bounded on any compact of C+.

(iii)For anyρ=ρ1+iρ2∈MKwith K＞0 and any u∈Dρ,s,one has

Proof.

(i)Property(i)is a consequence of Lemma 3.1.

(ii)Taking the real and imaginary parts of

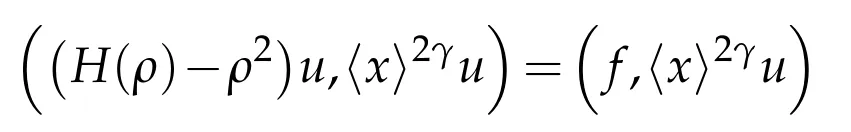
withγ≤s we get

where as beforeρ1=ℜe(ρ)andρ2=ℑm(ρ).

From(3.11)and Condition 2 we deduce that

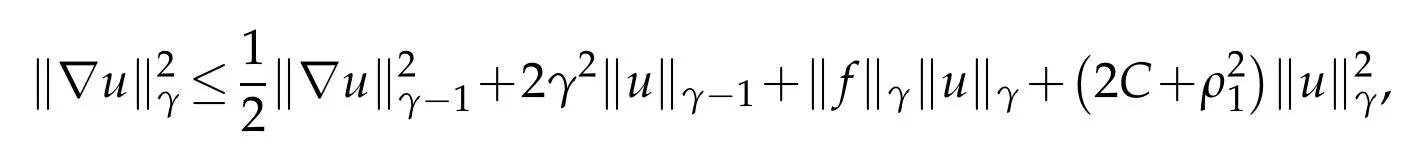
where C is the positive constant in Condition 2,which gives

where we observed that|U(x,ρ)|≤C〈x〉-2s.

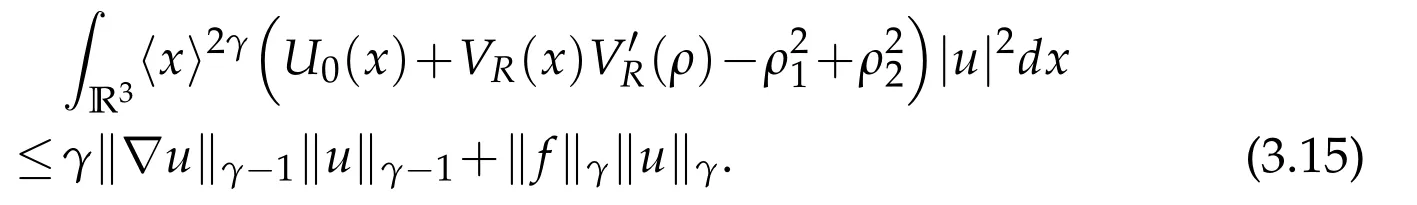
We estimate the left-hand side as follows.After Condition 2 we can find a positive number R=R(ρ2)such that

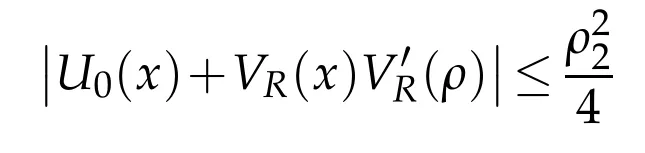
for|x|≥R.Then we get

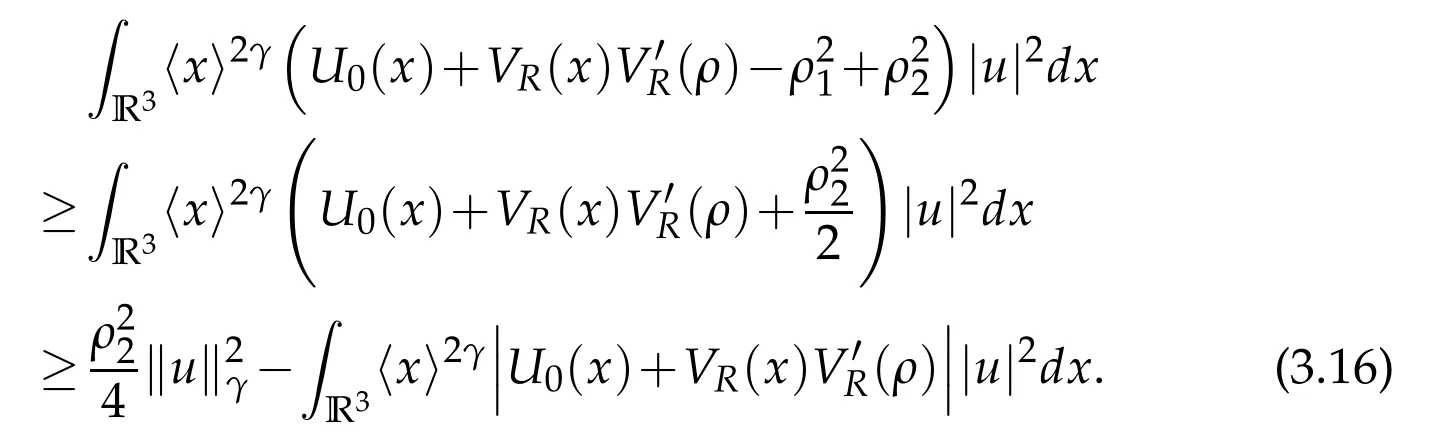
Using the inequality

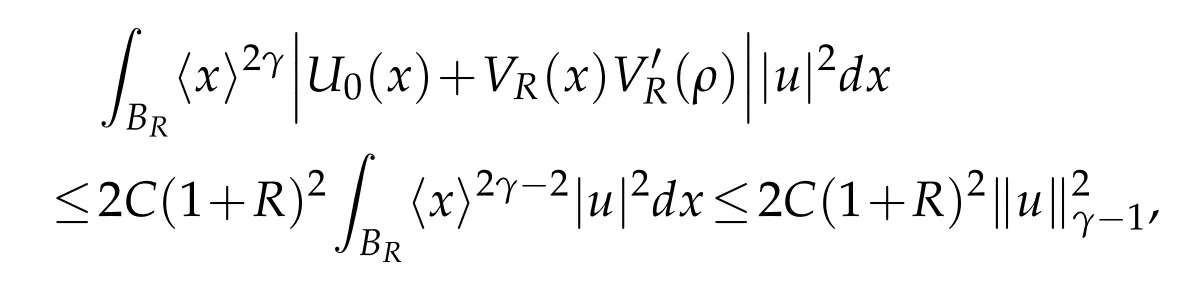
together with estimates(3.15)and(3.16),we obtain

and using(3.14)and(3.16)we end with

Takingγ=s in(3.18)andγ=s-1 in(3.13)we get

In the same stroke,takingγ=s-1 in(3.18)andγ=s-2 in(3.13)we get

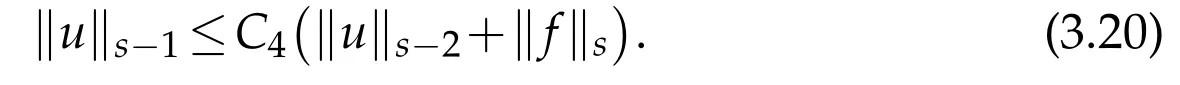
(iii)From(3.12)and using the radial coordinate|x|=r withwe see that

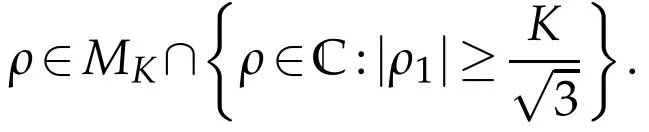
Suppose now that

Denote by Drthe operatorwhere D is defined by(3.3).

Proposition 3.2.Let K＞0.There is a positive constant C such that forρ∈MKand u∈Dρ,s,the following estimate holds

where u is a solution of(H(ρ)-ρ2)u=f.

Proof.Letφbe a continuous piecewise differentiable function on(0,∞).Observing that equation(H(ρ)-ρ2)u=f rewrites

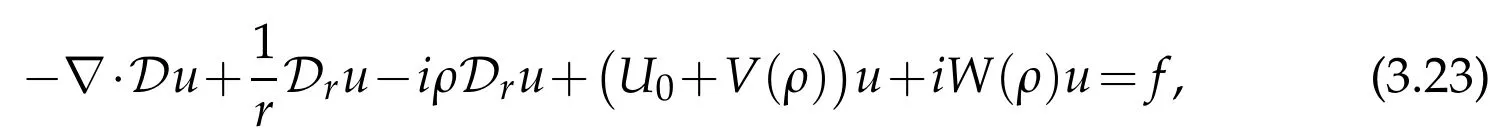
where V(ρ):=ℜe(U(ρ))and W(ρ):=ℑm(U(ρ))forρ∈C+.

Let us estimate the right hand side.Using the identity

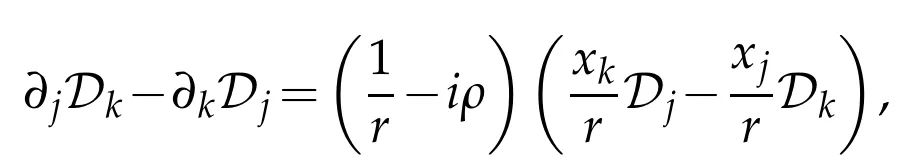
we get first

Then

Integrating by parts in the first integral of the right hand side gives

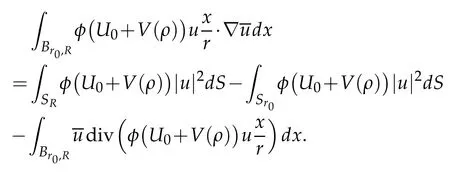
The last right contribution is

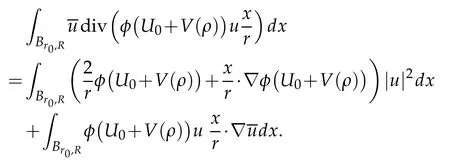
Then we obtain

Observing that

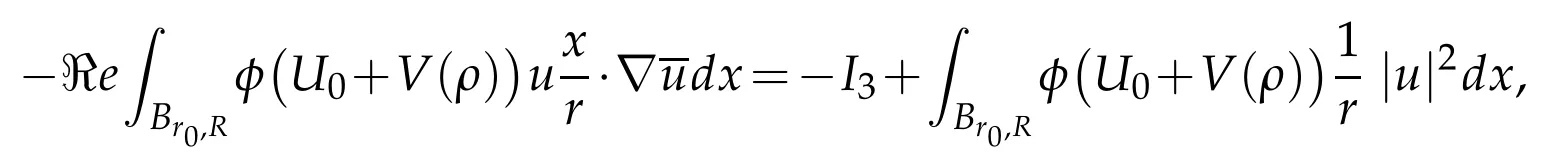
we get finally

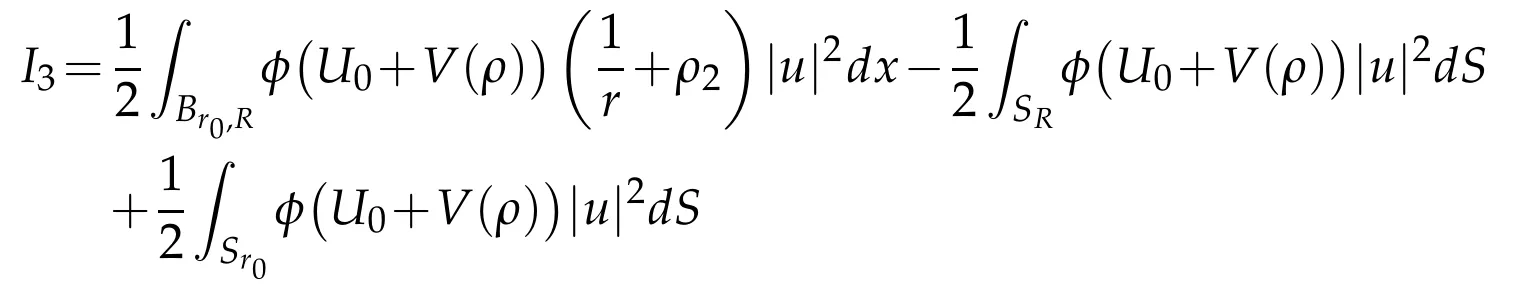
In the same stroke

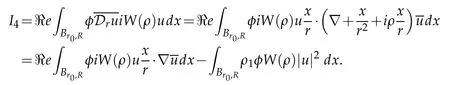
Integrating by parts in the first integral of the right hand side gives

The last right contribution is

Then we obtain

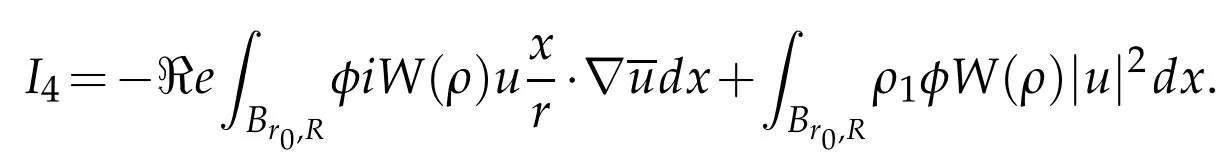
Observing that

we get finally

Plugging(3.25)-(3.28)into(3.24)we get the identity

Choosingφ(r)=r for 0≤r≤1 andφ(r)=22s-1〈r〉1-sfor r＞1 and plugging in(3.29)we get

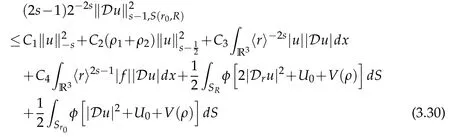
for positive constants C1,2,3,4,where we used Conditions 2 and 3.

Recalling that Du∈L2,u∈L2andone observes that the two surface integral in the right hand side vanish respectively when r0→0 and R→∞so we can pass to the limits r0→0 and R→∞in(3.30)and we find

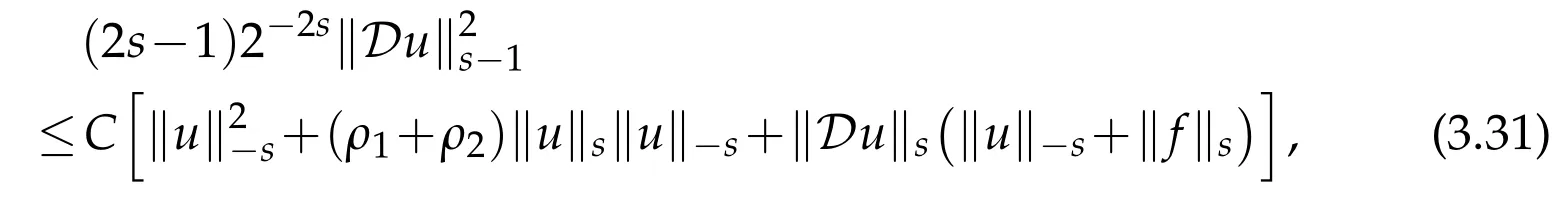
which gives(3.22)after using Proposition 3.1.

Proposition 3.3.Let K＞0 andρ∈MKand denote by ERthe exterior of the ball B(0,R)in R3for a R＞0.For u∈Dρ,ssolution of(H(ρ)-ρ2)u=f,the following estimate holds

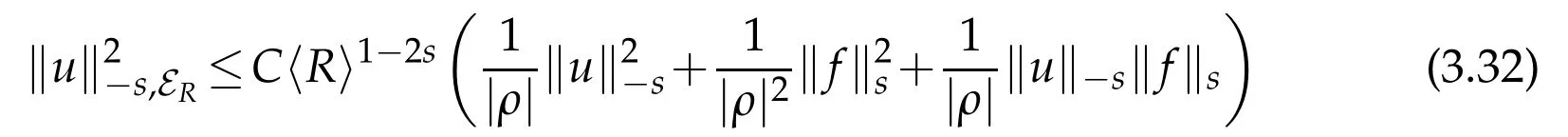
for any R＞0,where C is a positive constant independent of R.

Proof.Let r1and r2be two positive numbers such that MK⊂A1∪A2with

Suppose first thatρ∈R1.We have

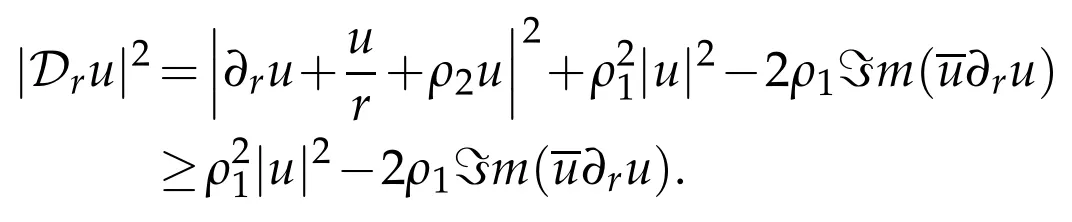
Then integrating on the sphere Srwe get

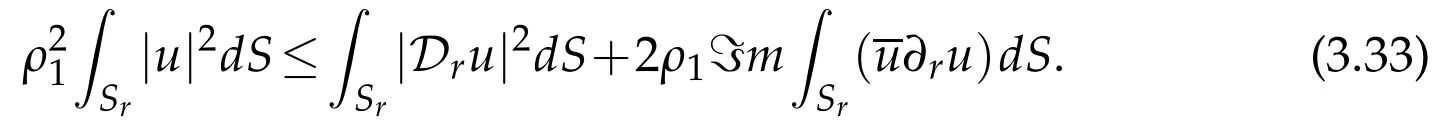
Integrating identity(H(ρ)-ρ2)on the ball Brand taking imaginary part we find

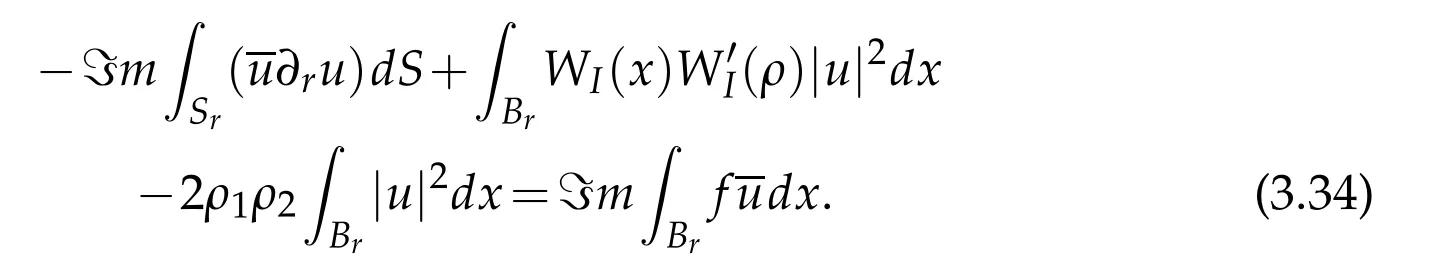
Combining(3.33)and(3.34)we get

Multiplying both sides of(3.35)by〈r〉-2sand integrating from R to∞,we obtain

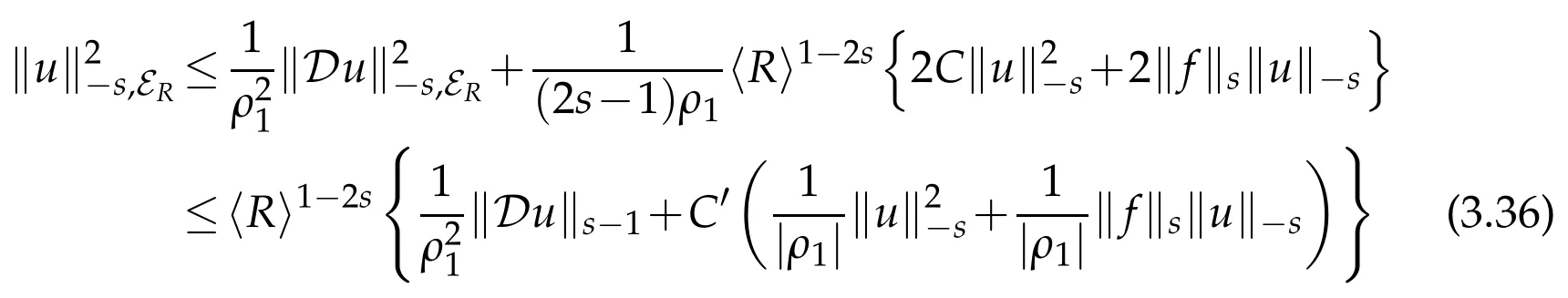
for a positive constant C′.

From(3.36)and Proposition 3.2,we get(3.32)withρinstead of ρ1.

As ρ ∈ R1we see thatthen finally(3.32)holds in R1.Suppose now thatρ∈R2.Using the identity

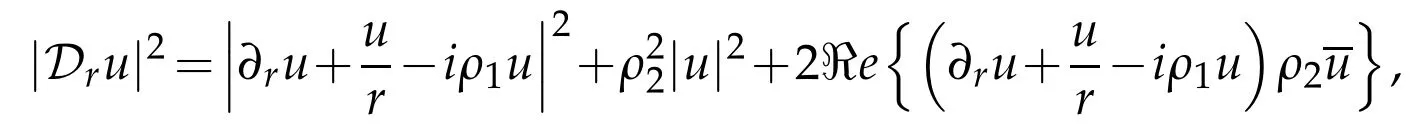
we have

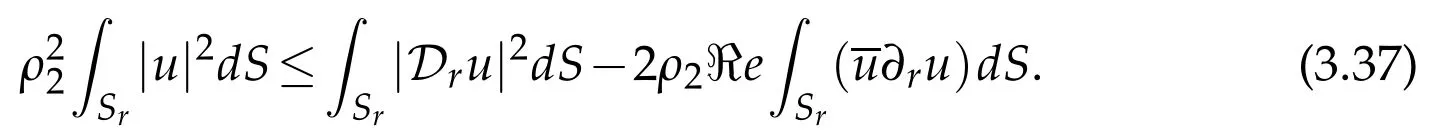
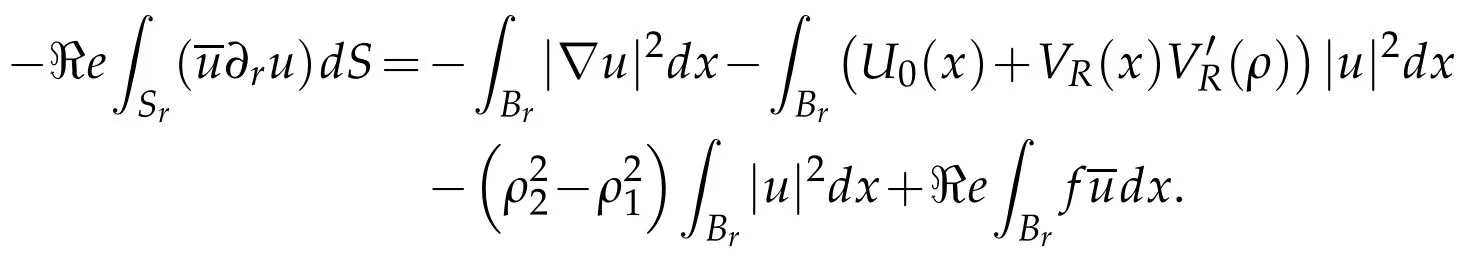
Then

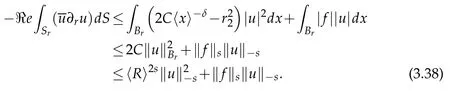
Then in the same way as in the first case we get(3.32)withρreplaced byρ2.As nowρ∈R2we see that|ρ|≤2|ρ2|then finally(3.32)also holds in R2which ends the proof.

Proposition 3.4.Let K＞0 and assume that M⊂MKis an open subset of MK,with.Letρ∈MKand u∈Dρ,ssolution of(H(ρ)-ρ2)u=f.The following estimates hold

for any R≥0,where C is a positive constant independent of R,

Proof.Recall that H0=-Δ+U0is the energy independent part of H(ρ)=H0+U(ρ).As estimate(3.39)and estimate(3.40)follow after Propositions 3.2 and 3.3,we have just to show(3.41).Supposing the contrary,we can find sequences{ρn}in M and{un}in Dρn,swith

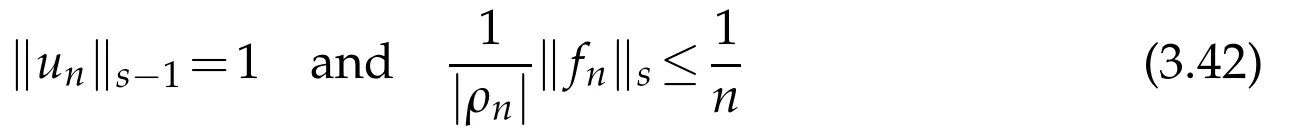
a)Suppose first that the sequence{ρn}is bounded in M.After the standard interior estimate for(H0+U(ρ)-ρ2)u=f we have for any

for 0＜r＜R andρ∈K where K is a bounded subset of C+.After(3.43){un}is relatively compact inso

But using once more(3.43)we see that un→u inFrom(3.42)we have:‖fn‖s→0.This implies,using(3.44),that u weakly solves(H0+U(ρ)-ρ2)u=f but as u∈it is also a strong solution of (H0+U(ρ)-ρ2)u=f.Applying Proposition 3.3 we get

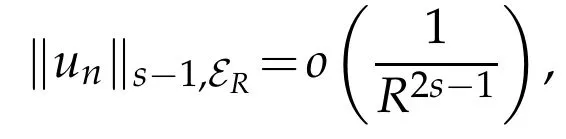
then un→u inand‖u‖s-1=1.Now after Proposition 3.2‖Dun‖s-1,E1≤C

and as un→u inH1locwe find that

So we deduce that(H0+U(ρ)-ρ2)u=f and then u=0 sinceρ/∈Σ,which contradicts‖u‖s-1=1.

b)Suppose now that the sequence{ρn}is unbounded in M.Then after Proposition 3.3 with R=0 and hypotheses(3.42)we have

which still contradicts‖u‖s-1=1.

3.2 Essential spectrum and spectral singularities

Recall that a point ofΣis called a spectral singularity of H(ρ)and let us denote byΣ′the setΣ′=Σ∩C′+and byΣRthe real part ofΣ:ΣR:=Σ∩R.

Lemma 3.2.Let H(ρ)be defined by(1.1)with U0and U(ρ)satisfying Conditions 2 and 3.The following properties hold

(i)

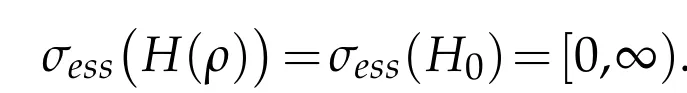
(ii)

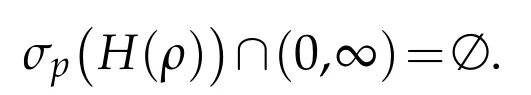
(iii)The pointρbelongs toΣ′if and only ifρ∈C+andρ2∈σp(H(ρ)).

(iv)Σ′is a discrete set.

Proof.

(i)Interior estimate for solutions of equation H(ρ)u-ρ2u=f reads

for 0＜s＜r andℑm(ρ)＞0,thus using decay Condition 2 of U0and U(ρ)at infinity,we see that U0and U(ρ)areΔ-compact,which proves that

(ii)This point is a direct consequence of Lemma 2.2.

(iii)Letρ∈Σ′and let u be a solution of(3.4)-(3.5).After Proposition 3.1 and(3.1)we see that u is actually an eigenfunction of H(ρ)associated to the eigenvalueρ2.Inversely if u is an eigenfunction of H(ρ)withρ∈C+associated to the eigenvalueρ2,u is a non-trivial solution of(3.4)-(3.5).

(iv)This point is a direct consequence of steps(iii)and(i).

For anyρ∈C+we can define the operator T(ρ)by

Moreover one observes that T(ρ)is compact forρ∈C+and therefore thatσ(T(ρ))is a discrete subset of C*.

From the previous informations one gets

Lemma 3.3.The following properties hold

(i)The pointρ∈C+belongs toΣif and only if 1∈σ(T(ρ)).

(ii)ρ∈C+Σ′if and only ifρ∈C+and ifρ2∈ϱ(H(ρ))(the resolvent set of H).

(iii)Σis a bounded subset of C+.

(v)ΣRhas zero Lebesgue measure in R.

Proof.

(i)Suppose thatρ∈Σ.If u satisfies(3.4)and(3.5)we have

(ii)Letρ∈C+Σ′.After step(iv)of Lemma 3.2,we can find a sequenceρn∈C+such thatandρn→ρ.Suppose thatAs the resolventis well defined and I-T(ρn)is invertible after step(i),we can defineby

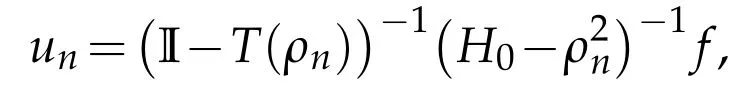
Applying Proposition 3.1,we can extract a subsequence still denoted by unsuch that un→u inwhere u solves(H(ρ)-ρ2)u=f.Observing that u∈D(ρ,s)we get that u∈D0after Proposition 3.1.Then f=(H(ρ)-ρ2)u∈(H(ρ)-ρ2)D0which shows that

(iii)Suppose that there is a sequenceρn∈Σsuch thatρn→∞for n→∞.For any n we can pick asuch that

Then we can write

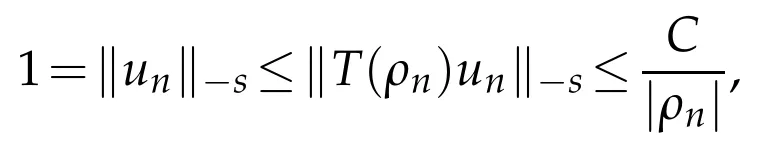
where C does not depend on n.As the right hand side goes to 0 when n→∞we get a contradiction.

(iv)Letρn∈Σ∩such thatwithand consider a solution unof the homogeneous problem(3.4)and(3.5)with‖un‖-s=1.

From step(iv)of Lemma 3.2 we see thatρis real and≥K.Putting M0={ρ=ρ1+iρ2:|ρ1|＞K/2,ρ2＞0},we can assume that ρn,ρ∈.After step(iii)of Lemma 3.2 we see thatthen we can apply step(i)to show that un=T(ρn)un,‖un‖-s=1.

Observing that after Theorem 3.2(replacing fnby-U(ρn)unand H(ρ)by H0)we see that the sequence{T(ρn)un}is relatively compact,then there exists a subsequence still denoted by unsuch that

(v)It follows from a direct application of the technical Lemma 6.2 of Kuroda in[22].

We have now the following theorem.

Theorem 3.1.(i)The essential spectrum of H(ζ)fills the positive half-axis

(ii)One has

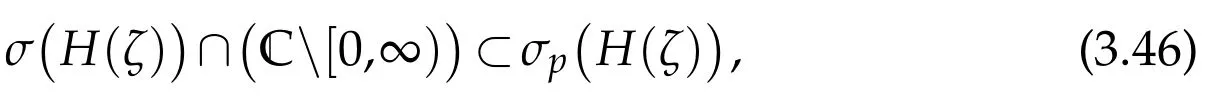
and

The eigenvalues in C[0,∞)have finite multiplicity and form an isolated bounded set without limit point in C[0,∞).

(iii)

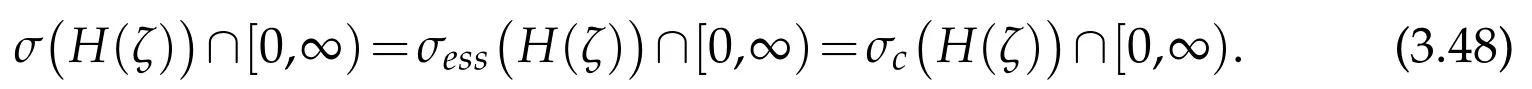
(iv)

Proof.

(i)This follows after(i)in Lemma 3.2.

(ii)As CR+={ρ2:ρ∈C+},we get from Lemma 3.3(step(ii))and Lemma 3.2(step(iii))that CR+=ϱ(H(ρ))∪σp(H(ρ))thereforeσp(H(ρ))⊃σ(H(ρ))∩R+.We obtain thatσp(H(ρ))∩R+=∅by using step(iii)from Lemma 3.2.The remaining properties in(ii)follow by using step(i)from Lemma 3.2.

(iii)A direct consequence of relationσp(H(ρ))∩R+=σr(H(ρ))∩R+=∅.

(iv)We already know thatσp(H(ρ))∩(0,∞)=∅.But C[0,∞)={ρ2:ρ∈C+}so we see that C[0,∞)=ϱ(H(ρ))∪σp(H(ρ))which implies that C[0,∞)∩σ(H(ρ))⊂σp(H(ρ)),and we use step(i)to conclude.

Theorem 3.2.Suppose Condition 2 is satisfied and denote by MKthe set

(i)Σis a bounded subset of C.

limit point in the open half-plane{ρ∈C+:ℑm(ρ)＞0}.

(iii)A pointρbelongs to{ρ∈C+:ℑm(ρ)＞0}if and only ifρ2belongs to the discrete spectrum of H(ρ)andρ2∈ϱ(H(ρ))for anyρ∈C+Σsuch thatℑm(ρ)＞0.

Proof.

(i)A consequence of property(iii)and property(v)in Lemma 3.3.

(ii)Follows after property(iv)in Lemma 3.2 and property(iv)in Lemma 3.3.

(iii)Is obtained by applying property(iii)in Lemma 3.2 and property(ii)in Lemma 3.3.

3.3 Limiting absorption principle

Using the results of Section 3.1,the following result holds

Theorem 3.3.Suppose Condition 2 is satisfied and denote by MKthe set MK:={ρ∈C+:|ρ|≥K}for a K＞0.Assume that M is an open set in C+such that∩Σ=∅and M⊂MK.

(i)There exists a unique solution u(ρ,f)∈of equation(H(ρ)-ρ2)u=f

with

(ii)The solution u(ρ,f)for(ρ,f)∈satisfies the estimates

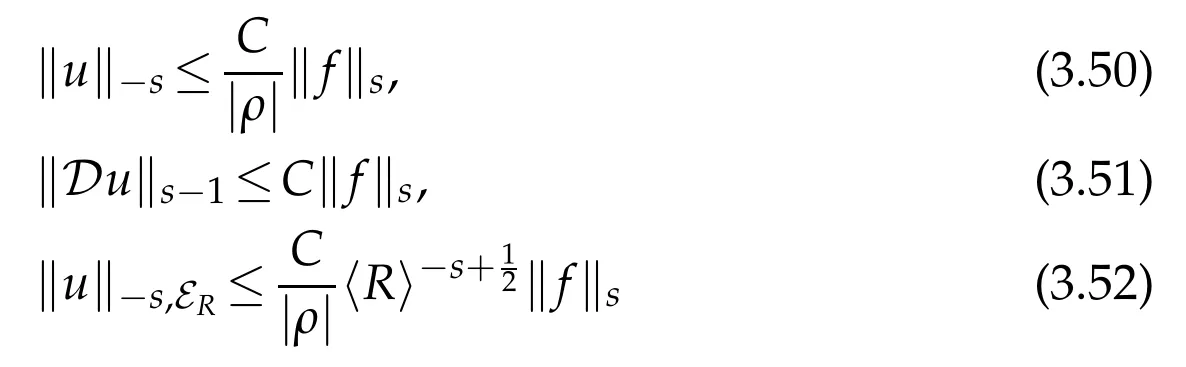
for R≥1.

(iii)The resolvent R(ρ):=(H(ρ)-ρ2)-1is a bounded operator:R(ρ)∈Lfor ρ∈and

(iv)The resolvent R(ρ):=(H(ρ)-ρ2)-1is a compact operator for anyρ∈.

Proof.

(i)Let us firstly suppose that ρ2∈ϱ(H(ρ))for anyρ∈M.Let(ρ,f)∈M×and consider u≡u(ρ,f)=R(ρ2)f.As u∈D0,sand f∈,u is the unique solution of

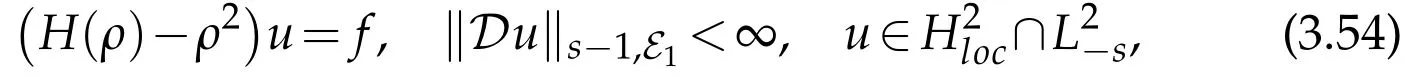
moreover u∈Dρ,s.

(ii)After Proposition 3.4,u satisfies estimates(3.39)-(3.41).Let(ρ,f)∈×and consider a sequence{ρn}of M converging toρand un≡u(ρn,f).From(3.41){un}is bounded inthen it is also a bounded sequence in L2(BR)for any R＞0.Using interior estimate(3.43)we can extract a subsequence{u′n}converging to u inand u is a weak solution of(H(ρ)-ρ2)u=f hence u∈so u is also a strong solution of the same equation.Estimates(3.39)-(3.41)allow us to show that{u′n}converges to u inand that‖Du‖s-1,E1＜∞.Then u is actually a solution of(3.54)satisfying estimates(3.50)-(3.52).Uniqueness follows asρ/∈Σ.

(iii)After(3.50)the resolvent(H(ρ)-ρ2)-1is a bounded linear operator fromtoand(3.53)is satisfied.

(iv)Suppose that(H(ρ)-ρ2)-1is not continuous atρ∈.Then there exist sequencesρn∈and fn∈such that

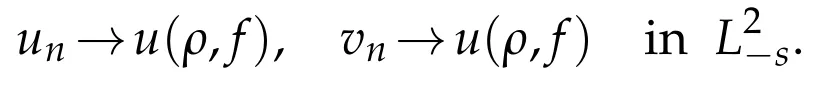
Therefore we get that‖un-vn‖s→0 which contradicts(3.55).

(v)Letρ∈M.It follows from(3.9)of Proposition 3.1 and(3.50)that

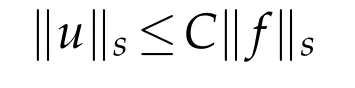
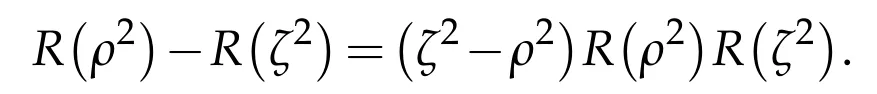
This result implies easily the following Corollary(Limiting Absorption Principle)which is the first part of Theorem 1.1.We omit the proof.

Theorem 3.4.Recall thatΣR:=Σ∩R.Suppose Condition 2 be satisfied and letρ∈RΣR∪{0}.Then for any f∈and any sequence{ρn}satisfying

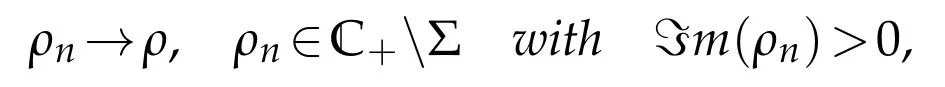
there exists

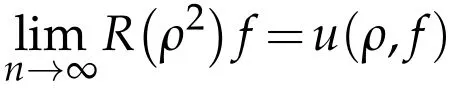
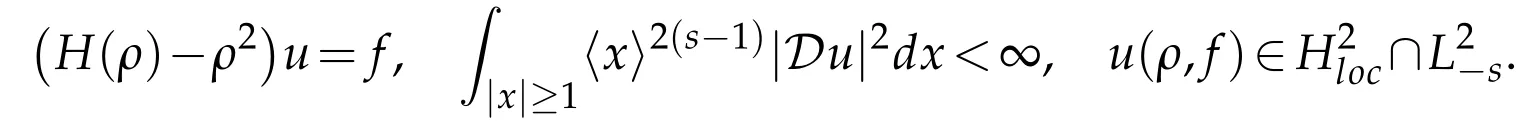
4 The small or dissipative cases

Our aim in this section is to show briefly the three last parts of Theorem 1.1 i.e.that,provided the potential is either small or dissipative with a real part small enough,the Limiting Absorption Principle holds for H(ρ)on any finite interval ofthe whole positiverealaxis.We essentially extendideasof Mochizuki[27].

A fter Theorem 3.1 andLemma 2.2,the resolventwith ρ=is welldefined inmoreover the resolvent formula holds

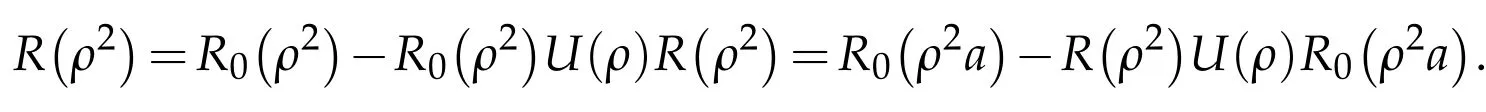
After Lemma 2.1 U(ρ2)R0(ζ)is Hilbert-Schmidt and as R(ρ2)is bounded R(ρ2)U(ρ)R0(ρ2)is also Hilbert-Schmidt,and we have

Proposition 4.1.(i)The kernel R(x,y;ρ2)of R(ρ2)satisfies the equation

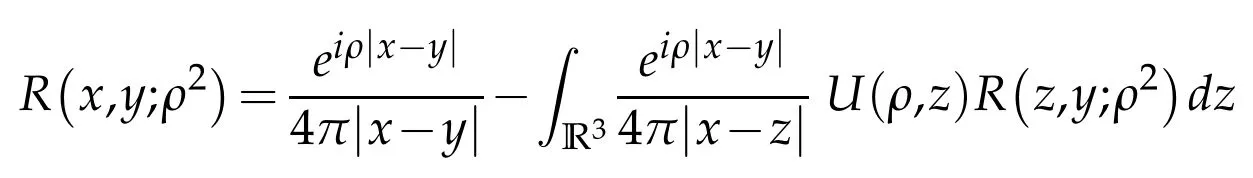
for almost any pair(x,y).Moreover R(x,y;ρ2)is symmetric in x and y.

(iii)The kernel R*(x,y;ρ2)of the operator R*(ρ2):=(H*(ρ)-ρ2I)-1satisfies the equation

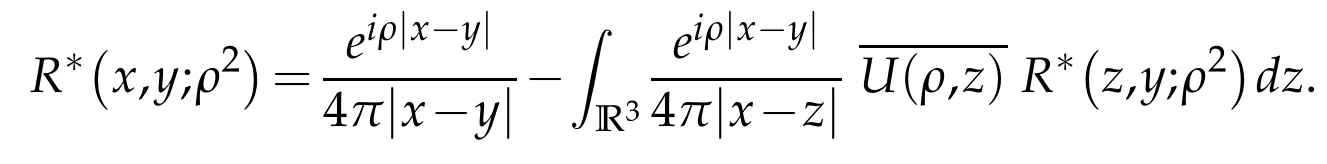
Proof.The proof follows exactly the lines of Mochizuki[27,Theorem 1.2]or Ikebe[15,Theorem 1].

After Condition 2 we see that.Defining the operator A(ρ)(resp.B(ρ))as the multiplication by(resp.

One checks easily that the following result holds with the same proof as that of[27,Lemma 2.1].

Lemma 4.1.Suppose that for anyρ∈ϱ(H(ρ))there exists a bounded operator T(ρ2)satisfying the equation

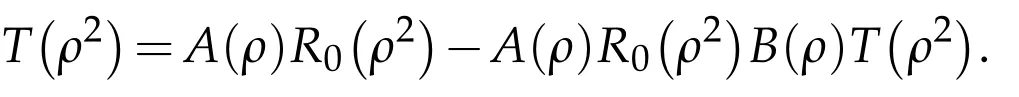
Then T(ρ2)L2(R3)⊂D(B(ρ))and T(ρ2)=A(ρ)R(ρ2).

Let us define the operator Q(ρ)by

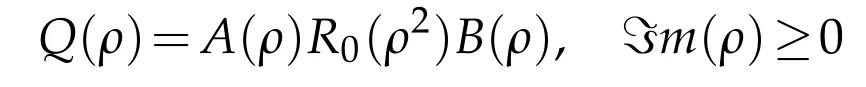
with kernel Q(x,y;ρ)=A(x,ρ)R0(x,y;ρ2)B(y,ρ).

Lemma 4.2.(i)For each fixedρwithℑm(ρ)≥0,Q(ρ)is Hilbert-Schmidt.

Proof.

(i)Using Hardy-Littlewood-Sobolev’s inequality we have

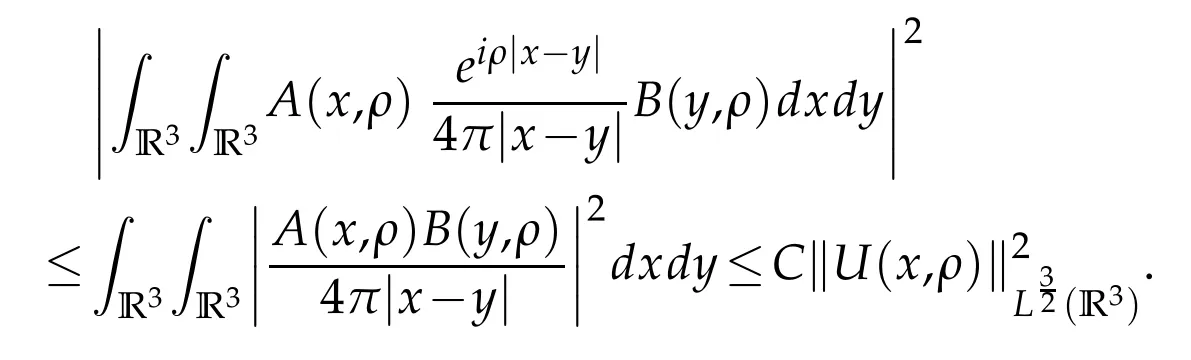
We conclude that Q(ρ)is Hilbert-Schmidt.

(ii)As‖Q(ρ)‖≤C‖Q(0)‖the functionκQ(ρ)is bounded.Moreover

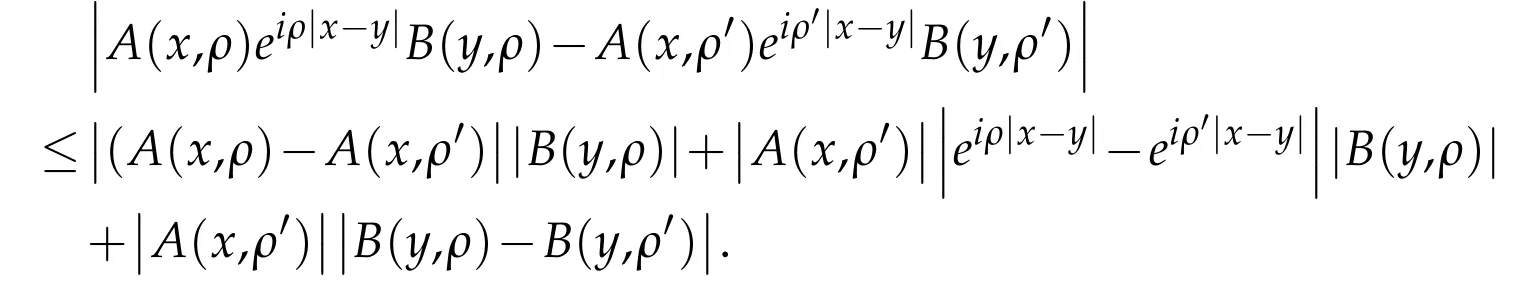
Then choosing R＞0 such that

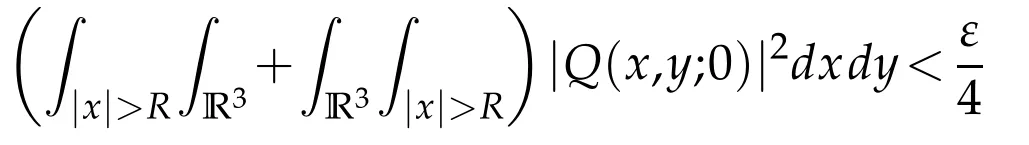
and using the inequalities

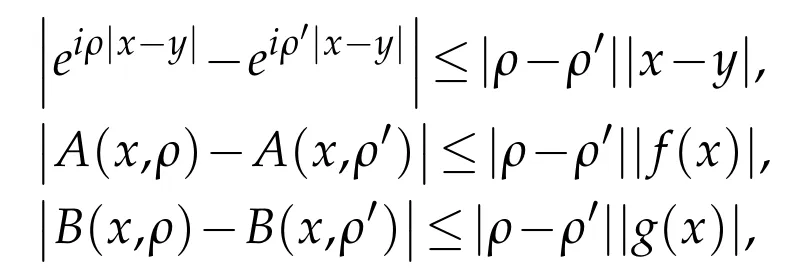
Choosing|ρ-ρ′|small enough,the right hand side is bounded byand we get that‖Q(ρ)-Q(ρ′)‖2≤εwhich proves the continuity ofρ→Q(ρ).

From Lemma 4.1 we have

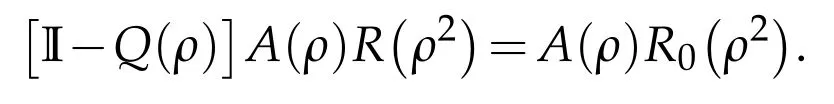
So we see by applying Fredholm’s theory that I-Q(ρ)has a bounded inverse if and only if the equation

has no non-trivial solution in L2(R3).

One checks that points(ii),(iii)or(iv)of Theorem 1.1 follows directly after the proof of the following result.

Lemma 4.3.Under conditions given in points(ii),(iii)or(iv)of Theorem 2.1

Proof.

1.Case(ii)in Theorem 2.1.

After Condition 4 we have

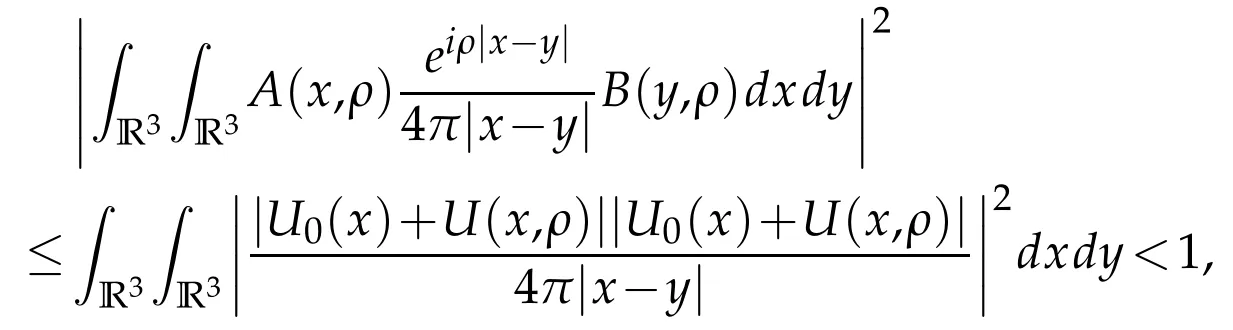
then Q(ρ)is invertible in L2for anyρ∈{ℑm(ρ)≥0}.

2.Case(iii)in Theorem 2.1.

Following Mochizuki[27],we consider A(ρ)and B(ρ)the multiplication operators by A(x,ρ):=|W(x,ρ)|12 and B(x,ρ):=U0(x)+V(x,ρ).We have U(x,ρ)=B(x,ρ)-iA2(x,ρ).Suppose first thatρ=ρ1+iρ2withρ2＞0 and that the equation

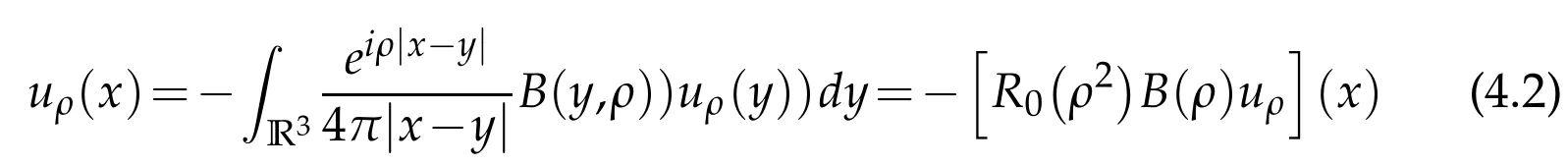
has a non-trivial solution uρ∈L2.Multiplying by U(x,ρ)uρ(x)and integrating,we get

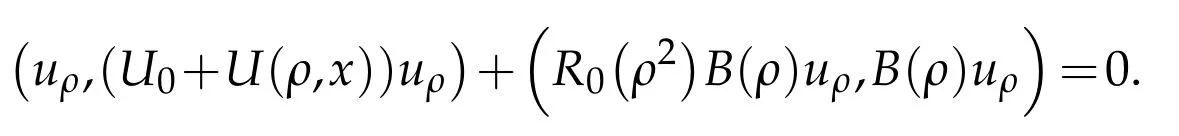
Taking the imaginary parts and denoting byρ=ρ1+iρ2,we get

where E0,λis the resolution of identity associated to-Δ.Then we see that A(ρ)uρ≡0.As-Δ+B(ρ)is self-adjoint this implies that uρ≡0.When ρ2=0,non-trivial solutions of(4.2)are no more in L2but from radiation condition(1.16)we see that A(ρ)uρ∈L2.

So we get

Then taking principal value in the integral,we get

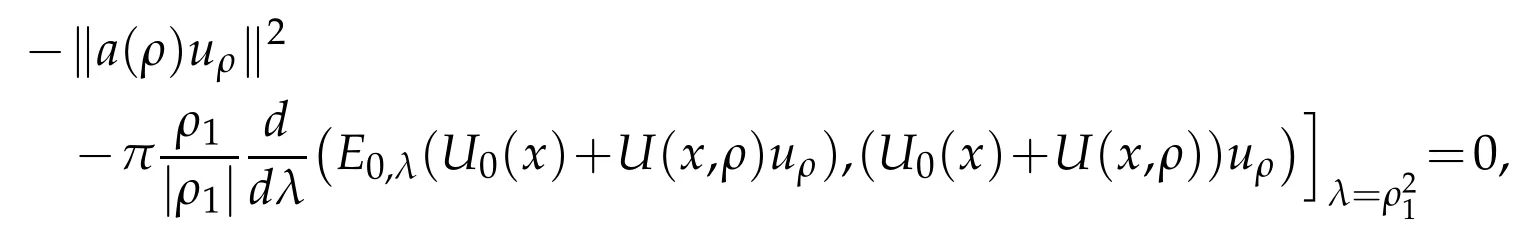
which also implies A(x,ρ)uρ(x)≡0.But as we know after point(1)that the operator Q0(ρ)corresponding to-Δ+U0+U(ρ)has no singular point,we can conclude that uρ(x)≡0.

3.Case(iv)in Theorem 2.1.

which is exactly the semiclassical situation studied by Royer[39,Theorem 1.1].This extends to our energy dependent case.