Weighted and Maximally Hypoelliptic Estimates for the Fokker-Planck Operator with Electromagnetic Fields
2021-05-13WeiXiLiandJuanZeng
Wei-Xi Liand Juan Zeng
1 School of Mathematics and Statistics,and Hubei Key Laboratory of Computational Science,Wuhan University,Wuhan 430072,China.
2 School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China.
Abstract.We consider a Fokker-Planck operator with electric potential and electromagnetic fields.We establish the sharp weighted and subelliptic estimates,involving the control of the derivatives of electric potential and electromagnetic fields.Our proof relies on a localization argument as well as a careful calculation on commutators.
Key words:Maximal estimate,global hypoellipticity,Fokker-Planck operator.
1 Introduction and main results
There have been several works on the Fokker-Planck operator with electric potential V(x)which is

where x denotes the space variable and y denotes the velocity variable,and V(x)is a potential defined in the whole spaceIt is a degenerate operator with the absence of diffusion in x variable,and can be seen as a Kolmogorov-type operator.The classical hypoelliptic techniques and their global counterparts have been developed recently to establish global estimates and to investigate the short and long time behavior and the spectral properties for Fokker-Plack operator K in(1.1).We refer to Helffer-Nier’s notes[4]for the comprehensive argument on this topic,seeing also the earlier work[6]of H´erau-Nier.In the first author’s work[11,12]we improved the previous result and gave a new criterion involving the microlocal property of potential V.Here we also mention the very recent progress made by Ben Said-Nier-Viola[2]and Ben Said[1].Finally as a result of the global estimates it enables to answer partially a conjecture stated by Helffer-Nier[4]which says Fokker-Planck operator K has a compact resolvent if and only if Witten Laplacian has a compact resolvent.The necessity part is well-known and the reverse implication still remains open with some partial answers;in fact various hypoelliptic techniques,such as Kohn’method and nilpotent approach(e.g.,[5,9,14]),were developed to establish the resolvent criteria for these two different type operators(see[4,11-13]).
Inspired by the recent work of Helffer-Karaki[3],we consider here a more general Fokker-Planck operator with electromagnetic fields besides the electric potential,which reads

where n=2 or 3 and H(x)is a scalar function of x for n=2 and a vector field(H1(x),H2(x),H3(x))of only x-variable for n=3,and y∧∂yis defined by

The operator is initiated by Helffer-Karaki[3],where they established the maximal estimate by virtue of nilpotent approach,giving a criteria for the compactness of the resolvent.Here we aim to give another proof,basing on a localization argument and a careful calculation on commutators.Note the operator P in(1.2)is reduced to the operator K given(1.1)for H0;meanwhile the maximal estimates for the Fokker-Planck operator with pure electromagnetic fields(i.e.,V0)was investigated by Zeinab Karaki[8].
Before stating our main result we first introduce some notations used throughout the paper.We will use‖·‖L2to denote the norm of the complex Hilbert space L2(R2n),and denote by(R2n)the set of smooth compactly supported functions.Denote by Fxthe(partial)Fourier transform with respect to x and byξthe Fourier dual variable of x.Throughout the paper we use the notation〈·〉=(1+|·|2)1/2and let〈Dx〉r=(1-Δx)r/2be the Fourier multiplier with symbol〈ξ〉r,that is,

Similarly we can define〈Dy〉.
Theorem 1.1.Let V(x)∈C2(Rn)with n=2 or 3 be a real-valued function and let H(x)be a continuous real vector-valued function.Suppose there exists a constant C0such that for any x∈Rnwe have

and
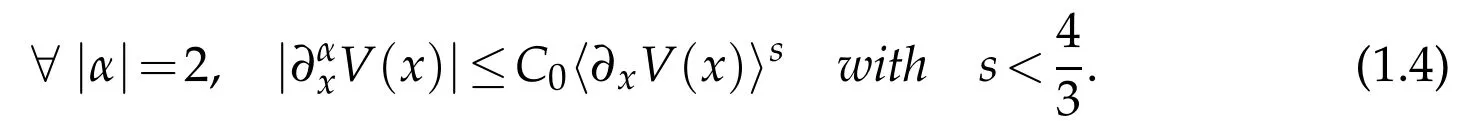
Then we can find a constant C,depending on the above C0and s,such that

Moreover if H satisfies additionally that H∈C1(Rn)and
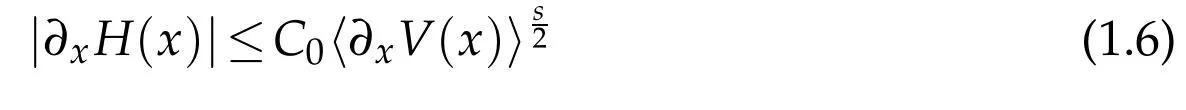
with s given in(1.4),then we have following subelliptic estimate

where

Note if the number s in(1.4)is less than or equal tothen we obtain the sharp subelliptic exponentτ=.This enables to obtain the maximal estimate stated as below(see Section 4).
Corollary 1.1.If V satisfies(1.4)with s≤,and H satisfies the conditions(1.3)and(1.6).Then we have the following maximal estimate,for any u∈(R2n),
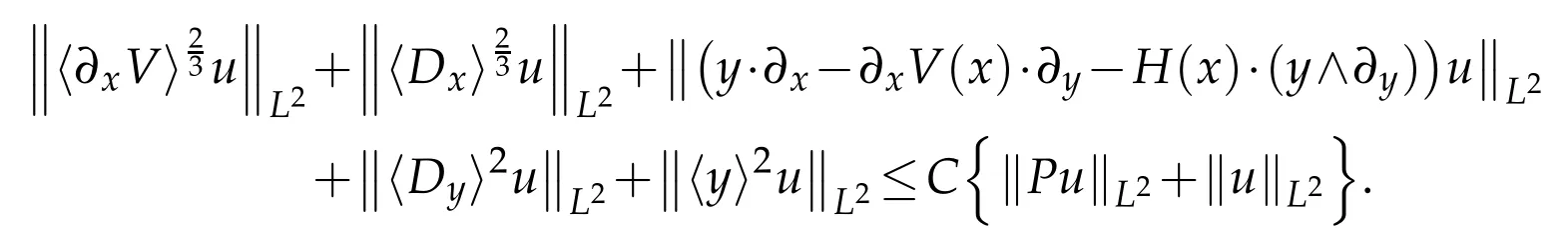
Remark 1.1.The above maximal estimate was established by Helffer-Karaki[3]under similar conditions as that in(1.3),(1.4)and(1.6),but therein they require δ=0 and s<.The result in Theorem 1.1 generalizes the one established by the first author[11],considered therein is a specific case of H≡0.
Another consequence of Theorem 1.1 is to analyze the compact criteria for resolvent of Fokker-Planck operator P in(1.2).Due to the weighted estimate(1.4)we see the Fokker-Planck operator P admits a compact resolve if|∂xV(x)|→+∞as|x|→+∞.Moreover as in the purely electric case(i.e.,H≡0),P is closed linked with Witten Laplace operatordefined by
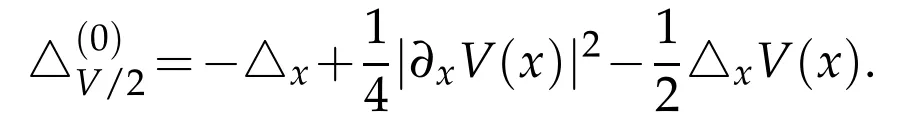
In fact we can repeat the argument for proving[11,Corollary 1.3]to conclude the following
Corollary 1.2.Let H(x)and V(x)satisfy the conditions(1.3),(1.4)and(1.6).Then the Fokker-Planck operator P in(1.2)has a compact resolvent if the Witten Laplacianhas a compact resolvent.
The paper is organized as follow.In Sections 2 and 3 we prove,respectively,the weighted estimate and the subelliptic estimate in Theorem 1.1.The last section is devoted to proving Corollary 1.1,the maximal estimate.
2 Weighted estimate
In this part we prove the weighted estimate(1.5)in Theorem 1.1.From now on we use the notation Q=y·∂x-∂xV(x)·∂y-H(x)·(y∧∂y)and Lj=∂yj+,j=1,...,n.Then we can rewrite the Fokker-Planck operator P in(1.2)as

By direct verification the following estimates

and

Lemma 2.1.Let H and V satisfy(1.3)and(1.4)respectively.Then for anyε>0 we can find a constant Cεsuch that the estimate

Proof.We use(2.2)to get
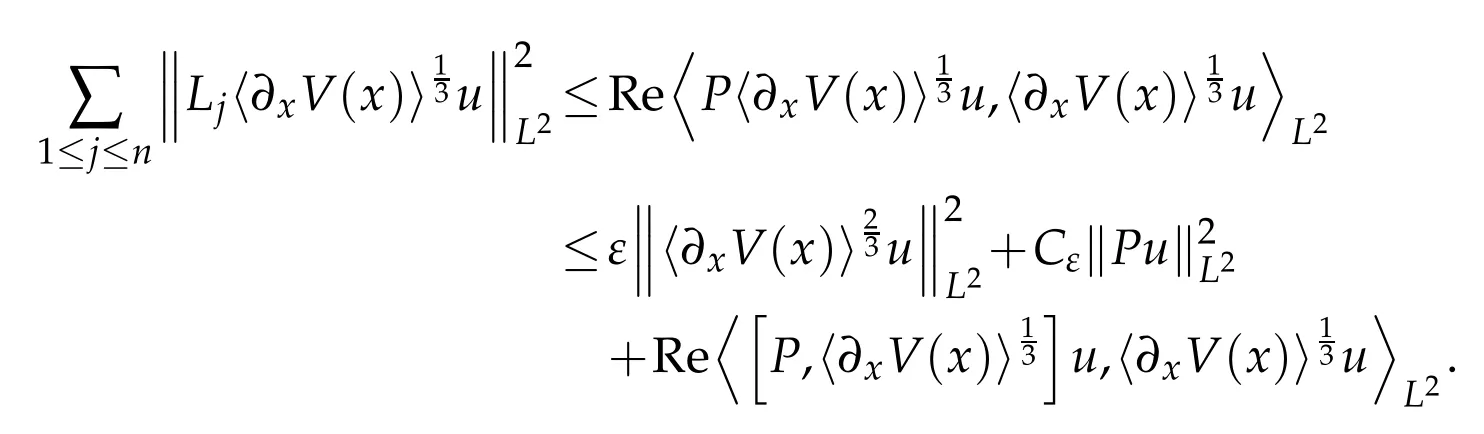
Moreover,it follows from that for anyε1,ε>0 one has

where we used(2.3)and the fact that s<.Combining the above estimates we obtain

Similarly,using again(2.2)and(2.3),

withε1>0 arbitrarily small.Moreover,it follows from the assumption(1.3)that for anyε,ε1>0
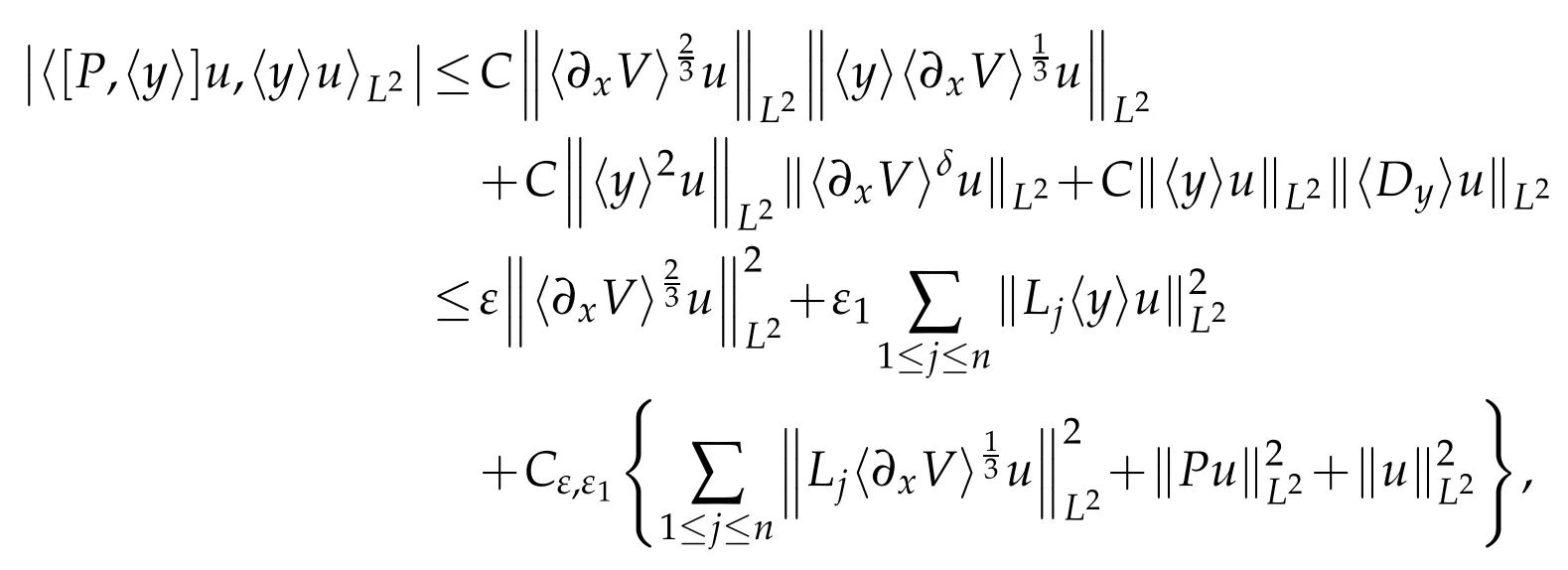
where the last inequality holds because of(2.3)and the fact thatδ<.As a result combining the above estimates and choosingε1small enough,we conclude
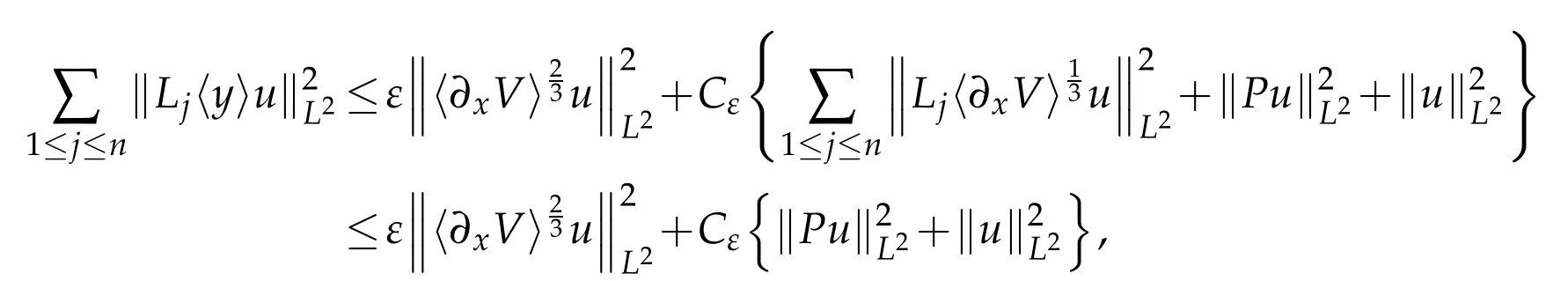
the last inequality using(2.4).This with(2.4)completes the proof of lemma.
Proof of Theorem 1.1:weighted estimate.Here we will prove the weighted estimate(1.5)in Theorem 1.1.Let M∈C1(R2n)be a real-valued function given by

We use the fact that|M(x,y)|≤and

due to(2.1),to conclude,by virtue of(2.3),
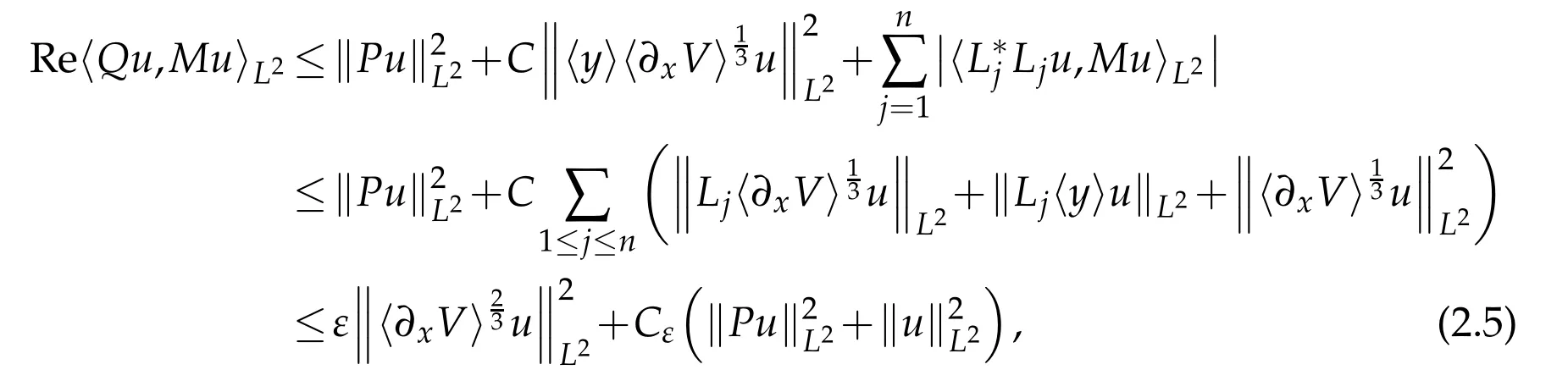
where we use Lemma 2.1 in the last line.As for the term on the left side,we use the fact that Reand
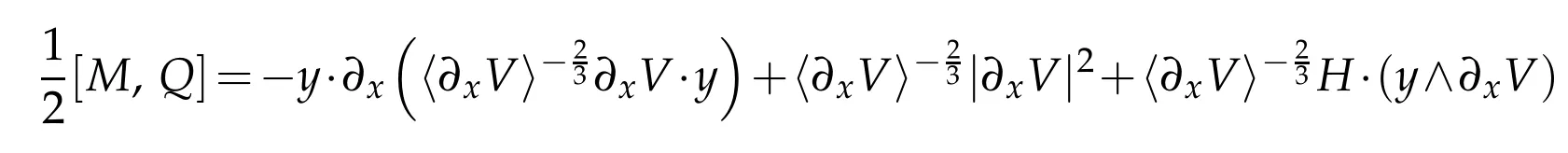
to compute,using(1.3)and(1.4)as well as Lemma 2.1,

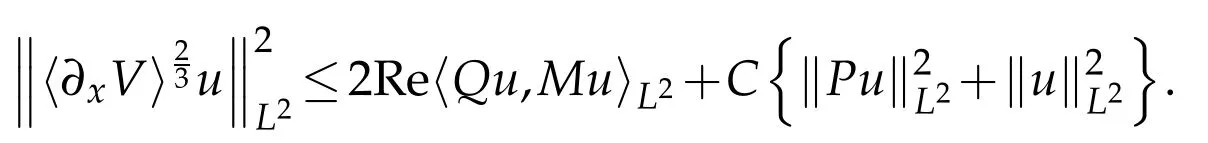
Combining it with(2.5)yields
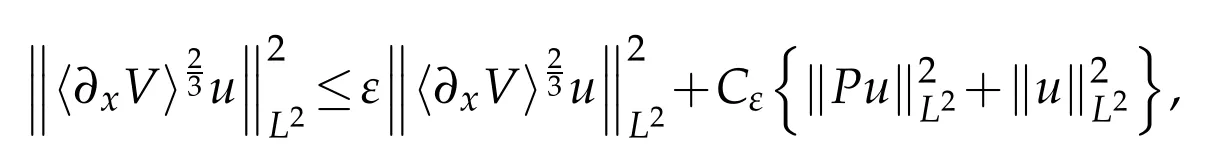
which gives the desired weighted estimate(1.5)if we letεbe small enough.
As an immediate consequence of Lemma 2.1 and the weighted estimate(1.5)we see the estimate
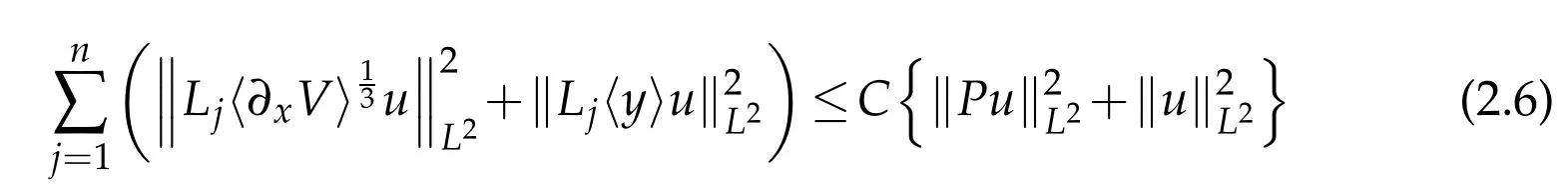
3 Subelliptic estimate
In this section we will prove the subelliptic estimate(1.7)in Theorem 1.1.The proof relies on a localization argument.Firstly we recall some standard results concerning the partition of unity.For more detail we refer to[7,10]for instance.Let g be a metric of the following form
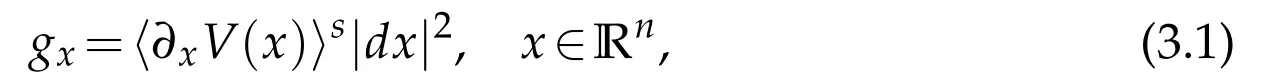
where s is the real number given in(1.4).
Lemma 3.1([11,Lemma 4.2]).Suppose V satisfies the condition(1.4).Then the metric g defined by(3.1)is slowly varying,i.e.,we can find two constants C*,r>0 such that if gx(x-~x)≤r2then
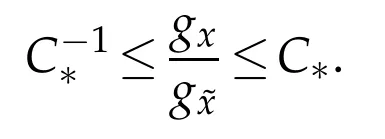
Lemma 3.2([7,Lemma 18.4.4.]).Let g be a slowly varying metric.We can find a constant r0>0 and a sequence xμ∈Rn,μ≥1,such that the union of the balls
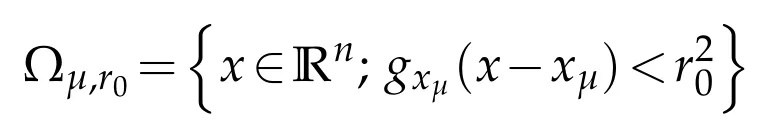
coves the whole space Rn.Moreover there exists a positive integer N,depending only on r0,such that the intersection of more than N balls is always empty.One can choose a family of nonnegative functionssuch that

By Lemmas 3.1 and 3.2 we can find a constant C,such that for anyμ≥1 one has

Lemma 3.3([11,Lemma 4.6]).Letbe the partition given in Lemma 3.2,and let a∈]0,[be a real number.Then there exists a constant C,depending on the integer N given in Lemma 3.2,such that for any u∈(R2n)we have
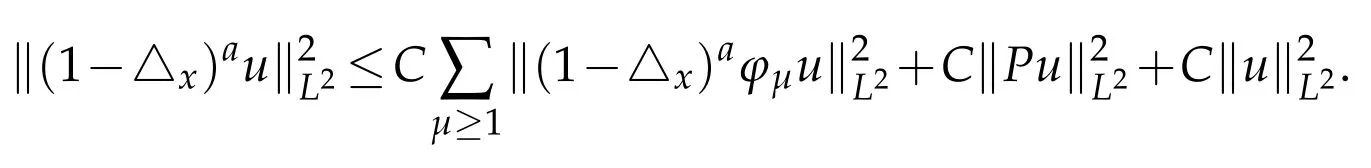
Let{φμ}μ≥1be the partition of unity given in Lemma 3.2.For each xμ∈Rnwe define the operator

Then

with

Lemma 3.4.Suppose H(x)and V(x)satisfy the conditions(1.3)-(1.4)and(1.6).Let Rμbe the operator given in(3.5).Then

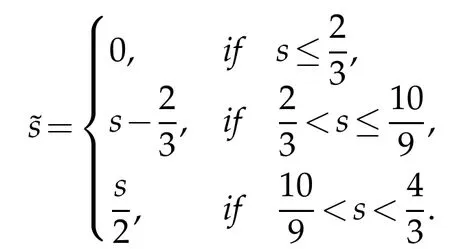
Proof.We write
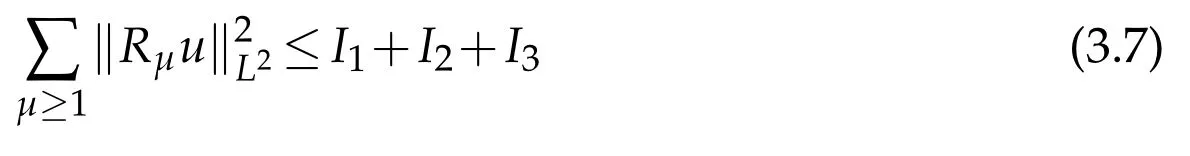
with
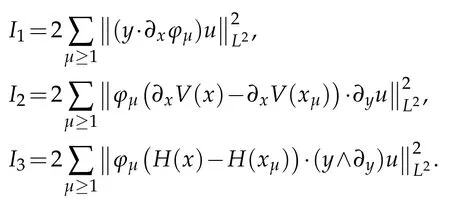
Note it is just finite sum of at most N terms for each Ik,1≤k≤3,recalling N is the integer given in Lemma 3.2.It follows from the last inequality in(3.2)that


the last inequality using(2.6)as well as(2.2)and(2.3).As a result plugging the estimates on Ikinto(3.7)yields

It remains to control the first two terms on the right side,and here we follow the argument in[11]with modification.
(a)The case s≤.In such a case we have
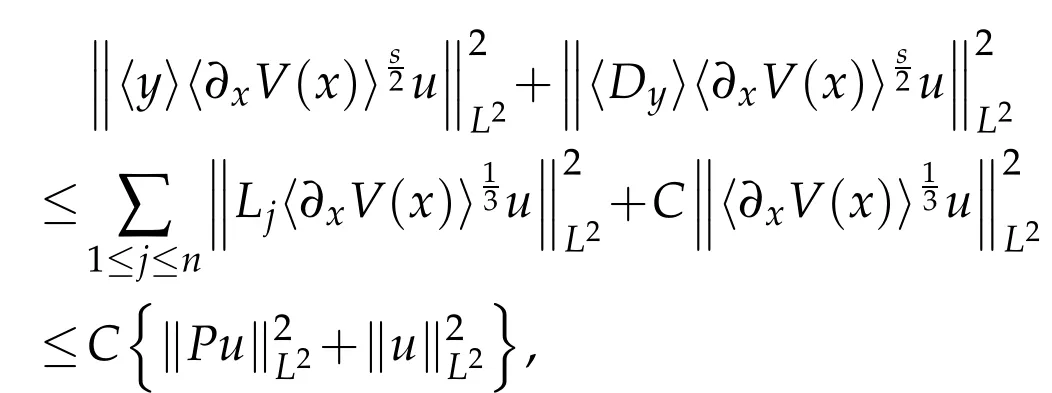
the last inequality using the estimates(1.5)and(2.6)that were established in the previous section.This with(3.8)yields the validity of(3.6)for s.
(b)The caseWe use(2.2)and(2.3)to conclude,for any u∈(R2n),
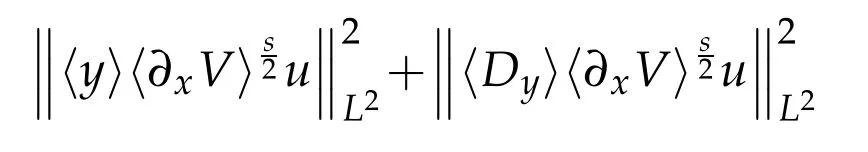

the last inequality using again the weighted estimate(1.5)since s<.This gives the validity of(3.6)for

(c)The case.In this case we use(2.2)and(2.3)to compute
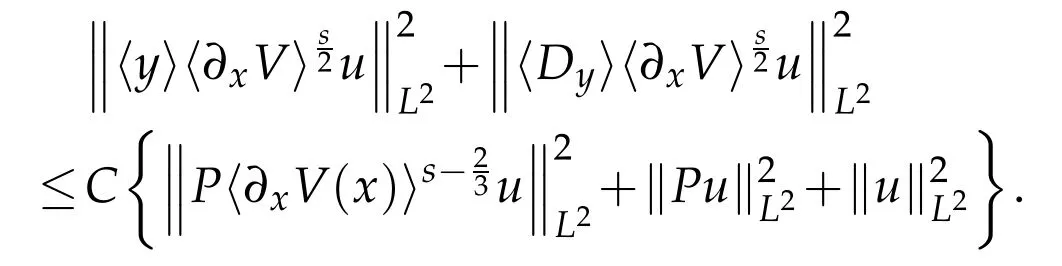
Inserting the above inequality into(3.8)we get the desired estimate(3.6)for<s≤.Thus the proof of Lemma 3.4 is completed.
Lemma 3.5.There is a constant C independent of xμ,such that for any u∈(R2n),one has
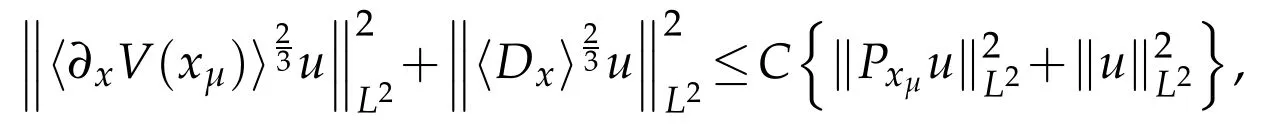
or equivalently,

where the fractional Laplacian is defined by
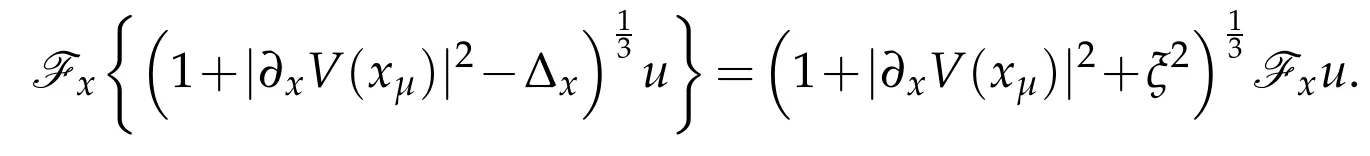
Proof.This follows from classical hypoelliptic technique,seeing for instance[4,Proposition 5.22].We omit it here for brevity.
Completing of the proof of Theorem 1.1:subelliptic estimate.In this part we will prove the subelliptic estimate(1.7).Letφμ,μ≥1,be the partition of unit given in Lemma 3.2 and letτbe given in(1.7).Then we use Lemma 3.3 to compute


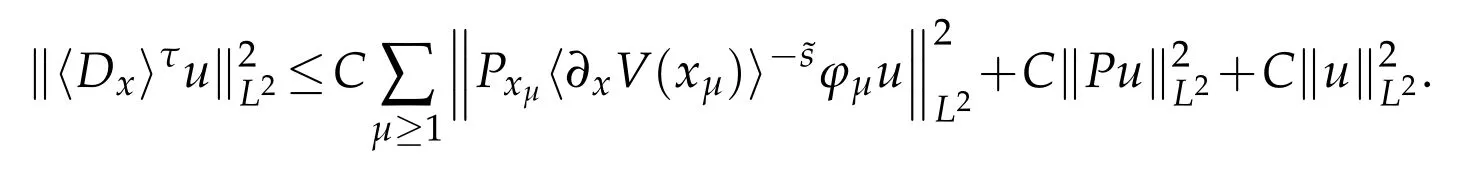
Thus the desired subelliptic estimate(1.7)will follow if the following

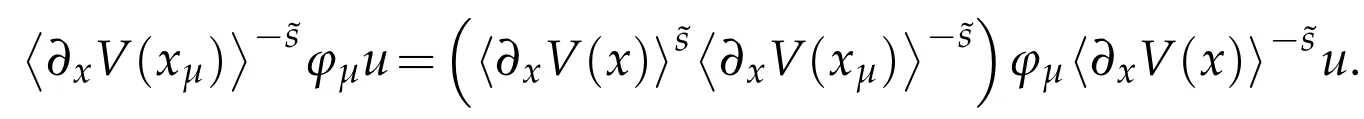
Then

with
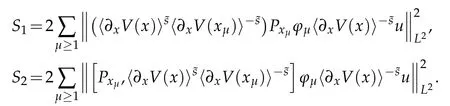
Using(3.3)gives
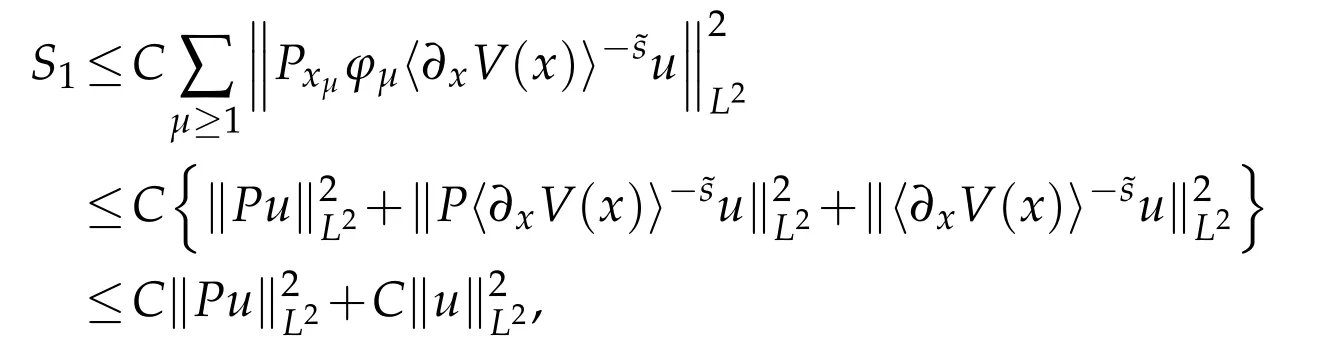
where in the first inequality we use(3.4)and Lemma 3.4,and the last inequality holds because
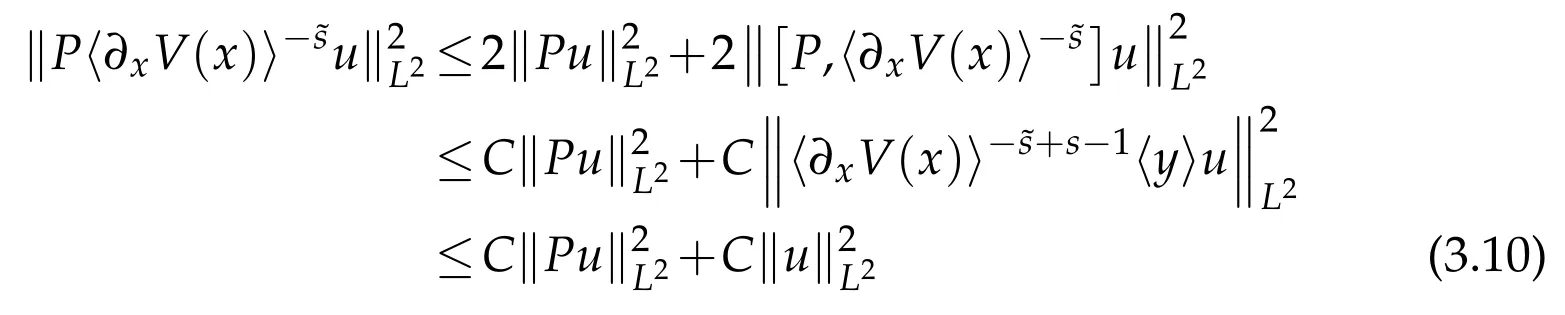
due to(2.2)and(2.3)as well as the fact that-+s-1≤0 and≥0.Similarly,following the argument in(3.10)we have

This with the estimate on S1yields(3.9),and thus the subelliptic estimate(1.7)follows.The proof of Theorem 1.1 is completed.
4 Maximal estimate
In this part we investigate the maximal estimate,i.e.,Corollary 1.1.First we list some commutation relations to be used below.Let Q and Lj,1≤j≤n,be given at the beginning of Section 2.By direct verification we have

and moreover

whereej=(0,···,1,···,0)∈Rnwith only j-th component equal to 1.
Proof of Corollary 1.1.Using(2.2)gives
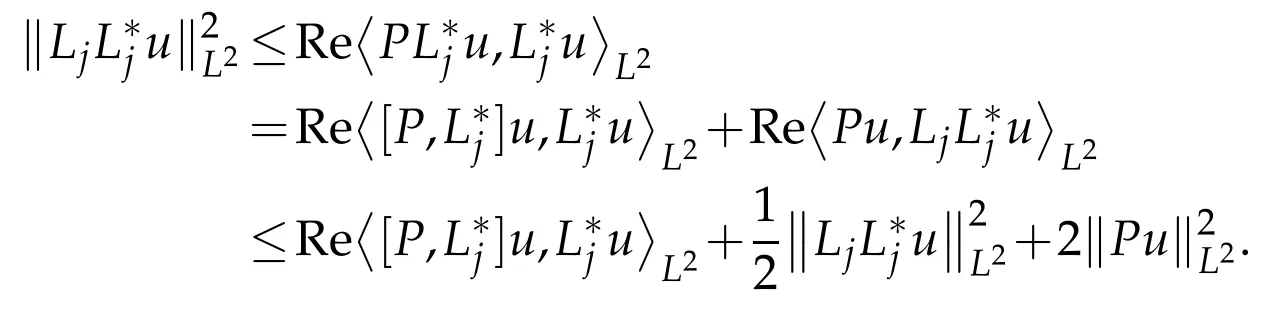
Hence

Moreover it follows from(4.1)-(4.2)that

and thus,by virtue of(1.3),we have
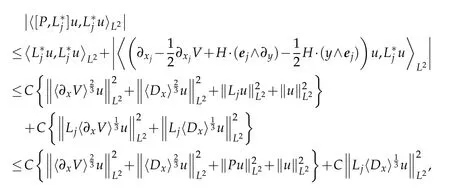
with the last inequality following from Lemmas 2.1 and(2.2).For the last term on the right side we use(4.1)to compute directly,forε>0,

As a result,combining the above estimates we obtain

which,together with(4.3)and the estimates(1.5)and(1.7)withτ=23therein,yields

The gives the assertion in Corollary 1.1,completing the proof.
Acknowledgments
This work was supported by NSFC(Grant Nos.11961160716,11871054,11771342)and Fundamental Research Funds for the Central Universities(Grant No.2042020kf0210).
