空心光束在非Kolmogorov湍流传输路径上的区域分割
2021-05-13陈晓文魏小琴汤明玥邓涵凌
陈晓文,魏小琴,汤明玥,邓涵凌
(1.川北医学院 医学影像学院,南充 637000;2.川北医学院 基础医学院,南充 637000)
引 言
激光束在大气中的传输研究对光通讯、卫星遥感等实际应用有一定指导意义[1],值得科研工作者对其展开相关研究。然而,复杂的大气环境需要找到一个合适的湍流模型来进行描述,前期科研工作者们均采用常规的Kolmogorov功率谱来研究湍流[2-5],但实际湍流中含有各向异性统计特征的区域,由湍流广义指数和广义幅度因子描述的非Kolmogorov湍流功率谱[6]所得结果与试验数据更相符,具有一定的普适性。因此,国内外同行们对激光束在非Kolmogorov湍流模型中的传输特性研究产生了浓厚的兴趣,并于近期展开了一些相关研究[7-12]。研究发现,光束在湍流中传输的光强分布、相干度、扩展等均对湍流广义指数表现出非单调的变化。光束扩展是激光束传输特性中值得重点关注的一个方面,目前已有大量的文献[13-18]中对激光束在湍流中的扩展展开了相关研究,并得到了一些有意义的结论。空间衍射及湍流介质是造成光束扩展的两个主要因素,那么值得进一步讨论的是,可以考虑把光束的传输路径分割为3个区域:主要因空间衍射导致光束扩展的区域、空间衍射和湍流共同影响光束扩展的区域及主要由湍流导致光束扩展的区域。因此,本研究中利用湍流距离将光束的传输路径分割为3个区域,并对3个区域的范围及不同区域内光束的扩展进行详尽的讨论。
另一方面,空心光束的中心光强分布为零,具有特殊的性质和实际应用[19-20]。空心光束在生物医学、激光加工及微观粒子的冷却与囚禁等方面应用广泛,关于空心光束的产生、特性仍是目前研究的热点。为此,科研工作者们就湍流对空心光束传输特性的影响开展了大量研究[21-22]。然而,迄今为止,关于空心光束在湍流中的区域分割研究尚未涉及。
综上所述,本文中依据湍流距离,将空心光束在湍流中的传输路径分割为3个区域,详尽讨论了3个区域的范围与光束参量和湍流参量之间的关系,同时直观地展示了光束在3个区域内的扩展情况。此外,详细讨论了光束参量的选取与湍流是否在瑞利区间内就对光束扩展构成影响之间的关系。
1 光束理论模型
空心光束的理论模型可由两束不同束宽(w0和w0η分别为两束光束的束宽,且0<η<1)的平顶光束之差构成。那么,空心光束的复振幅可写为:

(1)
式中,η为光束遮拦比;M,N为光束阶数;αm,αn,pm和pn的表达式详见参考文献[3]。
则空心光束在z=0处的光强表达式为[3]:
I0(r1′,r2,0)=U0*(r1′,0)U0(r2′,0)=
I01(r1′,r2′,0)+I02(r1′,r2′,0)-
I03(r1′,r2′,0)-I04(r1′,r2′,0)
(2)
式中,U0是环状光束的复振幅,U0*是U0的共轭;r1′和r2′分别是U0函数、U0*函数中z=0处垂直于传输方向平面上的空间位置。其中,
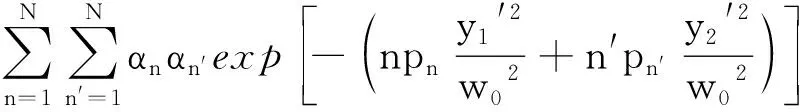
(3)
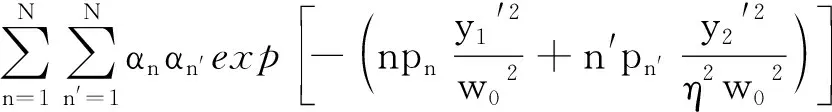
(4)
式中,x1′和y1′是r1′中的直角坐标;x2′和y2′是r2′中的直角坐标;m′,n′是分别对应x2′和y2′的取值阶数。将(3)式中的w0换为ηw0,得到I02(r1′,r2′,0);将(4)式中的w0与ηw0互换,得到I04(r1′,r2′,0)。
为展示空心光束在z=0处光强分布等高线图,可令(3)式中r1′=r2′,并选取光束参量w0=0.02m,η=0.6,M=N=4,见图1。
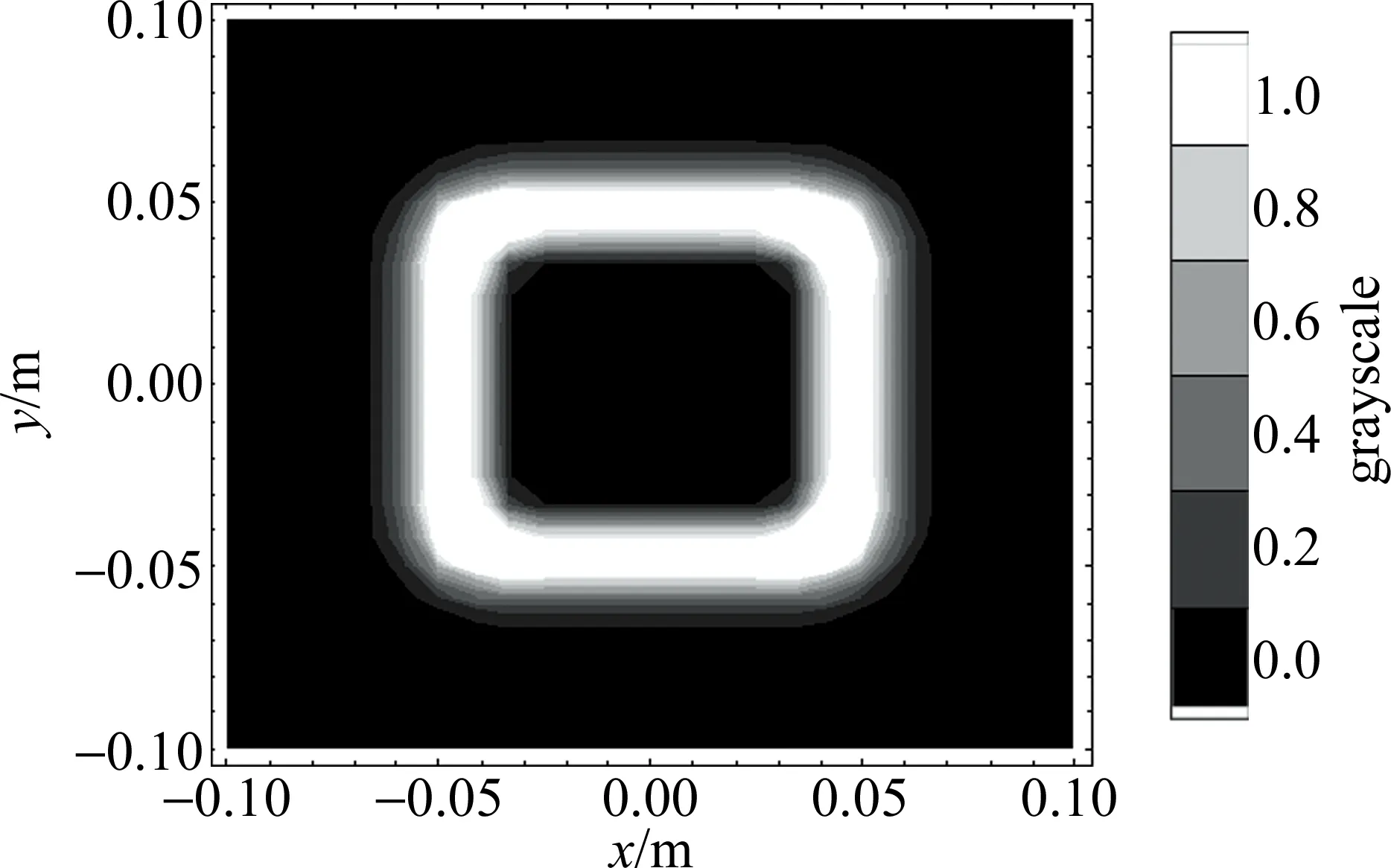
Fig.1 Contour of intensity distribution of hollow beams
2 解析式推导
在光束的传输路径上,光束的二阶矩宽度定义为[3]:
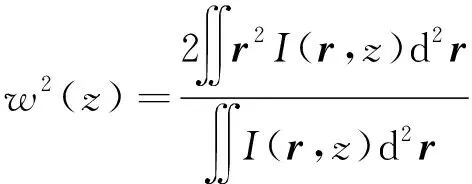
(5)
式中,I(r,z)为空心光束传输路径上z处的光强分布,r为传输路径上的空间位置。利用广义惠更斯-菲涅耳公式,I(r,z)可表示为:
〈 exp[ψ*(r,r1′,z) +ψ(r,r2′,z)]〉m
(6)
式中,波数k=2π/λ;ψ(r,r2′,z)是湍流介质的复相位结构函数,ψ*(r,r1′,z)是其共轭函数。湍流系综平均〈〉m表示为[4-5]:
〈exp[ψ*(r,r1′,z)+ψ(r,r2′,z)]〉m=
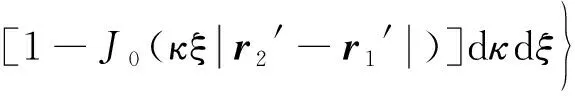
(7)
式中,J0()为零阶贝塞尔函数,κ表示空间频率,ξ为传输路径参量,κm为低空间截止频率,κ0为高空间截止频率。
综合(2)式、(6)式及(7)式,并代入(5)式,采用积分变换法,并经繁琐的积分运算,可求得空心光束传输于非Kolmogorov湍流中的二阶矩宽度解析式:
w2(z)=w12+w22z2+Tz3
(8)
其中,
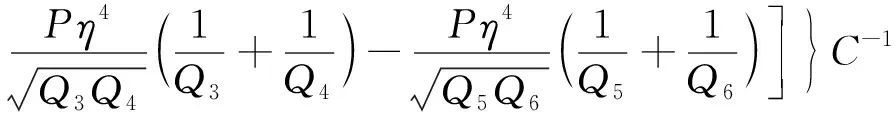
(9)
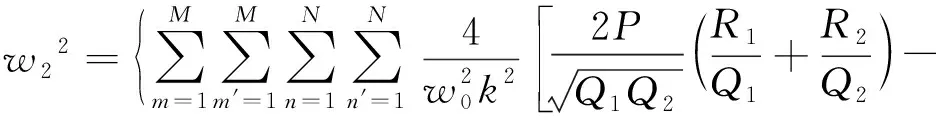
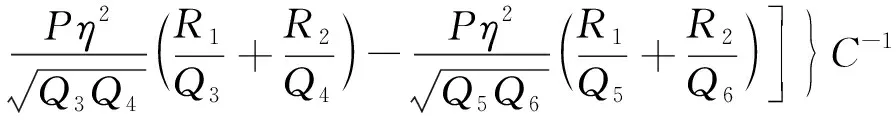
(10)
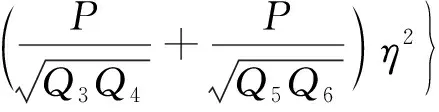
(11)
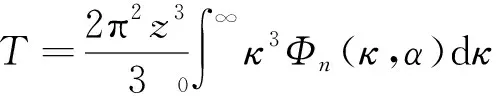
(12)
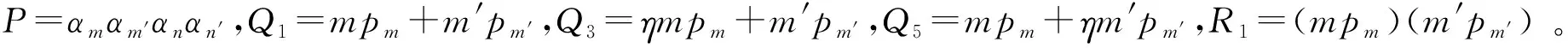
瑞利区间的定义:光束的横截面积扩展达z=0处两倍时的传输距离[17],即:
w2(zR)=w12+w22z2+Tz3=2w12
(13)
求解可得:
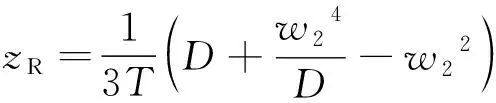
(14)
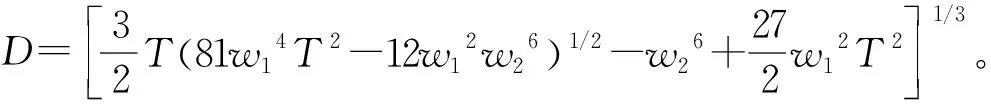
另一方面,湍流距离表示为光束的横截面积因受湍流影响而扩展10%及90%的传输距离[18],分别用zt,1和zt,2表示:
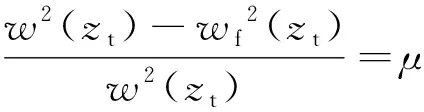
(15)
式中,wf为自由空间中的束宽,wf2=w12+w22z2。求解三次方程,可得到空心光束传输于非Kolmogorov湍流中的湍流距离zt解析表达式:
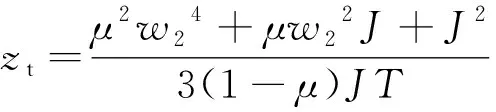
(16)
式中,
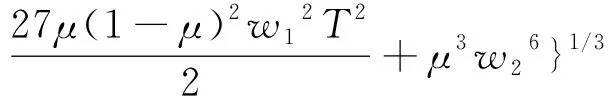
(17)
显然,当μ=10%时,(16)式表示zt,1;当μ=90%时,(16)式表示zt,2。
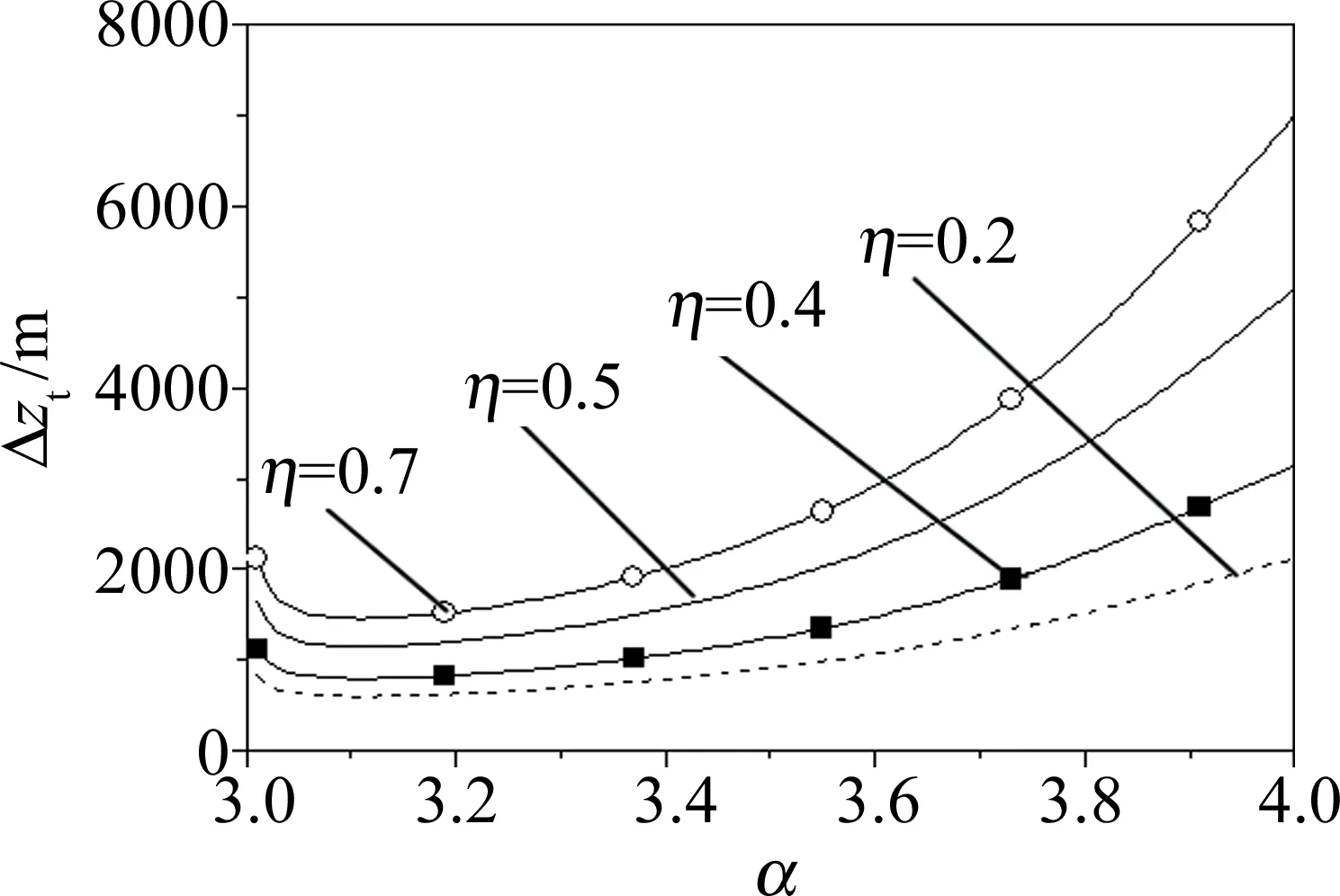
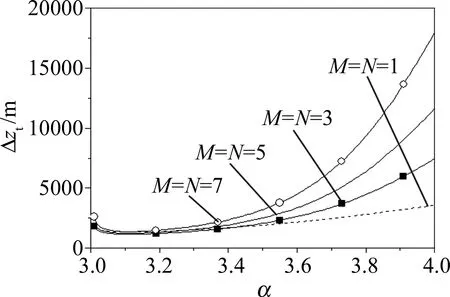
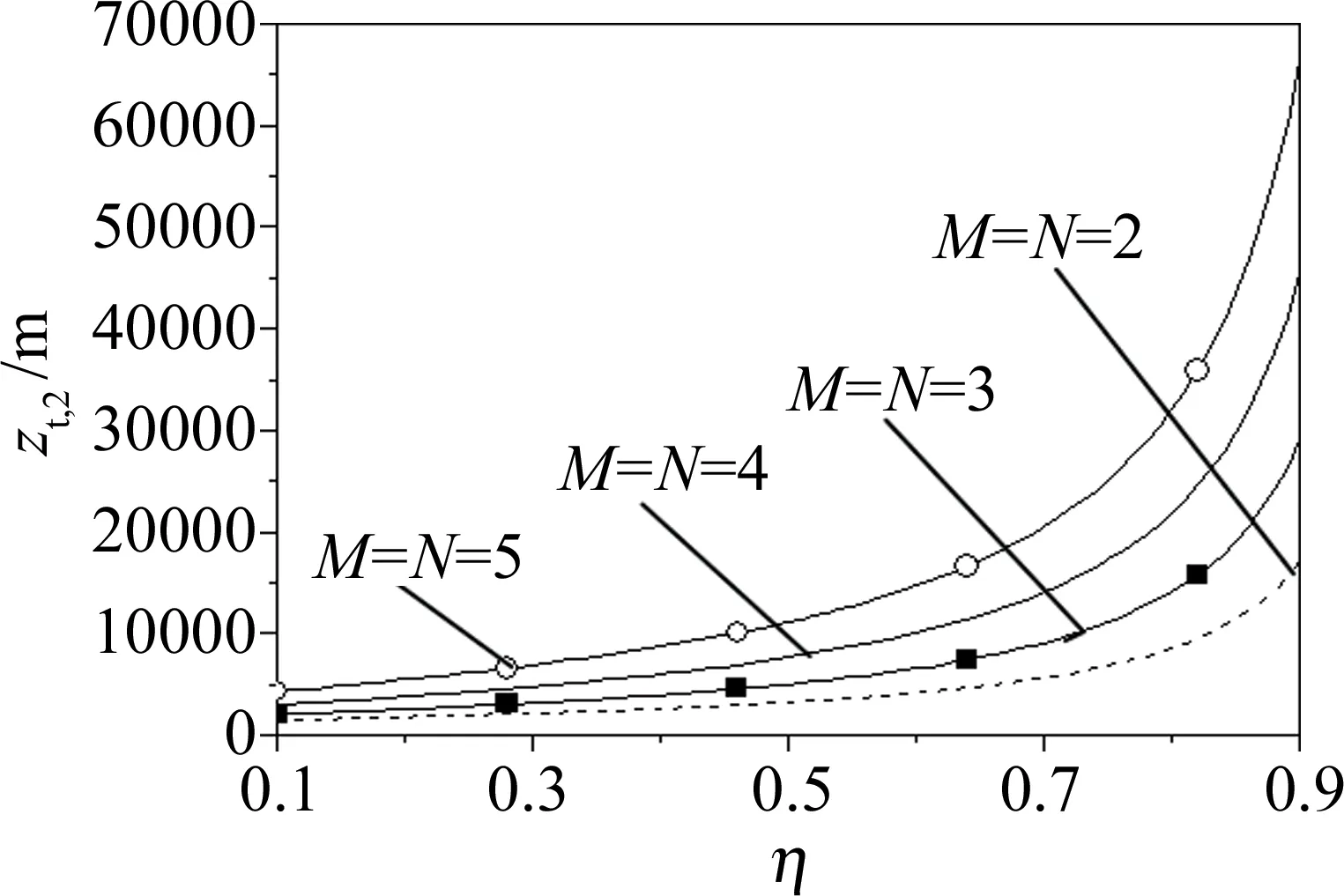
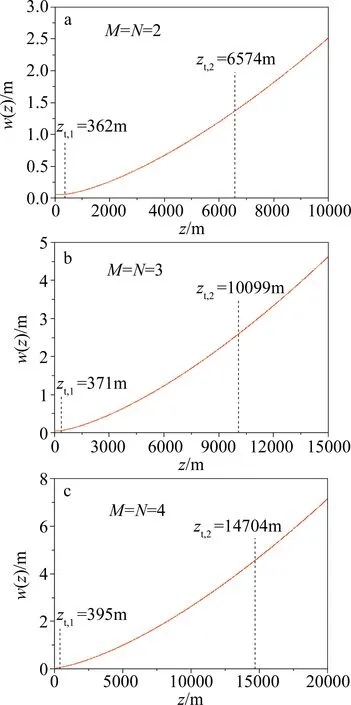
应当指出的是,光束的传输路径可被zt,1和zt,2划分为3个区域:(1)区域Ⅰ:0 Fig.2 zt,1,zR versus α Fig.3 zt,1/zR versus η with different value of versus M(and N) 图4为区域 Ⅰ 长度zt,1在不同M(及N)下随η的变化情况。可以发现,zt,1随M(及N)和η的增大而增大,其物理解释为:M(及N)和η越大,光束的原有扩展越大,湍流对其扩展的影响越小,则区域 Ⅰ 的长度越大。 Fig.4 zt,1 versus η with different value of M(and N) 区域 Ⅱ 的长度Δzt=zt,2-zt,1在不同η和M(及N)下随α的变化见图5和图6。同样,Δzt也随α的增大而先减小再增大(当α=3.11时出现一个极小值),且Δzt随η和M(及N)的增大而增大。此外,α取较小值时,各条曲线差异较小,随α的增大,Δzt差异更为明显。 Fig.5 Δzt versus α with different value of η Fig.6 Δzt versus α with different value of M(and N) 图7和图8中分别为区域Ⅲ的起点zt,2随α和η的变化情况。由图可看出,zt,2同样随α的增大而先减小再增大(当α=3.11时出现一个极小值),且随M(及N)和η的增大而增大。为了更加直观展示空心光束在湍流中的扩展,图9和图10中给出了光束二阶矩宽度w(z)在不同M(及N)和η下随传输路径z的变化情况,同时给出了相应的zt,1和zt,2的具体数值。由图可知,光束在传输路径上依次进入区域Ⅰ、区域Ⅱ及区域Ⅲ,其二阶矩宽度w(z)的增大变得更加剧烈,且zt,1和zt,2随M(及N)和η的增大而增大,这与上述研究结果一致;同时,发现随着参量M(及N)和η的增加,zt,1缓慢增加,而zt,2的增大却十分显著。这说明光束参量M(及N)和η对区域Ⅱ长度和区域Ⅲ的起始点影响更大。 Fig.7 zt,2 versus α Fig.8 zt,2 versus η with different value Fig.9 w(z) versus z with different value of M(and N) Fig.10 w(z) versus z with different value of η 建立空心光束理论模型,并推导其传输于湍流中的二阶矩宽度、瑞利区间及湍流距离解析式。同时,利用湍流距离把传输路径分割为3个区域,并对扩展区域的分割范围及不同区域内光束的扩展进行了数值理论分析。 (1)区域Ⅰ、区域Ⅱ的长度及区域Ⅲ的起始点都随α的增大而先减小再增大(当α=3.11时出现一个极小值),且随M(及N)和η的增大而增大。 (2)M(及N)取值较小时(M(及N)<3),不论η取何值,湍流在瑞利区间内对光束扩展的影响都不能忽略;M(及N)和η越大,越容易忽略湍流在瑞利区间内对光束扩展造成的影响。 (3)α取较大值时,不同M(及N)和η下区域Ⅱ长度的差异更为显著。 (4)传输路径上,光束依次进入区域Ⅰ、区域Ⅱ及区域Ⅲ,其光束扩展依次变得更加剧烈;随着参量M(及N)和η的增加,区域Ⅰ的长度缓慢增加,而区域Ⅱ长度和区域Ⅲ的起始点增加更为显著。应当特别指出:各类激光束在湍流中传输,都可以采用湍流距离将光束传输路径分割为3个区域,3个扩展区域的范围均与光束参量和湍流参量相关。本研究中所指出的区域Ⅰ、区域Ⅱ的长度及区域Ⅲ的起始点都随α的增大而先减小再增大,这一结论也能适用于其它各类光束。究其原因:本研究小组[4]曾在讨论相干光束在湍流中的扩展及方向性时指出,任意相干光束在湍流中二阶矩宽度的解析式均可表达为本文中的(8)式,即二阶矩宽度均由3项组成,前两项与光束参量相关,第3项湍流项是独立存在,因而各类光束的扩展受湍流影响的变化趋势是一致的,结合(7)式和(16)式可知,湍流广义指数对空心光束湍流距离(区域Ⅰ、区域Ⅱ的长度及区域Ⅲ的起始点)的影响也能适用于其它光束。本研究结果对于空心光束传输于湍流中的相关应用有指导意义。3 数值计算结果与分析
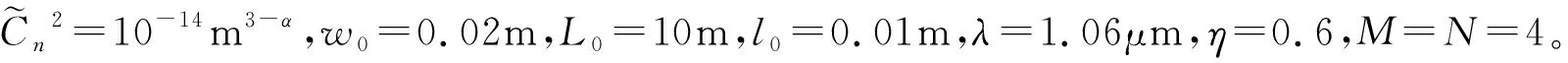
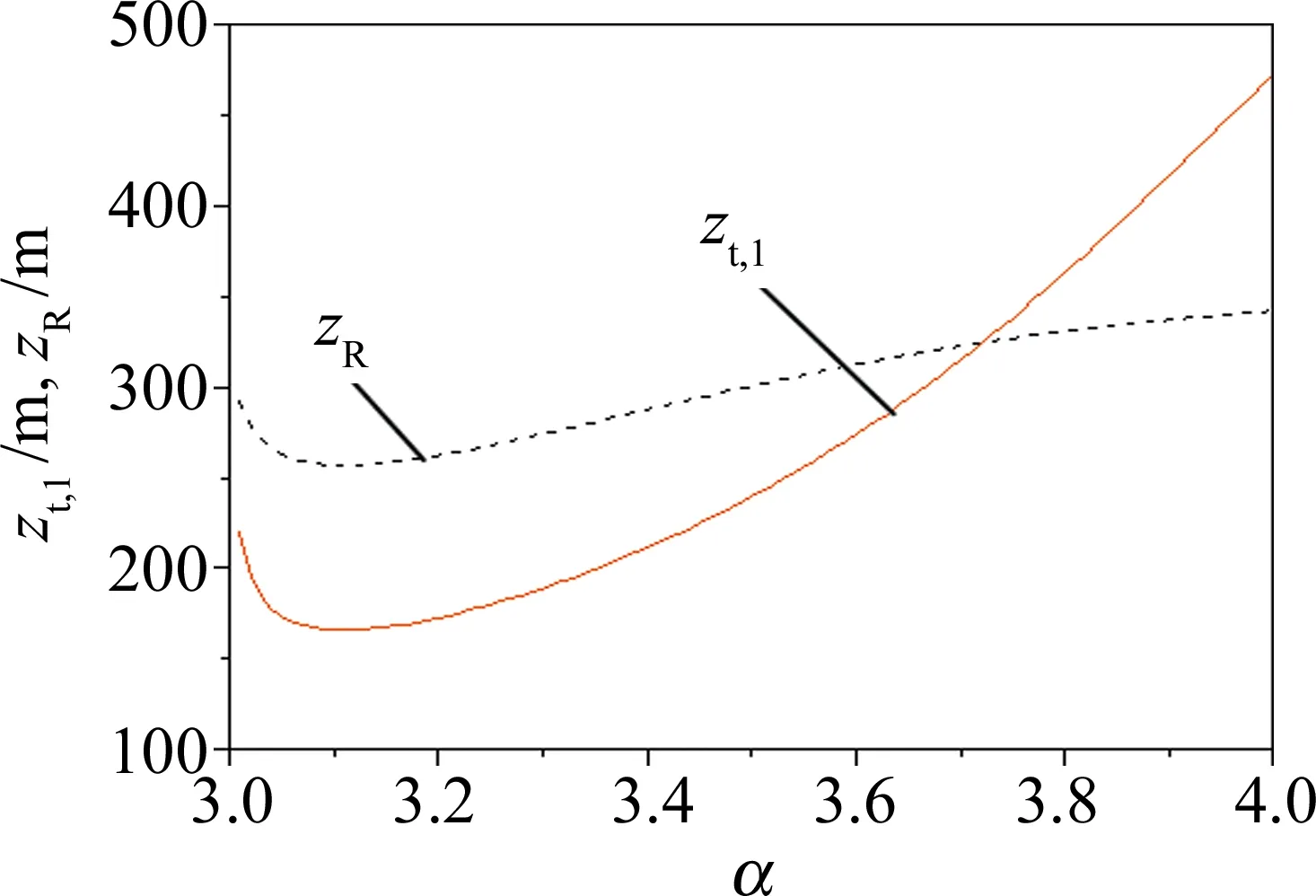
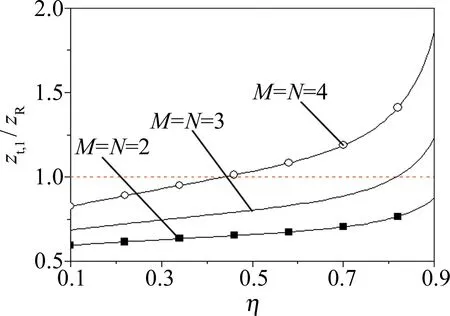
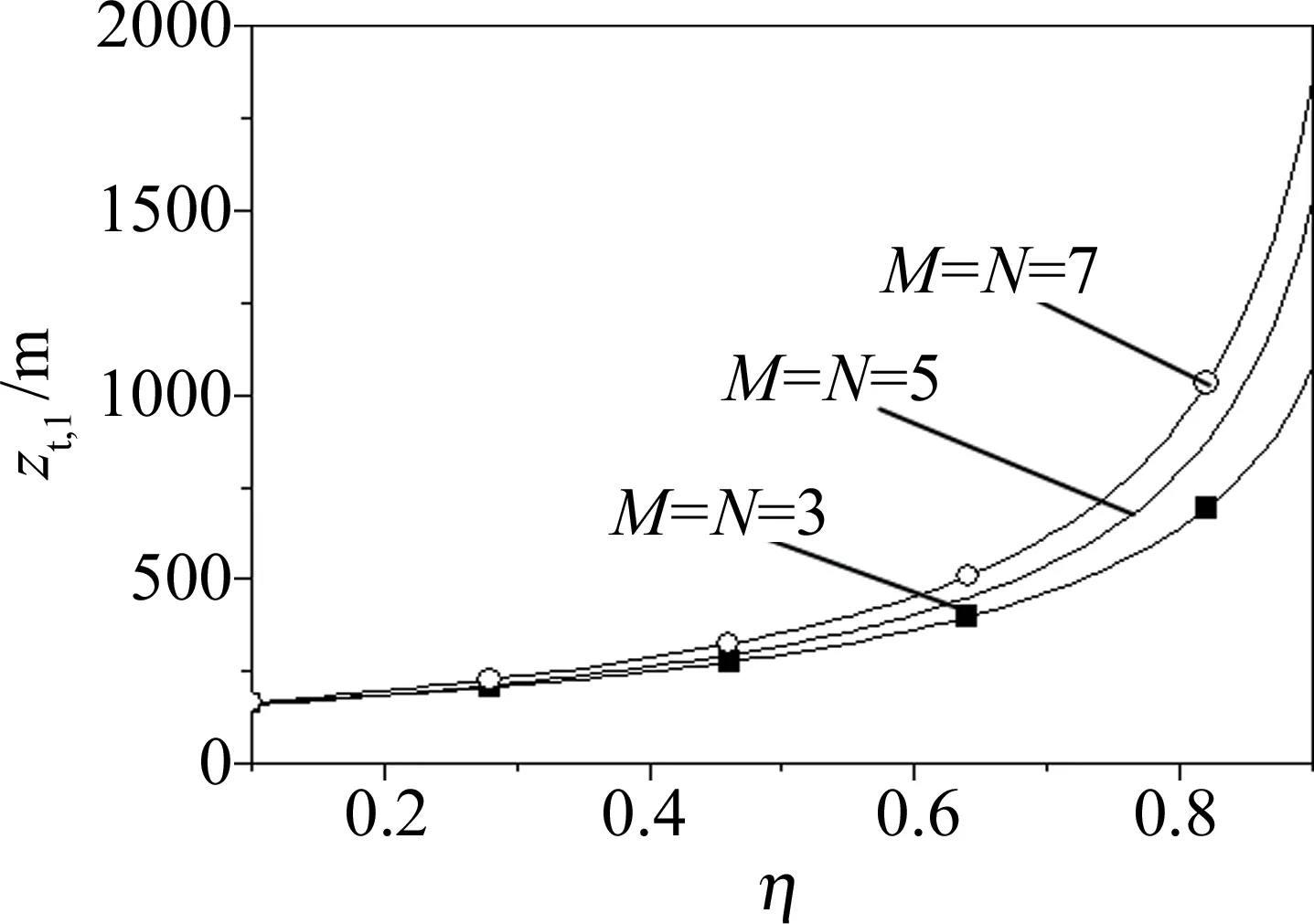


4 结 论
