基于双芯光子晶体光纤耦合微扰传感器
2021-05-13陈奂文王语章
蔡 俊,陈奂文,董 超,高 翔,王语章
(西南科技大学 理学院,绵阳 621010)
引 言
光子晶体光纤(photonic crystal fiber,PCF)作为一种新型光纤,具有独特的结构和传输特性,近年来一直成为人们关注的焦点。PCF具有大模场面积、单模传输、高非线性、高双折射和超低损耗等特性[1-3],可广泛应用于多种设计和各个领域,实现高效传输和高精度测量等目的。随着PCF研究的不断深入,逐渐出现各类PCF结构,而双芯光子晶体光纤(dual-core photonic crystal fiber,DCPCF)作为一重要分支[4],被重点关注。对于DCPCF的传感研究,可根据PCF结构设计的多变性,以及双芯结构的耦合特性[5],实现高精度传感器件的设计。光纤传感器件出现的种类多样,如光纤光栅传感器[6]、光子晶体光纤传感器[7]、光子晶体填充式传感器[8]、定向耦合型传感器[9]以及光纤表面等离子体传感[10-11]等等,但大多传感器件都存在着传感精度不高、监测范围小或者制作工艺艰难和昂贵等问题,难以达到实际需求。
对于DCPCF,根据其光场在波导中的耦合传输特性,可以应用于不同环境的检测,实现高精度和宽范围测量的目的。目前对于双芯耦合传感技术的研究主要局限于一般的纤芯耦合和孔隙填充,并没有较为全面的利用PCF的结构优势和填充材料的物理特性。
作者则提出一种基于结构上的新型DCPCF耦合微扰传感器,主要通过RSOFT中Beampronp模块的有限差分光束传播法(finite-difference beam propagation method,FD-BPM)对该结构的波导传输进行检测分析。该设计根据PCF的结构特点——孔隙多样性,引入耦合微扰填充缺陷并结合填充技术,利用结构优势和填充材料的物理特性,进一步提升光子晶体光纤传感性能。根据PCF的耦合传输特性,所提出的一种DCPCF高灵敏温度传感器,其结构小巧、轻便,在传感精度上有很大提升,同时具有加工工艺简单、成本较低等优势,可广泛应用于各大领域,具有一定的实用和参考价值。
1 理论模型
基于DCPCF耦合微扰传感器的结构如图1所示。其包层为均匀六边形空气孔结构,空气孔直径d=1.6125μm,空气孔间距Λ=4.3μm,空气孔直径与空气孔间距之比d/Λ=0.375,根据PCF的等效归一化频率表达式[12]:
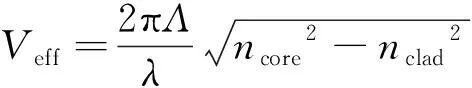
(1)
式中,Λ为空气孔间距,λ为波长,ncore和nclad分别为纤芯折射率和包层折射率。当Veff<0.45时,满足无截至单模传输条件。PCF中心两侧引入双纤芯波导结构,双纤芯呈水平轴对称,为光波耦合传输路径;周围引入两个填充大孔缺陷,直径D=12.9μm,距离中心点距离l=10μm;填充大孔缺陷通过竖直双曲线型缺陷层连通,曲率半径Rq=7.5μm,其腰间距离Lw=1.6025μm,形成耦合微扰层。大孔缺陷及耦合微扰层构成“哑铃”型折射率液体填充区域。其中填充区域两大孔有利于快速受热,耦合微扰层与双纤芯结构能对折射率和耦合间距的变化做出敏感反映。对折射率液体填充区域,本研究中选择乙醇为填充材料,实现高精度温度传感。
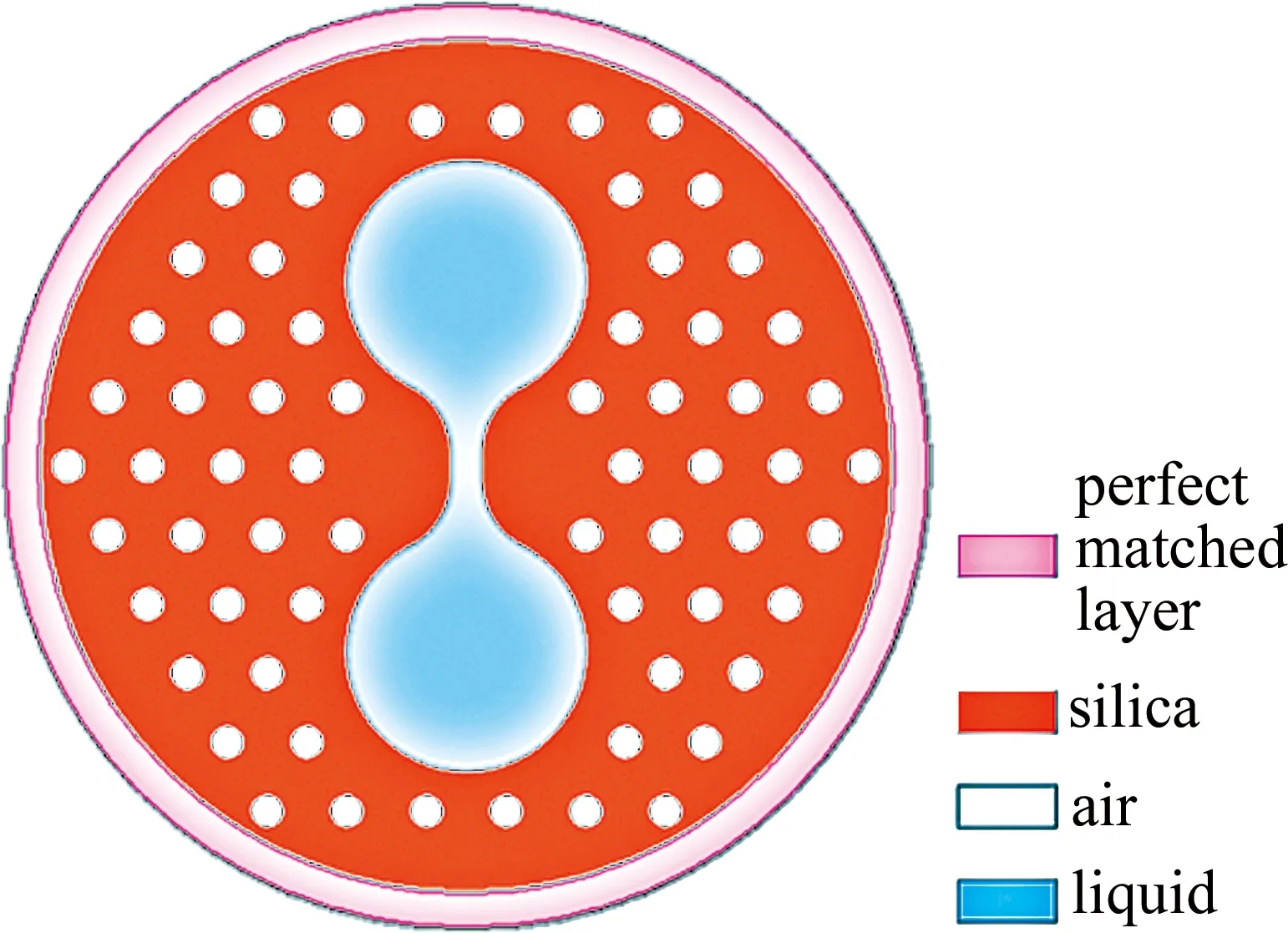
Fig.1 Cross section of photonic crystal fiber with dual-core coupling perturbation structure
结构中,光纤基底材料采用石英玻璃,其折射率可根据Sellmeier方程算出[13]:
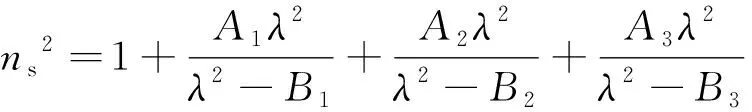
(2)
式中,ns为石英玻璃折射率;B与C为Sellmeier方程系数,不同材料各系数不同,可在光学手册中查询相关系数。此处依次为A1=0.6961663,A2=0.4079426,A3=0.8974794;B1=4.67914826×10-3μm2,B2=1.35120631×10-2μm2,B3=97.9340025μm2,代入各系数即可确定光纤基底材料随波长变化的折射率关系。
该设计对温度的高精度检测,主要根据外界环境温度的改变,影响耦合微扰层中填充液体的折射率和体积,使纤芯有效折射率和耦合间距发生变化,让光场在双芯耦合波导中传输时,输出不同透射谱,实现温度的高精度检测。根据耦合理论,在双芯耦合分析时,由温度造成的液体折射率变化和体积膨胀,可进行单独分析,不仅能实现两变量的单独检测,还能结合两变量对温度的高精度传感进行全面分析。
液体填充区可根据使用条件,选择性填充不同物理性质的检测液体。乙醇具有较好的热光效应,其折射率和温度在一定温度范围具有较好的线性变化关系,且成本低廉、易填充。乙醇的热光系数α=3.94×10-4/K,热膨胀系数β=1.09×10-3/K,随着温度T的变化,其折射率变化关系为[14]:
n=n0-α(T-T0)
(3)
式中,n为不同温度T下的乙醇折射率;n0为温度T0=293.15K时的乙醇折射率,n0=1.36048;T0为初始温度。
在环境温度变化过程中,除造成填充液体折射率变化外,还会导致乙醇受热膨胀,增大双芯耦合间距,乙醇受热膨胀与耦合距离的变化关系可以表示为[15]:
L=L0+L0β(T-T0)
(4)
式中,L为不同温度T下的耦合间距,L0为初始间距,L0=1.6025μm。由于石英玻璃的热光系数α=8.60×10-6/K,热膨胀系数β=5.5×10-7/K,与填充材料相差两个量级以上,因此忽略温度对石英折射率和热膨胀的影响,而只考虑温度对填充材料折射率变化及液体热膨胀对耦合间距的影响。
2 特性分析
2.1 DCPCF的耦合传输特性
根据耦合理论,在DCPCF耦合传输时,仅在耦合介质和耦合间距达到一定条件时,光场才能在两纤芯发生稳定耦合。该结构在入射波长为1.550μm时,分别选择折射率区间为1.30~1.40,耦合间距区间为1.4μm~2.0μm进行分析。对于该折射率区间,两纤芯功率稳定耦合,端口透射率与折射率之间的关系如图2a所示,该波长下的端口透射率随折射率的增加逐渐变得敏感。端口透射率与耦合间距之间的关系如图2b所示,在该波长下耦合间距在1.48μm~1.76μm左右时,两纤芯功率才能稳定耦合。
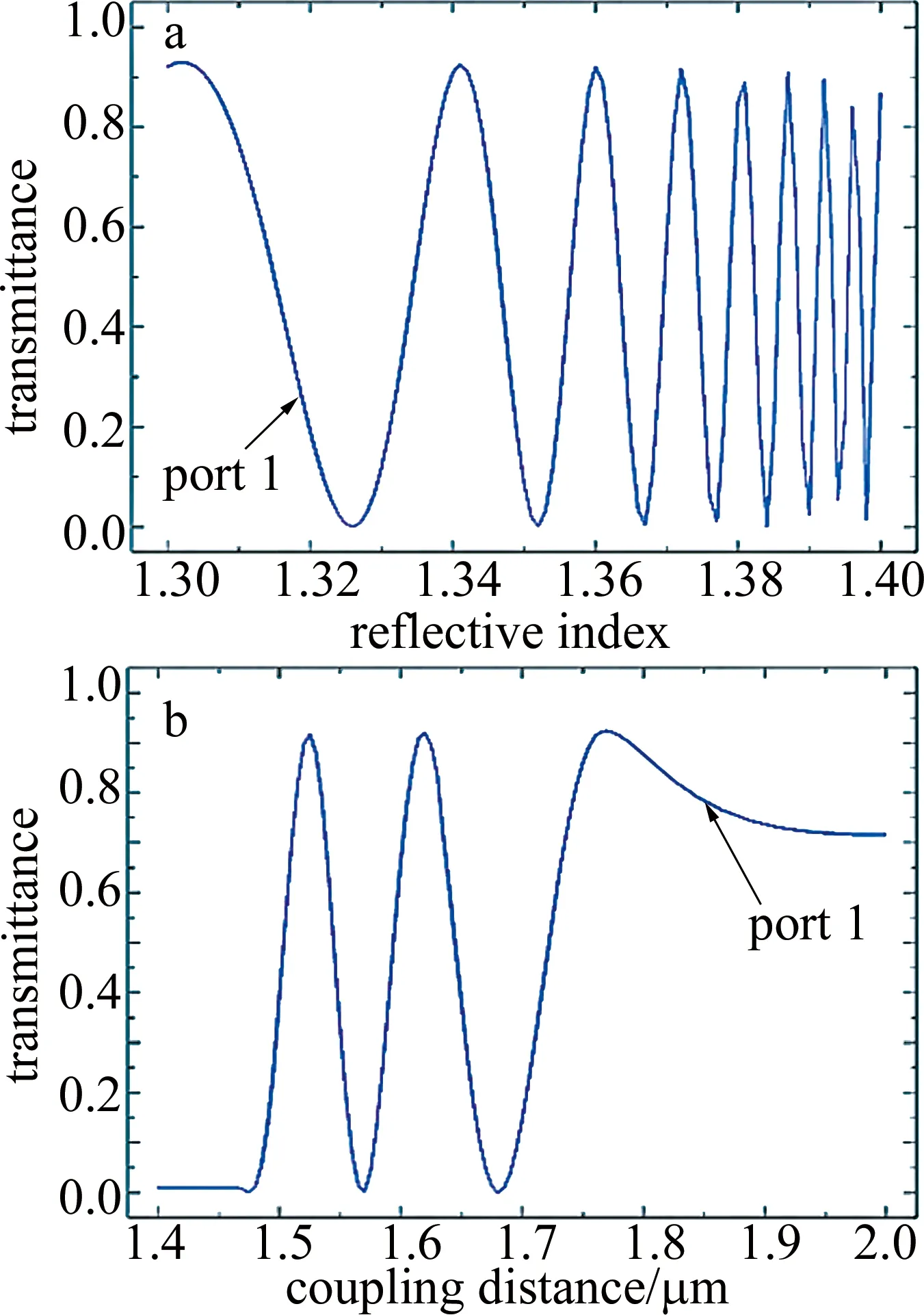
Fig.2 a—relationship between the refractive index of the filled area and port transmittance when wavelength is 1.550μm b—relationship between the coupling distance and port transmittance when wavelength is 1.550μm
根据微扰层填充材料折射率、耦合间距与功率耦合的关系,在以下研究中,将选择合适的折射率和耦合间距,分析光子晶体光纤双芯耦合的传输特性和传感性能。在波长为1.550μm、折射率为1.361时,满足双芯耦合微扰结构实现光功率的稳定耦合传输条件。仿真分析得到双芯耦合传输过程如图3所示。
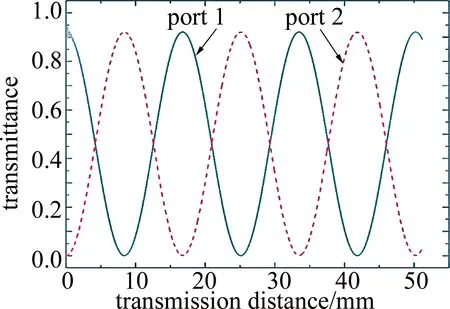
Fig.3 When the wavelength is 1.550μm,the optical power periodically couples with increasing transmission distance
功率在两纤芯波导中耦合传输时,完全符合耦合理论公式所推导的结论。在入射波长为1.550μm时,随着传输距离的增加,双芯波导中的功率发生周期性耦合,耦合长度Lc=8367μm,具有很好的稳定性和周期性。在改变波长时,根据双芯耦合理论,耦合长度将发生变化,结果如图4所示。
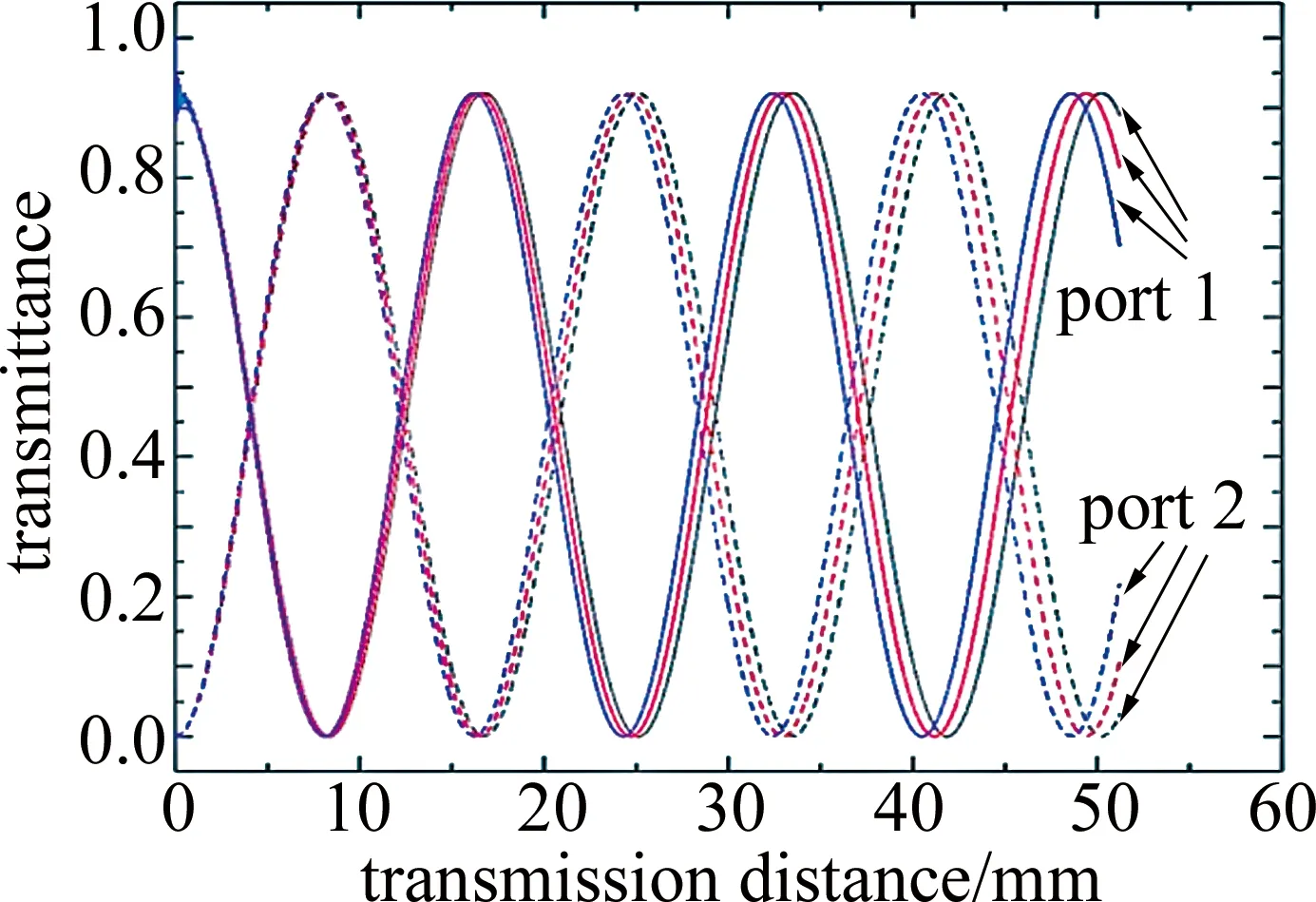
Fig.4 When the wavelengths are 1.550μm,1.555μm and 1.560μm,the power in the two waveguides periodically couples with the transmission distance
在入射波长依次为1.550μm,1.555μm,1.560μm时,对应耦合长度分别为8367μm,8234μm,8099μm,耦合长度随波长增加逐渐变短。由于DCPCF长度确定,对不同的入射波长将在端口对应不同透射率。因此可通过在端口输入一段波长的光源,就能够得到不同波长下的透射率,最终形成端口输出谱线。为得到波段在1.3μm~1.6μm左右的透射峰,在相关参量不变的情况下,通过仿真分析,发现在波段为1.47μm~1.57μm,填充区折射率n为1.364时,该波段下能够输出完整的透射峰,如图5所示。
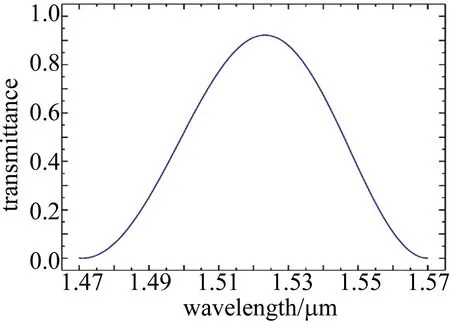
Fig.5 The incident waveband is 1.47μm~1.57μm,when the filled area is refracted n=1.364,the transmission spectrum of the output port
该条件下的透射峰值在1.523μm,半峰全宽(full width at half maxium,FWHM)为51nm。根据各参量对双芯耦合传输的影响,通过改变微扰层填充区的折射率,得到不同的透射谱线,最终根据透射谱的峰值移动来反映折射率的变化。
2.2 DCPCF的折射率检测特性
在相关参量不变的情况下,微扰层填充区折射率n依次为1.361,1.362,1.363,1.364,1.365时,仿真得到的透射谱如图6所示。

Fig.6 The filled area of the perturbation layer is the transmission spectrum at different refractive indices
在折射率发生变化时,透射谱峰值发生了明显的移动,随着折射率的增加,透射峰发生蓝移。根据不同折射率液体的透射谱线,以1.361为基础,其峰值在1.544μm,半峰全宽为51nm,随折射率的增加,对应透射峰的峰值依次为1.537μm,1.530μm,1.523μm,1.516μm,半峰全宽恒定为51nm。透射峰值和折射率的变化灵敏度可用以下表达式确定[16]:
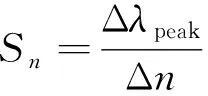
(5)
式中,Δλpeak表示两个透射峰值的移动量,Δn表示折射率差。计算可得折射率检测灵敏度Sn=7000nm/RUI,可用于实现对折射率变化相关的高精度检测技术。
2.3 DCPCF耦合间距检测特性
同理,根据耦合间距与双芯功率耦合的关系,耦合间距发生变化时,也会影响光传输时的耦合长度,最终在端口输出不同透射率的透射谱线。在微扰区折射率为1.364、耦合间距L依次为1.5985μm,1.6005μm,1.6025μm,1.6045μm,1.6065μm时,其输出端口的透射谱如图7所示。
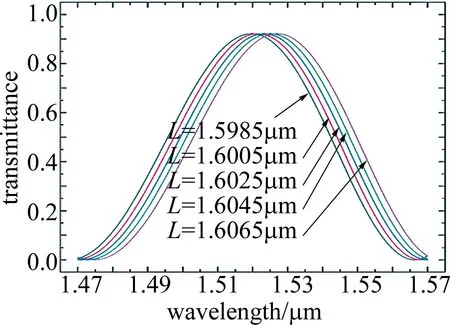
Fig.7 Output transmission spectrum at different coupling intervals
在DCPCF微扰区的耦合间距发生变化时,透射峰发生移动,随耦合间距的逐渐增大,透射峰发生红移。在该波段下,各耦合间距所对应的透射峰值坐标分别为1.520μm,1.521μm,1.523μm,1.525μm,1.527μm,半峰全宽恒定为51nm。在该耦合间距范围内,由(5)式,将Δn替换为ΔL,可确定耦合间距变化的灵敏度SL,计算得出其耦合间距的检测精度为SL=2(无量纲单位),可用于实现改变耦合间距相关的高精度压力检测。
2.4 DCPCF的温度传感分析
通过前面对耦合微扰填充区的折射率变化和耦合间距的单独分析,依次得到该结构下的传感特性,实现耦合微扰填充区中折射率和耦合间距的同时监测,可很好地用于实现高精度温度传感设计。对于填充式温度传感器而言,除温度对材料折射率的影响外,填充液体的热膨胀对传感精度也有所提升,而在大多研究中都忽略了对填充液体热膨胀特性的利用。对于该新型双芯耦合微扰型PCF,充分利用了填充材料的物理性质,在环境温度变化时,改变填充材料折射率和体积,影响纤芯有效折射率和耦合间距,实现高精度的温度传感。
根据耦合理论,折射率和耦合间距对输出功率的影响为简单的线性叠加,根据前面对折射率和耦合间距的单独分析,由(3)式和(4)式关于温度的变化关系,得知两影响因素对传感精度产生同步提升的作用。为控制检测波段在1.30μm~1.60μm左右,在温度T依次为303K,304K和305K时,入射波段为1.40μm~1.54μm左右,其透射谱线如图8所示。
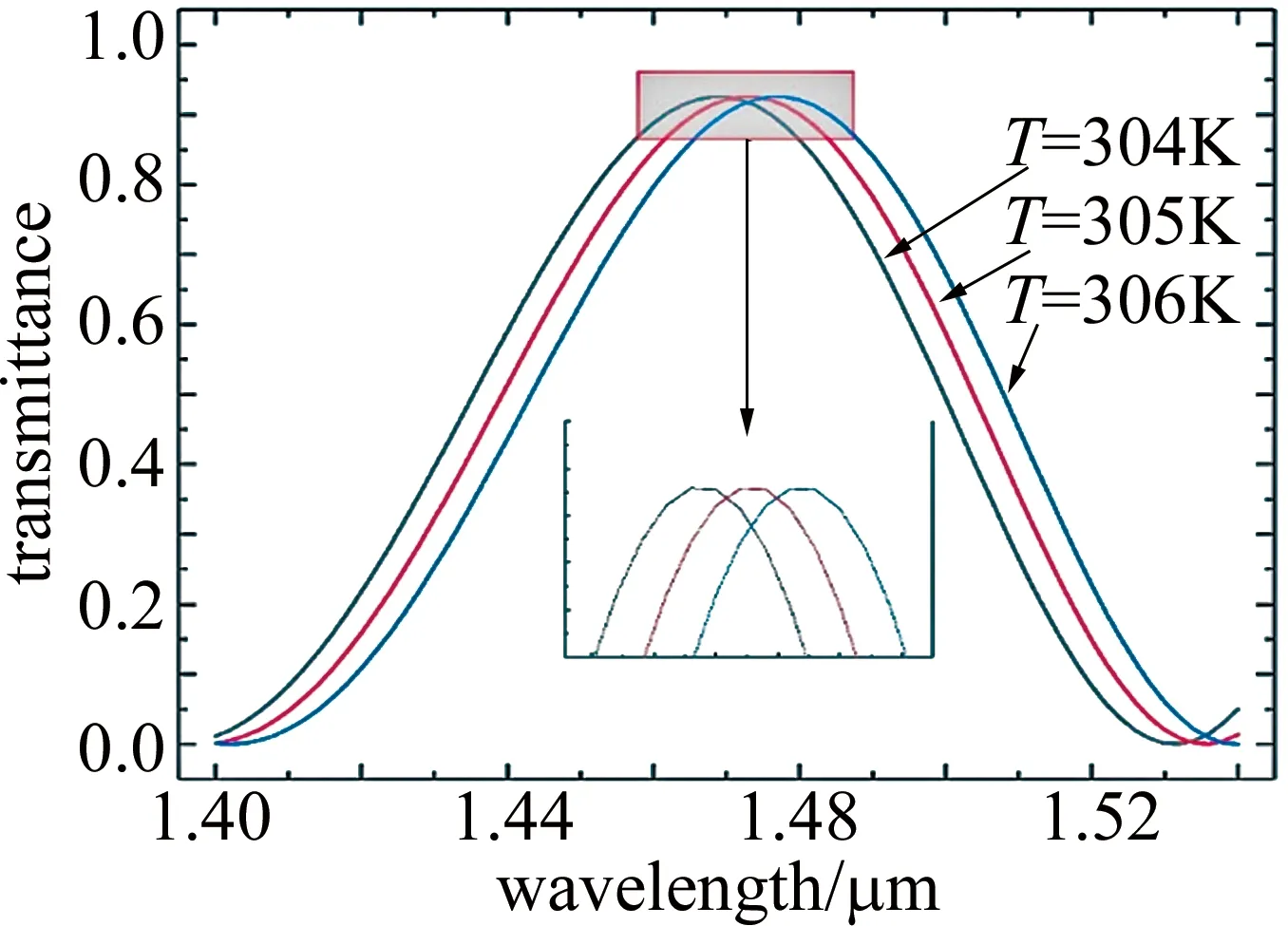
Fig.8 Transmission spectra at different temperatures
随着温度的变化,透射峰向长波长方向移动,透射峰值依次为1.468μm,1.472μm和1.476μm,其半峰全宽恒定为31nm。根据图形中的峰值移动规律,在温度较大值的增加时,该检测波段将不包含完整透射峰,且透射峰会逐渐移出该波段范围。因此,为得到最佳检测波段,实现高精度温度检测,做出如下分析。
经查阅相关实验数据,得知乙醇填充液体的温度变化范围在278K~338K左右时,具有较好的线性变化关系。由(3)式和(4)式计算可知,折射率和耦合间距满足图2所示的稳定耦合条件。通过进一步仿真分析,得到峰值移动与温度变化关系如图9所示。
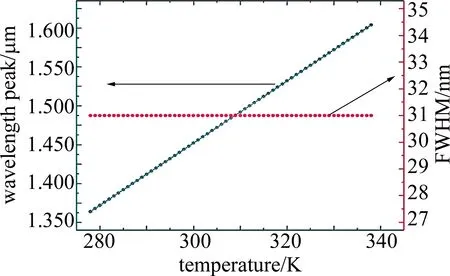
Fig.9 The relationship between transmission peak and FWHM at different temperatures
温度的变化与透射峰的移动具有很好的线性关系,对温度T(K)和透射峰值S(nm)的变化关系进行数据拟合分析,函数关系表达式S(nm)=4T(K)+256(nm),其斜率即为温度灵敏度,可达到4nm/K。半峰全宽与温度的变化关系如图9所示。根据透射峰的峰值位置和半峰全宽宽度,即可确定各温度下的输出完整透射峰所对应的检测波段,实现精准和宽温度检测的效果。
3 结 论
根据耦合理论,依次分析微扰区折射率和耦合间距对DCPCF耦合传输的影响,得出该模型能够很好地实现折射率的检测与耦合间距变化相关的内膨胀或外应力传感。根据该结构下的传输特性,针对高精度温度传感进行分析,充分利用PCF的结构特点和填充材料的物理性质,进一步提升光子晶体光纤的传感精度,实现高精度温度传感。当填充液体为乙醇时,检测温度范围为278K~338K,传感器灵敏度达4nm/K。该DCPCF传感器,根据检测环境的不同温度范围,控制波长区间出现温度细微变化的透射峰,有效分析环境温度,达到对温度的高精度实时检测的目的。该设计具有灵活性高、稳定性好和精度高等优点,同时该新型结构也有待进一步研究的价值,对实现光纤传感具有重要作用和意义。
