基于遗传算法的钢斜拉桥成桥索力优化

严松， 颜鹏飞

(中交第二公路勘察设计研究院有限公司， 湖北 武汉 430052)

钢箱梁斜拉桥主梁一般设计为自重轻、抗扭和横向抗弯刚度较大的扁平钢箱梁。与混凝土斜拉桥相比，钢箱梁斜拉桥的柔度大，耗能效果好，抗震性能好。斜拉桥设计中需要确定合理成桥状态，根据拟定的施工工序确定合理施工状态后通过各施工阶段对结构线形和内力分布进行优化和调整，使逐步趋近于合理成桥状态。钢箱梁斜拉桥恒载索力对合理成桥恒载内力状态影响很大，可在不考虑几何非线性和收缩、徐变及温度影响条件下利用斜拉索索力的可调性对成桥内力状态进行合理的调整与优化。该文依托相关工程背景，分析其初始成桥索力的确定方法，介绍基于多目标线性规划遗传算法在恒载下的成桥索力优化方法。

1 斜拉桥合理成桥状态

斜拉桥合理成桥状态是指恒载作用下成桥阶段各构件的一种理想受力状态，通常取斜拉桥主梁和主塔中弯曲应变能最小状态作为合理成桥状态，表征成桥阶段内力分布的好坏。一旦斜拉桥结构体系被确定，总能找到一组斜拉索索力，使得结构体系在确定性荷载作用下，某种反映受力性能的目标达到最优。对于中小跨度钢箱梁斜拉桥，应综合考虑成桥阶段主梁线形、主梁和主塔弯矩及应力、索力等结构状态。斜拉桥成桥主梁线形主要以施工阶段主梁立模标高控制为主，成桥阶段索力调整常以成桥设计索力控制为主，线形控制为辅。只要保证梁塔受力和成桥索力分布最优，即可达到对应的合理成桥状态。

2 初始成桥索力确定方法

单一的确定成桥索力的主要构件弯曲能量最小法并不能使成桥索力最优，但以此初始索力为后期优化前提的特定约束条件下的遗传算法可以避免索力优化结果趋于局部最优解，并最终达到理想成桥索力。

选取斜拉桥主要构件的弯曲应变能U作为优化目标函数。对于斜拉桥离散杆系结构：

(1)

式中:n为离散结构单元总数；li、Ei、Ii、Mi分别为i号单元杆件长度、弹性模量、截面抗弯惯性矩和截面弯矩。

矩阵形式表示为：

U={M}T[B]{M}

(2)

式中:{M}为弯矩向量；[B]为系数对角矩阵，对角元素为：

bii=li/(2EiIi)，i=1,2,…,n

(3)

令优化前弯矩向量为{M0}，施调向量为{ΔT}，优化后弯矩向量为{M1}，则:

{M1}={M0}+[C]{ΔT}

(4)

式中:[C]为索力对弯矩的影响矩阵，其中元素Cj为索力施调向量{ΔT}中Tj单位力值变化引起的{M1}变化量。

将式(4)代入式(2)得：

U=c0+{M0}T[B][C]{ΔT}+{ΔT}T[C]T[B]·{M0}+{ΔT}T[C]T[B][C]{ΔT}

(5)

合理成桥状态下结构弯曲应变能最小时：

∂U/∂Ti=0,i=1,2,…,m

(6)

式中:m为施调拉索组数。

将式(5)代入式(6)得：

[C]T[B][C]{ΔT}+[C]T[B]{M0}=0

(7)

求解式(7)的m阶线性方程组即得到优化前弯矩{M0}下结构弯曲应变能最小时的优化索力{T1}和对应优化弯矩{M1}。

{T1}={T0}+[A]{ΔT}

(8)

式中:[A]为索力对索力的影响矩阵，其中元素Aj为索力施调向量{ΔT}中Tj单位力值变化引起的{T1}变化量。由影响矩阵[B]和[C]的含义可知：

(9)

式中右端矩阵[δ]和[Δ]中元素δij、ΔiP写为：

(10)

将式(10)代入式(7)得：

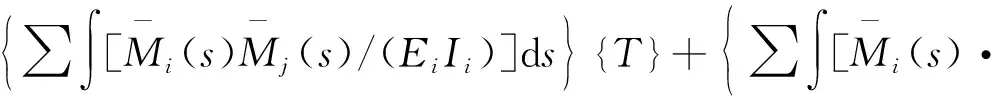
(11)

类比力法方程的形式，将上式拓展为包含弯矩项和轴力项的力法方程：

(12)

式(12)中换EiIi为ζEiIi(ζ取较小数，如0.001)，则轴力项相较于弯矩项可忽略不计，式(12)即与式(11)等同。取主梁刚度足够小时，式(11)表示全桥一次落架计算的施调索力组{T}引起的全桥基本结构[无拉索及外荷载M0(s)]弯曲应变能正好抵消调索前外荷载引起的全桥基本结构弯曲应变能。

即以合适倍数缩小斜拉桥有限元模型整体单元刚度做一次落架计算所得全桥索力为弯曲能量最小时的初始成桥索力。计算步骤为：① 确定斜拉桥结构总体布置及压重等外荷载M0(s)；② 按斜拉桥成桥状态设计参数建立平面杆系有限元模型，单元拉压刚度EiAi不变，抗弯刚度EiIi变为ζEiIi，取ζ=0.001；③ 对成桥施加自重和压重等外荷载进行一次落架线性分析；④ 反复调整压重等外荷载参数使全桥整体受力尽量合理。

3 遗传算法索力再优化

单纯追求结构弯曲应变能最小化并不能满足索力分布均匀性的要求，而索力均匀性调整势必使弯曲应变能增加。基于初始成桥索力的再优化即利用遗传算法以若干优化指标为目标函数进行索力的再调整。文中以控制截面弯矩作为约束条件，提出以索力均匀系数αi和能量变化系数β为目标函数的多目标线性规划遗传算法模型，使索力均匀性和能量变化指标最优。

取邻近3根拉索Ti-1、Ti、Ti+1定义索力均匀系数：

(13)

取调整前后弯曲能量U0、U1定义能量变化系数：

(14)

通过式(13)控制全桥索力的均匀性，其值越小越均匀;式(14)控制调整后结构弯曲应变能变化，不至于使调整后弯矩分布变得不合理。索力再优化的多目标函数和约束条件表达式分别为：

Min{Max{αi},β}

(15)

(16)

式中:{Mu}和{Md}分别为控制截面弯矩上、下限值。

遗传算法(Genetic Algorithm)作为一种复杂系统优化的自适应概率优化技术在工程优化计算上的运用前景广阔，式(15)可由基于多目标函数的Pareto遗传算法进行Matlab编程计算。

4 应力可行域

为判断得到的最终成桥索力下成桥合理状态主梁受力是否满足要求，需要进一步结合合理成桥状态下的应力可行域对主梁恒载应力进行评估。文中钢箱梁斜拉桥主梁恒载下的截面上、下缘应力的可行域通用表达式为：

(17)

式中：[Rs]为主梁上、下缘钢板屈服应力；δy为成桥索力对主梁截面的法向应力；δhmin和δhmax分别为可变作用组合下主梁应力包络最小和最大值；δu、δd分别为恒载下主梁某截面容许应力上、下限值，且截面上缘和下缘各对应一组上下限值，区间[δd,δu]即为恒载下主梁上下缘应力可行域。合理成桥状态恒载下的主梁截面上、下缘应力均在各自应力可行域的合理位置，可判别主梁受力满足要求。

5 工程应用

某双塔单索面钢箱梁斜拉桥跨径布置为(50+96+192+70) m=408 m，中心梁高3.0 m，箱梁顶板宽度29.5 m。Z4、Z5桥塔两侧分别设置9对、5对斜拉索。拉索编号和结构总体布置如图1所示。

图1 结构总体布置图(单位：m)

Midas/Civil建立的全桥有限元模型采用梁单元模拟塔、梁和墩，只受拉桁架单元模拟56根拉索，如图2所示。主墩采用弹性连接中的刚性连接模拟，并调整局部坐标。斜拉索锚固点、索塔节点与主梁节点之间均采用刚性连接，拉索锚固点设为从节点。

图2 有限元模型

根据拟定的合理挂索张拉顺序为B1、Z1/B14、Z14→B2、Z2/B13、Z13→B3、Z3/B12、Z12→B4、Z4/B11、Z11→B5、Z5/B10、Z10→B6、Z6→B7、Z7→B8、Z8→B9、Z9。在有限元模型施工阶段中按照以上张拉顺序设置每根拉索施加单位力(1 kN)为一个独立工况，施工分析控制中索力以添加方式施加，计算完成即可整理提取出索力对弯矩的影响矩阵[C]、索力对索力的影响矩阵[A]。文中索力优化方法借助Matlab与Midas/Civil配合计算，Midas/Civil计算得到的初始成桥索力作为Matlab遗传算法的初始种群，从得到的Pareto解集中优选一组索力优化结果作为最终成桥索力。

6 索力再优化结果

如图3所示，两系数不能同时取得最优值，索力分布越均匀则弯曲能量变化越不合理，反之亦然。选取解集中索力均匀系数α=0.022对应的索力解为最终优化解，此时能量变化系数β约为0.921，即U1/U0≈2.51倍(图3中标★点)。

图3 Pareto解集索力均匀系数与能量变化系数发展曲线

如图4所示，初始成桥索力基本满足由近塔端至远塔端索力分布从小到大渐变的合理趋势，但索力均匀性较差，个别拉索出现不合理空载和过载现象。结合表1分析，基于遗传算法对初始索力再优化得到的最终成桥索力分布更合理，均匀系数明显减小。如图5所示，索力均匀性优化是以主塔和斜拉索锚固区主梁弯矩增加为代价，主梁更多地参与受力，但整体弯矩分布趋于合理。非锚固区主梁弯矩水平变化小，如Z3辅助墩最大负弯矩保持为78 000 kN·m左右。

图4 索力优化前后对比

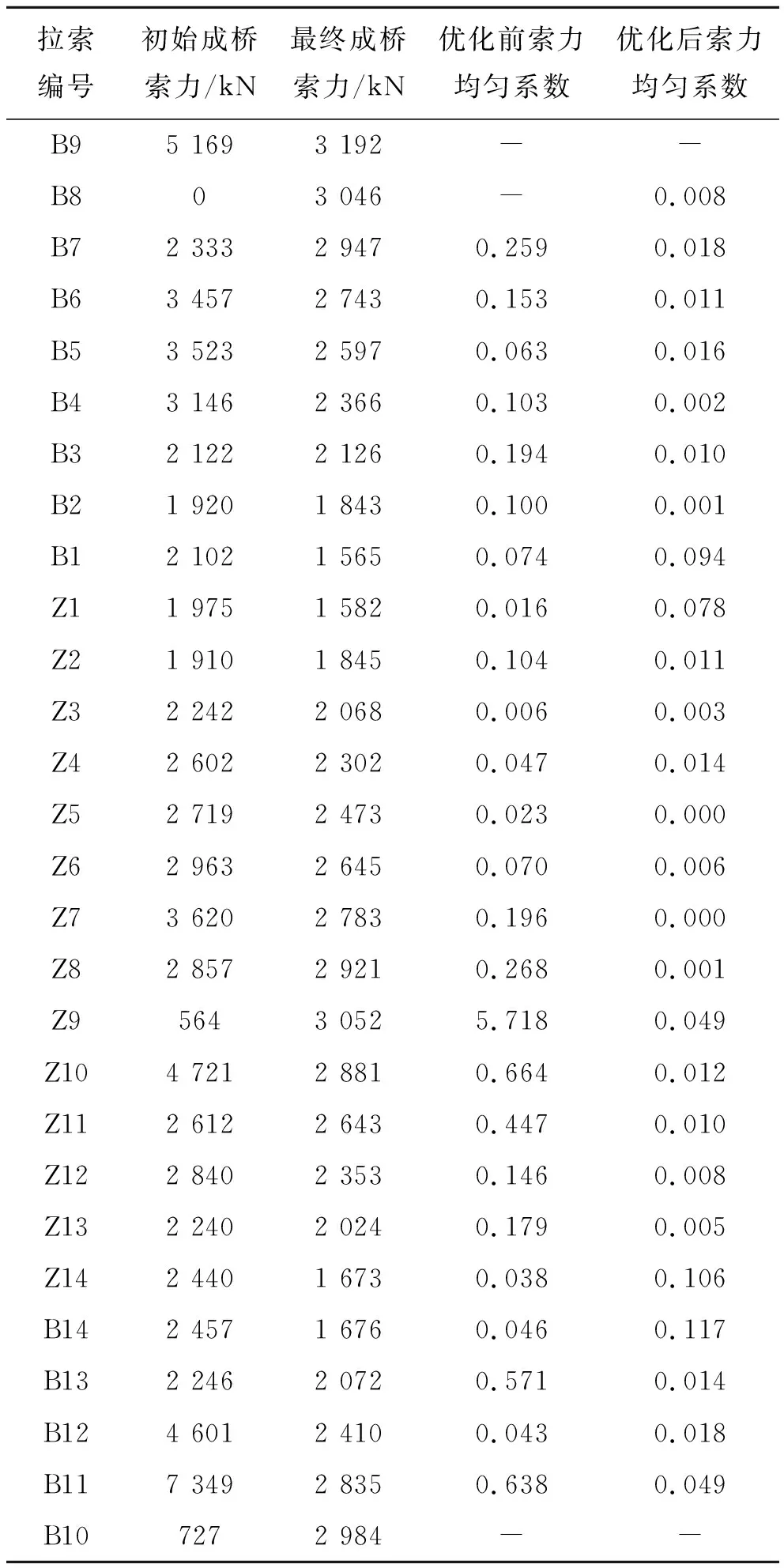
表1 索力优化结果对比

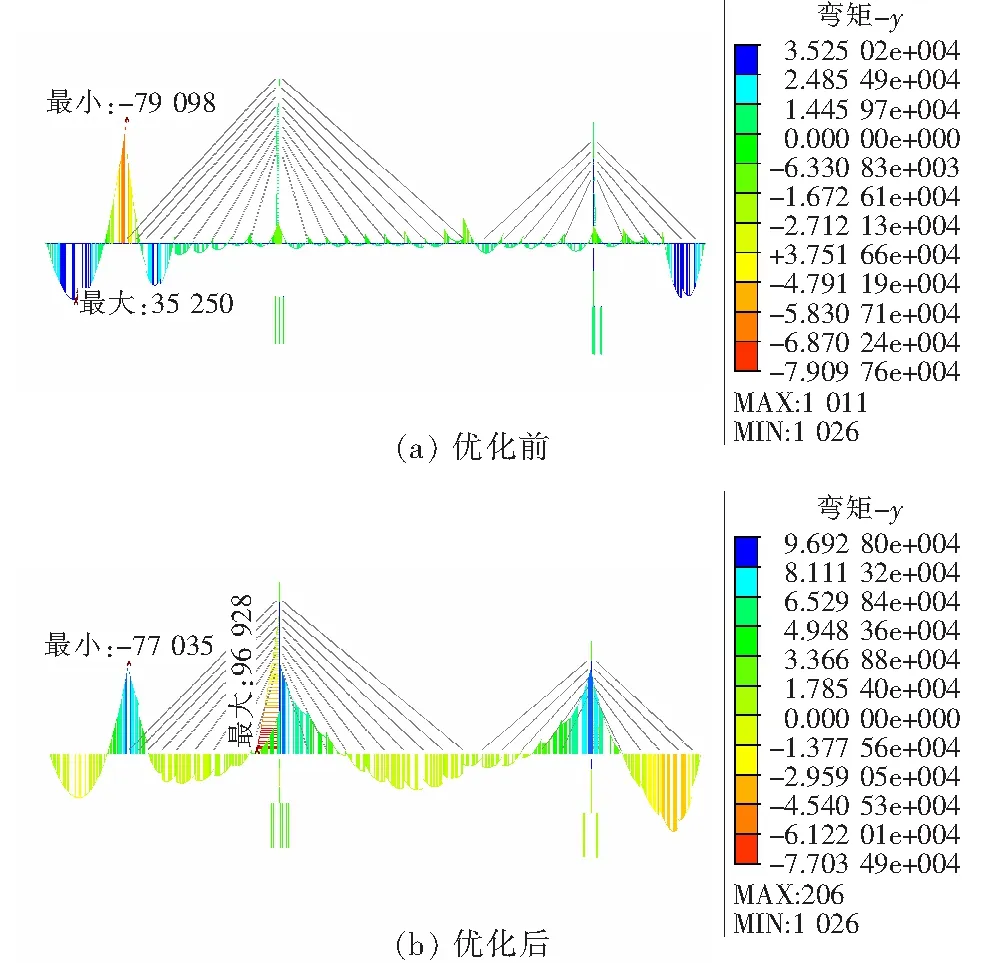
图5 索力优化前、后主梁弯矩分布(单位：kN·m)

如图6所示，最终成桥索力时主梁恒载作用下的上、下缘应力分布均居中于恒载应力可行域内，表明通过遗传算法索力再优化得到的最终合理成桥状态满足主梁合理受力的要求。

图6 合理成桥状态主梁上、下缘应力范围

7 结语

以弯曲能量最小法为分析前提，基于多目标线性规划的遗传算法对于钢斜拉桥成桥索力优化的效果理想。实例分析可知索力优化目标选取及优化效果往往取决于计算者对于具体结构的理解和优化侧重，并无绝对的方法优劣之分，需要综合分析各优化目标的效果并进行合理取舍。文中创新提出以能量法和线性规划遗传算法结合的分步算法，借助通用计算软件Matlab和Midas/Civil针对同类型斜拉桥结构的优化计算是方便可行的。该方法综合了能量法求解初始索力与遗传算法求解优化目标下成桥索力的优越性。文中阐述的中等跨径钢斜拉桥索力优化实例的方法可作为同类型斜拉桥之参考，对于较大跨径和复杂形式的斜拉桥，成桥索力优化有待进一步验证。