输电线路杆塔结构及基础系统可靠度的优化分配*

吴 静， 韩军科， 李茂华， 韩玉舟， 朱易龙， 安旭文， 侯建国

(1 中国电力科学研究院有限公司， 北京 100192； 2 武汉大学土木建筑工程学院， 武汉 430072；3 北方工程设计研究院有限公司， 石家庄 050011)

0 引言

目前，国内外对输电线路中的杆塔结构、基础、导地线等单个组件可靠度的研究较多，而将输电线路杆塔结构、基础、导线、金具及绝缘子等组件所组成的结构系统作为一个整体，研究结构系统的可靠度及其优化分配则较少。我国输电线路现场调查和分析结果表明，输电线路组件或杆塔结构子系统以及线路整体结构系统的可靠性将直接影响电网的安全运行。由于结构设计理论和设计方法的局限性，使得现有输电线路系统的整体可靠性以及防灾控制措施不够完善，有待开展深入的基础性研究。

为保障电网安全可靠供电，将输电线路看作由杆塔结构、基础、导地线、绝缘子、金具等线路元件或子系统所组成的一个结构系统，采用优化分配方法研究在一定约束条件下系统可靠度在各子系统之间的合理分配，使结构系统可靠度的匹配达到最优。结构系统可靠度的优化分配是指综合考虑各种因素，即约束条件(如经济指标、结构重量等)，用科学的决策方法，将工程设计规定的系统可靠度自上而下，从整体到局部，依次逐级进行分配，最终确定各子系统的可靠度，从而使整个结构系统的目标可靠指标得到保证[1-2]。通过结构系统可靠指标的优化分配，可以较为合理地确定各个子系统中组件的目标可靠指标，以便使各个组件在设计、加工和运行时的可靠度得到保证；可以了解各个组件可靠度、子系统可靠度与整体结构系统可靠度之间的相互关系，明确设计的主要矛盾；可以更加全面地权衡结构系统的功能要求、材料用量、费用与耐久性的关系，以期获得更加合理的结构系统设计成果，提高结构系统设计的技术质量和水平。

结构系统可靠度的分配方法总体上分为两大类，即无约束分配方法和有约束分配方法。无约束分配方法包括等分配法、AGREE分配法、评分分配法等[3]；无约束分配方法应用上较为方便，但未考虑其他约束条件的影响，与实际情况差别较大。在实际工程中，结构系统可靠度的分配必然受到各种条件的制约。在一定条件的约束下，结构系统可靠度的优化分配是全局优化问题，其核心思想是分解协调[4-6]。输电线路系统设计时，可将其视为由杆塔结构、基础、导地线、绝缘子、金具五部分组成的串联系统。基于经济指标，对输电线路结构的系统可靠度进行优化分配，可按照分解协调法的主导思想求解，即在输电线路系统设计的全局协调优化中，力求将系统可靠度合理地分配给杆塔结构、基础、导地线、绝缘子、金具子系统，使输电线路系统可靠度的匹配达到最优。

本文根据某±800kV同塔双回路输电线路的工程实例，在对输电线路杆塔结构及基础可靠度进行计算分析的基础上，建立输电线路杆塔结构、基础的成本与相应结构可靠度之间的函数关系；基于经济指标的约束条件，对输电线路杆塔结构及基础系统可靠度的优化分配进行计算分析。

1 结构系统可靠度优化分配数学模型

设输电线路系统的总成本为C0，第i个子系统的可靠度和成本分别为Psi和Ci，建立输电线路系统可靠度Ps与各子系统可靠度Psi之间的函数关系Ps=f(Psi)，各子系统可靠度Psi与其成本Ci之间的函数关系为Psi=g(Ci)，则输电线路系统基于经济指标的可靠度优化分配模型可表示为：

FindC=[C1,C2,C3,C4,C5]T

(1)

Ps=[Ps1,Ps2,Ps3,Ps4,Ps5]T

(2)

目标函数为maxPs。

约束条件为：

(3)

根据上述输电线路系统可靠度优化分配数学模型可知，基于经济指标对输电线路系统的可靠度进行优化分配时，需要建立两个函数关系式：

1)输电线路系统可靠度Ps与子系统可靠度Psi之间的函数关系为Ps=f(Psi)；2)各子系统可靠度Psi与其成本Ci之间的函数关系为Psi=g(Ci)。

由于统计数据的缺乏，目前还难以建立导地线、金具和绝缘子子系统可靠度与各自成本之间的函数关系，故本文在对输电线路系统可靠度优化分配时，只对输电线路杆塔结构和基础的可靠度进行分配。故输电线路系统可靠度优化分配的数学模型可简化为：

FindC=[CT,CJ]T

(4)

Ps=[PsT,PsJ]T

(5)

目标函数为maxPs。

约束条件为：

CT+CJ≤C0

(6)

式中：CT，CJ分别为杆塔结构和基础的成本；PsT，PsJ分别为杆塔结构和基础系统的可靠度。

2 输电线路杆塔结构及基础系统可靠度与成本的关系

2.1 输电线路杆塔结构及基础系统经济指标的确定

根据某条±800kV同塔双回路特高压直流输电线路工程量的预算指标，本文对该输电线路的总成本(不含材料运杂费及安装施工等费用)进行计算。杆塔结构采用角钢塔，角钢单价为7 500元/t，用钢量为278.9t/km，杆塔结构成本为209.18万元/km；基础混凝土和钢筋单价分别为1 000元/m3和5 000元/t，混凝土用量为321.4m3/km，钢筋(含铁件)用量为26.5t/km，杆塔基础的成本为45.39万元/km。由此可得输电线路杆塔结构和基础的成本C0=254.57万元/km。

2.2 输电线路杆塔结构可靠度与成本的关系

2.2.1 杆塔结构可靠度与结构重要性系数的关系

输电线路中直线塔所占比例较大，且直线塔对工程总成本的影响较大。本文以±800kV同塔双回路特高压直流输电线路中的直线塔SZC27102为研究对象，直线塔SZC27102的主材规格最大为Q420双拼组合角钢2L180×16，水平档距和垂直档距分别为510m和650m，呼高为66m，塔腿间距为17.54m，设计基本风速V为27m/s。

根据上述设计条件，利用直线塔SZC27102的ANSYS模型，计算杆塔结构构件的可靠度(基本变量的统计特征见文献[7])，并采用临界强度分枝-约界法研究杆塔结构的失效模式。整个杆塔结构可视为是若干失效模式组成的串联系统，而每一个失效模式又可看成是由各失效元件组成的并联系统[8]。按照文献[9-10]中给出的系统可靠度计算方法，分别取结构重要性系数γ0=1.0，1.05，1.1，1.15，1.2，1.25，1.3，1.35等，计算杆塔结构在自重+60°风向工况下的系统可靠度βT。当风荷载重现期T按100年考虑，杆塔结构可靠度βT与结构重要性系数γ0的关系如图1所示。

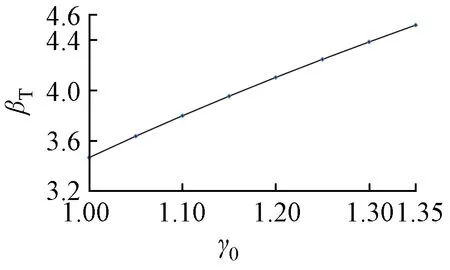
图1 βT-γ0关系曲线

对曲线进行拟合，可得风荷载重现期T=100年时，杆塔结构可靠度βT与结构重要性系数γ0之间的关系见式(7)，相应的标准差为0.016 0，相关系数为0.999 2。

βT=3.004 8γ0-0.480 7

(7)

2.2.2 杆塔结构成本增大系数-结构重要性系数模型

文献[11]经过对国内外输电线路的倒塔事故率进行比较研究，指出在小幅增加成本的前提下，适当提高某些设计荷载，可有效降低倒塔事故率。根据±800kV同塔双回路特高压直流输电线路中直线塔的设计资料，本文分别取结构重要性系数γ0=1.00，1.10，1.15，1.20，1.25和1.30，计算直线塔的材料用量或成本。参照文献[11]的研究思路，本文以γ0=1.0时直线塔的成本为基准，γ0取其他值时的杆塔成本与相应的结构重要性系数的比值定义为杆塔结构的成本增大系数αT。根据γ0取不同值时杆塔结构的材料用量计算结果，求得杆塔结构的成本增大系数αT与结构重要性系数γ0的关系见图2。

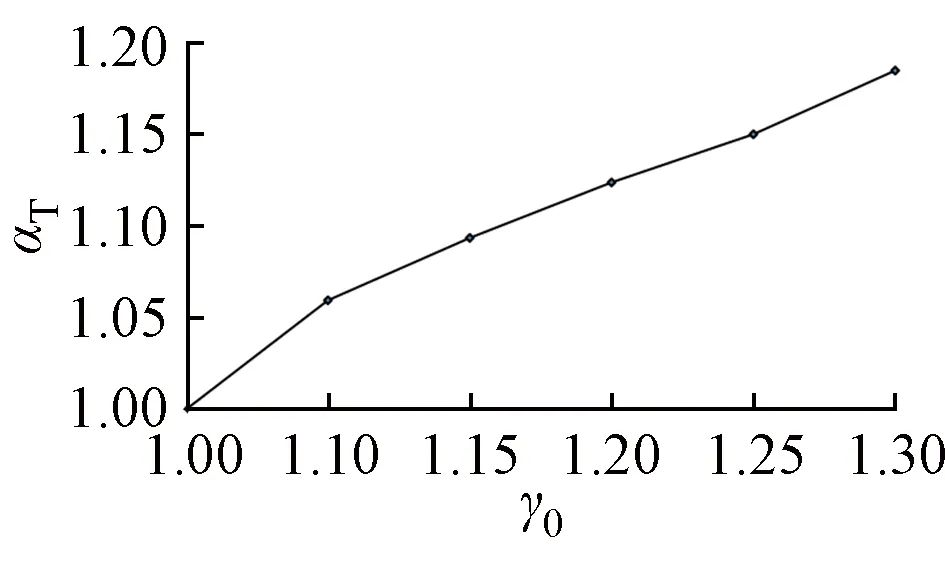
图2 αT-γ0关系曲线

经过对上述计算结果分析，同时参考文献[11]，本文建议输电线路杆塔结构的成本增大系数αT与γ0之间可采用下列拟合函数，其中标准差为0.001 1，相关系数为0.999 9：

(8)

由于钢材的费用与钢材的材料用量成线性增长，故式(8)实质上也就是杆塔结构的成本(不含运杂及安装费)增大系数αT与γ0之间的函数关系。

2.2.3 杆塔结构成本与其可靠度的关系

根据已确定的杆塔结构可靠度βT与结构重要性系数γ0之间的关系以及杆塔结构成本增大系数αT与结构重要性系数γ0之间的关系，经过变换可求得风荷载重现期T=100年时，输电线路杆塔结构的成本增大系数αT与可靠度βT之间的函数关系为：

αT=0.998 5(0.332 8βT+0.160 0)0.642 2

(9)

设γ0=1.0时杆塔结构的预期成本为C0T，γ0为其他值时，杆塔结构的成本为CT，由此确定杆塔结构的成本与其可靠度之间的函数关系为：

CT=0.998 5C0T(0.332 8βT+0.160 0)0.642 2

(10)

杆塔结构的成本C0T可按杆塔呼高66m，γ0=1.0时的计算条件确定。输电杆塔呼高为66m、结构重要性系数γ0=1.0时，考虑到螺栓、连接板等所消耗的钢材，杆塔结构用钢量为69.28t，根据工程经验，将上述计算用钢量乘以1.5的放大系数作为输电线路杆塔结构的实际用钢量，即杆塔结构的实际用钢量为1.5×69.28t=103.92t。钢材单价为0.75万元/t，故输电线路直线塔预期成本C0T=103.92×0.75=77.94万元。

2.3 输电线路杆塔基础可靠度与成本的关系

2.3.1 杆塔基础上拔稳定可靠度与结构重要性系数的关系

原状土掏挖基础、现浇钢筋混凝土基础和混凝土基础是主要的杆塔基础形式。原状土体的上拔稳定可采用剪切法计算，回填土体的上拔稳定可采用土重法计算[12]。本文基于剪切法对掏挖扩底类原状土基础的上拔稳定可靠度进行计算分析。

根据±800kV同塔双回路特高压直流输电线路中的直线塔结构在荷载作用下塔脚的内力值，基于剪切法确定基础埋置深度ht和基础底板直径D，据此计算在不同呼高及相应基础作用力下杆塔基础的上拔稳定可靠度，并选取成本最小的基础为代表，建立杆塔基础的可靠度-成本函数。当杆塔基础的附加分项系数γf=1.1时，分别取γ0=1.0，1.05，1.1，1.15，1.2，1.25，1.3，1.35，求得杆塔基础在自重+60°风向工况下的可靠度βJ。当风荷载重现期按100年考虑，杆塔基础上拔稳定的可靠度βJ与结构重要性系数γ0的关系如图3所示。

图3 βJ-γ0关系曲线

对曲线进行拟合，可得风荷载重现期T=100年，杆塔基础附加系数γf=1.1时，杆塔基础的上拔稳定可靠度βJ与结构重要性系数γ0之间的关系见式(11)，相应的标准差为0.013 1，相关系数为0.999 3。

βJ=2.630 0γ0+1.504 9

(11)

2.3.2 杆塔基础成本增大系数与结构重要性系数的关系

根据杆塔基础上拔稳定可靠度计算中所确定的基础埋置深度ht和基础底板尺寸D等，计算基础混凝土用量和钢筋(含铁件)用量，然后由2.1节所给出的基本材料单价计算杆塔基础的成本。与杆塔结构成本增大系数的计算思路相同，这里以γ0=1.0时的杆塔基础成本为基准，γ0取其他值时的杆塔基础成本与相应的结构重要性系数的比值定义为杆塔基础的成本增大系数αJ。根据γ0取不同值时杆塔基础的成本计算结果，求得杆塔基础成本增大系数αJ与结构重要性系数γ0之间的关系曲线如图4所示。

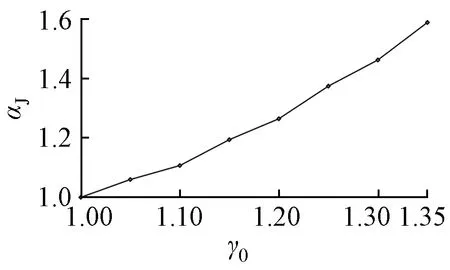
图4 αJ-γ0关系曲线

对曲线进行拟合，在不考虑运杂费时，±800kV同塔双回路特高压直流输电线路中的杆塔基础成本增大系数αJ与结构重要性系数γ0的关系见式(12)，相应的标准差为0.017 1，相关系数为0.997 0。

αJ=0.259 7e1.330 7γ0

(12)

2.3.3 杆塔基础成本与其上拔稳定可靠度的关系

根据杆塔基础上拔稳定可靠度βJ与结构重要性系数γ0之间的函数关系以及杆塔基础成本增大系数αJ与结构重要性系数γ0之间的函数关系，经变换可求得输电线路杆塔基础成本增大系数αJ与上拔稳定可靠度βJ之间的函数关系如下：

αJ=0.259 7e0.506 0βJ-0.761 4

(13)

设γ0=1.0时杆塔基础的预期成本为C0J，γ0取其他值时杆塔基础的成本为CJ，由此确定杆塔基础的成本CJ与上拔稳定可靠度βJ之间的函数关系如下：

CJ=0.259 7C0Je0.506 0βJ-0.761 4

(14)

本文在确定杆塔基础的成本C0J时，以杆塔呼高为66m，γ0=1.0的高、低腿杆塔基础的计算成本平均值3.29万元为基础，同时考虑现场实际情况的差异和基础施工引起的损耗，将上述计算成本的平均值乘以1.5的增大系数，即取杆塔基础预期成本C0J=1.5×3.29万元=4.935万元。

3 输电线路结构系统可靠度与子系统可靠度的关系

输电线路塔线结构系统可靠度的分配问题实质上就是结构系统可靠度在各个串联系统之间的分配，而对塔线结构系统可靠度进行分配首先要确定塔线结构系统可靠度与各个子系统可靠度之间的函数关系。

串联系统的可靠度可用Ditlevsen提出的窄界限法计算。当仅考虑杆塔结构和杆塔基础，即子系统数量m=2时，窄界限法计算公式可简化为：

Pf1+max(Pf2-Pf21,0)≤Pf≤Pf1+Pf2-Pf21

(15)

式中：Pf1为杆塔结构的失效概率，与杆塔结构的可靠度βT的关系为Pf1=Φ(-βT)，其中Φ(·)为标准正态分布函数；Pf2为杆塔基础的失效概率，Pf2=Φ(-βJ)；Pf21为杆塔结构和基础的联合失效概率，Pf21=Φ2(-βJ,-βT,ρ12)。

由于杆塔结构与基础的抗力是相互独立的，故在计算杆塔结构和基础的相关系数ρ12时，仅考虑杆塔结构和基础中风荷载与杆塔自重效应在标准正态空间内验算点处单位法线向量的乘积之和，即：

(16)

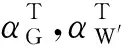
根据输电线路杆塔结构和基础可靠度计算中确定的各基本变量在验算点处的单位法线向量，由式(18)求得相关系数ρ12的取值范围在0.833～0.859之间。本文对输电线路杆塔结构及基础的系统可靠度进行分配时，取杆塔结构和基础的相关系数ρ12=0.75，0.80，0.85，0.90进行计算。

一般来说，杆塔基础的失效概率Pf2不应小于杆塔结构与杆塔基础的联合失效概率Pf21，即Pf2≥Pf21，故式(15)的左右两端是相等的，该串联系统的失效概率Pf为：

Pf=Pf1+Pf2-Pf21

(17)

因此，基于经济指标，对输电线路杆塔结构及基础系统可靠度进行优化分配时，建立相应的目标函数所需要的结构可靠概率Ps为：

Ps=1-(Pf1+Pf2-Pf21)

(18)

4 输电线路杆塔结构及基础系统可靠度的优化分配

根据本文建立的输电线路杆塔结构及基础系统可靠度的分配模型，在风荷载重现期为100年，基础附加分项系数γf取1.1时，利用遗传算法及相应的计算条件，对输电线路杆塔结构及基础系统可靠度进行优化分配。

输电线路设计中，杆塔基础的可靠度一般应大于杆塔结构的可靠度[13]。根据本文对杆塔结构和基础可靠度的计算结果和美国土木工程协会标准的建议[13]，将杆塔结构子系统的可靠度取值限制在[3.3，4.2]之间，杆塔基础的可靠度取值限制在[3.5，4.7]之间，在此范围内随机选取杆塔结构子系统和杆塔结构的初始种群。

计算中满足约束条件(式(6))的解即为可接受的解，这些解中使得目标函数(maxPs)达到最大值的解即为最优解。根据工程量的估算指标及相应材料的单价估算值，在不含运杂费及安装施工等费用时，±800kV同塔双回路直线塔中杆塔结构和基础土方工程的预期成本C0=254.57万元/km。由此求得输电线路杆塔结构及基础系统可靠度的优化分配结果，如表1所示。

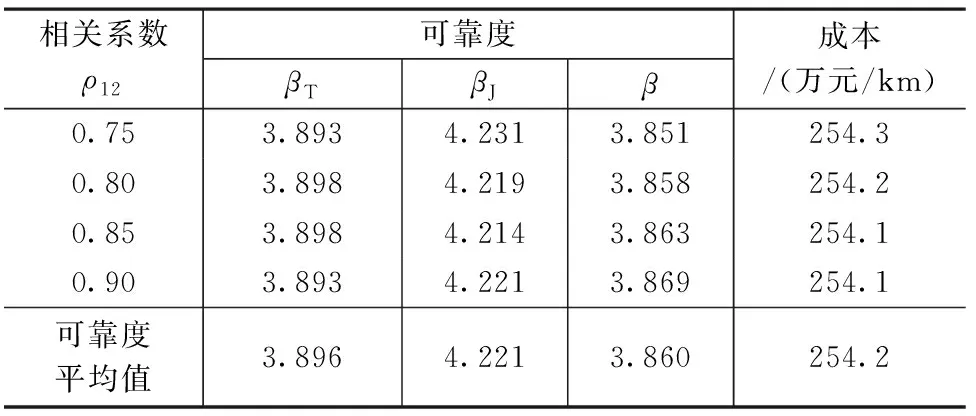
输电线路杆塔结构及基础系统可靠度的优化分配 表1

由表1可以看出：1)若以给定的成本作为约束条件，杆塔结构和基础分配的可靠度作为目标函数，当风荷载重现期为100年，γf=1.1时，在满足约束条件下，杆塔结构和基础分配的可靠度分别为3.896和4.221。若以《工程结构可靠性设计统一标准》(GB 50153—2008)[14]规定的结构构件的目标可靠度进行判断，在满足经济指标的条件下，杆塔结构分配的可靠度水平高于Ⅰ级结构发生延性破坏的目标可靠度3.7，杆塔基础分配的可靠度水平高于Ⅰ级结构发生脆性破坏的目标可靠度为4.2。相应地，输电线路系统的可靠度水平为3.860，高于Ⅰ级结构发生延性破坏的目标可靠度3.7。2)相关系数取不同值时对杆塔结构和杆塔基础子系统分配的可靠度水平影响不大。

5 结论

(1)在综合考虑输电线路杆塔结构、基础的失效模式、可靠度、结构重要性系数、成本增大系数等影响因素下，分别得到了杆塔结构、基础的可靠度-成本函数模型。

(2)建立了基于经济指标的输电线路杆塔结构及基础系统可靠度与子系统可靠度之间的函数模型，为输电线路系统可靠度的优化分配奠定了基础。

(3)±800kV同塔双回路输电线路杆塔结构及基础的系统可靠度优化分配结果表明，该工程在满足成本的约束条件下，杆塔结构和基础的可靠度分别达到3.7和4.2以上，输电线路杆塔结构及基础的系统可靠度水平亦可达到3.7以上，满足现行规范《工程结构可靠性设计统一标准》(GB 50153—2008)规定的目标可靠度的要求。