部分包覆钢-混凝土组合梁受弯承载能力及变形能力试验研究*

李 炜， 陈以一

(1 同济大学建筑设计研究院(集团)有限公司， 上海 200092； 2 同济大学土木工程学院， 上海 200092； 3 上海杉达学院， 上海 201209)

0 引言

部分包覆钢-混凝土组合构件(Partially-Encased Composite Steel and Concrete Members，简称PEC构件)由H形截面的主钢件及翼缘和腹板间填筑的混凝土组成。该截面最早由欧洲学者提出，主钢件一般采用型钢，混凝土主要用于提高主钢件的耐火能力，且截面设置了箍筋、抗剪键和纵筋(图1(a))。随着研究的深入，混凝土的加入还提高了截面的抗屈曲能力、承载力及刚度[1]。1996年，加拿大Canam公司提出一种改进形式的截面，将普通型钢替换为焊接薄壁H型钢，并在H型钢翼缘间设置连杆(Link)来改善翼缘的屈曲性能(图1(b))[2]。此截面经改进后，构造更为简单，且提高了主钢件翼缘板抗屈曲性能。

图1 部分包覆组合构件截面形式

早期连杆为一根直杆的钢筋，其两端与上下翼缘焊接。由于焊缝朝向腹板一侧施焊困难，导致焊缝质量不能保证设计承载力的要求，在试验过程中发现连杆与翼缘断开，进而导致上下翼缘失去面外的拉结约束[3]。同时，混凝土在弯剪作用下会产生斜裂缝。基于以上原因，对连杆的形式进行了改进，提出了C型与X型连杆[4]。

R Kindmann和R Bergmann[1]在1993年对12根部分包覆组合梁进行了试验研究，考察了部分组合梁的抗弯性能、抗剪性能及钢-混凝土滑移效应，同时提出了相关承载能力计算公式。结果表明：如仅考虑混凝土对钢梁翼缘屈曲的有利作用而不考虑其对承载能力的贡献，得到的计算结果偏于保守；考虑混凝土对承载力的贡献后，承载能力能高出22%～29%。

IM Assi和SM Abed等[5]在2002年对12根部分包覆组合梁进行了试验研究。将腹板两侧的混凝土替换为轻骨料混凝土，并将试验结果与填筑了普通混凝土的组合梁及纯钢梁进行了对比。结果表明：部分组合截面相比于纯钢截面，其刚度与承载力都有提高，混凝土对截面极限承载力有重要的贡献；采用轻骨料混凝土的构件自重较轻，承载力没有明显的变化。

Tremblay等[6]在2000年对11根大宽厚比带连杆的部分包覆组合柱进行了轴压试验研究。结果表明：组合柱的破坏模式为钢截面翼缘屈曲伴随着混凝土的压溃，连杆对组合柱的性能有较大影响，连杆间距增大时，组合柱延性降低，承载力在达到极值后下降迅速。

为了保证连杆与翼缘的焊接质量，高志军[7]对连杆的连接形式进行了改进。改进后的截面在翼缘板上开孔，连杆穿孔后在翼缘内外两侧焊接。试验表明这种连接形式是有效的，但加工较为复杂。

迄今为止，对部分组合结构的研究更多集中于柱，对梁的试验较少，构造参数对性能影响的研究还不充分。本文从翼缘宽厚比、混凝土类型及连杆的形式入手，研究不同参数的部分包覆组合梁在纯弯及剪弯受力状态下的单调受力性能。分析试件的承载能力，将其与理论值对比，并分析影响试件延性的相关因素。

1 试验概况

1.1 试件设计与制作

本文总结10根梁试件的试验结果。试件的总长度有两种规格，分别为1.81，1.06m，除去两侧端板各30mm及加劲段各125mm，试验段长度分别为1.5，0.75m(图2)。

图2 钢梁几何尺寸

试件采用了不同形式的连杆，分别为C型连杆及X型连杆。C型连杆即连杆弯折成槽形，通过两端的平直段与上下翼缘焊接；X型连杆则布置在上下翼缘间，呈45°布置并设置一定的平直段与翼缘焊接，连杆全长不间断。C型连杆间距与翼缘宽度之比为0.64，1.2及1.28，X型连杆间距与翼缘宽度之比为1.4。所有试件截面均在四角配置了直径为10的纵筋，纵筋两端90°弯折后焊于两侧端板上。试件几何尺寸及截面详细构造见图3与表1。

试件几何参数 表1

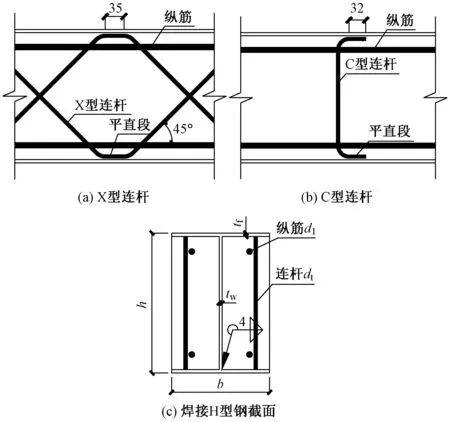
图3 试件构造

混凝土浇筑时利用主钢件作为浇筑模板，待腹板一侧混凝土凝结后再浇筑另一侧混凝土。主钢件钢材采用Q345B，钢筋采用HRB335，混凝土采用C30商品混凝土及轻骨料混凝土LC20，材料实测力学性能指标详见表2与表3。

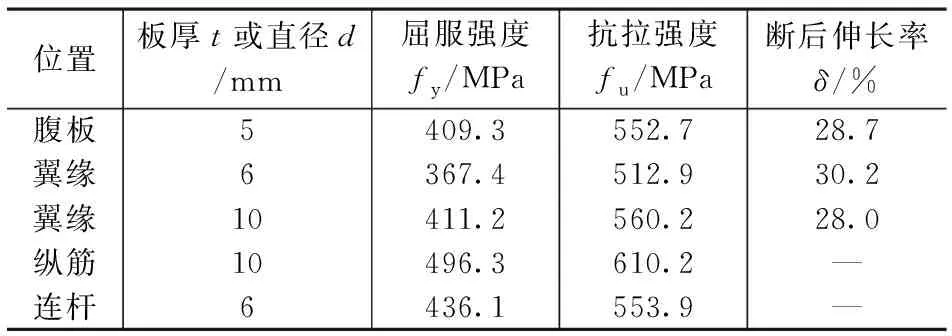
材料力学性能试验结果 表2

混凝土立方体抗压强度试验结果 表3

1.2 试验装置及加载制度

加载力学简图及试验装置图分别见图4、图5。该加载装置主要由钢柱、钢梁及液压伺服加载系统构成。两端作动器上下运动，拉动钢梁绕着钢柱顶端的销轴旋转。钢柱2的耳板上开设椭圆形孔，使钢梁2能沿水平方向适当移动。当面向装置时，定义试件表面为南面，背面为北面，右侧为东侧，左侧为西侧。图4、图5的中间水平尺寸为试验段长度(表1)加上两端加劲部分长度(图2)。

图4 加载力学简图

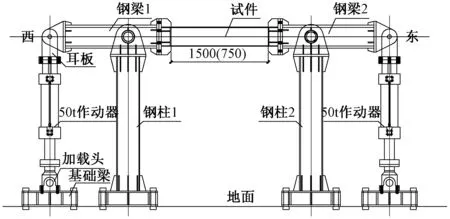
图5 试验装置图

试件采用两种不同的加载方式，即对称加载与反对称加载。对称加载时，两作动器同时施加拉力(向下)，并保持力大小相等，试件处于纯弯受力状态。反对称加载时，两作动器一拉一压(一下一上)，并保持力大小相等，试件处于剪弯受力状态，反弯点位于试件段跨中。

试验前需要计算理论屈服荷载及对应的位移，作动器在屈服荷载前采用力控制模式，到达屈服荷载后作动器改为位移控制模式并继续加载至试件破坏[9]。本试验装置下，试件试验段端部弯矩M与作动器荷载F之间的关系为如下：

对称加载时：

M=1.015F

(1)

反对称加载、试验段长为1.5m时：

M=0.583F

(2)

反对称加载、试验段长为0.75m时：

M=0.409F

(3)

1.3 测试内容

本试验通过测量试件位移来反算试件转角。试件位移计的布置如图6(a)所示。试件应变片的布置图如图6(b)所示，其中B代表主钢件上下翼缘处的应变片，S代表连杆及钢筋上的应变片，连杆的应变片布置在截面高度中心处。括号内代表试件背面相应位置的测点编号。

图6 测点布置图

2 试验结果与分析

2.1 试验现象与破坏模式

CS-5C-D试件弯矩达到32.5kN·m时，试件西侧北面观察到了混凝土竖向裂缝，紧接着试件两端及南面陆续观察到了裂缝，裂缝不断密集；弯矩达到78.2kN·m后，裂缝逐渐变长，且宽度变宽；弯矩达到108.6kN·m时，应变片数值显示受拉翼缘达到屈服；弯矩达到134kN·m时，受压翼缘屈服；弯矩达到139kN·m时，初步判断试件已经屈服。在该级荷载之前，未发现混凝土有压溃迹象，主钢件的翼缘也未屈曲，混凝土裂缝以竖向裂缝为主。

将作动器改为位移控制模式继续加载。CS-5C-D试件弯矩达到165.5kN·m时，试件西侧北面的受压翼缘屈曲，紧接着东侧北面、西侧南面处受压翼缘陆续屈曲；弯矩达到171.5kN·m时，屈曲翼缘附近的混凝土开始压溃剥落。随着试验加载，试件变形增大，混凝土裂缝不断发展，混凝土压溃也越严重。弯矩达到180.6kN·m时，大块混凝土剥落，随后试件弯矩达到峰值(181.7kN·m)并开始下降；弯矩下降至156.3kN·m时，大面积混凝土已经剥落，翼缘鼓曲明显。由于混凝土整体性破坏，主钢件抗扭性能降低，试验后期观测到主钢件平面外的扭转。试验结束后，CS-5C-D试件情况如图7所示。

图7 CS-5C-D试件加载结束时的状况

图8为CS-5C-D试件的弯矩-转角曲线，横坐标为试验段两端转角的平均值，纵坐标为试验段两端弯矩的平均值。转角、弯矩均以正向加载时产生的转角、弯矩为正。试验后期，混凝土的损伤会引起试件刚度分布不均，位移控制模式下作动器的荷载会出现偏差。两作动器荷载偏离平均值5%时，认为试件无法达到预期的受力条件，相关曲线用虚线表示。图中两条水平线代表按边缘屈服准则计算得到的理论屈服承载力My及按全截面塑性准则计算得到的理论极限承载力Mu。理论承载力的计算方法将在第2.2节叙述。

图8 CS-5C-D试件弯矩-转角曲线图

CQ-C-D-tf10试件弯矩达到58.9kN·m时，试件西侧南面观察到了混凝土竖向裂缝，紧接着试件中部及北面陆续观察到了裂缝，裂缝不断密集；弯矩达到81.2kN·m后，裂缝逐渐变长，且宽度变宽；弯矩达到144.1kN·m时，应变片数值显示受拉翼缘达到屈服；弯矩达到160.4kN·m时，受压翼缘屈服；弯矩达到180.7kN·m时，初步判断试件已经屈服。在该级荷载之前，未发现混凝土有压溃迹象，主钢件的翼缘也未屈曲，混凝土裂缝以竖向裂缝为主。

将作动器改为位移控制模式继续加载。CQ-C-D-tf10试件弯矩达到189.8kN时，试件北面的混凝土有压溃迹象，紧接着多处出现压溃迹象，但受压翼缘并未屈曲；弯矩达到235.5kN·m时，混凝土开始剥落；直至弯矩达到250.7kN·m，西侧北面的受压翼缘屈曲，同时，组合梁发生了整体性的扭转。随着加载继续，东侧北面、西侧南面及北面跨中的受压翼缘均发生了屈曲，此阶段受压翼缘鼓曲幅度均小于翼缘宽厚比为17.21εk的试件。弯矩达到264.9kN·m后开始下降，此后跨中翼缘屈曲加剧且混凝土大面积剥落。试验结束后，CQ-C-D-tf10试件情况如图9所示，图10为CQ-C-D-tf10试件弯矩-转角曲线。

图9 CQ-C-D-tf10试件加载结束时的状况

图10 CQ-C-D-tf10试件弯矩-转角曲线图

CQ-X-F试件弯矩达到32.6kN·m时，试件西侧北面观察到了混凝土斜向裂缝，随着弯矩加载直至121.8kN·m，裂缝逐渐出现在试件两端。试件东侧的斜裂缝朝向均相同且与西侧斜裂缝的朝向相反。相比于纯弯试件较为密集的裂缝，弯剪试件的混凝土裂缝较为稀疏。弯矩达到128.3kN·m后，应变片数值显示受拉翼缘达到屈服。弯矩达到154.5kN·m时，受压翼缘屈服。弯矩达到157.4kN·m时，初步判断试件已经屈服。在该级荷载之前，未发现混凝土有压溃迹象，主钢件的翼缘也未屈曲，混凝土裂缝以斜向裂缝为主。

将作动器改为位移控制模式继续加载。CQ-X-F试件弯矩达到186.6kN·m时，试件西侧北面的受压翼缘屈曲，紧接着东侧受压翼缘陆续屈曲。相比于纯弯试件的受压翼缘在梁长范围均会发生屈曲，弯剪试件的受压翼缘仅在试件两端屈曲。翼缘屈曲的同时伴随着相邻处混凝土的压溃。弯矩达到191.2kN·m时，受拉翼缘在边缘处拉裂，弯矩也达到了峰值。随着加载继续，受拉翼缘裂缝逐渐开展至腹板附近，试验终止。试验结束后，CQ-X-F试件情况如图11所示，图12为CQ-X-F试件弯矩-转角曲线。

图11 CQ-X-F试件加载结束时的状况

图12 CQ-X-F试件弯矩-转角曲线图

DS-C-F试件弯矩达到45kN·m时，试件西侧北面观察到了混凝土斜向裂缝，随着弯矩加载直至102.3kN·m，裂缝逐渐出现在试件两端。试件东侧的斜裂缝朝向均相同且与西侧斜裂缝的朝向相反。弯矩达到115kN·m后，应变片数值显示受拉翼缘达到屈服。弯矩达到136.6kN·m时，受压翼缘屈服。弯矩达到147.2kN·m时，初步判断试件已经屈服。在该级荷载之前，未发现混凝土有压溃迹象，主钢件的翼缘也未屈曲，混凝土裂缝以斜向裂缝为主。

将作动器改为位移控制模式继续加载。DS-C-F试件弯矩达到157kN·m时，斜裂缝迅速发展并上下贯通，受压区混凝土压溃，混凝土表面也凸出主钢件宽度以外；弯矩达到172.2kN·m时，西侧北面受压翼缘屈曲，紧接着东侧受压翼缘陆续屈曲，翼缘屈曲的同时伴随着相邻处混凝土的压溃；弯矩在179.1kN·m时达到峰值并开始下降，混凝土表面凸出主钢件宽度非常明显。两端作动器荷载逐渐下降直至试验结束。试验结束后，DS-C-F试件情况如图13所示，图14为DS-C-F试件的弯矩-转角曲线。

图13 DS-C-F试件加载结束时的状况

图14 DS-C-F试件弯矩-转角曲线图

CS-C-D，CS-X-D与CQ-5-D试件的试验现象及弯矩-转角曲线与CS-5C-D试件类似，CS-X-F与CS-C-F试件的试验现象及弯矩-转角曲线与CQ-X-F试件类似，DS-X-F试件的试验现象及弯矩-转角曲线与DS-C-F试件类似。

综合各试件的试验现象及弯矩-转角曲线可知：纯弯试件受弯时，受拉区混凝土开裂，中性轴上移，受拉翼缘较受压翼缘更早屈服；当受压翼缘屈服时，试件所受弯矩已达到My；当试件所受弯矩达到Mu时，翼缘未鼓曲，混凝土也未压溃，可见混凝土提高了翼缘的屈曲承载力。对于翼缘宽厚比为17.21εk的试件，翼缘鼓曲早于混凝土压溃发生，伴随着翼缘鼓曲越加明显，混凝土压溃也更严重；翼缘宽厚比为10.30εk的试件，混凝土压溃早于翼缘鼓曲发生，混凝土严重压溃后才观察到翼缘鼓曲；当混凝土大面积剥落时，弯矩-转角曲线往往开始进入下降段。

对比不同剪跨比的剪弯试件，剪跨比为3的试件，其破坏模式仍以弯曲破坏为主，体现为试验段端截面混凝土的压溃与受压翼缘的屈曲；剪跨比为1.5的试件，其破坏模式则以弯剪破坏为主，混凝土斜裂缝贯穿截面。区别于纯弯试件的正截面裂缝，剪弯试件的裂缝以混凝土斜向裂缝为主。

2.2 试件承载能力

采用边缘屈服准则计算理论屈服承载力My时，假定混凝土与主钢件共同工作，全截面的应变分布遵守平截面假定。考虑开裂对中性轴的影响，不考虑受拉区混凝土的贡献，考虑纵筋与受压区混凝土对承载能力的贡献。钢材抗拉、抗压强度采用材性试验得到的屈服应力，混凝土抗压强度采用立方体抗压强度试验得到的抗压强度乘以0.67转换成的轴心抗压强度。边缘屈服准则截面应力见图15。

图15 边缘屈服准则截面应力图

采用全截面塑性准则计算理论屈服承载力Mu时，假定钢材与钢筋均达到各自的抗压、抗拉屈服强度，混凝土亦达到了自身的抗压强度，不计受拉区混凝土的贡献。全截面塑性准则截面应力如图16所示。

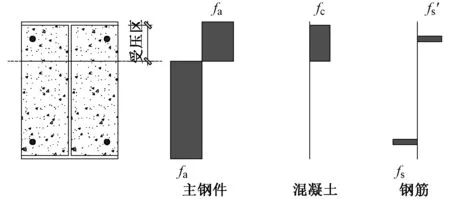
图16 全截面塑性准则截面应力图

试件实测屈服弯矩My,t可根据R.Park法(图17)从试验曲线中得到；试件实测极限弯矩Mu,t为试验实测达到的弯矩-转角曲线上的极限值，取试件两端弯矩的平均值，所得结果见表4。

图17 R.Park法确定屈服位移

试件承载能力理论值与试验值比较 表4

2.3 试件延性

采用延性系数来反映试件的塑性变形能力，其被定义为：

(4)

式中θu和θy分别代表屈服转角与极限转角，可参考R.Park法(图17)确定。由试验曲线确定峰值荷载Mmax，作水平线M=0.6Mmax交曲线于C点，连接并延长OC交水平线M=Mmax于点A。过点A做垂线交曲线于点B，B点即为等效屈服点。做水平线M=0.85Mmax交曲线于点D，D点对应的转角即为极限转角，对应的弯矩此处称为破坏弯矩。试件延性计算结果见表5。

试件延性 表5

由表5可知，部分包覆组合梁试件延性系数在9.84～21.32间，均具有较好的延性。配置了C型连杆或X型连杆的试件，延性系数没有显著区别。对比配置了不同混凝土的试件，LC20混凝土的试件延性略低于C30混凝土的试件(如CQ-5C-D试件延性略低于CS-5C-D，CQ-X-F试件延性略低于CS-X-F)，但从极限转角和延性系数两个指标看，都能支持构件发展足够的塑性变形，说明使用LC20混凝土以减轻构件自重不会影响结构安全所需的构件性能。剪跨比为3的剪弯试件，延性系数与纯弯试件接近，在10.79～13.71间；剪跨比为1.5的剪弯试件，延性系数在16.57～21.32间，其好于剪跨比为3的剪弯试件，说明混凝土剪弯破坏后，主钢件对延性开展发挥了重要作用。试验还比较了不同的翼缘宽厚比参数，宽厚比较小的试件延性比宽厚比较大的试件好。相关对比结果见表6～8。

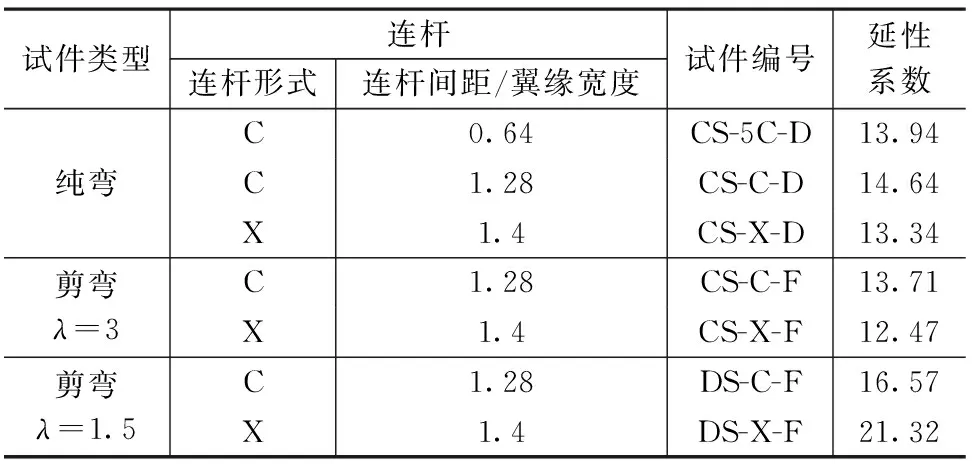
不同连杆形式试件的延性 表6

不同混凝土类型试件的延性 表7

不同翼缘宽厚比纯弯试件的延性 表8

2.4 正则化弯矩-转角曲线

对所有试件数据结果进行处理，曲线纵坐标为试件弯矩值除以边缘屈服准则下的抗弯承载力理论值；横坐标为试件转角值除以屈服转角理论值，曲线如图18所示。

图18 正则化弯矩-转角曲线图

由图18可知，所有试件的弯矩在小于屈服弯矩时表现基本一致，弯矩-转角曲线呈线性发展；采用LC20混凝土的试件(CQ-X-F与CQ-5C-D)相比于采用C30混凝土的试件，弯矩-转角曲线较早进入下降段；翼缘宽厚比为10.30εk的试件相比于翼缘宽厚比为17.21εk的试件，弯矩-转角曲线较晚进入下降段。配置了不同连杆形式的试件，在其余参数相同的情况下，由于混凝土损伤的随机性，弯矩-转角曲线有所区别，但基本类似。

3 结论

(1)混凝土的引入不仅能提高翼缘板的屈曲承载力，还能提高构件的承载能力。在本试验翼缘宽厚比的范围内(表1)，翼缘在达到理论极限承载力Mu前没有发生屈曲。混凝土严重剥落后，试件承载力下降。

(2)试件屈服荷载与按边缘屈服准则计算得到的理论屈服承载力My的比值在1.01～1.4间，与计算值较为吻合；试件极限荷载与按全截面塑性准则计算得到的理论极限承载力Mu的比值在1.15～1.36间。

(3)本试验中连杆间距与翼缘宽度的比值为0.64，1.28及1.4，相同受力条件下的试件延性基本处于同一水平；采用LC20混凝土的试件延性虽然比采用C30混凝土的试件延性低，但仍有较高延性；翼缘宽厚比较小的试件延性比宽厚比较大的试件好。本试验中部分包覆钢-混凝土组合梁延性系数为9.84～21.32，具有良好的变形性能。