软弱地层对狭长深基坑变形的影响研究

赵 宇，范存新，郭 兵，田德新，刘得俊

（1、苏州科技大学土木工程学院 江苏苏州215011；2、中铁十六局集团有限公司 江苏昆山215334）

0 引言

随着我国城市化的快速发展，城市对于轨道交通的需求也越来越大，因此近年来各个城市间开始建设大量的地铁车站来满足人们对出行的需求［1-2］。地铁车站大多位于城市主干道，周边存在众多房屋建筑与地下管线，一旦基坑开挖发生事故，就会造成周边环境破坏；特别是在软土地区的基坑开挖，由于软土的强度低、扰动性大等特性，开挖施工常常会使围护结构产生较大变形，所以对处于深厚软土层中的狭长深基坑进行研究具有一定的工程意义［3］。

目前大量学者针对软土深基坑变形进行了分析研究，王立忠等人［4］采用MMSD 法成功预测了狭长软土深基坑的基坑安全度与支护位移；张燕书等人［5］采用Midas 软件，研究了软土层对狭长深基坑地表沉降的影响，并得到相关规律；唐寅伟［6］使用Flac 3D软件，对苏州地区超深地连墙施工引起的土体变形进行了分析总结。李福林［7］通过Plaxis 3D 软件，发现狭长深基坑开挖深度对基坑侧壁土体竖向位移有较大影响。

从上述研究可发现，根据工程实际情况，并采用有限元模型进行进一步分析基坑变形情况，是目前的一种普遍方法。通过收集苏州地区实际工程项目［8-11］资料，得知苏州地区地下软土层厚度及基坑开挖深度变化普遍较大，软土层厚度一般为1.4～20.0 m，基坑开挖深度一般为13.0～24.0 m。考虑到基坑工程具有较大区域性，基坑开挖深度、软土层厚度、软土参数等因素的变化会导致基坑变形有所差异，为了能够对苏州深厚软土地区狭长深基坑变形规律提供工程参考，本文以苏州地区某地铁车站狭长深基坑为工程背景进行研究。车站基坑所处软土层普遍较厚，平均厚度近20.0 m，能够较好地反映深厚软土地区狭长深基坑的变形规律，同时将实际的监测数据与有限元模拟结果进行对比分析，验证有限元模型的可靠性。最后，建立考虑渗流-应力耦合的三维地铁狭长深基坑开挖的有限元模型，通过改变开挖深度、软土层厚度及软土层倾斜角度3 个参数，分析深厚软弱土层狭长深基坑的变形规律，为后续类似工程提供科学依据。

1 有限元模型建立

1.1 工程概况

本车站为岛式站台车站，基坑采用地下连续墙与内支撑的围护方案，地下连续墙厚度为800 mm。车站基坑标准段宽度为20.7 m，开挖深度约为14.7 m，端头井宽度为25.4 m，开挖深度约为16.3 m。基坑内支撑共有5 层，第1 层为钢筋混凝土支撑，截面尺寸为800 mm×1 000 mm；标准段第3层为φ800@16钢支撑，第2、4、5层为φ609@16钢支撑，支撑间距从上至下分别为3.1 m、3.0 m、3.0 m、3.1 m 及3.445 m。端头井第3、4 层均为φ800@16 钢支撑，第2、5 层为φ609@16 钢支撑，支撑间距从上至下分别3.1 m、3.0 m、4.0 m、3.7 m 及3.4 m。根据文献［12］中说明坑外地表沉降预估曲线影响范围为4 倍开挖深度，因此选用模型宽度为120 m，长度为400 m，深度为66.9 m。车站基坑位于道路交叉口，北侧为医疗城，南侧为某大厦，地下存在多条市政管线，环境较为复杂。

1.2 有限元数值模拟

采用岩土领域通用的有限元分析软件Midas GTS NX 建立模型，模拟该车站基坑的开挖过程，将其模拟结果与实际结果进行对比，验证材料属性、围护结构变形等符合实际情况。施工工况根据实际情况进行建模，每层开挖前先进行降水，开挖结束后立即增设支撑，共计15个施工工况。土体参数根据勘察报告中的土体物理力学指标建议值和钻孔资料取值，地层分布如表1所示。

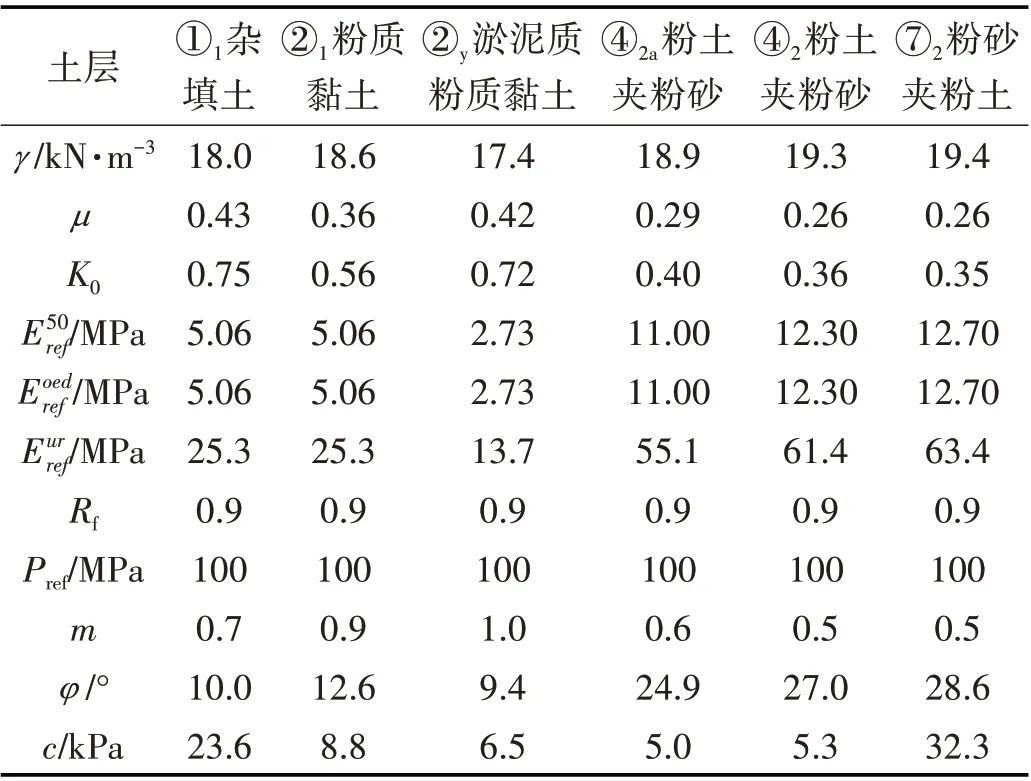
表1 场地土层物理性质Tab.1 Physical and Mechanical Properties of the Soil

模型中土体采用修正莫尔-库伦本构模型；地连墙采用2D 板单元，材料为C35 混凝土，弹性模量取值为31.5 GPa，泊松比为0.22。支撑采用1D 梁单元，钢支撑材料为Q235 钢材，弹性模量取值为20.5 GPa，泊松比为0.30；钢筋混凝土支撑材料为C30混凝土，弹性模量取值为31.5 GPa，泊松比为0.22。支撑结构均为弹性本构。通过软件的界面助手生成无厚度的界面单元来模拟地连墙与土体之间的接触面。模型四周采用法向约束，底部采用固定约束。

1.3 监测数据与模拟结果的对比分析

基坑监测平面如图1 所示，为了说明数值模型的可行性，选取3个典型的监测点06、09、12，将3处地连墙侧移与地表沉降的数值模拟结果与实测结果相对比。从地连墙侧移随深度变化曲线（见图2），地连墙侧移模拟结果与实测结果整体吻合较好，基坑变形模式均为抛物线型。模拟结果中地连墙底部踢脚普遍大于实测结果，这可能是模拟时采用的坑底土体参数低于实际土体参数所导致。在不同工况下，模拟结果中最大地连墙侧移变形位置均位于开挖面以下2～3 m，与实测结果类似。在开挖第3、4层时地连墙位移普遍增长明显，为软土强度较低、被动区土压力不足所导致。总体上来看，模拟结果可以较好地反映狭长软土基坑开挖引起的地连墙侧移变形规律。

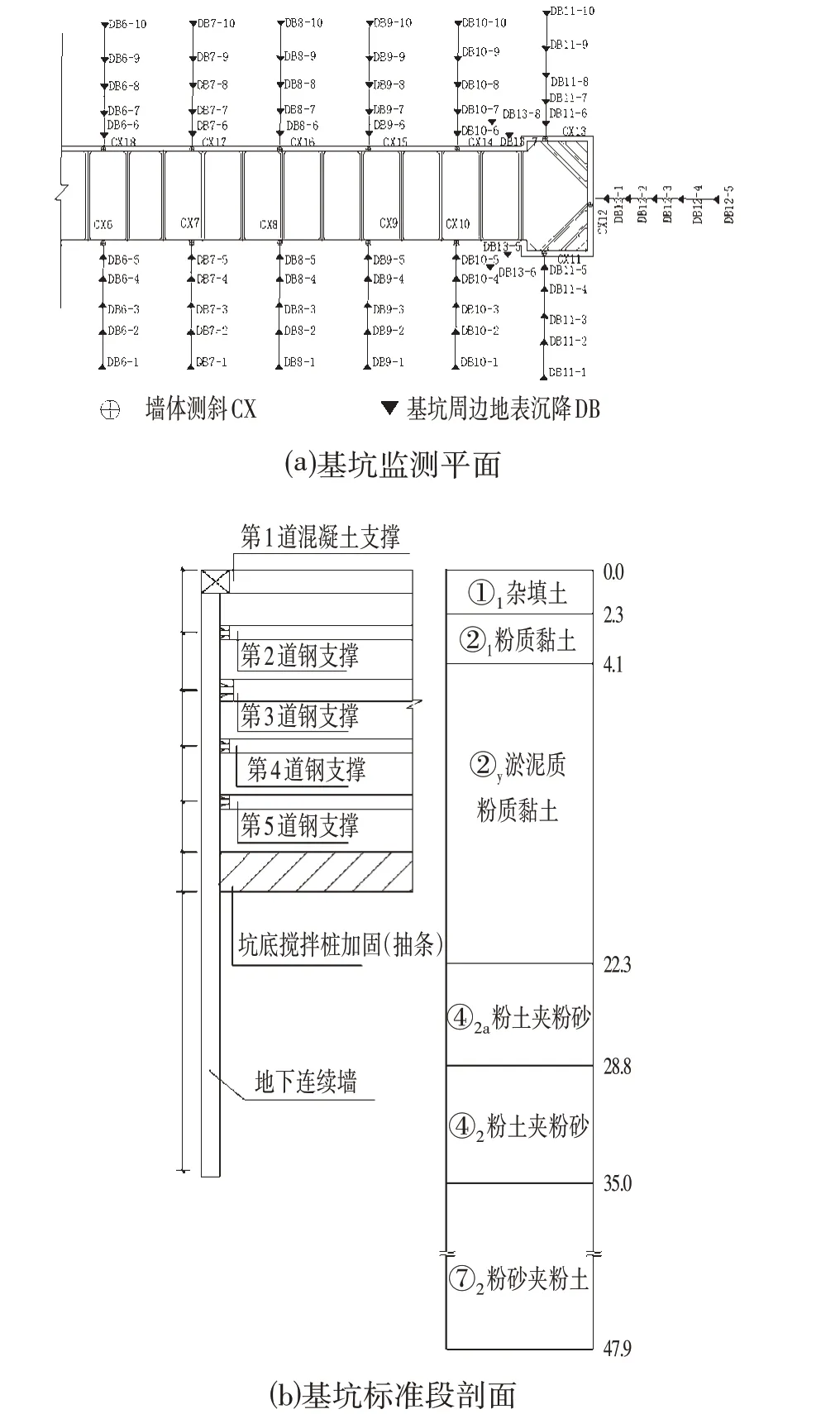
图1 基坑示意图Fig.1 Diagram of Foundation Pit

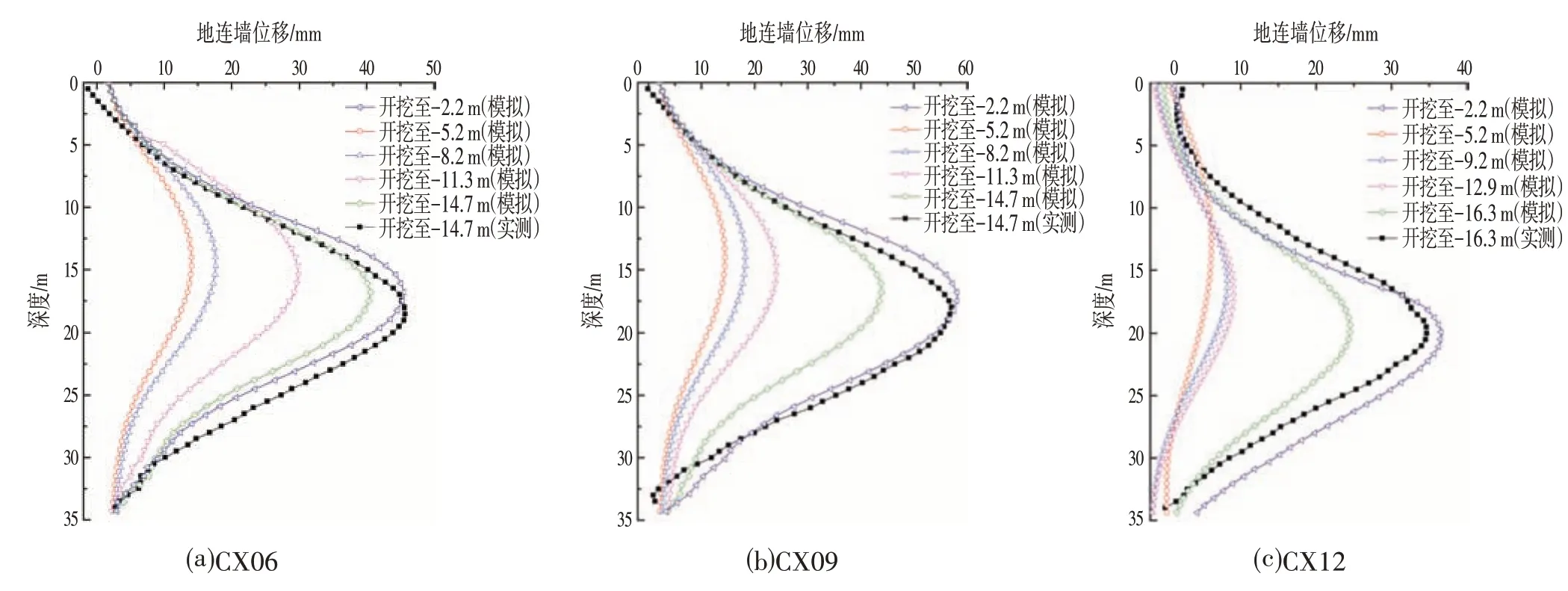
图2 地连墙侧移随深度的变化曲线Fig.2 Variation Curve of Lateral Displacement of Diaphragm Wall with Depth

从地表沉降随距墙后距离变化曲线（见图3）可看出地表沉降模拟结果趋势与实际结果均呈“凹槽型”分布形式，基坑开挖深度越深，地表沉降越大。墙后地表最大沉降位置位于0.34He～0.61He之间，超过2He后沉降逐渐趋于稳定，与实测结果相似。综合来看，模拟结果可以合理地预测地表沉降规律。

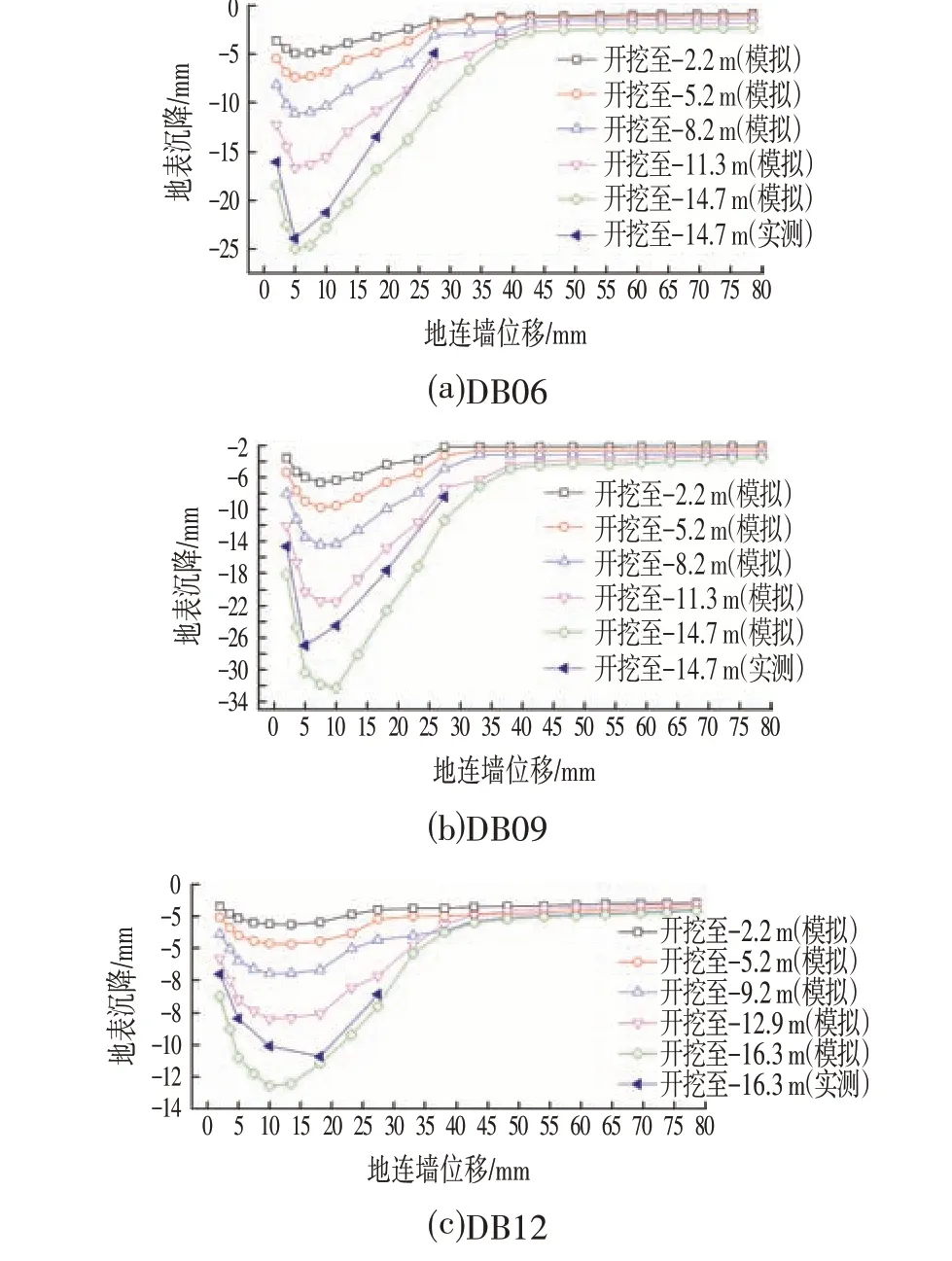
图3 地表沉降随距墙后距离变化曲线Fig.3 Curve of Surface Settlement with Sistance from behind the Wall

根据上述结果分析，地连墙侧移与坑外地表沉降模拟结果与实测结果均吻合较好，说明采用Midas GTS NX 有限元软件可以较好地模拟深厚软土狭长基坑的变形特点与趋势，同时也表明土体与围护结构参数具有一定的合理性。

2 分析模型建立

为了保证计算精度的同时，减少模型的计算时间，根据文献［13］中平面应变比PSR 的概念，将三维模型简化为平面应变模型。使用的平面应变模型尺寸为220 m×24 m×72 m。模型首层填土厚度为2 m，基坑开挖宽度为21 m，开挖深度分别为15 m、18 m、21 m。支撑形式为首层钢筋混凝土支撑，其余均为φ609@16的钢支撑，支撑水平间距为3 m。计算模型与有限元模型如图4、图5 所示。由于同一场地存在不同厚度的软土层且软土层分布并不均匀，因此本文定义软土层倾斜角度Ht来反映软土层的不均匀程度，Ht越大，软土层分布越不均匀；Ht越小，软土层分布则越均匀。模型中土体参数的取值如表2所示。

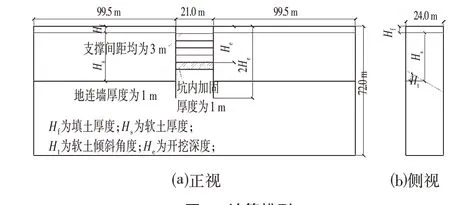
图4 计算模型Fig.4 Calculation Model

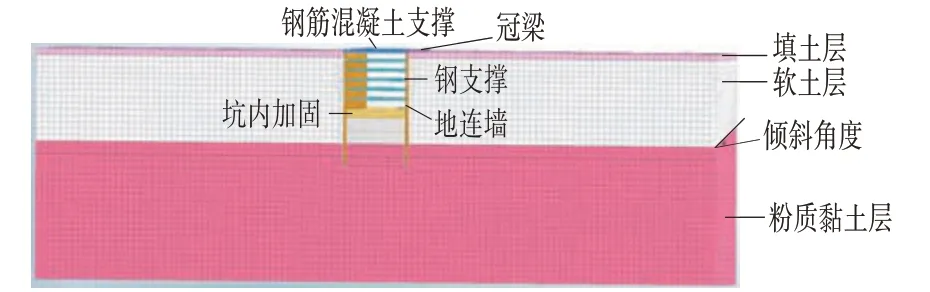
图5 有限元模型Fig.5 Finite Element Model

3 分析结果对比

根据表3 中不同软土参数得到的不同基坑变形，进行统计分析得到以下结论。

表2 计算模型土体参数Tab.2 Calculation Model Soil Parameters

表3 参数组合分析Tab.3 Parameter Analysis

3.1 开挖深度He对地连墙最大水平位移δ hm的影响

开挖深度He和地连墙最大水平位移δhm之间的关系曲线如图6所示，从图6中可以发现：

⑴当倾斜角度Ht为0°～4.76°时，随着开挖深度He与软土层厚度Hs增加，地连墙最大水平位移δhm逐渐增大，且增长的幅度越来越大。产生该现象的原因是由于基坑开挖深度与软土层厚度的增加，主动区土压力随两者的增大而增大，最终导致地连墙水平位移偏大。

⑵当倾斜角度Ht为9.46°～14.04°时，随着开挖深度He的增加，地连墙最大水平位移δhm趋势变为先增大后减小。这说明随着倾斜角度的增加，土压力分布发生变化，使得地连墙受力情况出现差异，在不同软土层厚度下，当He=18 m，地连墙最大水平位移均为最大值。

⑶随着倾斜角度Ht的增加，地连墙最大水平位移δhm均有不同程度的增加。当软土层厚度在12 m以下时，随着软土层厚度的增加，地连墙最大水平位移增长速率较小，影响较小；软土层厚度大于12 m后，随着软土层厚度的增加，增长速度逐渐增大，影响较大。

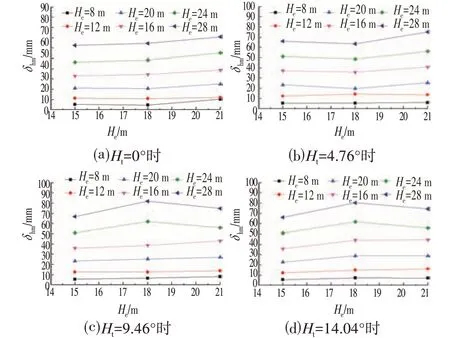
图6 不同倾斜角度Ht下He和δhm之间的关系Fig.6 The Relationship between He and δhm at Different Tilt Angles Ht

3.2 软土层倾斜角度Ht对地连墙最大水平位移δ hm的影响

将不同倾斜角度Ht下相对地连墙水最大平位移δhm/He和相对软土层厚度Hs/He的关系进行曲线拟合（见图7），可以发现它们呈明显的指数相关，拟合的曲线如下所示：

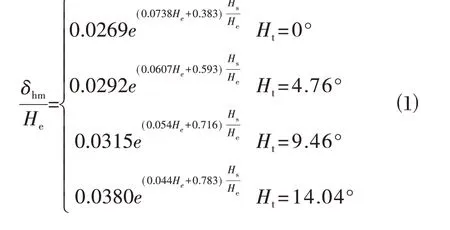
由图7和拟合关系式可以发现：

⑴随着相对软土层厚度Hs/He的增长，最大地连墙水平位移δhm呈指数增长，说明Hs对δhm有较大影响，与前文结论相同。

⑵软土层倾斜角度Ht越大，数据离散程度越小，数据点越收缩，这说明Ht较大时，开挖对δhm的影响开始减弱。当倾斜角度较小时，数据离散程度越大，开挖深度对δhm的影响也就相对较大，这时考虑软土厚度与软土层倾斜角度的同时应该考虑开挖深度对围护结构最大水平位移的影响。

⑶当遇到相似狭长软土深基坑时，可以根据软土层厚度Hs，开挖深度He，倾斜角度Ht对地连墙最大水平位移进行估算，对实际工程有一定参考意义。

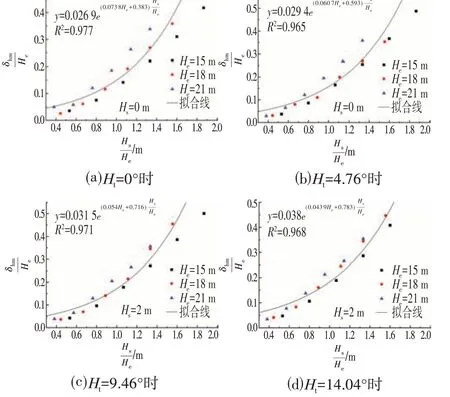
图7 不同开挖深度下相对软土层厚度Hs/He与相对地连墙最大水平位移δhm/He之间的关系Fig.7 The Relationship between the Relative Soft Soil Thickness Hs/He and the Maximum Horizontal Displacement δhm/He of the Opposite Underground Diaphragm Wall at Different Excavation Depths

3.3 开挖深度He对墙体最大水平位移深度Hw的影响

⑴由图8可以发现，随着软土层厚度Hs的增加，地连墙最大水平位移深度Hw在逐渐下移，软土层厚度较小时，地连墙最大水平位移的位置基本保持不变。这表明软土层厚度变化对地连墙最大水平位移的位置有较大影响。

⑵不同开挖深度He情况下，地连墙最大水平位移深度Hw差别不大，说明开挖深度对其影响较小。

⑶不同倾斜角度Ht下，地连墙最大水平位移深度Hw在前期差别不大，但在后期，随着倾斜角度的增加，最大水平位移位置有小幅增加。这表明倾斜角度对地连墙最大水平位移的位置有一定影响。

4 结论

本文通过工程项目实测结果对Midas GTS NX 建立的数值模型进行模型验证，并通过不同软土层厚度、倾斜角度、开挖深度3个方面来研究软土地区狭长深基坑的变形规律，得出以下结论：

⑴本文建立的苏州某车站基坑数值模拟结果与实测结果有较好的吻合度，说明采用Midas GTS NX建立的数值模型，能够较好地模拟在深厚软土地区狭长深基坑的变形特点。

⑵在软土地区，相对于基坑开挖深度与土体倾斜度，软土层厚度对基坑围护结构的变形影响较大，随着软土层厚度的增加，围护结构的最大水平位移呈指数型增长。当倾斜角度在14.04°以内时，随着倾斜角度的增加，开挖深度对围护结构水平变形的影响开始逐渐减弱。

⑶根据不同软弱土层参数下数值模拟的结果，给出了不同Ht和He条件下δhm/He和Hs/He之间的拟合公式，为后续类似工程提供参考。

⑷当基坑开挖深度变大后（18～21 m），同时软土层厚度较小时，地连墙最大侧移深度基本不随倾斜角度的变化。当基坑开挖深度较小（15 m）时，地连墙最大侧移深度变化与软土层厚度与软土层倾斜角度关联度较大，与开挖深度关联度较小。