非饱和重塑黄土应变控制等应力比试验三维离散元分析
2021-05-13蒋明镜李立青
李 涛,蒋明镜,李立青
(1.中国民航大学 机场学院, 天津 300300; 2.天津大学 建筑工程学院, 天津 300072)
黄土主要分布在干旱和半干旱地区,黄土工程中遇到的土体多处于非饱和状态,非饱和黄土试验和理论研究一直是岩土工程界的热门课题之一[1-3]。非饱和黄土的试验研究主要针对等向压缩、侧限压缩、常规三轴和真三轴应力路径等[4-7],但实际工程中如黄土路基和填方工程[8]可能出现小主应力和大主应力共同增加的等应力比路径[9]。在等应力比路径下,随着应力比的变化,土体可能发生压缩控制和剪切控制的转换,难以通过常见应力路径试验反映,因此,有学者通过等应力比路径研究黄土的力学性质并应用到本构模型研究[9-11]。
黄土宏观力学性质与其微观特性密不可分。为了研究黄土宏观力学特性的微观机制,不少学者开展扫描电镜观测、X射线计算机断层扫描[12]等微观试验。为了分析微观试验难以全面获取的接触方向、接触力等统计信息,Jiang等[13]采用二维离散单元法(DEM),使用简单胶结接触模型模拟黄土粒间胶结,研究了等应力比路径下黄土的力学特性。由于应力加载进行高应力比压缩试验难以反映理想塑性和软化,模拟采用完备的非饱和重塑黄土三维接触模型[14],对非饱和重塑黄土离散元试样开展了不同应力比的应变加载等吸力等应力比试验,研究了黄土数值试样的应力、变形及其对应的微观力学性质(平均配位情况、接触法向和接触力组构等)。
1 黄土接触模型及其微观参数
黄土颗粒/团粒形状不规则,表面附着细小黏土颗粒,在粒间接触上表现出抗弯和抗扭能力,研究采用的黄土接触模型[14],基于Jiang等[15]的完整接触模型,同时采用粒间引力考虑颗粒间的范德华力和毛细力作用。接触模型已应用于非饱和黄土三轴试验[16]和一维压缩试验[17]离散元数值分析。
假设颗粒间通过圆形截面接触,接触半径为[15]:
Rc=βR
(1)
式中:β为接触半径系数,R=2R1R2/(R1+R2),R1和R2为两颗粒半径。考虑粒间引力时,颗粒间力和弯矩的计算示意图如图1所示。接触刚度可由颗粒等效模量和颗粒法切向刚度比计算。

图1 接触模型力学响应示意图

(2)
(3)
(4)
式中:Fn为法向接触力;Fa为粒间引力;μ为粒间摩擦系数;ζc为颗粒局部压碎系数,可取ζc=2.1。
接触模型参数如表1所示。粒间引力是影响非饱和重塑黄土宏观力学性质的主要微观变量之一,对于非饱和黄土,范德华力与毛细力相比很小,粒间引力主要是由毛细水引起。粒间引力为[14]:
(5)
式中:d50为中值粒径;s为基质吸力;σv为范德华力系数;ξa,ast和bst为拟合参数,ast=ca1exp(ca2e0),e0为试样的初始孔隙比。

表1 离散元模拟微观参数[14]
2 数值试样制备与离散元实施
采用分层欠压法分五层制备黄土离散元试样,颗粒数目为42 180个,粒径级配曲线如图2所示,中值粒径d50为20 μm。为了制备大孔隙比黄土数值试样,在制样过程中施加范德华力,大小按下式计算:
(6)
式中:σv取4 kPa。试样生成后在12.5 kPa竖向压力下侧限压缩稳定(预压),预压完成后孔隙比为0.934。

图2 离散元试样粒径级配曲线
预压完成后,对黄土离散元试样上下墙体分别按10/s应变率施加荷载,对四个侧墙采用伺服控制,使试样的应力比(η=q/p,p为平均应力,q为偏应力)保持不变,以实现试样的应变控制等应力比加载。应变控制对比分级荷载施加方式容易实现较高应力比下的等应力比加载,因此为本文所采用。试验过程中保持试样的基质吸力不变(100 kPa)。在数值分析过程中,随着试样调整,接触可能消失和生成,新生成接触自动施加接触模型并赋予模型参数。
3 离散元试样的宏观性质
图3给出了非饱和重塑黄土离散元试样压缩曲线,通过与室内试验结果的对比可知,在半对数坐标中,非饱和黄土孔隙比先缓慢减小,在屈服应力之后快速减小,离散元试样的压缩线趋势与室内试验[5]相同。离散元孔隙比变化数值上与室内试验差别较大,主要是因为离散元在颗粒形状、颗粒团簇破碎等方面与实际黄土颗粒不同造成的。关于应力比的影响,离散元结果表明在一定的应力比范围内(η
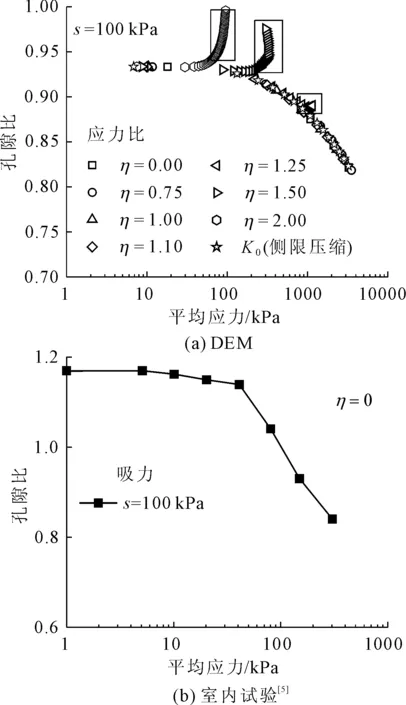
图3 等应力比压缩曲线
图4给出了非饱和重塑黄土离散元试样等应力比试验的偏应力-偏应变关系曲线,通过与室内试验结果对比可知,离散元试样的偏应力-偏应变关系与室内试验[10]结果趋势相同。在低应力比下(η
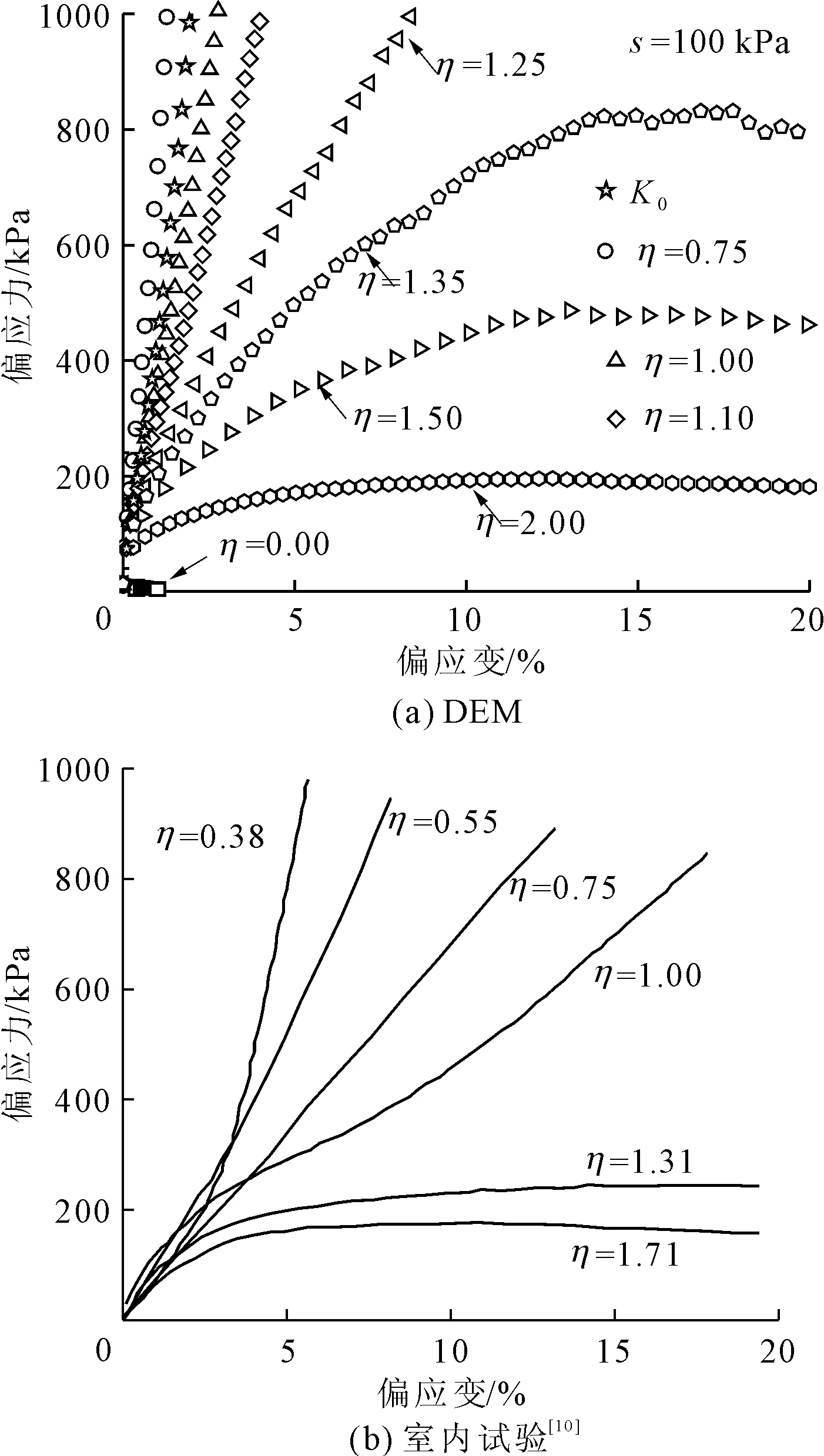
图4 应力-应变曲线
4 离散元试样的微观性质
为了探求非饱和重塑黄土宏观力学性质的微观机制,对离散元试样的配位情况和组构情况进行了分析。
平均配位数(简称“配位数”)和平均力学配位数(简称“力学配位数”)可以用来分析土体颗粒的平均接触情况,采用下式计算[18]:
Z=2Nc/Np
(7)
Zm=(2Nc-Np1)/(Np-Np1-Np0)
(8)
式中:Z为配位数;Zm为力学配位数;Nc为接触数量;Np为颗粒数量;Np0和Np1分别是接触数量为0和1的颗粒数量;Np-Np1-Np0为有效颗粒数量。
图5给出了非饱和重塑黄土离散元试样的平均配位情况,试样的力学配位数在半对数坐标系中随平均应力的增加先缓慢增加后快速增加。通过与压缩曲线的对比可知,在200 kPa平均应力以下,随着应力的增加,配位数、力学配位数、有效颗粒数量发生了较明显增加,但试样孔隙比变化较小。即试样的颗粒重排列和变形仅发生微调整,滞后于配位情况的变化。

图5 配位性质
不同应力比离散元试样的力学配位数随平均应力变化曲线保持很好的归一性,与压缩曲线表现相对应。但是配位数曲线有所不同,除等向压缩试样(η=0)外,随应力比的增加,配位数随平均应力增加的速率变大,相同平均应力下的有效颗粒数量更大。可见,虽然某平均应力下不同应力比试样的力学配位数相同,但配位情况却有一定不同,高应力比试样中有更多的颗粒参与了传力(颗粒排列调整更充分)。高应力比(η>M)试样在进入流塑阶段尾段后,有效颗粒数量接近最大,试样力学配位数基本保持不变,与之对应的,试样的孔隙比、平均应力和偏应力都基本维持不变,试样达到临界状态。可见,临界状态对应的宏微观变量都基本保持不变,且有效颗粒数量接近总颗粒数量(颗粒均参与传力),与此对应,颗粒排列经历了充分调整。
组构张量可以用来反映矢量集合方向(接触法向、接触力方向)的统计规律,组构张量计算如下[19]:
(9)
式中:ni为矢量的方向余弦。偏组构Δ可用来表示矢量集合方向的各向异性程度:
(10)
式中:F1、F2和F3是组构张量的三个不变量。
图6给出了非饱和重塑黄土离散元试样的接触方向偏组构随平均应力的变化,试样初始接触方向偏组构是原位应力状态下的偏组构(预压后),接触方向偏组构的变化明显受试验应力比的影响。随着平均应力的增加,侧限压缩试验的应力比不断下降(如图6(b)),但侧限压缩的接触方向偏组构基本保持不变(高平均应力下轻微下降)。在等应力比压缩中,η=0.00和η=0.75试样的应力比始终小于侧限压缩试验的应力比,接触方向偏组构随平均应力的增加而不断减小,应力比越小,接触方向偏组构随平均应力减小越快; 试样的应力比先是小于而后大于侧限压缩试验的应力比,接触方向偏组构随平均应力的增加先减小后增加,应力比越大,接触方向偏组构随平均应力增加越快。可见,试样接触方向偏组构的变化与其初始状态和加载应力路径关系密切。
图7给出了η=0.00和η=1.25试样接触方向组构玫瑰图(轴向为各个1°径向范围内接触的数量)的变化。随着加载的进行,η=0.00试样各个方向接触数量均增加,但水平倾向接触数量增加的更快,试样接触方向各向异性程度减小。η=1.25试样总接触数量有明显增加,但水平倾向接触数量基本不变,试样接触方向各向异性程度增加。
图8给出了非饱和重塑黄土离散元试样接触力偏组构随平均应力的变化。施加毛细力后,试样初始接触力偏组构(0.239)远大于初始接触方向偏组构(0.074),说明接触力的初始各向异性程度大于接触方向。η≤1.25试样的总接触力、强接触力(大于平均接触力)和弱接触力(小于平均接触力)偏组构均表现为随平均应力的增加先下降再增加;η≥1.50试样接触力偏组构(总、强、弱)随平均应力增加较快,最终达到较大的各向异性程度;侧限压缩试验接触力偏组构(总、强、弱)经历了“缓慢下降-快速下降-缓慢变化”的过程。在整个等应力比加载试验(不含等向压缩试样)过程中,接触力偏组构始终大于接触方向偏组构;强接触力偏组构大于弱接触力偏组构,即强接触力各向异性程度很高,对承担竖向荷载贡献大。

图6 接触方向组构特性
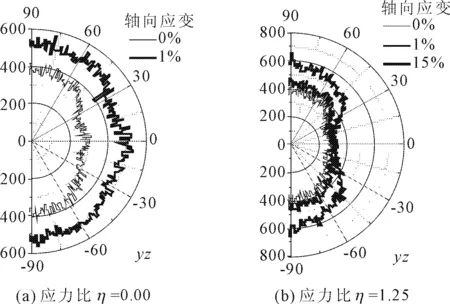
图7 接触方向组构玫瑰图
图9给出了接触力组构玫瑰图,在加载开始时接触力具有明显的各向异性;随着加载的进行,η=0.00试样水平倾向接触力数量明显增加,竖直倾向接触力数量略微减小,各向异性程度明显降低;η=1.25试样水平倾向接触力数量基本不变,竖直倾向接触力数量有一定的增加,各向异性程度增加。
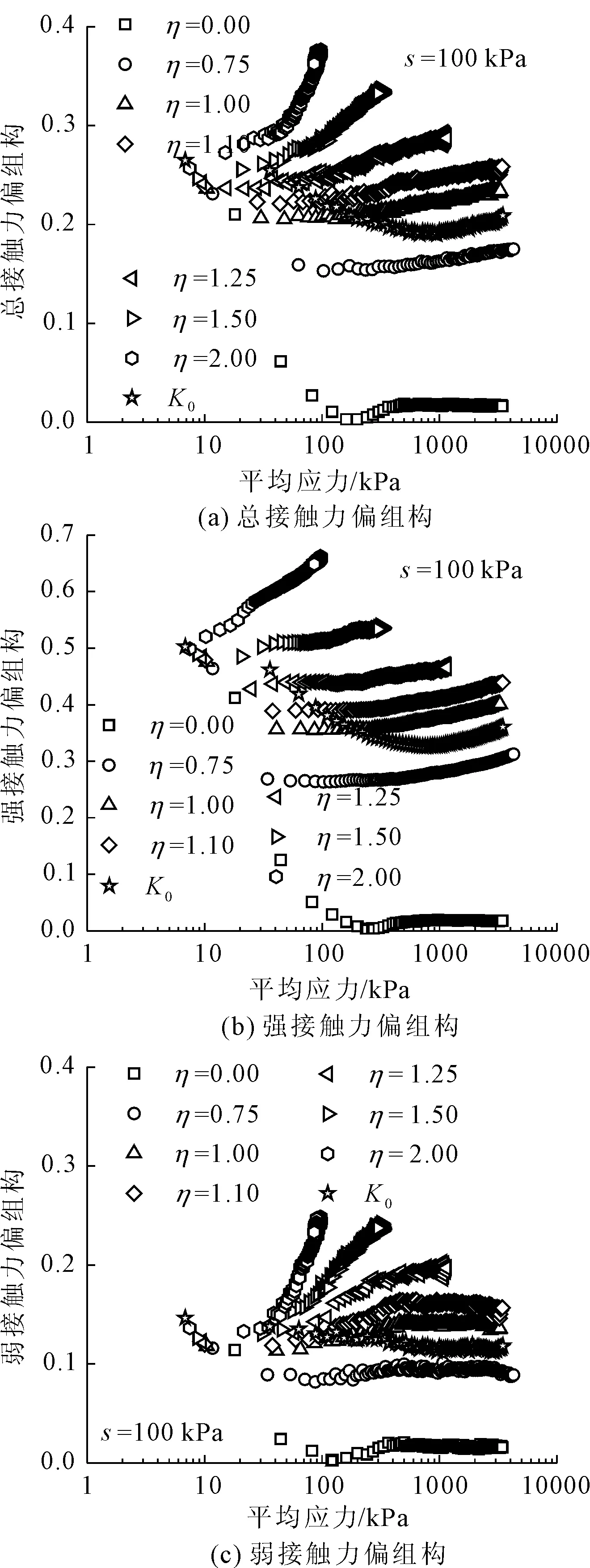
图8 接触力组构特性

图9 接触力组构玫瑰图
离散元试样反映了实际黄土的范德华力、毛细力、颗粒间摩擦和转动抗力等特征,但对颗粒级配、颗粒形状进行了简化,忽略了颗粒破碎。因此,离散元模拟仅能定性分析非饱和重塑黄土配位数和组构的变化规律,配位数和偏组构数值会与实际黄土有一定的不同,模拟的定性结果与微观观测结果[20]是协调一致的。
5 结 论
(1) 离散元模拟结果能定性再现室内等应力比试验的压缩曲线和剪切特性。在低应力比下(η
(2) 不同应力比试样的力学配位数在半对数坐标系中随平均应力的增加先缓慢增加后快速增加,不同应力比曲线具有很好的归一性;高应力比试样比低应力比试样有更多的颗粒参与了传力;临界状态对应的宏微观变量都基本保持不变。
(3) 试样接触方向偏组构的变化与其初始状态和加载应力比关系密切;侧限压缩的接触方向偏组构基本保持不变。在加载过程中(等向压缩试样除外),接触力偏组构始终大于接触方向偏组构;强接触力偏组构大于弱接触力偏组构。
