考虑卸荷带和岩体软化特性的某桥址边坡稳定性研究
2021-05-13杜杰贵李继兴夏艺峰
杜杰贵,严 松,李继兴,夏艺峰
(1.昭通市宜昭高速公路项目指挥部, 云南 昭通 657000;2.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室, 湖北 武汉 430071;3.中国科学院大学, 北京 100049; 4.昭通市宜昭高速公路投资开发有限公司, 云南 昭通 657000)
我国是地质灾害高发的国家,尤其是西南地区滑坡泥石流等地质灾害频发,严重影响西南地区经济发展,威胁人民生命财产安全,所以对工程边坡稳定性进行计算和评价具有重要的工程应用价值。
桥址边坡的选取要充分考虑其稳定性是否符合规定要求,是否会对修建、运营和后期养护产生影响,尤其是我国西南地区高山峡谷中的道路桥梁建设,因为在这些桥址所在位置,地形险峻、工程地质条件较为复杂、坡度大、岸坡高,桥址边坡本身的稳定性是桥位选择和桥基设计的重要影响因素[1]。
黄润秋等[2]对峡谷高陡边坡岩体卸荷机理进行了深入研究,分析了在边坡开挖或者河谷下切情况下的坡体应力分布特征,并提出边坡二次应力场理论,明确了两种卸荷裂隙的发育位置及其对坡体稳定性的影响。黄润秋[3]通过对西南地区强卸荷高边坡的研究分析,提出了河谷应力场“驼峰分布”模式,对由河谷高边坡应力释放所带来的浅表层破裂体系的形成机理与基本规律进行了详细地阐述。徐卫亚等[4]在野外工程地质调查和岩石力学室内外试验的基础上,采用数值模拟的方法,对某坝区边坡卸荷带岩体的工程地质特性和岩石力学参数进行了深入研究,建立了卸荷带的概化地质结构模型。蓝康文[5]对川藏铁路高山峡谷区进行了详细的野外调查,总结并分析了研究区边坡卸荷带的发育特征与分布规律并建立了边坡卸荷带变形破坏模式。
针对边坡软岩的工程特性,国内外学者进行了诸多研究[6-7]。常用的极限平衡法包括Bishop法、Morgenstern-Price法、Janbu法、Sarma法[8]以及通用条分法[9]等。随着对极限平衡法的深入研究,出现了无条分极限平衡法[10]和严格三维极限平衡法[11]。数值计算领域的飞速发展,对于边坡稳定性计算的方法也在不断完善,近年来,有限元、边界元、非连续变形分析(DDA)[12]等岩土工程数值计算方法逐渐普及,并在工程实际问题中广泛应用,尤其是有限元方法。部分学者通过建立地质力学模型对边坡软岩的力学特性进行了深入研究,肖克强等[13]通过建立地质力学模型试验,分析了软岩高边坡在开挖和降雨时坡体稳定性及变形的变化规律。杨晴霞[14]采用有限元软件建立软岩边坡地质模型,探究了降雨条件下边坡中孔隙水压力及暂态饱和区内岩体物理力学参数变化的共同作用下,边坡的破坏模式在时间和空间上的演化规律。
前人的研究大多考虑岩体卸荷带或软岩分布区单一条件下对边坡稳定性进行探究。本文主要分析含岩体卸荷带及软弱夹层的桥址边坡的稳定性。
1 桥址边坡概况
1.1 桥址边坡工程地质条件
桥址边坡工程地质条件较为复杂,区域内河谷两岸地形基本对称,呈“V”型。左岸边坡为顺向坡,总体坡度20°~30°,坡体中部斜向的发育一系列连续的30 m~60 m高的陡坎,陡坎的坡度可达45°以上,同时发育有与河道近于平行和正交的两组陡倾角节理。左岸工程区出露地层主要为二叠系上统玄武岩组上段,岩性有玄武岩、火山角砾熔岩和凝灰岩,由于受后期构造错动影响,岩体破碎,凝灰岩层间分布有不同规模的泥化夹层。右岸2 000 m高程以下,边坡坡度整体较稳定,一般在35°~43°,且在该段边坡连续发育多层高50 m~80 m的陡崖;2 000 m高程以上边坡坡度渐缓,坡度一般在10°~20°之间。桥址区域左岸岩体的卸荷深度最大到达90 m,对边坡稳定性产生较大影响的是凝灰岩泥化夹层和顺层特性,桥址左岸整体稳定性相较于右岸差,所以在桥基工程建设前期对左岸坡体稳定性进行系统评价是十分必要的(见图1)。

图1 桥址区左岸地形的地貌
1.2 计算坡面选取以及工况条件
桥址工程区边坡主要有五个比较桥位所在剖面的边坡,分别是Z1、Z2、Z3、Z4、Z5边坡,如图2所示,考虑桥址区实际工程地质情况选择了有代表性的Z3剖面进行极限平衡法稳定性分析。
根据桥址左岸的工程地质情况建立Z3剖面的地质概化模型,如图3所示,图中C点为主塔所在位置,B点靠近前缘卸荷带,这两点也是坡体潜在滑面剪入口。
参考《建筑边坡工程技术规范》[15](GB 50330—2013)与《公路路基设计规范》[16](JTG D30—2004),桥墩与锚墩所在位置边坡防治等级应拟定为一级边坡。《建筑边坡工程技术规范》(GB 50330—2013)规定一级永久边坡安全系数在一般工况下不小于1.350,地震工况下不小于 1.150。

图2 Z1—Z5剖面的空间关系
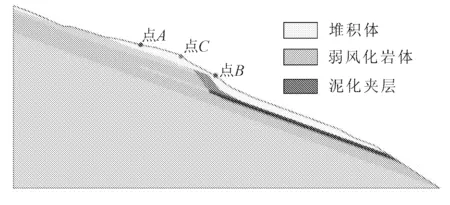
图3 Z3剖面左岸边坡计算模型
桥址边坡稳定性评价考虑4种不同工况分别为:(1) 自然工况,仅考虑岸坡受重力荷载作用;(2) 地震工况,桥址岸坡受地震荷载和重力荷载共同作用;(3) 桥基荷载工况,岸坡受到桥基荷载和重力荷载共同作用;(4) 地震工况和桥基荷载工况,岸坡受到重力荷载、地震荷载以及桥基荷载共同作用。根据桥址区域地震评价结果以及《公路工程抗震设计规范》[17](JTJ 004—89)要求,地震荷载采用拟静力法计算地震惯性力,计算中只计入水平地震力作用,水平地震加速度取0.2g。
2 桥址边坡稳定性分析
2.1 岩土体强度参数确定
凝灰岩是由火山喷发产生的火山灰沉积形成的,它的分布受多种条件因素影响,如火山喷发的规模、频率以及气候条件等,空间上分布通常很不均匀。凝灰岩由于粒度细、颗粒表面积大、孔隙率大,很容易发生次生变化,导致其强度和结构发生变化[18]。现场钻孔、平硐、坑槽勘探结果显示,桥址区域内凝灰岩空间分布极为不均,表现在层间错动的连续性及泥化夹层厚度上存在较大差别(见图4)。

图4 凝灰岩带岩体构成示意图
凝灰岩及其泥化夹层在坡体内分布不均,对边坡工程稳定性影响较大,为了进一步确定Z3剖面的主控地层的强度参数,现场平硐勘查结果揭示凝灰岩夹层分布比例为20%~60%,考虑凝灰岩分布比例对其的分布状况做三种情况考虑,分别为凝灰岩及其泥化带分布达到上限、下限和均值三种情况,全面考虑凝灰岩及其泥化夹层不同分布比例下的边坡稳定性状况。为了获取较为准确的计算参数,根据现场和室内试验的有关结果(见表1),在凝灰岩带上,由凝灰岩强度与玄武岩强度加权平均得到岩体等效或综合强度值,其加权平均表示式为:
(1)
(2)
其中:l1和l2分别为凝灰岩与玄武岩的长度;c1和c2分别为凝灰岩与玄武岩的粘结力;tgφ1和tgφ2分别为凝灰岩与玄武岩的摩擦系数。

表1 边坡岩体物理力学参数
通过凝灰岩带中凝灰岩和玄武岩占有的不同比例,得到各个剖面凝灰岩带岩体的综合抗剪强度参数,对处于卸荷带内的凝灰岩参数,通过对凝灰岩泥化带和玄武岩卸荷带进行不同比例的加权计算,结合该地区自然边坡的稳定性状态,采用极限平衡法对其参数进行正反分析和验证,获得了符合该边坡稳定状态的强度参数,具体见表2。
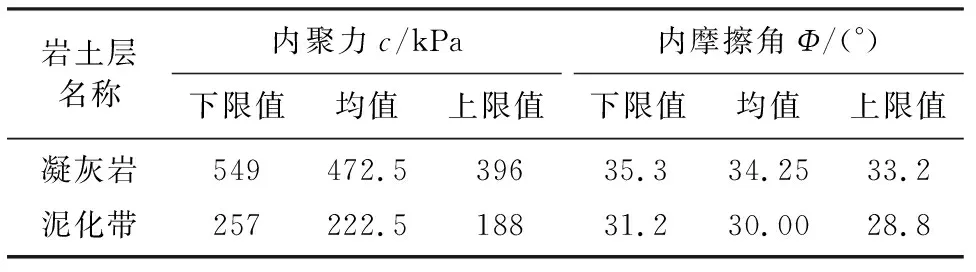
表2 凝灰岩及其泥化带抗剪强度参数
桥址边坡卸荷带岩体强度参数,基于坡体卸荷作用随埋深增大而减弱这一特点[19],结合现场平硐勘查结果以及现场剪切试验结果,边坡岩土体物理力学参数主要考虑三个分带:卸荷带内距坡面10 m以内,岩体强烈卸荷,结构面贯通性好,力学特性较差;距坡面10 m~20 m这一条带卸荷作用较弱,结构面贯通性较差,力学特性稍好;距坡面20 m之外为未卸荷带,结构面贯通性差,力学特性好。结合现场测试结果并反复试算,确定卸荷带岩土层的物理力学参数,具体见表3。

表3 卸荷带岩土层物理力学参数
2.2 桥址边坡破坏模式分析
黄润秋等多名学者基于工程实例、室内模型试验以及数值模拟等多种分析方法,研究发现边坡的变形破坏主要受控于层间软弱带及陡倾坡外卸荷裂隙,坡体中上部沿层间软弱夹层蠕变形成拉应力和剪应力集中,造成坡体前缘软弱带产生压缩变形并引起上覆岩体向坡外蠕滑并通过层面及卸荷裂隙面向上传递变形,最终其破坏模式主要表现为陡倾结构面与层间软弱带共同控制的阶梯状蠕滑-拉裂变形[20-23]。
结合前人研究成果,经现场勘查试验分析桥址区域稳定性控制因素主要为后缘卸荷带陡倾结构面和凝灰岩及其泥化夹层(见图5)。其破坏模式表现为牵引式滑动;此外,考虑到桥基处荷载作用较大,综合分析判断桥址岸坡滑动面可能位于前缘泥化带和桥基附近。
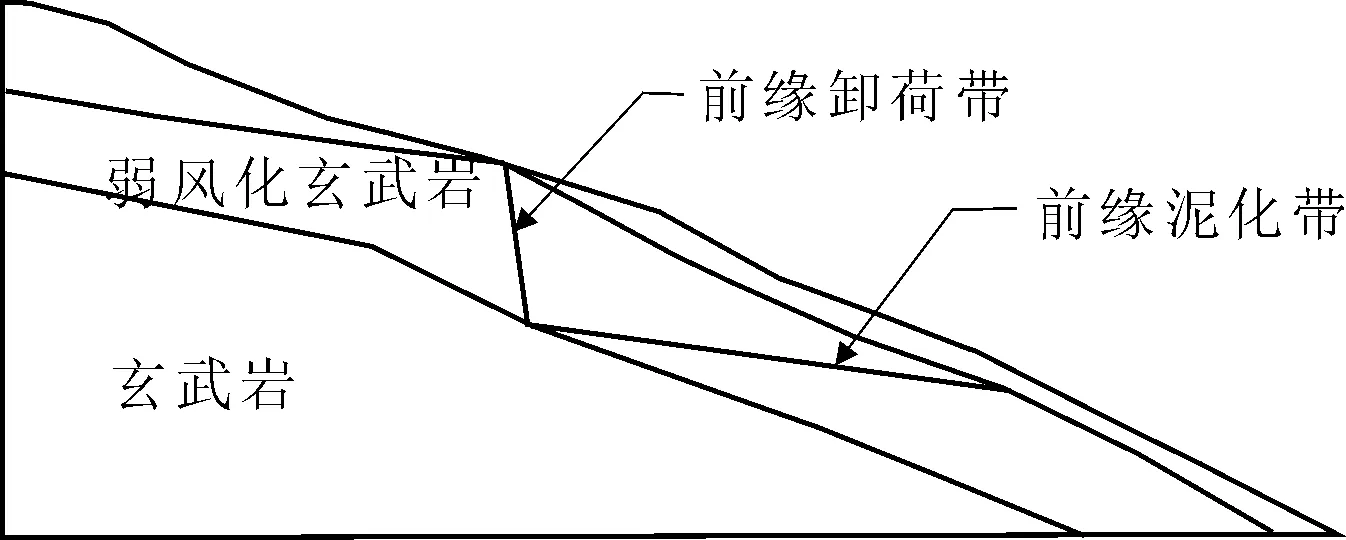
图5 边坡破坏模式示意图
2.3 桥址边坡稳定性计算分析
在保持平衡的颗粒介质中存在两种应力状态,一种是外部荷载的微小改变不会破坏原有的平衡状态,另一种是外部荷载的微小改变会导致原有平衡状态遭到破坏。第二种应力状态称为极限应力状态,其构成了极限平衡的理论基础[6]。
在土力学中,Mohr-Coulomb强度理论被广泛运用[24],其表达式为:
τf=c′+σ′tanφ′
(3)
式中:τf为土体抗剪强度;c′和φ′为抗剪强度参数;σ′为破坏面上的正应力。
在有限元极限平衡法中,对任意的滑动面l,安全系数Fs定义为:
(4)
式中:n为滑动面l离散的线段数;Δli是离散线段i的长度。
安全系数的计算在通常情况下,土的抗剪强度满足Mohr-Coulomb强度理论,安全系数可以表示为:
(5)
将滑动面l离散成n个微小的线单元i,安全系数为:
(6)
桥址边坡的稳定性性计算采用适合边坡失稳破坏模式的Janbu法为主要的计算方法,不同工况边坡稳定性计算结果如下。
自然工况下桥址边坡稳定性计算结果如图6所示。随着凝灰岩分布比例由20%增加至60%,坡体综合抗剪强度参数逐渐降低,其对应边坡滑移面的安全系数也相应下降。凝灰岩分布比例取下限时,最小安全系数为2.323;凝灰岩分布取均值是,最小安全系数为2.153;凝灰岩分布取上限时,最小安全系数为1.984;在这三种凝灰岩分布情况下,边坡安全系数最小的潜在滑移面均位于坡体前缘卸荷带附近,其次,桥基处的安全系数有所下降,但下降幅度较小,边坡整体上满足稳定性要求。
在地震工况下,随着凝灰岩分布比例变化,边坡安全系数变化如图7所示,当凝灰岩分布比例为下限、均值和上限时,边坡最小稳定性系数分别为1.928、1.784和1.640。通过与图6对比可以看出,地震工况下边坡安全系数随剪入口位置变化趋势与自然工况下的变化趋势基本相同,边坡安全系数最小的滑移面均位于坡体前缘卸荷带附近。
通过计算结果可以明显看出,在天然状态下,桥址边坡稳定性主要受控于坡体前缘凝灰岩泥化带,地震工况下最小安全系数相较于自然工况减少了17%。其次,凝灰岩夹层分布比例越高,贯通性越大,对坡体稳定性影响也较为明显,上下限值之间的安全系数变化幅度约为15%,但边坡稳定性仍满足设计建设要求。
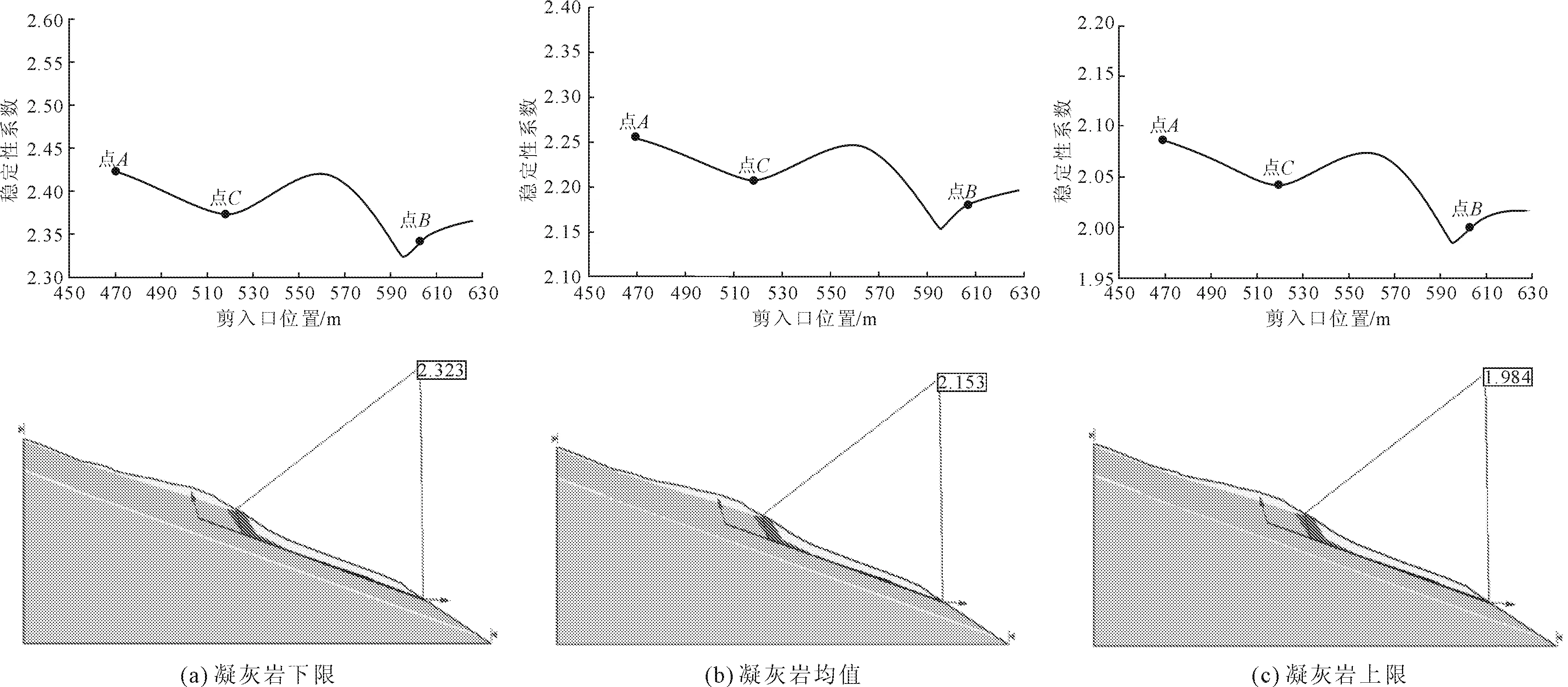
图6 自然工况下边坡安全系数随剪入口位置变化情况
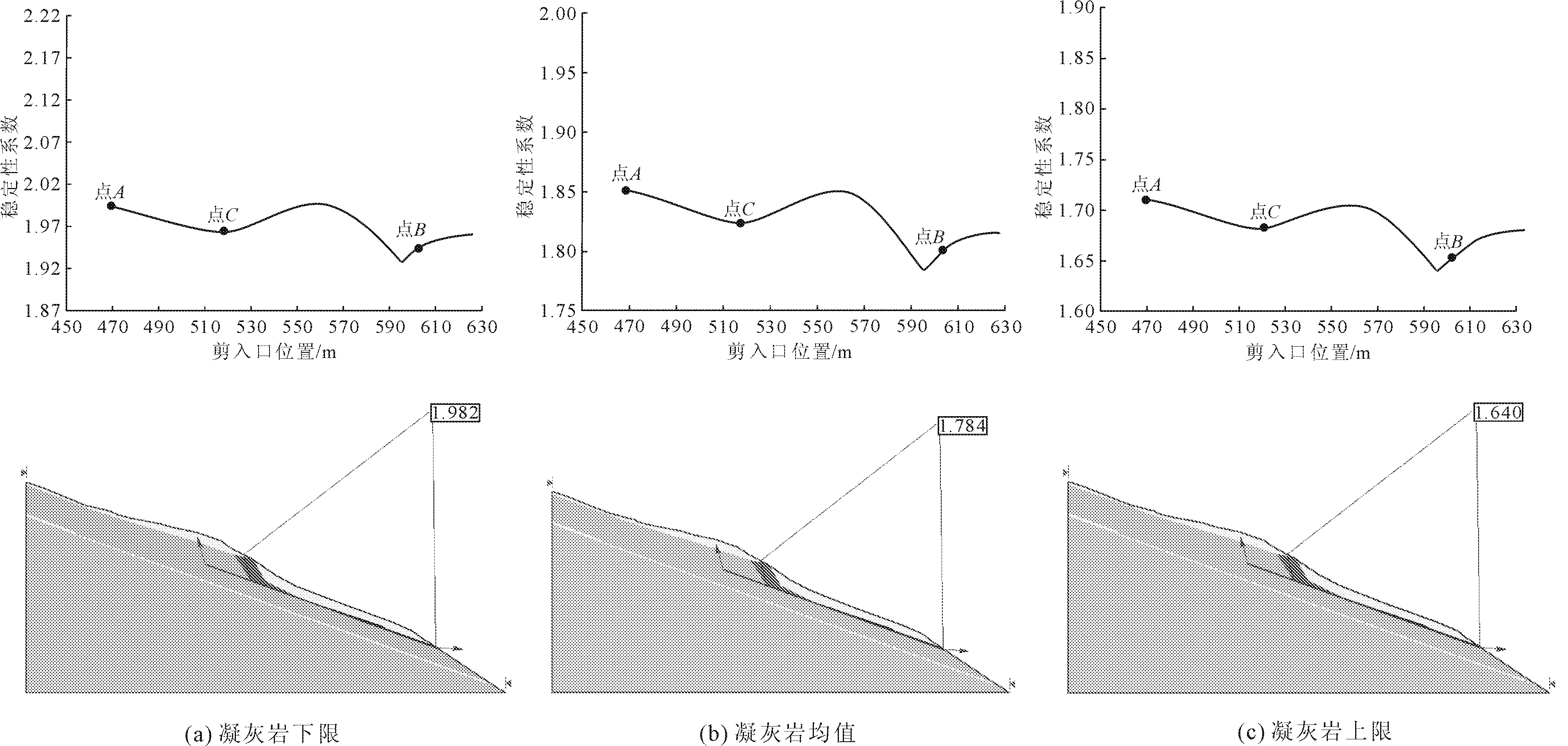
图7 地震工况下边坡安全系数随剪入口位置变化情况
在桥基荷载工况下,作为外部荷载将桥基荷载转化为节点力施加在计算模型上。图8给出了桥基荷载作用下,凝灰岩的分布情况对坡体稳定性系数的影响以及与自然工况下安全系数变化的对比。从图中可以看出,凝灰岩分布三种不同的情况下,边坡安全系数最小为1.803,最危险的滑移面位于桥基附近。计算结果显示出,桥基荷载作用下边坡稳定性满足规定要求。
考虑工程实际中最不利的情况,桥基荷载和地震荷载共同作用下,边坡稳定性安全系数的变化情况如图9所示。边坡最小安全系数为1.526,凝灰岩三种不同的分布情况下,最危险的滑面位置均位于桥基附近,但边坡整体仍满足稳定性要求。
通过图8和图9中自然工况与桥基荷载工况和桥基荷载与地震荷载共同作用下安全系数变化趋势对比可以看出,考虑桥基荷载作用的情况下,岸坡的最危险滑移面由坡体前缘卸荷带移至桥基附近,安全系数也降低了23%,尤其是桥基附近降幅最大,但坡体后缘和前缘稳定性系数变化较小,说明桥基荷载对该岸坡中后缘和前缘稳定性影响不大,对桥基附近的局部稳定性影响较大。
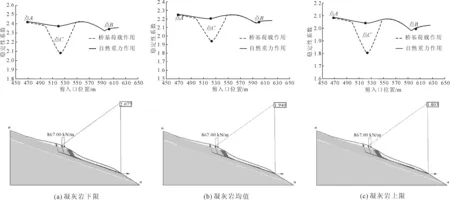
图8 桥基荷载工况下边坡安全系数随剪入口位置变化情况
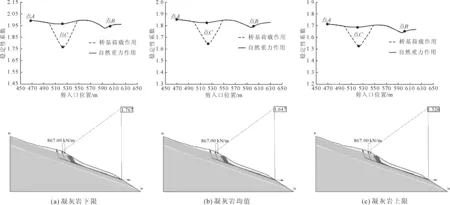
图9 桥基荷载和地震荷载作用下边坡安全系数随剪入口位置变化情况
3 结 论
文章通过现场测试试验以及正反分析计算获得了某桥址边坡的卸荷带及软化带岩体强度参数,采用极限平衡法分析了某桥址边坡的稳定性并进行了系统评价,得到结论如下:
(1) 针对凝灰岩及其泥化带分布不均,物理力学参数难以确定,采用岩体综合强度的计算方法,结合现场自然情况下坡体的稳定性状况,利用极限平衡法对岩体综合强度参数进行正反分析和验证,获得了符合该边坡稳定状态的材料参数,为复杂岩性条件下获取合理的岩体计算参数提供了参考。
(2) 受卸荷带结构面影响,自然工况和地震工况最危险的滑移面剪入口位于坡体前缘的卸荷带;桥基荷载作用下,潜在滑移面剪入位置由坡体前缘卸荷带移至中缘桥基位置处,说明桥基荷载是影响滑移面剪入位置的主要因素。
(3) 通过四种不同工况的计算结果对比可以看出,在自然工况和地震工况下,桥址边坡稳定性较好;桥基荷载对边坡的稳定性影响较大,相对于自然工况安全系数降幅达23%,但在最不利的工况下最小安全系数为1.526,依然满足工程设计建设要求。
