面向密集多波束组网的卫星通信系统资源调度算法

何元智，彭聪,2，于季弘，刘韵

（1.军事科学院系统工程研究院，北京 100141；2.空军工程大学信息与导航学院，陕西 西安 710077；3.北京理工大学通信与网络实验室，北京 100081）

1 引言

随着空间信息技术的快速发展，近年来国内外卫星互联网纷纷展开部署。国外代表性系统主要包括全球星系统、铱星系统、星链系统等[1-3]；我国把卫星互联网建设纳入“新基建”范畴，并且将其定位为国家战略性工程[4]，代表性系统包括鸿雁星座、行云工程、虹云工程、天象星座等[5-7]。作为未来空天地一体互联网络的重要组成部分，卫星通信系统具有广覆盖、低时延、大宽带、小终端等特点，正在朝着空天地密集多波束组网的方向发展。然而，空间轨位与频谱资源的竞争愈演愈烈，并伴随空间业务量的爆发式增长，导致卫星通信系统面临的压力巨大，因此需要在满足用户需求时，对有限的卫星资源进行合理调度，这对于实现星地之间高效协同、统筹组网具有十分重要的现实意义。

在密集多波束星地一体化组网条件下进行卫星资源调度会面临星地动态变化、多波束负载差异、星上资源受限等挑战，需要在一定的时间窗口内对有限的星上资源进行全局规划和多目标化。文献[8]对观测能力有限的多卫星资源调度问题进行了研究，并将其转化为组合优化问题，同时提出了一种二阶启发式方法，在合理的计算时间内获得高质量的解。文献[9]提出了一种基于分治原则的新型卫星调度框架，在此框架下，采用蚁群优化算法将观测任务分配到不同的卫星轨道，并设计了一种自适应模拟退火算法来解决每个轨道的卫星观测问题。文献[10]提出了一种分层调度方法来解决卫星实时调度问题，将调度过程分为3 个步骤，即预调、粗调度、精调度，在此基础上提出了一种基于蚁群优化的分层调度算法。文献[11]首先分析了卫星距离调度问题，并建立了数学模型和约束条件，然后提出了一种将改进遗传算法和局部搜索方法相结合的高效算法，利用改进的遗传算法快速提高规划方案的质量，并利用邻域搜索进行后续的小规模优化。文献[12]提出了一种基于深度神经网络的多卫星资源调度方法，通过将多个约束和相关属性转换为不同的标志，并使用数据的一些二进制位来反映约束关系，提高了资源的利用效率。文献[13]提出了一种结合软件定义网络（SDN,software defined network）模型的三层网络体系结构，用于指导卫星间链路（ISL,inter-satellite link）连接和卫星边缘计算的资源调度，并提出了先进的k 均值算法和基于广度优先搜索的生成树算法，分别实现了卫星边缘计算资源划分和ISL 构建。上述研究都从具体的约束出发，基于不同的应用场景建立资源调度模型，并提出优化算法求解资源调度问题，但是这些算法仅适用于特定网络场景，不能很好地适用于密集多波束卫星通信网络的资源调度，且算法复杂度较高。

资源调度的核心是资源调度算法，常用的有遗传算法、蚁群优化算法、粒子群算法以及它们的组合[11,14-18]，这些算法对于一般规模网络的资源调度能够达到很好的优化效果，但在密集多波束组网的条件下，算法的复杂度会急剧上升，因此需要在算法的优化性能和复杂度之间进行折中。对于卫星资源调度来说，还需要考虑实现的难易程度，蚁群优化（ACO,ant colony optimization）算法作为一种启发式寻优搜索算法，常用于求解路由最短路径以及多目标资源优化问题，具有控制简单、兼容性强、对硬件要求不高以及易于编程实现等特点，对于解决密集多波束、高动态的卫星资源调度问题具有一定优势。然而，初始阶段信息素匮乏导致的搜索速度过慢以及局部搜索能力较弱等特点严重制约该算法在实时性、高效性需求较强的卫星调度过程中的应用，需要对其进行改进。

基于上述考虑，本文分析了密集多波束组网场景下卫星通信系统资源调度的约束条件，建立了多目标资源调度模型，综合考虑了现有蚁群优化算法的优缺点，并针对存在的缺点，提出了以初始解集构造和额外信息素沉积为核心的改进蚁群优化算法，最后设计了仿真场景对模型和算法进行了仿真验证。

2 卫星通信系统资源调度问题建模

在卫星通信系统中，随着卫星在轨移动，其覆盖范围将发生变化，对应的业务负载以及优先级也会随之变化。为了满足不断变化的地面任务需求，需要对卫星资源、信道资源以及时隙资源进行合理调度，资源调度问题主要受到时间窗口约束、卫星功耗约束、信道数量约束、地面用户优先级以及突发性等条件影响，其目标是在满足这些约束条件的前提下，保证系统的功耗尽可能小，调度完成的高优先级的任务尽可能多。

2.1 系统模型

卫星通信系统的资源调度场景如图1 所示。卫星通信系统由M颗多波束通信卫星组成，对地面用户进行动态覆盖，不同卫星波束的覆盖区域之间存在一定的重叠。将系统所能覆盖的区域范围划分为N个地面区域，通信任务根据其发起用户所在位置分别归属于不同的地面区域。

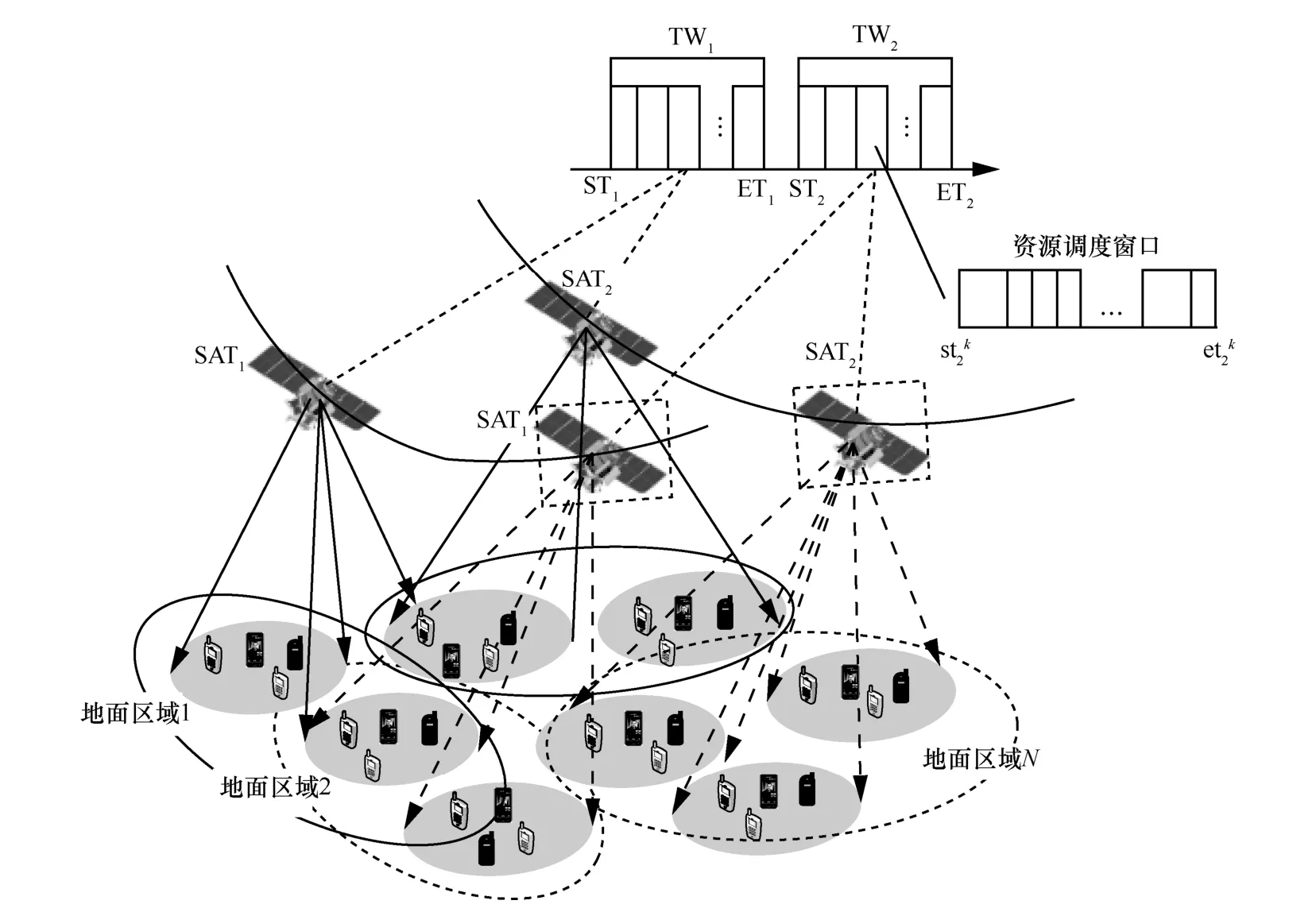
图1 卫星通信系统的资源调度场景示意

考虑到随着卫星的在轨移动，即图1 中SAT1和SAT2由左侧位置沿轨道移动至右侧位置时，各波束所覆盖的地面区域随之发生变化，设置时间窗口为TWi,i=1,2，以时间窗口长度为粒度对卫星通信资源进行优化，其中，T W1表示当前时间窗口，TW2表示下一个时间窗口，时间窗口的起止时间为[S Ti,ETi]。时间窗口可划分为Nk个资源调度窗口，为任务的最大分配单元，当任务的起止时刻包含于资源调度窗口内时，才能有效地执行任务的传输。每个资源调度窗口持续K个时隙，第k个资源调度窗口的开始时刻和结束时刻分别为和。

在时间窗口TWi中，来自第n个地面区域的通信任务可以表示为一个五元数组，即

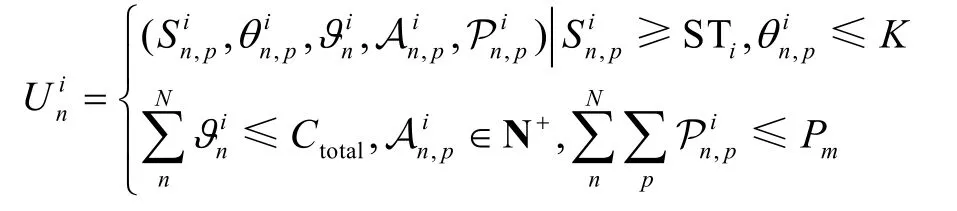
2.2 资源调度模型

基于以上对系统模型的分析，以地面任务服务质量以及卫星通信系统的总功耗为目标，本文建立了如式(1)所示的卫星通信资源调度模型。

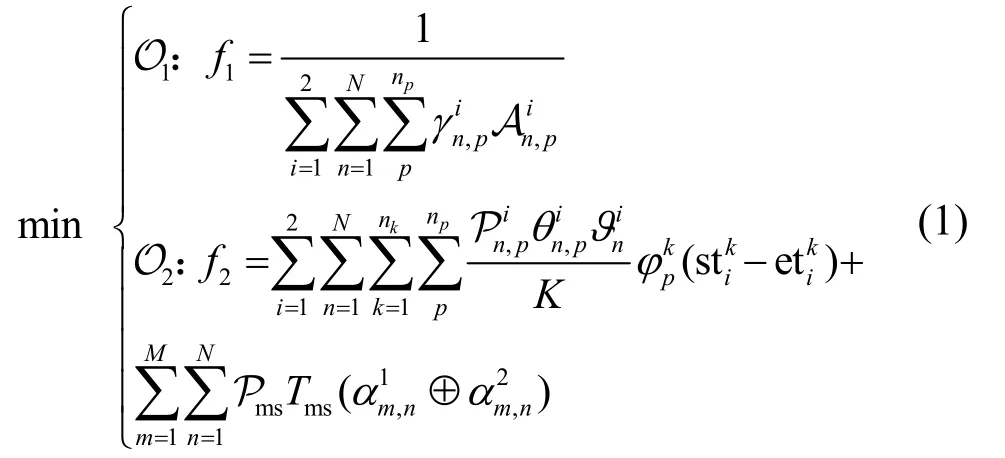
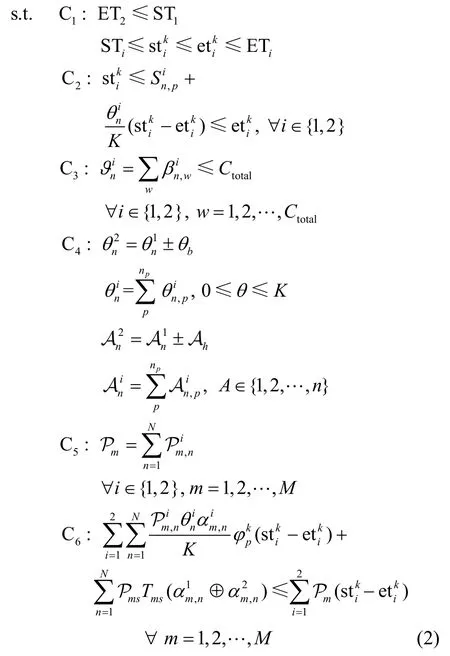
上述模型中，目标函数 O1表示在2 个时间窗口内卫星通信系统尽可能完成多个高优先级任务的传输，即调度完成的高优先级业务总和的倒数最小；目标函数 O2代表2 个时间窗口内系统总功耗最小，总功耗主要由2 个部分组成，第一部分为任务传输功耗，第二部分为切换功耗。其中，Pms为单位时间切换的功率大小，Tms为连续执行资源调度需要最大切换时间，只有当=1时，不需要进行卫星切换，即。

在约束条件中，C1为时间窗口起始时刻约束，目的是确保2 个时间窗口不发生重叠，且各资源调度窗口均完整地位于时间窗口内部。C2表示任务有效执行时间约束，即只有当任务的起止时刻包含于时间调度窗口内时，才能有效地执行任务的传输。C3为信道数量约束，即为每个区域分配的信道数量总和应该小于总的信道数量。C4为任务状态更新方程，考虑到任务随时间的连续变化性，下一个时间窗口有可能出现优先级较高的“热点”任务或突发性较强的重负载任务，即任务突发情况，或者出现大量低优先级、轻负载的任务，即任务减少情况，这时需要对网络资源的调度进行调整。通过定义时隙数调整量θb，描述地面区域在前后2 个时间窗口中占用时隙数的弹性变化，通过定义优先级调整量Ah，描述地面区域在前后2 个时间窗口中的优先级变化。C5为卫星与地面任务的功耗关系，对于每一颗卫星而言，它所提供的功率等于其覆盖区域内所有任务功率的总和，且必须小于卫星所能提供的最大功率。C6为功耗约束，即覆盖区域内所有任务的传输功耗与卫星的切换功耗之和不超过卫星在这2 个时间窗口内所能提供的功耗总和。约束条件C1和C2是确保资源调度成功的时间窗口约束，即保证任务的起止时间要落在资源调度窗口内；C3、C5和C6分别是信道约束、功率约束和功耗约束，对应卫星的通信资源；C4是时隙调整和优先级调整，用于刻画地面通信任务的连续动态变化特性。

在整个资源调度过程中，进行如下假设。

1) 2 个时间窗口的任务传输与资源调度相互独立，任务传输具有连续性，并且只在时间窗口内进行，如果任务传输的终止时间超过了时间窗口的终止时间，则判定任务传输失败。

2) 第一个时间窗口结束后，需要对任务集合进行更新，下一个时间窗口不同区域的突发性大小主要影响任务传输所需要的时隙数，“热点”性强弱主要影响任务的优先级。

3) 信道分配取决于任务需求，前提是不能超过信道总数，在进行任务传输的时候，忽略信道损耗对功耗的影响。

2.3 资源调度问题分析

通过观察上述资源优化问题的数学模型，2 个优化目标函数虽然在求解参数上并不强相关，但由于优先级加权和与功耗同处于N个地面区域和M个卫星提供服务的约束之下，使约束条件空间的参数下标之间存在相关性，导致使数学模型中2 个优化目标之间具有强耦合特性，因此，2 个优化目标不能拆解为单独的优化目标函数求解。

实际上，上述问题的关键在于目标函数 O1中的优先级权重，若只考虑目标函数 O2，其最小值的解集空间为考虑优先级权重，在业务量大于系统可调度资源时，可能导致为了节约功耗放弃部分高优先级业务调度的问题，即最低功耗解不一定是最高优先级加权和任务完成度的解。因此，上述优化函数的数学含义是寻找优先级加权和任务完成度和功耗之间的折中。但由于2 个优化问题的参数空间的强耦合特性，无法通过简单的参数代入推导获得解析解，也无法通过参数空间合并转化为单目标优化问题再通过凸优化方法求解。针对这类问题，数学上通常通过遍历搜索的方法来求解。

然而，遍历搜索的方式由于要穷举解集空间，其算法复杂度与解集空间的大小强相关。首先，分析目标函数 O1，其中，任务传输完成标识具备2个状态0 和1，即对于x个该类标识的组合，组合可能为2x个，那么，O1解空间大小为

通过上述分析，解空间大小为指数函数，意味着遍历求解方式的计算复杂度随着参数下标的大小呈指数增长。实际上，优化问题根据其是否可以在多项式时间内求解，通常可以分类为多项式（P,polynomial）问题和非多项式（NP,non-deterministic polynomial）问题，上述问题的计算复杂度为非多项式函数，是典型的NP 问题。为了求解该问题，需要通过多轮次迭代寻找求解搜索方向，以避免无方向的遍历带来的指数级复杂度。蚁群优化算法作为一种模拟进化算法，是一种用来在图中寻找优化路径的随机算法，可用于本文的优化问题求解。

3 卫星通信资源调度算法设计

基于对蚁群优化算法优缺点的综合考虑，本文以提高算法初期搜索速度和局部搜索能力目标，提出一种改进的蚁群优化算法来解决多约束条件下的卫星通信系统资源调度问题，算法流程如图2所示。

3.1 初始解集构造以及信息素的更新

在蚁群优化算法中，对于每一个解元素Γi=(α,β,γ)来说，都有一个信息素浓度τi与之对应。信息素浓度的更新为

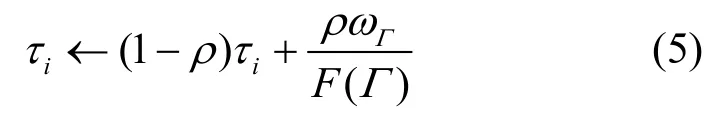
其中，ρ为挥发速率，ωΓ为解元素Γi的权重因子。首先，通过蒙特卡罗仿真产生初始解集空间，然后将解集与任务集合进行映射。为了提高算法初期的搜索速度，本文定义了质量函数F(Γ)=f1，其目标是确保调度完成的任务的优先级尽可能高。任务按照优先级的大小依次传输，如果任务的传输时间不能满足时间窗口约束，则视为无法传输，可以把这些任务所对应的解元素从解集空间中删掉，最后确定初始的解集范围。

我州每年会有大量农村初中毕业生直接进入劳动力市场，既降低了劳动者素质，又影响了经济发展质量。据调查，我州近几年专业技能人才缺口上万人，而职业教育输送的人才数量远不能满足经济社会发展需要。因此，高素质技能型人才短缺依然是产业发展的瓶颈。

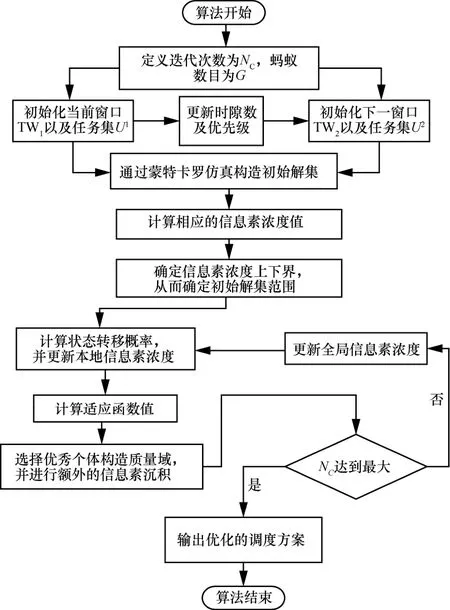
图2 卫星通信系统资源调度算法流程

3.2 状态转移概率的确定

对于时间窗口TWi，假设τm,n,w为第m颗卫星通过信道w完成对区域n中的调度任务的信息素浓度，则转移概率式为

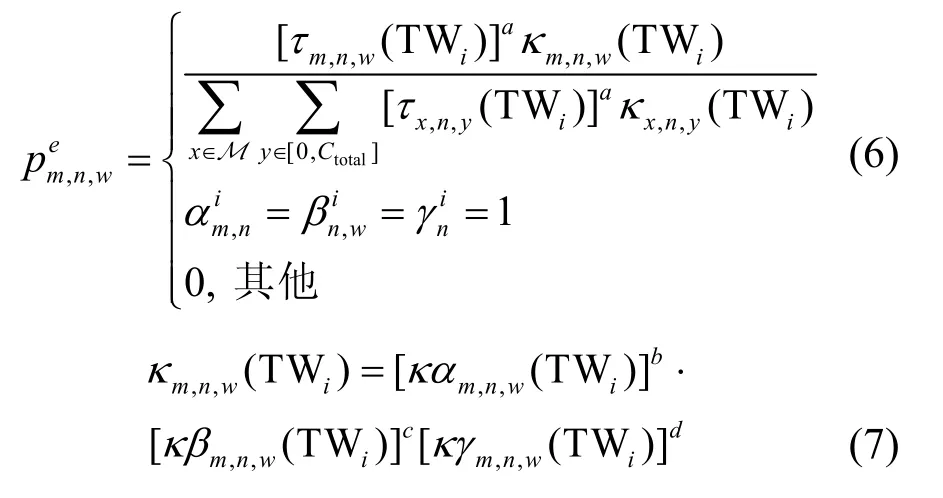
其中，a为信息素启发值权重，用来描述信息素浓度对于调度任务的影响程度，其值越大，蚂蚁对走过的路径选择的概率越大；κm,n,w(TWi)为第m颗卫星通过信道w完成对区域n中的调度任务的启发程度；καm,n,w(TWi)为卫星调度的启发值；b为相应的启发值权重；κβm,n,w(TWi)为信道分配的启发值；c为对应的启发值权重；κγm,n,w(TWi)为任务调度的启发值；d为对应的启发值权重。b、c、d值的选取决定了算法的局部搜索能力。

3.3 信息素上下界的确定

在实际的优化场景中，为了在有限次数的迭代之后找到最优解，需要确定信息素值的上下界。在每次迭代的过程中，解集的更新必定会导致信息素值的更新，假设τ0为初始的信息素值，LF和UF分别为质量函数的下界和上界，在N次迭代后可以计算出τi的上界为Uτ。

式(8)右侧的第一项为挥发速率对信息素浓度的影响。式(9)为归一化权重，其中，ηv和ηu表示与挥发速率成比例的权重值。同理，本文可以得到信息素下边界为Lτ。当迭代次数较大时，(1 −ρ)N(τ0−ηUF)→0，因此信息素上下界可以表示为ηu LF≤(τi)N≤ηUF。

3.4 适应函数确定

对于资源调度的多目标函数，采用线性加权的方式作为其适应函数，如式(12)所示。

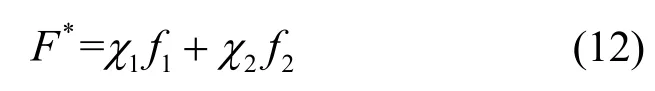
其中，χ1+χ2=1。在计算适应度值之前将优先级目标函数和功耗目标函数进行归一化，根据2 个目标函数的重要程度来确定相应的权值大小，在偏好关系上，f1的重要程度远比f2重要，因此对应的权值关系为χ1≻χ2。

3.5 额外信息素沉积

为了进一步提高收敛速度，本文在每次迭代中将更新扩展到有限元素，以便更多的解元素能够更新它们的信息素值。本文提出了自适应信息素更新方法，在所有选中的解集方案中，选择部分解元素进行额外的信息素沉积，主要思想是构建一个质量域BQ，如式(13)所示。

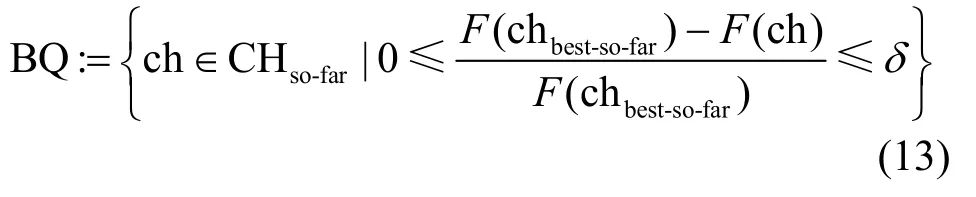
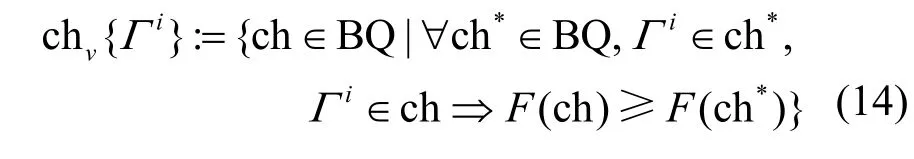
如果在质量域中存在多于一个优化解，则选取一个质量值最大的作为chv{Γi}。最终，可以进行一次额外的信息素值更新，如式(15)所示。

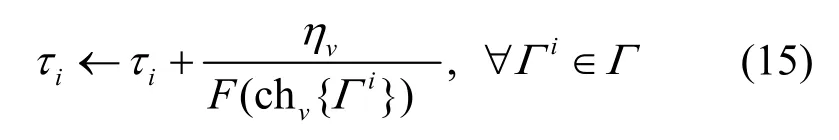
3.6 算法复杂度分析

对于蚂蚁种群规模为G，迭代次数为Φ的资源调度问题，每个蚂蚁个体是由二进制变量集合所决定的。假设第N个区域的任务总数为YN，第i个时间窗口的任务调度窗口的个数为Xi，则算法的复杂度

由此可知，算法的时间复杂度与蚁群规模、迭代次数、地面任务负载轻重以及总的信道数目有关。在密集多波束组网时，地面任务负载较重，并且信道数目以及时间窗口不变，为了降低算法的时间复杂度，本文通过初始解集的构造以及额外信息素的沉积加快了算法收敛速度，减少了迭代次数，因此大大降低了时间复杂度。

4 仿真以及结果分析

4.1 仿真过程实现

仿真分析基于5 颗卫星（SAT1～SAT5）和7 个地面区域（Z1～Z7），卫星的轨道高度和倾角如表1所示，仿真的时间段为00:00:00—06:00:00，地面任务区域彼此不重叠地分布于300 km×200 km的方格内，利用STK 软件对地面任务区域进行可见性分析，可以获得地面区域的任务调度窗口。资源调度过程仿真实现基于MATLAB R2019，在2 个时间窗口内，卫星对地面区域的覆盖情况如图3 所示，单个地面区域可能同时被多个卫星所覆盖，因此需要综合考虑任务需求和卫星现有的资源状况来选择合适的卫星进行资源调度，各个地面任务区域对应的可视卫星以及相应优先级的任务数如表2 所示，其中，Am(n)代表第m种优先级对应的任务数量为n。

表1 卫星轨道参数

在仿真场景中，综合考虑全球星、铱星、星链等实际在轨卫星的单星参数及其平台类型和未来密集多波束组网场景的用户服务需求，假设5 颗卫星的可用信道总数Ctotal为100，单个信道的功耗为20 W，每个卫星所能提供的功耗Pm为400 W。在改进的蚁群优化算法中，蚂蚁的数量为30，根据ACO算法参数设置[19]，信息速率的挥发速率ρ为0.03，适应函数的权值χ1和χ2分别为0.64 和0.36，状态转移概率启发权重a、b、c、d分别为2、4、2.5、0.5，额外信息素沉积的质量域半径δ为0.2。

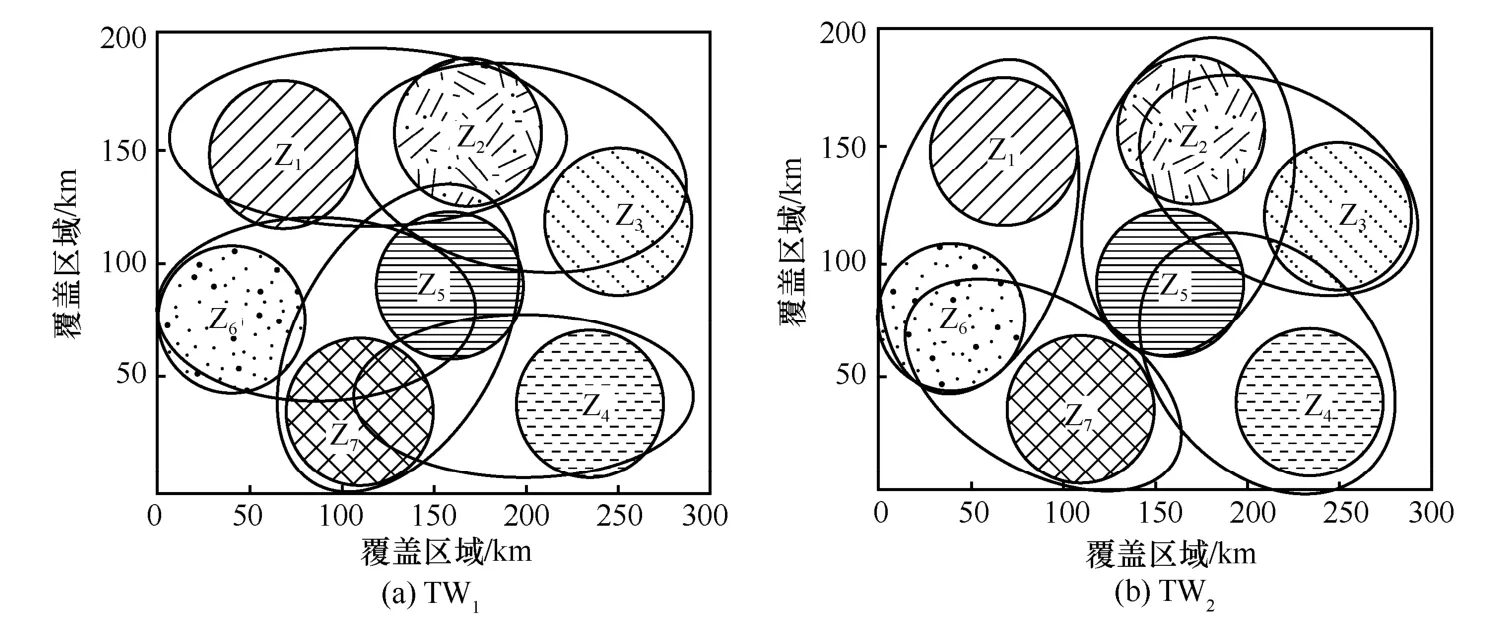
图3 卫星对地面区域覆盖情况

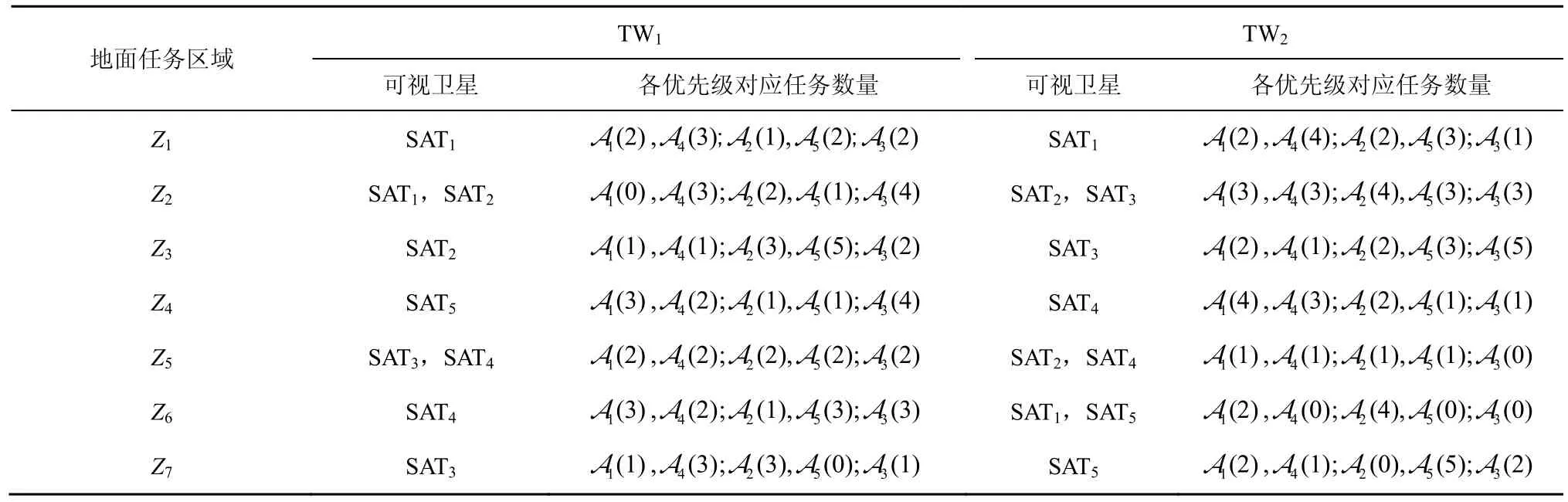
表2 各个地面任务区域对应的可视卫星以及相应优先级的任务数

为了分析所提算法的性能，本文首先选取调度完成的任务数以及调度完成的任务总优先级作为评价指标，将所提算法与传统蚁群优化算法进行比较来分析算法的敛散性能，然后与智能蜂群算法[20]进行对比，分析了所提算法在资源调度效率和功耗方面的优化性能。智能蜂群算法作为一种群智能优化算法，将求解优化问题的过程转化为蜂群寻找优良蜜源的过程，通过智能调整转移因子与状态转移变量来进行优化求解，能够克服早熟现象，收敛速度快，相比于传统蚁群优化算法具有一定优势。

4.2 仿真结果分析

图4(a)和图4(b)分别给出了剩余任务数量和调度完成任务优先级随时间的变化，2 个时间窗口都为32 s，为了反映地面区域任务负载的变化情况，将2 个时间窗口的任务以及相应的优先级放在同一个坐标系内进行比较，如图4(a)所示，无论初始的任务负载有多重，剩余未完成的任务数量总能在20 s以后保持稳定，从侧面反映了在给定的约束条件下，算法的收敛时间大约为20 s。如图4(b)所示，无论任务负载轻重，开始调度完成任务总的优先级都相等，这是因为刚开始的时候系统资源充足，优先级最大成为唯一约束，随着时间的推移，系统资源消耗增加，此时需要与优先级进行综合考虑，寻求总的效益最大化。

1) 算法敛散性能分析

算法的敛散性是衡量蚁群优化算法的重要指标，通过解集构造以及额外信息素沉积将极大地提高算法的收敛速度，与传统的蚁群优化算法进行比较，所提算法能更快地收敛到目标值。如图5(a)和图5(b)所示，所提算法在经过63 次迭代后完成收敛，而传统的蚁群优化算法需要87 次迭代，并且所提算法经过迭代后剩余未调度完的任务数要少于传统蚁群优化算法，而调度完成任务总的优先级要高于传统蚁群优化算法，可以看出所提算法的优化性能也有一定程度的提高。

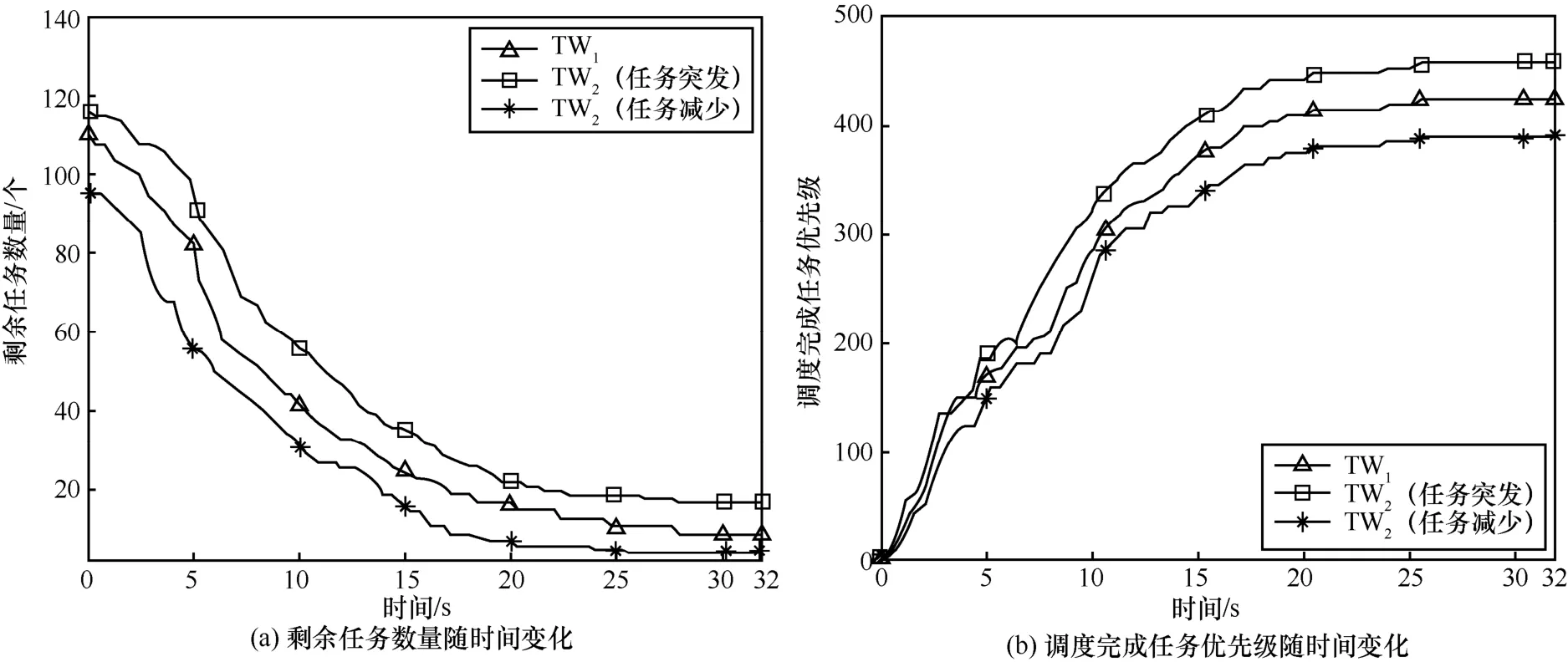
图4 剩余任务数量和调度完成任务优先级随时间变化

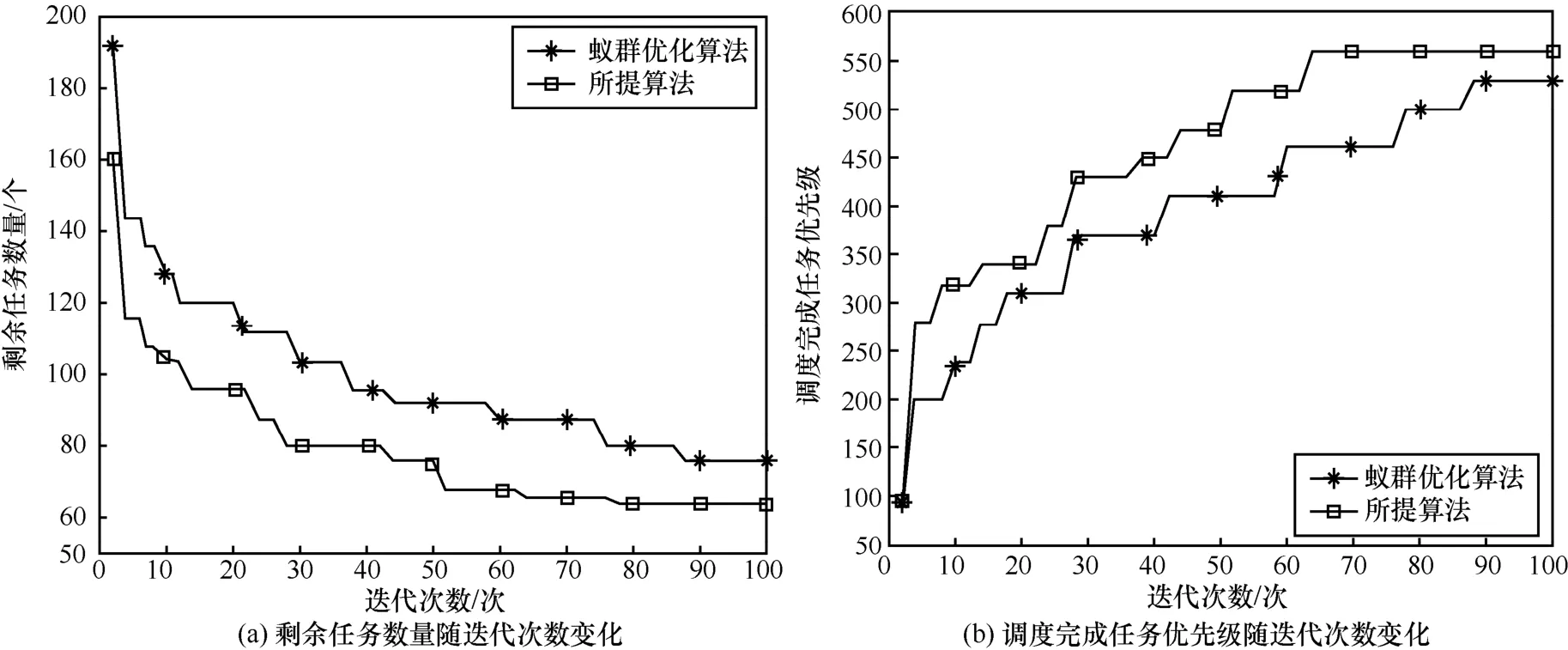
图5 剩余任务数量和调度完成任务优先级随迭代次数变化

2) 算法优化性能分析

图6 为3 种算法的未调度成功任务数量随总任务数量变化关系。从图6 中可以看出，随着总任务数量的增加，未调度成功的任务数量也增加，这是由于系统资源有限，当任务负载较重时，调度失败的概率会大大增加，在相同的总任务数量条件下，所提算法未调度成功的任务数量明显低于其他2 种算法。

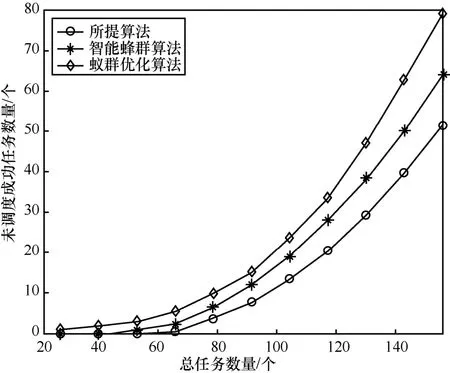
图6 未调度成功任务数量随总任务数量变化关系

图7 为3 种算法的功耗随总任务数量变化关系，在一定的功率约束下，系统总功耗随着任务数量增加而增加，其中，所提算法在功耗性能方面表现最优，分别减少了约29.13%和16.82%。

图7 总功耗随总任务数量变化关系

图8 为3 种算法的任务完成时间随总任务数量变化关系。从图8 中可以看出，在不同的任务规模下，所提算法完成任务调度所需要的时间最短，从侧面反映了所提算法的收敛速度最快。总体来说，无论是任务调度成功的数量、算法能耗还是任务完成时间，所提算法都优于其他2 种算法，这主要是由于所提算法进行了初始解集构造、基于质量域的精英选择机制以及额外信息素沉积，能够在迭代的过程中快速找出优秀个体，并且将其保留，使算法快速收敛到最优解。

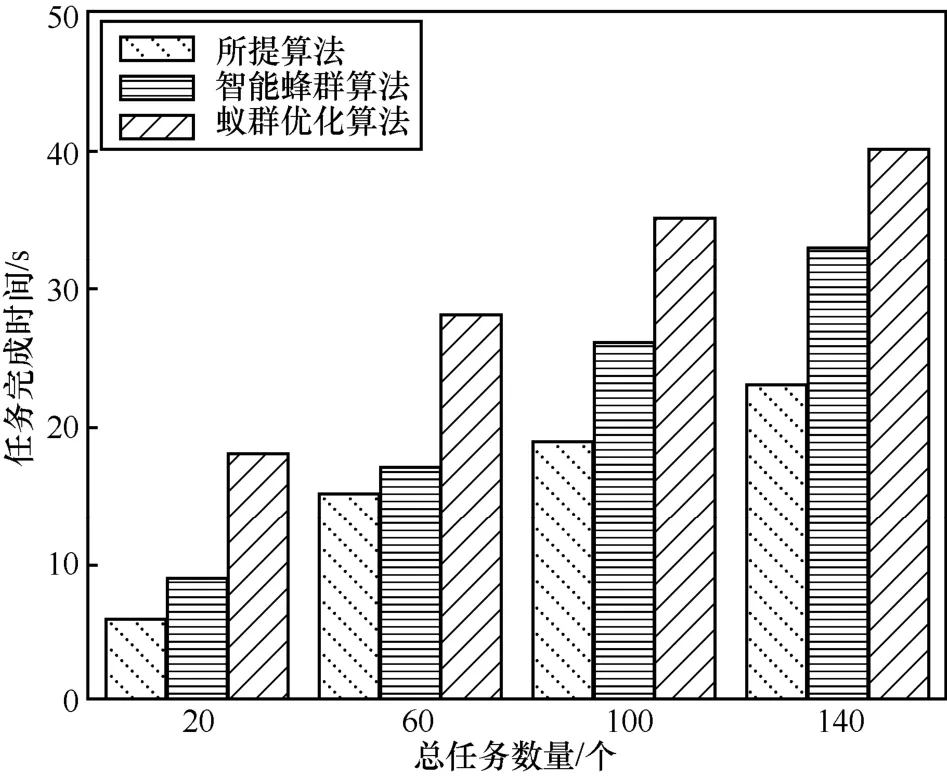
图8 任务完成时间随总任务数量变化关系

5 结束语

卫星通信系统是未来空天地大规模移动网络的重要组成部分，在密集多波束组网过程中，需要在满足用户需求前提下对有限的网络资源进行调度。本文首先分析了密集多波束组网场景下卫星通信系统资源调度的约束条件，建立了多目标优化资源调度模型，然后提出了一种以初始解集构造和额外信息素沉积为核心的改进蚁群优化算法用于求解卫星资源调度问题。仿真结果表明，所提算法在资源调度方面具有良好的敛散性能和优化性能，能够有效地解决密集多波束组网时卫星通信系统的资源调度问题。当然，卫星通信系统的资源调度还会受到其他约束条件的影响，包括大气环境影响、信道干扰等，此类问题有待进一步研究。