基于无标度网络的车联网连通性研究

韩涛，贺威，代俊，左勇，杨旸，葛晓虎

（1.华中科技大学电子信息与通信学院，湖北 武汉 430074；2.国防科技大学电子科学学院，湖南 长沙 410003；3.上海科技大学信息科学与技术学院，上海 201210；4.鹏城实验室网络通信研究中心，广东 深圳 518000）

1 引言

近年来，随着汽车市场规模日益增大，城市道路运载负荷不断加重，导致交通道路运行效率逐渐降低。每年由于交通安全事故造成的人员伤亡事件同样不容忽视。为了提高道路的通行效率及车辆的行驶安全性，实现车与车相互通信的网络——车联网（IoV,Internet of vehicles），已被学术界广泛关注与认可。基于新一代通信网络的发展，车联网的发展有了理论的基础与实现的可行性。车联网作为未来智能交通运输系统（ITS,intelligent traffic system）的重要组成部分，由于链路的连通性低造成信息传输成功率低，车联网的实际应用还有较大的距离，因此提高网络的连通性是学术界和工业界面临的关键问题之一[1]。

近年来，研究人员对高速和城市路段的车联网进行了大量的研究。车联网是通过车辆自组织构建的无线网络通信环境，用来实现道路中车辆与车辆之间、车辆与路边设备之间的单跳和多跳链路通信[2]。车联网中节点之间的相对速度相比于传统蜂窝网络和移动专用网络（MANET,mobile ad hoc network）变化非常显著，导致车联网中节点之间的相对通信距离变化非常快[3]。同时车联网的网络拓扑高频动态变化，车辆之间通信链路建立的随机性较大，网络中节点的链路会由于通信距离和信道的剧烈变化而频繁断连，这对实现稳定可靠的无线传输的车联网产生了严重的影响。

此外，研究人员在车辆的移动性模型和信道模型上对车联网的连通性做了大量研究。文献[4]构建了一个基于细胞单元的移动模型，分析节点密度、传输范围、交通信号灯机制和路障的大小等综合因素对网络的平均链路影响。文献[5]通过部署数量有限的路边单元（RSU,road side unit）来提高车联网的连通性。在城市场景中，研究人员倾向于使用简化的车辆运动模型来分析网络的链路状态，例如，元胞自动机的交通移动性模型[6-7]、跟车模型[8]、随机移动模型[9]和曼哈顿网格道路[10]等。在车联网信道方面，Chandrasekharamenon 等[11]基于排队论提出了一种信道连通性的分析模型，研究了Rayleigh、Rician 和Weibull 这3 种不同的衰落模型下车联网的连通性，但是在信道模型的仿真过程中忽略了车辆作为障碍物对车对车（V2V,vehicle to vehicle）通信的影响。在真实的道路场景中，车与车之间由于存在其他车辆从而导致信道模型的变化。文献[12]通过立体航空摄影收集的高速公路数据集，来测试车辆作为V2V 之间障碍物所带来的信道衰减。结果表明，车辆从视距（LoS,line of sight）到非视距（NLoS,non line of sight）的通信过程中会出现明显的衰减和包丢失。文献[13]在城市和公路场景实际测量的阴影衰减模型中，同时分析了LoS 和NLoS模型在基于Nakagami-m 衰落的信道模型之间的差异，并对路径损耗参数做了精确的测量。文献[14]基于双斜率下LoS 和NLoS 下的路径损耗模型计算网络在不同信道指标下的连通概率，但是其仅考虑所有车辆节点的速度模型为均匀分布的恒速运动，这和实际道路中车辆的运动特性具有较大的差异性。在车联网中，不仅移动特性和信道模型会对网络的连通性造成重大影响，网络中节点之间的通信干扰也会降低网络链路之间的连通性。文献[15]通过将路边单元和移动接入点作为簇头节点，减少了传递的消息数量，降低了网络通信中V2V 之间的干扰，提高了网络的连通性。当前车联网在建立节点之间的链路时，通常考虑节点对其通信范围内的所有节点建立通信链路，然而由于节点在通信过程中存在的相互干扰问题会造成其中的部分链路随机中断，最终车联网的网络拓扑结构呈现随机变化。

车联网链路建立的随机性对网络连通性的影响一直被忽略。车辆在建立链路时，考虑到现实世界中车辆会倾向与能力更强的节点建立链路（获得更高的收益），最终可以有效减少网络中的部分无效链路的建立，提升网络的整体连通性。文献[16-19]揭示了现实中的许多无标度网络，其节点之间的链路分布既不是完全随机连接的随机网络，也不是通过某种规则固定连接的规则网络，而是处于两者之间的中间态。网络中节点与其他节点之间的链路个数称为节点度，通过对网络中节点度的分布分析，如果网络中存在节点度显著大于大多数节点的枢纽节点，且网络中节点度满足幂率分布，那么网络具有无标度特性，统称为无标度网络。在此基础上，研究者进一步归纳和总结了复杂网络理论作为网络科学的理论工具，用于研究具有某种社会行为的网络的拓扑结构。文献[20-21]通过研究德国科隆市一天中3 个时段车辆节点距离的分布来分析网络的链路状态，单从每个时段来看，网络中节点度满足高斯分布，从而得出车联网不具有无标度的特性。文献[22]用瑞士苏黎世的数据信息同样可以得到相似的结论。但是上述文献在分析网络的节点度时未考虑信道模型对链路造成的影响，同时分析网络节点度时，仅仅考虑了单一时间段网络节点度的分布，未考虑车辆在长时间的迭代的影响下具有偏好选择的链路建立对网络的影响。文献[23]提出演化网络模型，将上海和深圳的车辆轨迹作为运动轨迹输入，动态地更新节点的状态，引入无标度网络中BA 模型生长和偏好连接建立链路，经过一定的迭代时间，网络中节点度满足幂率分布。但是其信道采用了简单的单位盘圆（UDG,unit disk graph）模型，两节点之间链路连通状态仅考虑节点之间的距离是否在通信范围以内，未考虑信道对节点度的影响。

综上所述，在分析车联网的链路状态时，当前文献的研究集中在车辆位置、车辆移动模型、网络的拓扑结构和车辆信道状态等单一状态属性，同时缺乏考虑实际通信过程中网络建立偏好连接时对链路状态的影响。本文在考虑双斜率路径损耗、视距和干扰的信道模型下，分析网络中链路的连通概率，有偏好地建立链路，在动态的网络演化过程下构建无标度特性车联网，然后通过其无标度特性提高车联网的连通性。

本文主要的研究贡献如下。

1) 在双斜率路径损耗模型下，车辆通过位置间距信息分析其通信LoS 和NLoS 的概率，考虑车辆之间的相互干扰，在真实网络信道模型下分析节点连通概率，通过马尔可夫链分析节点之间的链路生命周期。

2) 在信道模型下，通过仿真对车联网的节点度进行分析，根据动态的网络演化过程，设计动态生长（DN,dynamic growth）算法，周期性地对网络中的节点进行增加、删除和链路的偏好连接，构建一个无标度车联网，仿真结果验证了模型和算法的可行性。

2 系统模型

本文所考虑的车联网网络体系是基于短距离无线通信（DSRC,dedicated short-range communication）技术在曼哈顿道路移动模型下的V2V 通信。如图1 所示，通过DN 算法对全局链路进行优化，生成的无标度车联网会形成少量的枢纽车辆和大量的普通车辆，其中枢纽车辆具有大量的通信链路，可以作为V2V 通信的中继节点，大多数普通节点仅有少量的通信链路，本文仅考虑V2V 的多跳通信模型。在计算体系中，将车辆节点作为独立的计算单元，对网络链路的连通性进行计算。

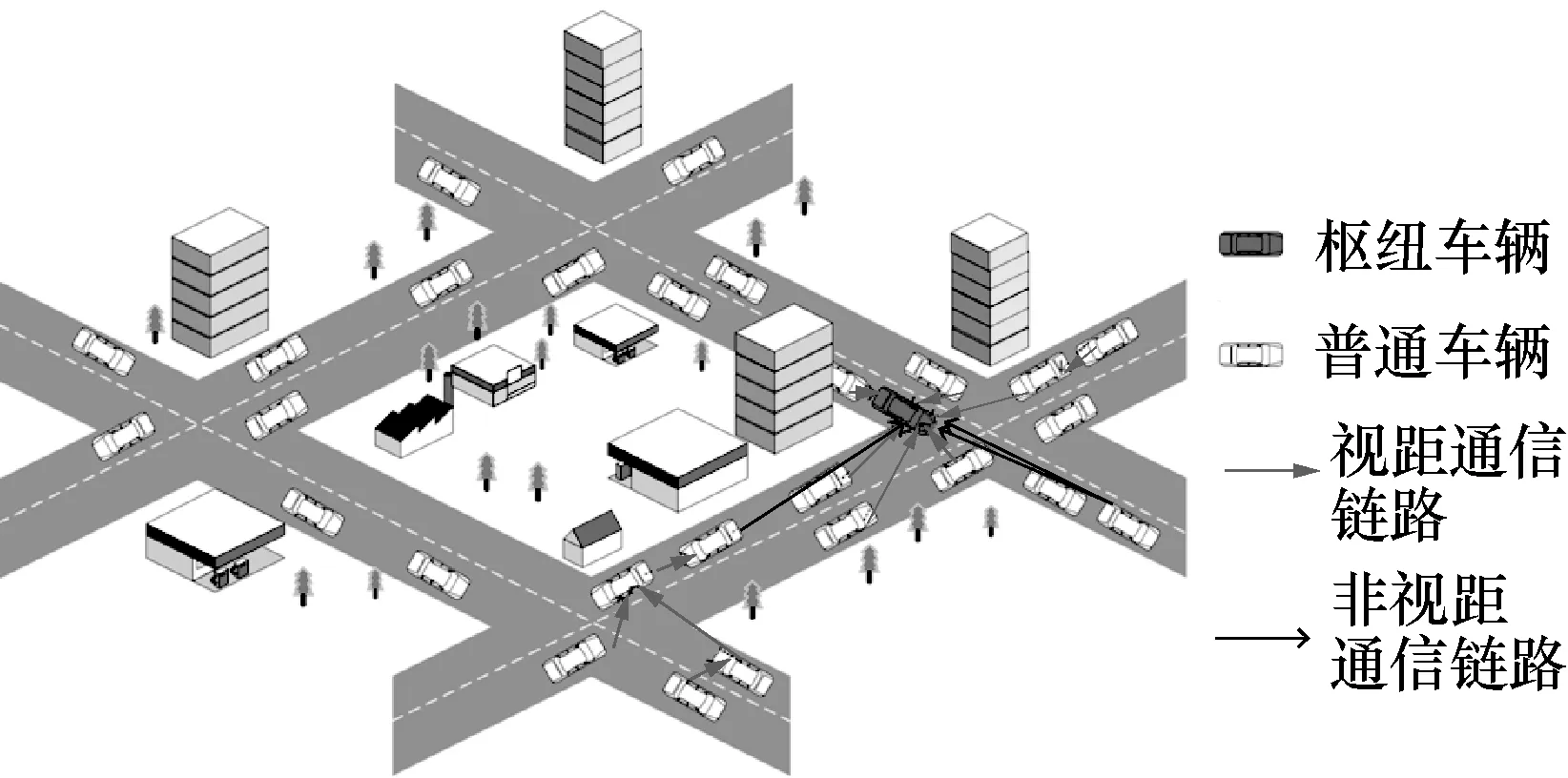
图1 系统模型

2.1 车辆的移动模型

由于车联网中网络拓扑具有高频动态变化特性，节点间的链路状态在衰落和干扰下的通信链路极不稳定。本文将采用基于实测的路测信道的双斜率衰落模型进行建模，建立其链路的连通概率模型。

假设所有车辆具有同样的最大通信距离d0和发射功率tP，基于交通流理论，车流量Q可由道路车辆密度ρ和平均车辆速度V表示，即

通过文献[24]和实际交通数据分析可知，车辆速度在自由态和阻尼态的交通状态下，车辆速度V都服从均值为μ、方差为σ的正态分布，车辆速度的概率密度函数f(v) 可表示为

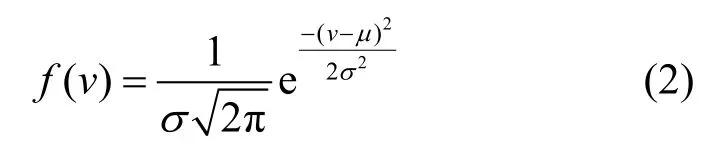
考虑实际情况中车辆的最低速度Vmin=0 且车辆的最大速度满足道路交规所限制的最大值Vmax，故采用截断型的高斯概率密度函数来表示车辆速度，即

假设车辆i与车辆j相距dij，则两车之间的车辆数量取决于车辆的密度ρ，那么车辆的数量Ndij的期望可表示为

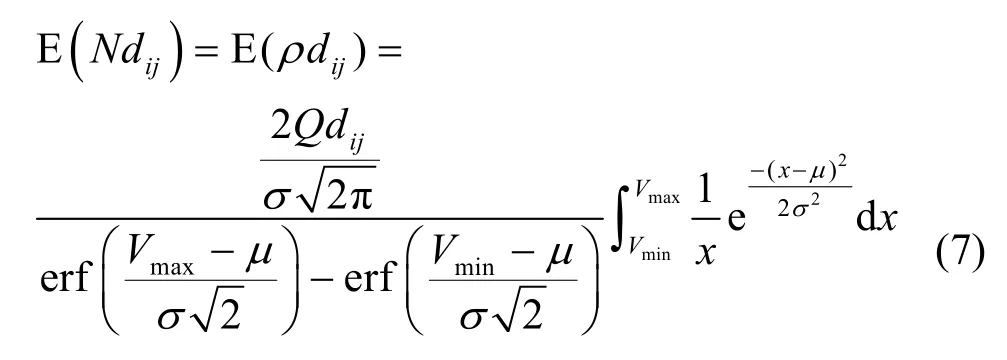
2.2 信道模型（LoS/NLoS）

本文考虑视距通信和非视距通信2 种模式，当两车之间无其他车辆的存在时，即两车之间无其他障碍物的遮挡，车辆之间的通信链路为视距通信（LoS），反之则为非视距通信（NLoS）。由于车辆的高速移动特性，车辆之间的通信链路将在视距通信和非视距通信之间进行转换。本文通过构建一个马尔可夫链的模型来描述这种车辆通信链路转换的状态，如图2 所示。

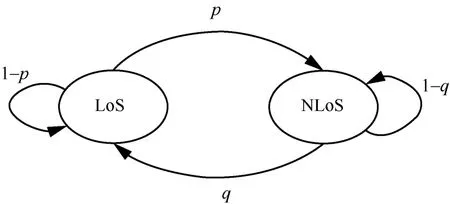
图2 车辆链路在视距和非视距之间的转移

图2 中，状态空间={L oS,NLoS}，其中p和q分别代表了LoS 向NLoS 状态及NLoS 向LoS 状态的转换概率。此时，LoS、NLoS 的状态转移矩阵P为

此时，平稳视距传播为π(LoS)=1 −π(NLoS)。

本文引入文献[12]中真实信道（LoS/NLoS）的路径损耗模型，通过实测高速公路的数据验证，提出一种基于实测数据的双斜率路径损耗模型，相比于传统的无线移动信道建模，基于移动遮挡物的路径损耗模型更加真实地反映了链路的真实情况，其可以表示为

故基于移动模型和信道衰落的连通概率为

2.3 网络的干扰模型

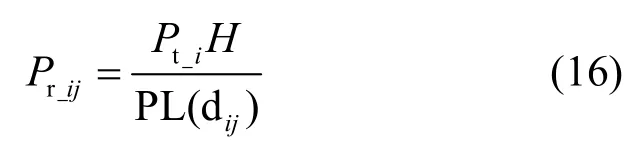
其中，Pti为车辆i的发射功率，H为天线增益。车辆j实际在接收i的信号下的信干噪比（SINR,signal to interference plus noise ratio）为

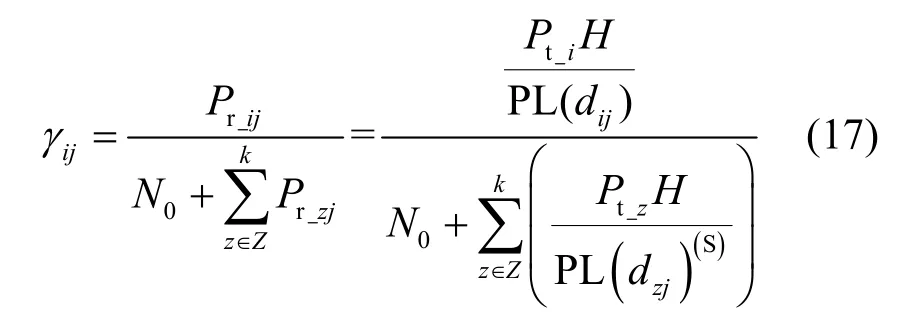
其中，N0为高斯白噪声功率，Pti和Ptz为车辆i和z的发射功率，假设所有车辆的发射功率和天线增益相同，后文发射功率统称为tP，Z为所有对车辆j的干扰车辆集合，为实际的干扰信号功率总和。干扰车辆集合Z的判定原则为假设车辆可使用的总带宽为B，将带宽分为k个子信道，可表示为

当车辆j的邻节点数量L≤K时，通信均处于不同的通信子信道，没有干扰节点。

当车辆j的邻节点数量L>K时，干扰节点集合Z最多包含(L−K)个节点，考虑节点在t时刻传输数据的概率为Pi，此时干扰节点集合为

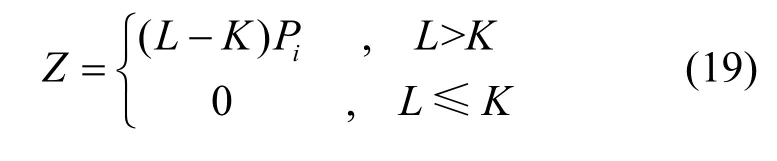
假设车辆的发送功率和天线增益都相同，车辆i的消息可以被车辆j成功解码的概率为

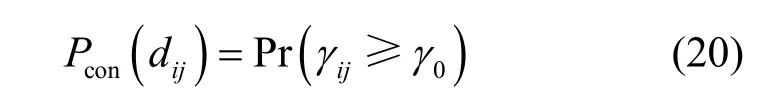
其中，γ0为成功解码的SINR 阈值，当车辆节点信干噪比大于阈值γ0时，链路为连通状态。

2.4 链路的生命周期

链路的生命周期是判断车联网网络连通性的重要指标，其定义为在链路生命周期Tij内，两车辆之间的链路终保持连通状态。设车辆i,j的速度分别为Vi和Vj，两车的初始距离为dk，车辆i,j在第n个时隙的间距d(n)可以表示为

其中，δ为单位时隙，ΔVij为当前时隙的瞬时速度差值。

链路生命周期Tij定义为在前n个时隙状态下，车辆i,j链路始终保持连通，在第(n+1)时隙时，链路断开，此时SINR 小于阈值，即γi,j≤γ0，链路的生命周期可以表示为

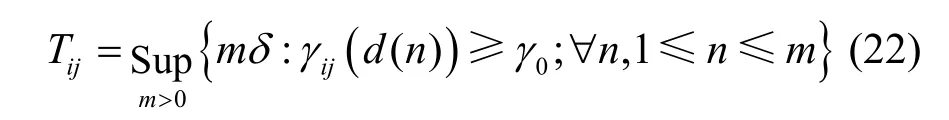
其中，d(n) 为第n个时隙车辆i,j的间距，Sup{⋅}是上确界函数。由于2 个相邻时隙的信干噪比有很强的相关性，不能直接简单地简化为相应时间发生的概率乘积形式。通过将无线信道的状态转移过程构建成Markov 链的形式，故当前状态仅与前一个时隙的状态有关，链路的生命周期的累积概率分布函数可以表示为

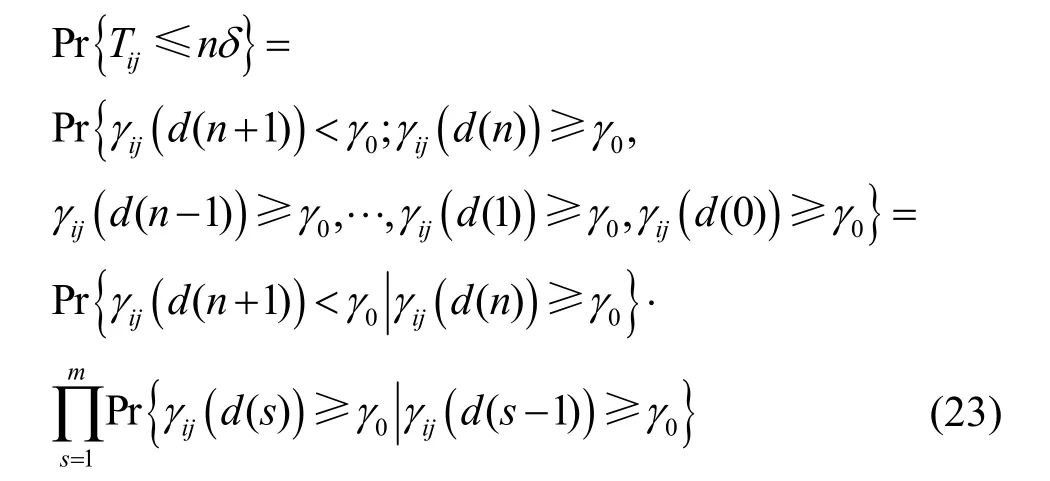
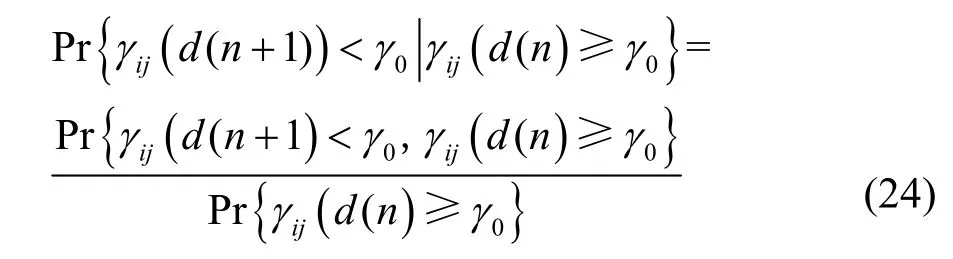
通过对式(24)等号后边的分子进行计算，即

其中，M[t]+=max{t,0}。

同理可知，在式(23)中，链路在第(s−1)时隙连通且在第s时隙依然连通的概率为

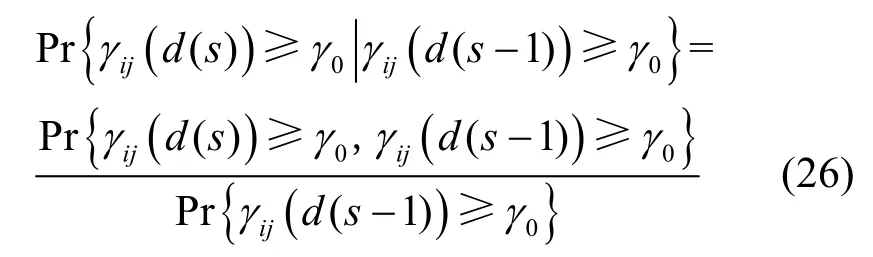
式(26)等号右边的分子可简化为

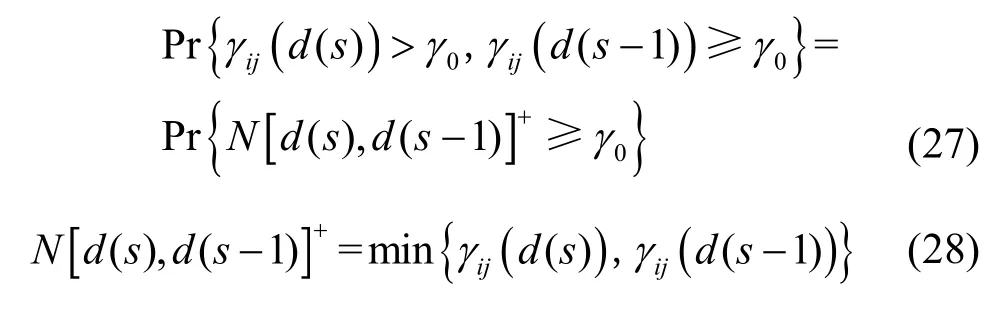
链路的生命周期Tij的概率质量函数可表示为

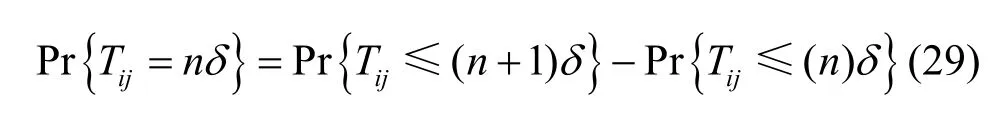
根据链路持续时间的期望，可以得到链路持续的平均时间为

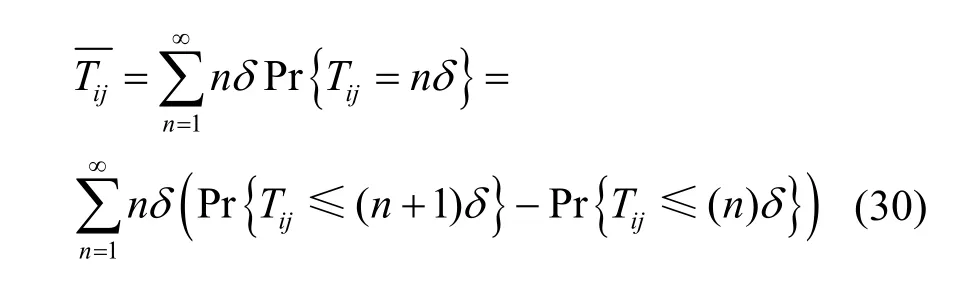
3 无标度网络

3.1 网络属性的关键指标

本节基于网络图来分析车联网的网络属性，并在特定情况下进行比较。

1) 节点度，即该节点和其他节点之间的链路个数。在车联网中，节点度表示该车辆和其他车辆具有可通信的链路个数。

2) 连通性，即网络中节点可以相互通信的节点对的比例。在车联网中，如果两车可以通过一条单跳或多跳路径的通信链路连接，就可以认定为两车连通。

3.2 无标度网络的特征

无标度网络中的无标度体现在“内部缺少标度”，其表示为网络中存在度值相差很大的点，无法通过固定尺度衡量。在不同网络中，节点度值会呈现特定的分布情况。在规则的网络中，网络所有链路按照一定的规则连接，此时节点度为一个固定的常数。在随机网络中，链路完全随机进行连接，节点度通常为泊松分布；在无标度网络中，节点度可以近似为幂率分布

其中，Pk是度值为k的概率，τ为度指数。

无标度网络的特点可以从节点度值的分布得出，网络中存在少部分枢纽节点，其节点度是普通节点的数倍到数十倍。在网络中，大多数节点仅拥有少量链路，但是通过连接少量的枢纽节点，可以将稀疏分离的小网络组建成一个大网络，从而提高网络整体的连通性。

4 无标度网络的车联网构造

从无标度网络中可以发现，在一个生长变大的网络中，当新节点加入网络时，新节点和原网络中的节点建立链路，新节点将有更大的概率与原网络中节点度大的节点建立连接，因为在真实的社会网络中，节点更倾向于与节点度更高的节点（能力更强的节点）建立连接，能力更强的节点意味着该节点可能和其他节点连通的概率更大。在不断增长的网络中，会出现“强者越强”现象，网络中的节点度会趋于幂律分布。

本节通过设计一个DN 算法，对车联网节点进行动态的演化，研究其节点度的分布情况，使网络逐渐向无标度网络演化。本文所设计的DN 算法的详细构造步骤如算法所示。

算法1DN 算法

输入曼哈顿道路模型长度L×L，第2 节的网络信道模型

输出生成当前网络下节点度分布

节点的初始化

在道路上随机设置N辆车节点的初始位置，通过车辆的移动模型对节点的速度进行赋值

网络动态的演化

fort=0,1,2,3…,t0,…

1) 节点的增加

增加M个新的节点

2) 节点的删除

车辆在行驶过程中，离开当前的曼哈顿道路模型的范围，删除该节点C

ifp>pa新的节点进行偏好选择

3) 偏好连接

新增的M个节点与原网络中的N辆车建立偏好连接，其中节点更倾向与节点数高的节点建立链路，新加入网络的节点j选择原网络中的节点i进行连接的概率为

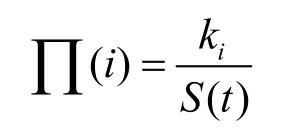
其中，ki为i节点的节点度，S(t) 为车辆j节点所处位置范围内节点度的总和。新的节点进行偏好选择的概率为pa

else ifp>pa新的节点进行随机连接

4) 随机连接

考虑网络在生长过程中的随机性，新节点将以概率pb在已有网络中随机地选取通信范围内的节点建立连接

end if

end for

当网络的运行时隙t=0 时，此时还未对网络进行动态演化，输出的节点度为仅考虑信道的节点度分布，此时节点度为高斯分布；当网络的运行时隙t=t0时，此时节点度为幂率分布，网络演化为无标度的车联网。

5 仿真

本文的具体仿真参数设置如表1 所示。

网络中不同节点数下，节点的连通概率如图3所示。在通信半径相同的情况下，当网络节点数从300 个增加到600 个时，节点的连通概率在相应的通信距离下明显降低，如图3(c)所示，在通信距离为150 m 的情况下，节点密度增加了一倍，对应的连通概率从18.96%下降到12.76%，节点连通概率降低了6.2%。这是因为网络节点在相同通信范围的情况下，由于节点密度的增加，网络中节点间通信由视距变为非视距的概率变大，从而导致信号的路径损耗变大，最终导致连通概率下降。同样地，由于节点密度的增加，节点之间存在的大量干扰节点的概率也更大，干扰信号增大，会降低节点的连通概率。

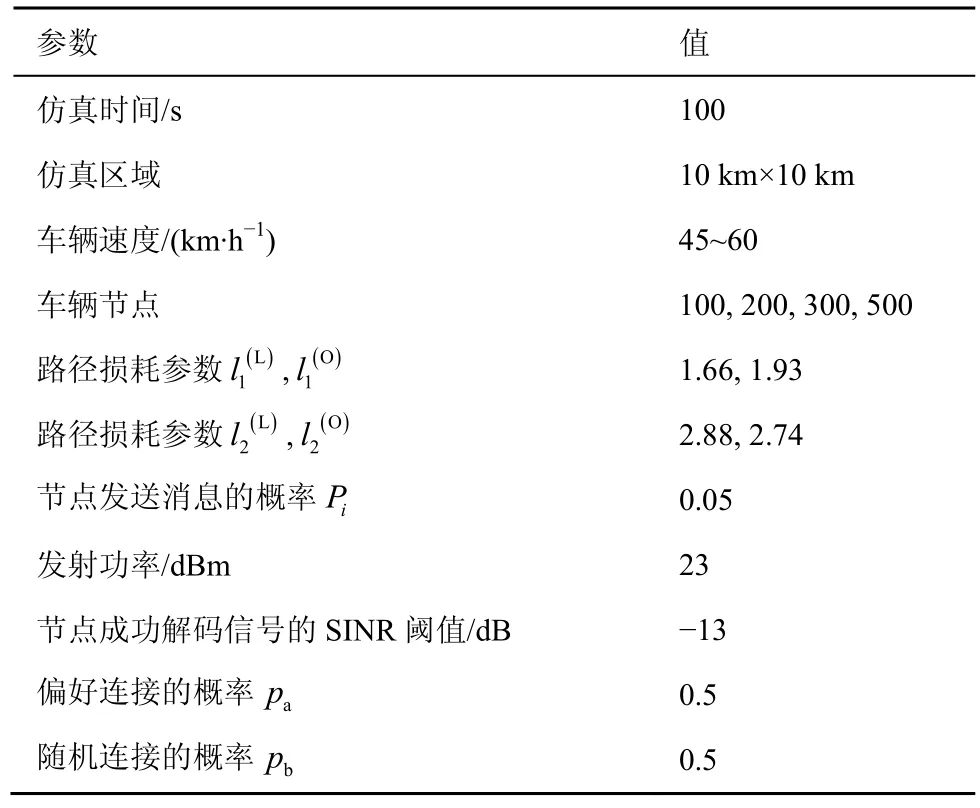
表1 仿真参数设置

图4 分析了在路径损耗模型下和DN 算法下的网络节点度。从图4(a)中可以很明显地观察到，节点度可以很好地拟合高斯分布。车联网在仅考虑信道衰减和节点间的干扰影响下，网络链路的连接和断开是一个随机的事件，网络节点度的分布也是随机产生的，故最终节点度满足高斯分布。而在图4(b)中，节点度可以很好地拟合幂率分布，其拟合的标准差为0.012 73。在DN 算法下，通过有偏好地对网络的链路进行连接，每次迭代一次都会增加节点度值的聚集，通过多次迭代以后，网络中将出现少量的枢纽节点，所以可以看到网络的节点度最终满足幂率分布，同样证明了本文所设计的DN算法可以成功地把车联网演化成具有无标度特性的车联网。

路径损耗模型下和DN 算法下链路的生命周期分布如图5 所示。通过链路的生命周期分布概率来表征网络的连通性，由于车联网的车辆节点在运动过程中，网络中链路之间频繁地建立与连接，因此采用各段链路持续时间与总链路时长比值作为各分段链路出现的概率。从图5(a)中可以看出，节点的55%的链路时长分布在0～10 s，其中所有链路时长超过50 s 的链路总和不到20%。而在图5(b)中的无标度网络中，由于枢纽节点的存在，0～10 s 的链路比例降低了15%，部分短持续时间的链路可以转化为更长时间段的链路，通过计算图5 中链路的期望值可知，DN 算法下的无标度车联网比基于路径损耗的车联网连通概率提高了16%。从图5(b)中还可以看到，由于枢纽节点的存在，网络中各分段的持续时间分布得更加均匀，网络的稳健性也优于路径损耗模型下的车联网模型。

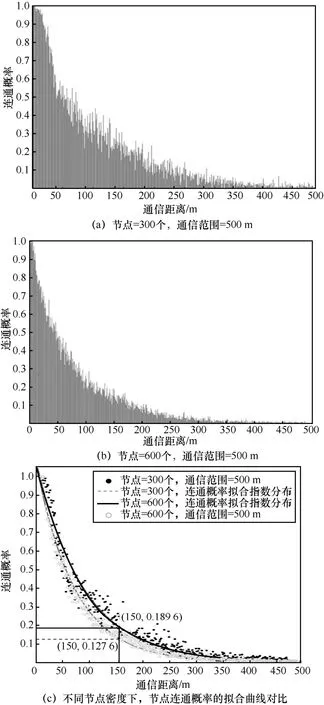
图3 网络中不同节点数下，节点的连通概率

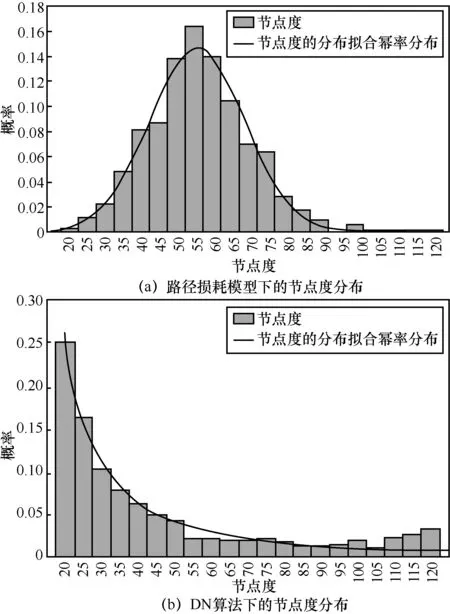
图4 路径损耗模型下和DN 算法下的节点度分布

图5 路径损耗模型下和DN 算法下链路的生命周期分布

6 结束语

在车联网中，由于网络拓扑高频动态变化，车联网在实际通信链路容易频繁地断连。本文首先通过经典的无线通信理论来分析车联网链路的连通模型，分别从路径损耗、视距和干扰3 个因素来考虑链路的连通概率，针对网络在建立链路时未考虑真实网络中的偏好连接问题，本文设计了一个DN算法，动态地增加和删除节点，并通过偏好连接等方式，最终多次迭代使网络演化为无标度网络，由仿真结果可知，网络的整体连通性提升了16%。

将车联网演化为无标度网络以后，由于枢纽节点的存在，如何进行网络的干扰控制，同时通过枢纽节点来构建低时延路由是后续工作关注的重点。