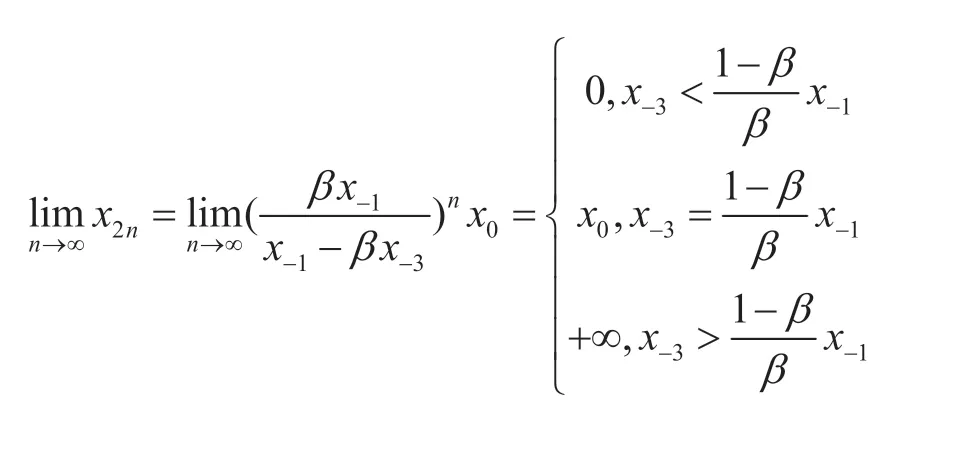一类四阶差分方程的动力学性质

全卫贞 李晓培 曾永均 马秀娴刘林酿 刘秋菊 谌立洋 李 湛 何禄弟

（1.湛江幼儿师范专科学校数学系，广东 湛江 524037；2.肇庆学院数学与统计学院，广东 肇庆 526061）

1 引言

自从Ladas G.等人发表了不少有关有理差分方程的公开问题和猜想[1-4]之后，得到了人们的重视和研究，差分方程的研究由此成了一个研究热点.差分方程的奇点集、振荡解的敛散性和解的周期性、全局性、稳定性等动力学性质也获得了不少的研究成果。[5-13]

在参考文献[3]中，Kulenovic和 Ladas G.研究了下列差分方程，其中p∈R+，初始条件他们得到了下面的定理：

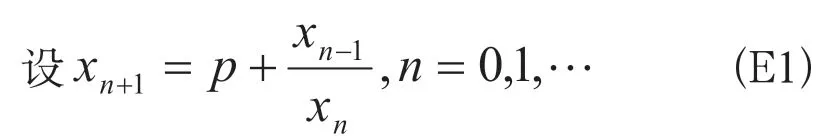
（1）若p=1，则方程（E1）的每个正解收敛于二周期解；

（2）若p＞1，则方程（E1）的每个正解收敛于正平衡点 x = p+1

在参考文献[4]中，Grove E.A.和 Ladas G.研究了差分方程

在参考文献[5]中，本人研究了二阶差分方程

受上述研究的启发，本文我们将研究四阶差分方程

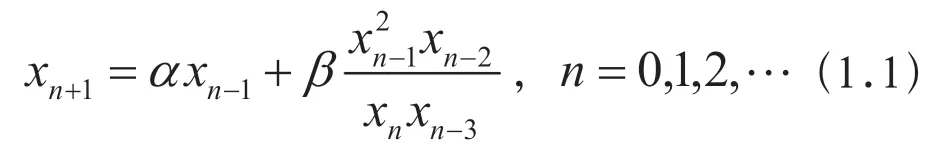
2 预备知识

定义2.1若G 为使差分方程（1.1）的解存在的初始值的集合，则F = R -G 即为奇点集（Forbidden Set).

定义2.2设差分方程

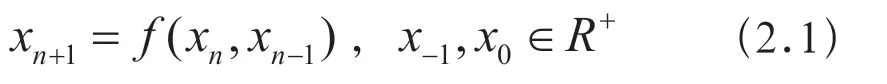
平衡解。

定义2.3称差分方程（2.1）的一个解为终于二周期解，如果存在N ，当

性质2.1设则下列结论成立：

3 主要结果

在本节，我们给出四阶差分方程（1.1）的奇点集和解的渐近性。将四阶差分方程（1.1）整理四阶差分方程（1.1）变为二阶差分方程

定理3.1差分方程（1.1）的奇点集为

故得

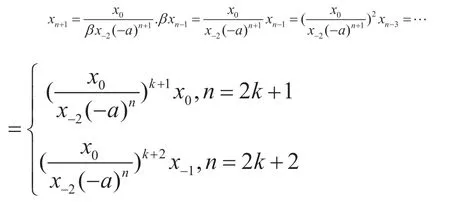
定理3.2当时，差分方程（1.1）的

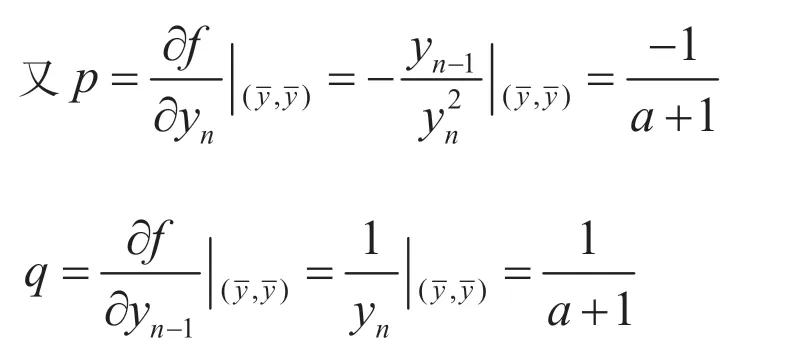
定理3.3当时，设初始值满足则差分方程（1.1）的解

定理3.4当时，则存在常数k ，使得差分方程（1.1）的解满足

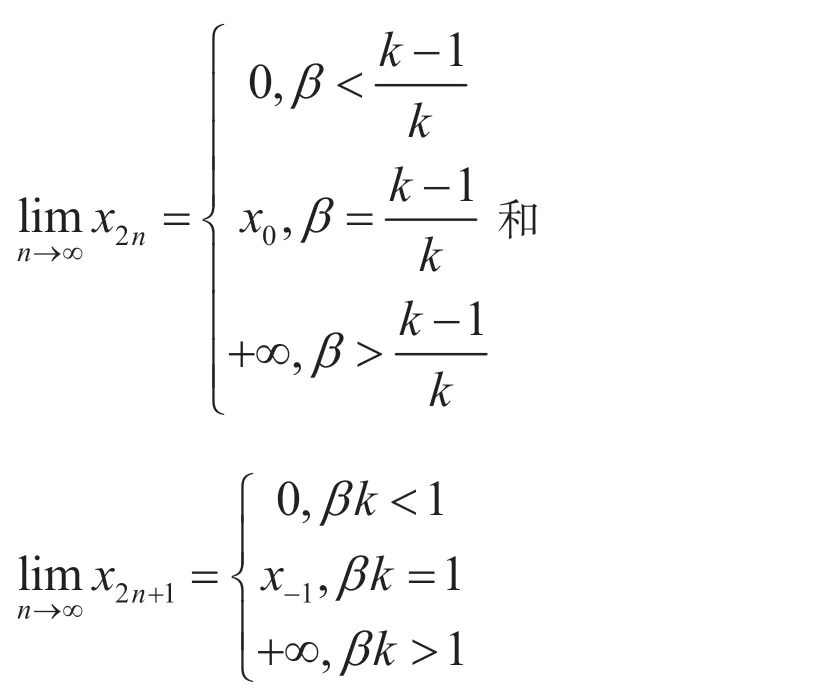
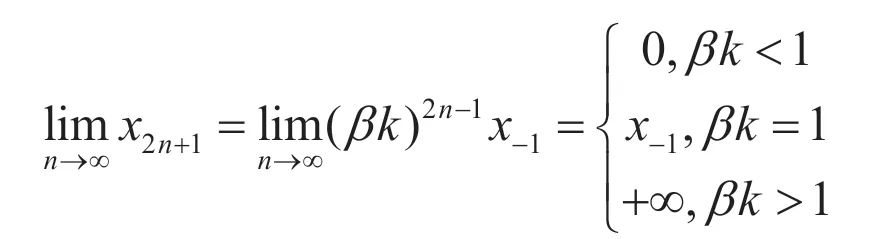
定理3.5当时，若初始值满足则差分方程（1.1）的解和