高中课堂中的数学文化之美

黄养星

摘要：学校里的数学原本是众多理科生甚至文科生喜爱的学科，理科生喜欢数学不足为奇，而文科生对于它的喜爱大多是因为数学文化与中国文化是有共通之处的。在高中数学课堂中，教师可以引导学生感受数学文化中的对称之美。数学文化的意境之美与极限思想的结合具有较强的应用价值和教育价值。在课堂中，教师应该让学生感知到数学文化不是空虚缥缈的，它在生活中无处不在。我们学习数学不仅仅是为了应试，自有它的应用之处、可爱之处。

关键词：数学文化；高中数学；对称；意境；应用

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2021）01-0127

一、探究的意义

数学作为一种文化现象，早已是人们的常识。古往今来，世人总是认为数学是单纯枯燥的逻辑演绎推理。我国许多数学家为了将数学文化从这样的怪圈中挣脱出来做出了巨大努力，如孙小礼和邓东皋等合编的《数学与文化》，汇集了一些数学名家的有关论述，也记录了从自然辩证法研究的角度对数学文化的思考。齐民友的《数学与文化》，主要从非欧几何产生的历史阐述数学的文化价值，特别指出了数学思维的文化意义。郑毓信等出版的专著《数学文化学》，特点是用社会建构主义的哲学观，强调“数学共同体”产生的文化效应。这些著作重点是分析数学文明史，充分揭示数学的文化内涵，肯定数学作为文化存在的价值。在高中数学教学中，大多数教师只注重数学知识和数学解题技巧的传授，而忽视数学文化。

二、探究的方向

以下笔者将简短地从一些解题角度中，简单展现数学在高中数学学习过程中的文化渗透。

和所有文化现象一样，数学文化直接支配着人们的行动。数学文化在所有文化中显得尤为孤立，既拒人于千里之外，又孤芳自赏，令人更加觉得数学枯燥怪异无趣。而事实上，学校里的数学原本是众多理科生甚至文科生喜爱的学科，理科生喜欢数学不足为奇，而文科生对于它的喜爱大多是因为数学文化与中国文化是有共通之处的。

三、探究数学文化的对称之美

数学文化与中国文化有共通之处，而数学与文学的思考方法更是相通的。举例来说，中学课程中有对称，文学中则有对仗。对称是一种变换，虽进行了一系列平移旋转但性质保持不变。对仗是上联变成下联，但是字词句的某些特性不变。如“春种一粒粟，秋收万颗子”“两个黄鹂鸣翠柳，一行白鹭上青天”“千里冰封，万里雪飘”等句，均有对偶手法出现，不仅言简意赅，而且朗朗上口，用简单的数字来叙事，更是体现了数学与文学的融合之妙。在几何中，轴对称和中心对称是最直观的对称，现将轴对称与中心对称的异同列表如下：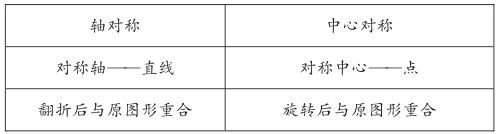

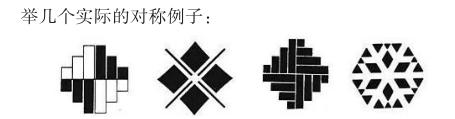
在上列图形中，可以直观感受到对称之美，与诗句的对称比起来毫不逊色。在高中数学课堂中，教师同样可以引导学生感受数学的文化之一：对称之美。

函数是高中数学学习过程中十分重要的一个环节，在讲授函数图像的课时中，教师也可以引导学生将函数的周期性看成对称性，因为周期函数的图像是无限延伸的曲线，平移后可与自身重合，整体不变，在画图时显得尤为流畅，最典型的例子是三角函数。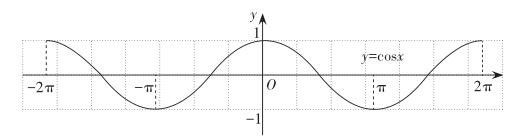

实践证明，学生在学习三角函数这一阶段，确实对三角函数图像记忆深刻，这就得益于三角函数图像的周期性和对称性，在前期有了对称图形的直观感受，再顺其自然接受了函数图像的对称性，学生可进一步更深层次地感受到数学课本中来自图形和数字的灵魂，而图形和数字的灵魂实则就是数学文化。

在数学公式中也有许多具有对称性的例子，最简单易懂的完全平方公式：（a+b）2=a2+b2+2ab，a与b是可以互换且地位平等的。可以说，在高中阶段，没有比它更容易记忆的数学公式了，有了对称的辅助作用，学生对于公式的理解如虎添翼，障碍全无。

四、探究数学文化的意境之美

学生自小学习汉语言文学基础，朗读背诵一篇篇古诗词，不难发现，自古以来，中国文人在文字中孜孜不倦地追求一种意境之美，也有不少学生对其兴趣浓厚，在平时写作时效仿临摹，以求产生不俗的效果。我国的文学文化影响了一代又一代的青年人，但是在数学文化中，其实也蕴含着丰富的意境之美。学生念在嘴边的名句“孤帆远影碧空尽，唯见长江天际流”，体现在数学上，正是极限概念。我们在学习高中数学时，时常有机会接触到与极限思想有关的解题思路，只不过囿于题海时常会忽略。其实，这样的题是可以信手拈来的。如下列这道题：

五、探究數学的应用之美

在生活中，背诵的语文诗词看起来和数学毫不相关，其实有着千丝万缕的关联。唐朝诗人王之涣在《登鹳雀楼》中写下了脍炙人口的诗句：“白日依山尽，黄河入海流。欲穷千里目，更上一层楼。”要想看到千里之远，就要登上更高的楼层，那么诗人所说的更上一层楼到底需要多高呢？我们可以用数学思维解决这个问题。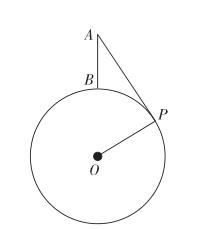

我们把地球看成一个圆，半径OP=6370km，PA为切线，所以OP垂直于PA，PA=500km，勾股定理求得AB=19.593km，约等于5937层楼。事实上这是一道简单的直线和圆的数学应用题。

诗句描写了诗人想探求无止境的美好愿望，如果在数学中加以应用，我们除了能感受诗词的美好意境之外，更可以借助数学思想和数学方法追求真实，如此，诗歌的想象就和数学的精确相映成趣，而这样的结合在生活中是应用广泛，并且不可或缺的。所以在课堂中我们更应该让学生感知到数学文化不是空虚缥缈的，它在生活中是无处不在的。我们学习数学，不仅仅是为了应试，也为了最初始的对于文化的向往和追求。数学文化这一概念，在课堂外，在生活中，自有它的应用之处、可爱之处。

六、总结

通过几组浅显的探究案例，我们发现数学文化也是社会文化的重要内容，与中国传统文化思想结合起来能够提高学生的主观能动性，提高学生的数学素养，进而影响学生的思维方式和思维能力。同时，数学文化能够使人们体会数学的内涵和数学的魅力，在看待世界思考问题时能结合数学思想，把对数学的感性认识上升到理性认识。

数学的对称之美教会学生在看待问题时能够加强变与不变的认知，不去一味地追求一成不变，如果能在日常解题时融入对称思想，或许能激发学生灵感，事半功倍；数学的意境之美又提醒教师，在时间允许的情况下，课堂上也不能只知赶进度不知旁征博引；另外，如果把极限的思想渗透到高中数学课堂，学生不仅对解题方法多了一重认知，对数学文化的认识也能更加透彻，可以说有百利而无一害。教师在教学时加入数学发展历史和数学本质知识的讲解会深化学生对数学概念的理解，而教师在渗透数学文化思想时应注重与学生思想的交流，要积极解读学生的面部表情、肢体语言，感受学生的接受态度和接受程度，并引发学生对数学文化的思考，从而培养学生对数学文化的兴趣，实现课堂上的思想统一。

参考文献：

[1]谢锦辉.文化与高中数学学习[M].广州：广东高等教育出版社，2017.

[2]郑毓信，王宪昌，蔡仲.数学文化学[M].成都：四川教育出版社，2001.

[3]孙小礼，邓东皋.数学与文化[M].北京：北京大学出版社，1990.

（作者单位：江苏省泰州市姜堰区娄庄中学225500）