大兆瓦风电主轴承多工况载荷谱编制
2021-05-12戴莉斯胡兴涛肖夏
戴莉斯,胡兴涛,肖夏
大兆瓦风电主轴承多工况载荷谱编制
戴莉斯,胡兴涛,肖夏
(1.四川省机械研究设计院(集团)有限公司,四川 成都 610031;2.四川航天烽火伺服控制技术有限公司,四川 成都 611130)
风电主轴承进行台架疲劳寿命试验时,实际工况下测得的原始载荷数据频率变化太快,无法直接在试验台加载,有效处理原始载荷数据并制作成便于试验台加载的轴承载荷谱是整个疲劳试验的基础,也是疲劳寿命估算的理论依据。以某型号2.5 MW 风电主轴承为例,进行了一种全新的多工况全载荷轴承载荷谱的编制。通过从单一工况延展到多种工况,由一种载荷合并为全载荷,编制方法的核心是雨流计数法统计原始载荷,再利用威布尔三参数方程扩展已知数据,最终得到了该型风机主轴承在30种工况下的10级实验载荷谱。本载荷谱既保留了原始数据的基本特征,又简化了加载方式,使得轴承试验加载成为可能。
风电主轴承;载荷谱;雨流计数法;威布尔分布;多工况载荷
开发新的可再生无污染绿色清洁能源是解决当今能源和环境问题的主要方向和手段[1],风能作为一种清洁的可再生能源,越来越受到世界各国的重视,风力发电行业也随之被各地区和国家大力提倡和发展,其中,轴承尤其是变桨、偏航和主轴承等关键零部件的设计制造是风电机组的核心技术之一[2]。
风力发电机的主轴承是叶片和轮毂的连接部件,其工作环境恶劣,在使用过程中要承受大小和方向均不规律变化的载荷,且主轴承要求有20年以上的使用寿命。在计算主轴承的寿命及静承载能力时,需用到当量动载荷和当量静载荷[3]。实际工况下采集得到的轴承原始载荷数据为时间历程载荷,即载荷循环随时间变化的分布情况,但由于采样数据与实际载荷有一定偏差,并且试验台的液压加载系统往往不能达到与原始载荷相同的变化频率,因此无法将采样数据直接用于零件疲劳寿命预测、设计和试验。为此,重新进行零件的工作载荷编谱,能够更全面准确地反应工作载荷特性,也更易于对零件进行设计和试验[4]。
轴承所受载荷分为力和力矩,且分不同方向。一般轴承载荷谱只针对单一工况或者单一载荷,无法兼顾多工况多载荷的情况,与实际轴承所处工况不一致。由此,本研究以某型号2.5 MW风电主轴承为例,通过雨流计数法与威布尔分布法结合,处理以及拓展原始载荷数据,由得到的单一工况下的载荷谱通过时间加权系数生成全部30种工况下的载荷谱,再把各种载荷的载荷谱通过分级加载的方式融合成一个全工况等效载荷谱。
1 雨流计数法处理原始载荷
1.1 原始载荷的选择
此型号风机主轴承为双列圆锥滚子轴承,实际工况下的受力情况如图1所示。
本次计算采用的试验数据包含30种工况,每组工况有10 min试验载荷,共计20万组数据。每组数据包括时刻点、转速、轮毂处的F、F、F、M、M、M等数据。如表1所示。
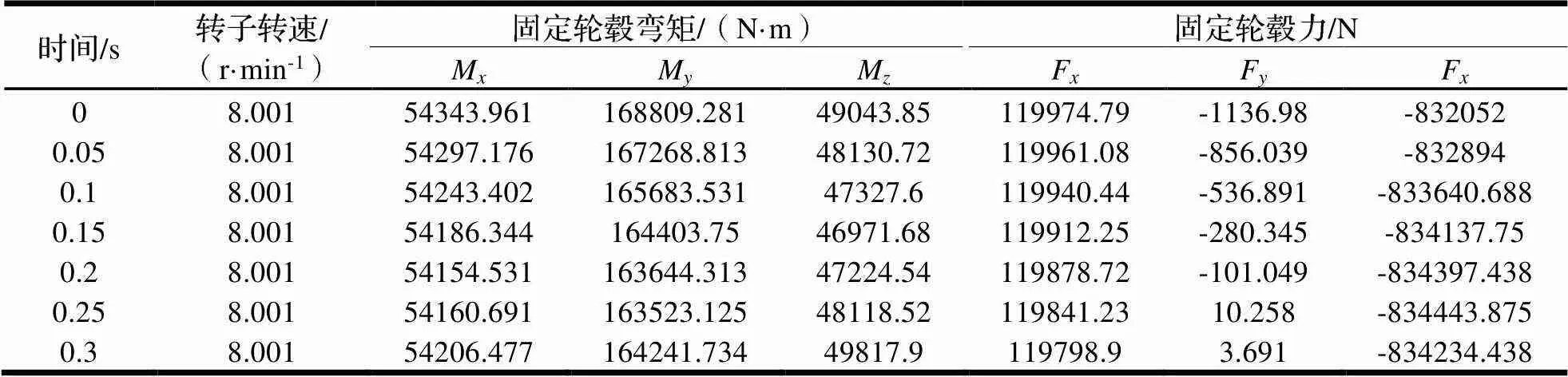
表1 原始统计载荷
1.2 雨流计数法处理数据
原始载荷通过雨流计数统计得到载荷不同大小的幅值及均值的循环作用次数[5]。以计算F为例,将已知的第一组工况载荷表的F提取出来,根据雨流计数法的计算法则,对其编程并导入MATLAB软件中进行计算,结果如图2所示,其中方向为幅值变化分布级,方向为均值变化分布级,方向为在特定幅值和均值载荷级下的循环次数。

图2 雨流计数法计算结果(三点循环计数运算逻辑)
分别对载荷幅值和均值进行叠加,可分别得出50个载荷幅值和均值等级的循环数,如图3所示。
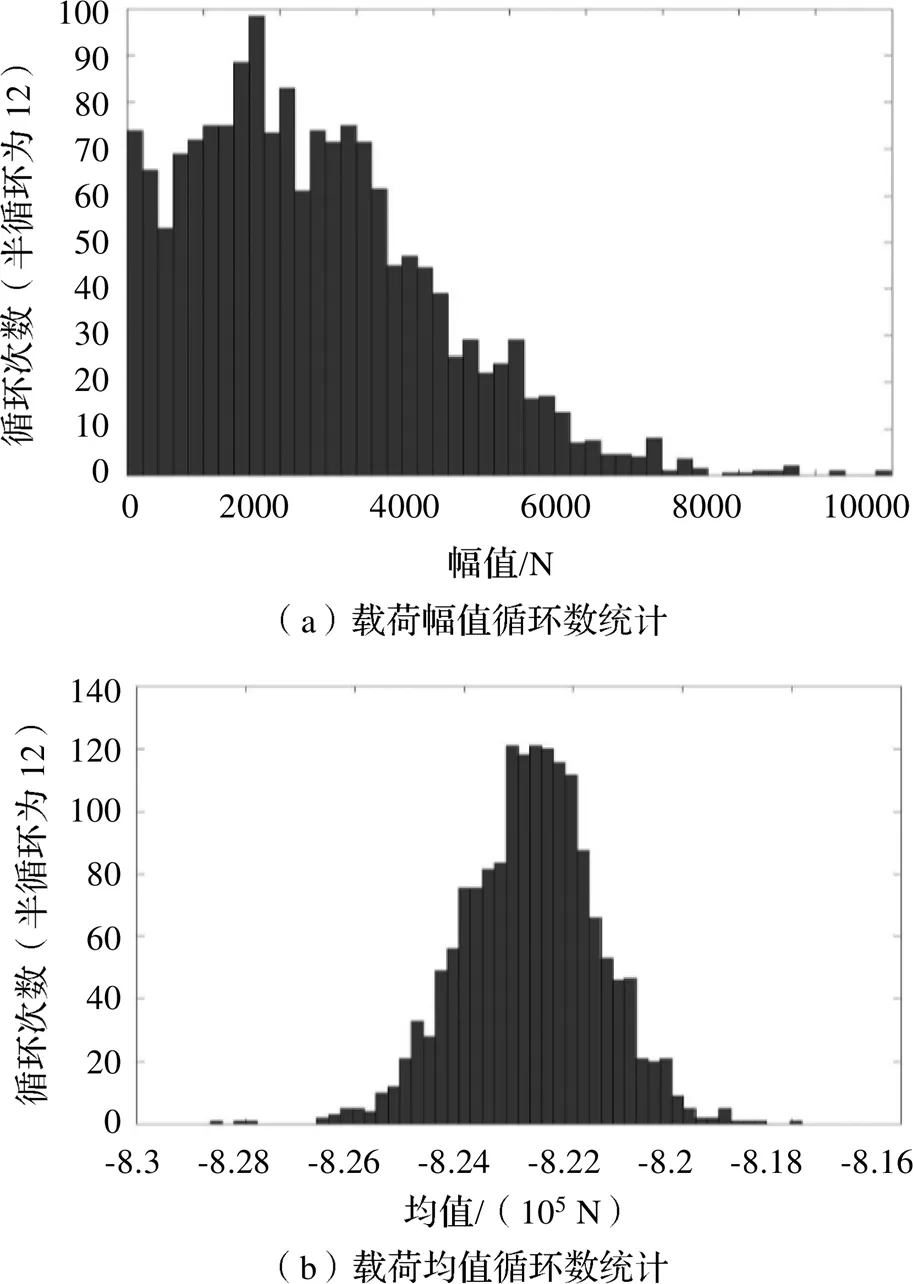
图3 统计直方图
由图3可知,载荷幅值统计近似符合威布尔分布,均值载荷统计近似符合正态分布。
2 单工况载荷谱的编制
2.1 载荷幅值和均值的分布函数
对随机载荷的统计分布,可以将载荷幅值和均值视为二元随机变量,用二维概率分布来描述载荷幅值和均值的联合分布[6]。其二维联合分布函数为:
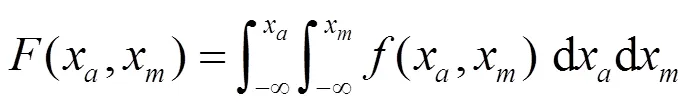
为了求得载荷幅值和均值的二维概率密度函数,首先要对幅值和均值的两个边缘分布进行估计和检验,然后再考虑两者之间的相关性。考虑到风电载荷的特殊性,本研究将载荷幅值分布作三参数威布尔分布检验、均值分布作正态分布检验,然后根据其相关系数的大小确定一种合适的分布函数。
(1)设幅值x服从三参数威布尔分布,其概率密度函数为:

式中:为形状参数;为位置参数;为尺度参数。
(2)设均值x服从正态分布(,2),其概率密度函数为:
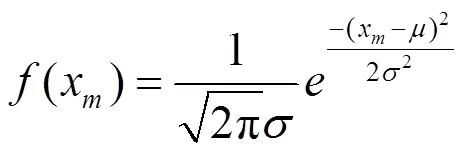
式中:为形状参数;为位置参数。
2.2 幅值概率密度函数和均值的波动中心
二维载荷谱描述的是载荷幅值、均值与频次的关系,一维载荷谱描述的是载荷等效幅值与频次的关系。将随机载荷的幅值和均值视为二元随机变量比较接近实际载荷,但目前在实际应用中,国内外常采用“波动中心法”将疲劳载荷简化为一维随机变量进行统计处理[7]。波动中心就是所有参加统计的载荷循环均值的总平均值,以波动中心作为载荷循环的静力成分,幅值作为动力成分,将幅值叠加到波动中心之上,从而不考虑载荷均值的分布,只考虑载荷幅值的分布。
总的均值即波动中心为:
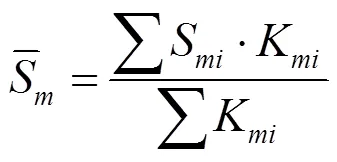
式中:S为载荷均值的分组均值;K为对应分组均值的频次。
经过雨流计数法处理后的F数据为包含均值与幅值的雨流矩阵,结果如表2和表3所示。
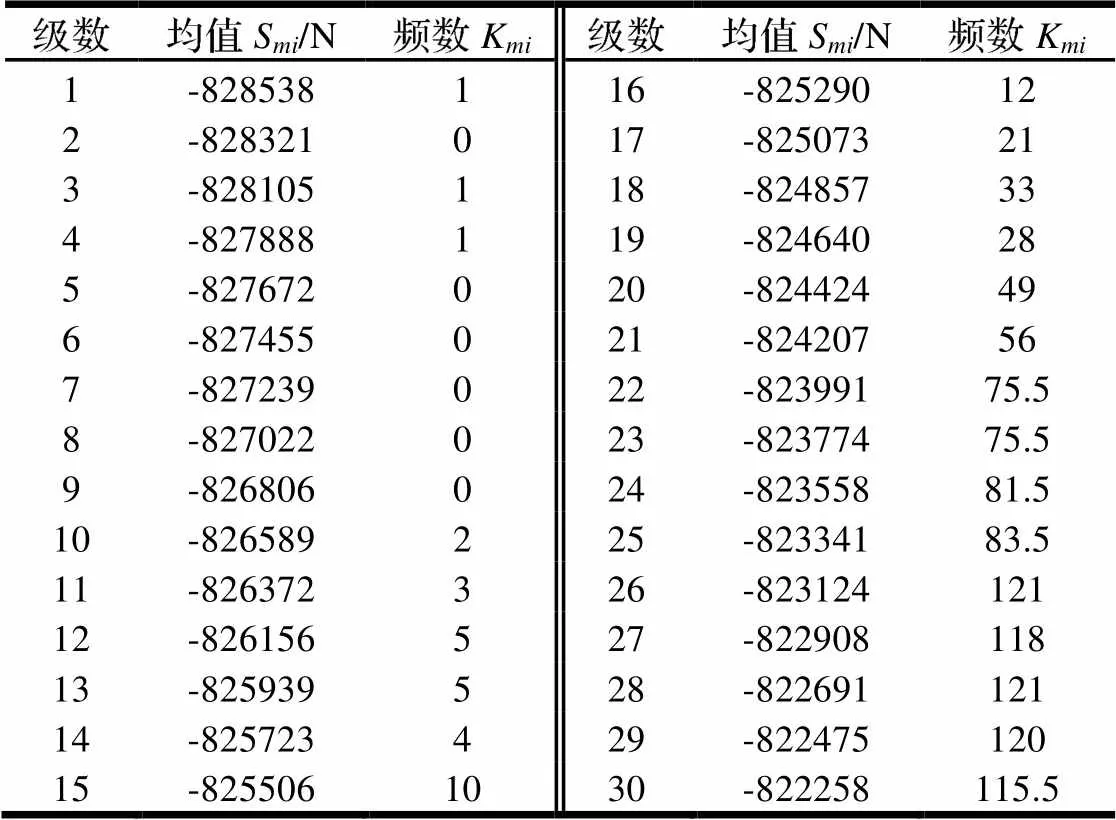
表2 Fz的均值统计表
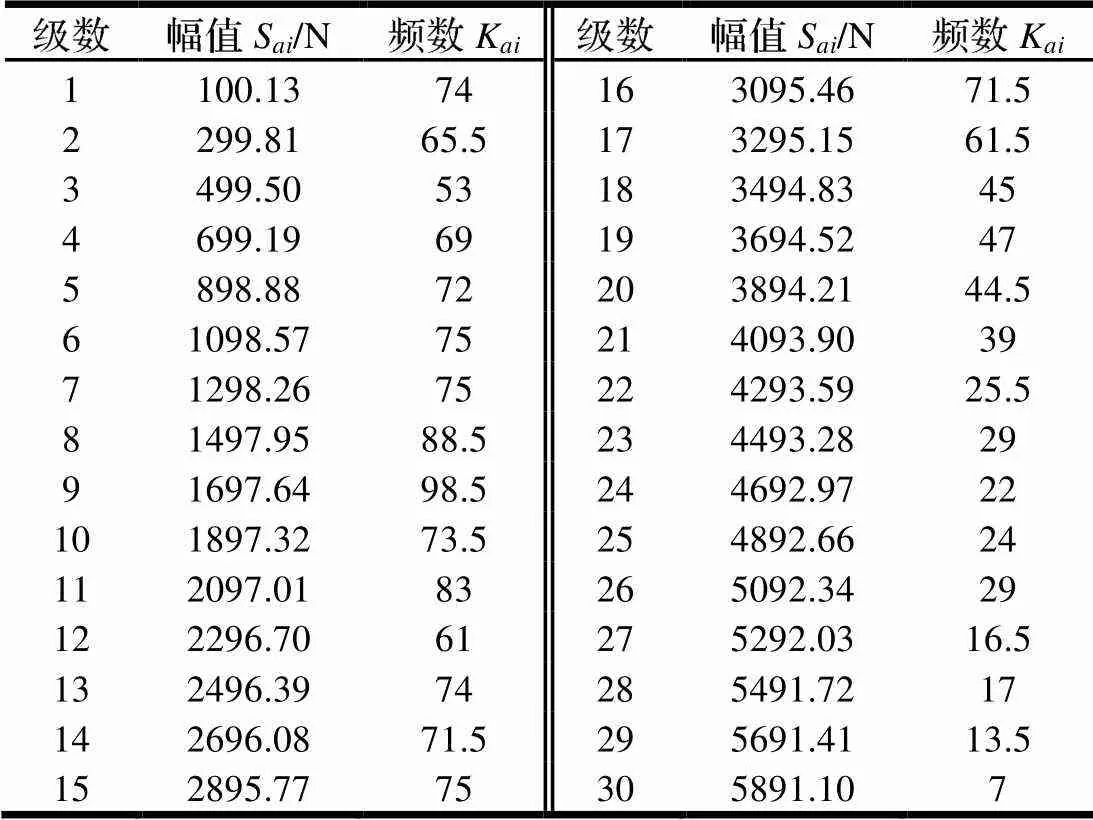
表3 Fz的幅值统计表
由式(4)和表2计算得第一种工况均值的波动中心载荷为:S=822 kN。
根据极大似然法计算载荷幅值的威布尔三参数分布的三参数[8-9],通过MATLAB编程和表3的载荷幅值的威布尔分布三参数为:=3、=2574.1、=1.47。
由式(2)可得幅值x概率密度函数为:
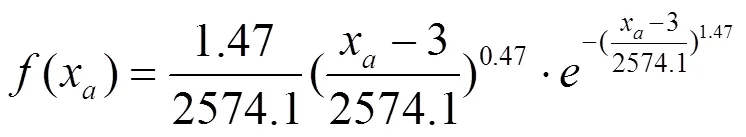
其概率密度函数的曲线图如图4所示。

图4 第一种工况Fz幅值威布尔分布曲线
2.3 计算载荷幅值的极大值
为了获得载荷谱时间内的累积循环次数、得到累积频数曲线,本研究采用概率密度法分别计算各工况各自扩展到106次循环次数而得到各载荷工况下的幅值和均值的极值,然后根据多工况复合概率密度函数得到多工况下全寿命载荷扩展的载荷最大值。
根据材料力学可知,通常认为在机械零件整个工作寿命期间应力变化次数小于103的通用零件,均可按静应力强度进行设计。此处,循环次数约为103以前,使材料试件发生破坏的最大应力值基本不变,因此可以将应力循环次数≤103时的变应力强度看做是静应力强度的状况[10]。
本文认为累积频次为106次时,频次为103次的载荷幅值为引起疲劳破坏的载荷幅值的极大值。由超值累计频率函数计算得到幅值载荷极大值max:
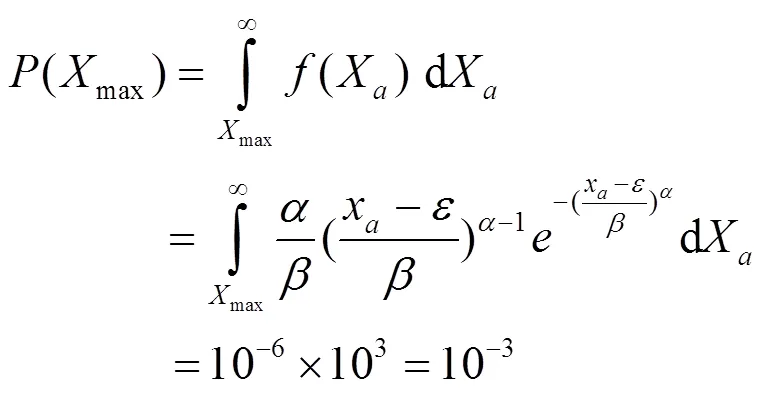
代入参数后解得该工况的幅值极大值为:
max=122 kN
2.4 一维载荷谱编制
用不等间距法将幅值载荷分为10级,各级载荷幅值与最大载荷幅值的比例系数为:1、0.8、0.7、0.6、0.5、0.4、0.3、0.2、0.1、0,即可分别得到10级载荷幅值X的大小。将各X代入式(7)求解出N,然后根据式(8)求出载荷幅值对应的循环次数。表4为第一种工况幅值的10级载荷谱。


式中:N为第级载荷循环次数。

表4 第一种工况Fz载荷幅值一维10级载荷谱
3 多工况载荷谱的编制
3.1 加权系数
对多工况的风电载荷,在求出各工况下疲劳载荷谱的分布概率密度函数之后,可根据各工况的加权系数合成多工况的复合概率密度函数。为此需要知道各工况的载荷时间历程以及各自所占的比例,如表5所示。
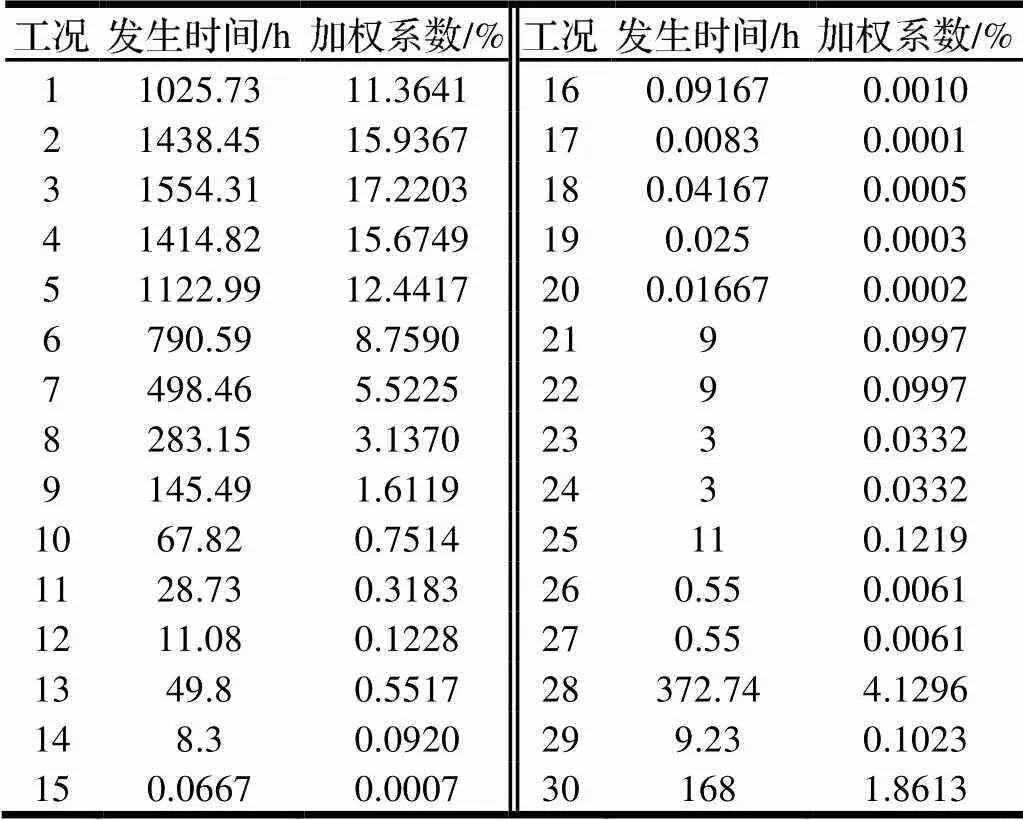
表5 Fz所有工况的载荷发生时间(一年内)
3.2 载荷均值的总波动中心
确定载荷均值的总波动中心,为:

式中:k'为第种工况载荷均值的加权系数;x为第种工况载荷均值的波动中心。
各工况的波动中心如表6所示。
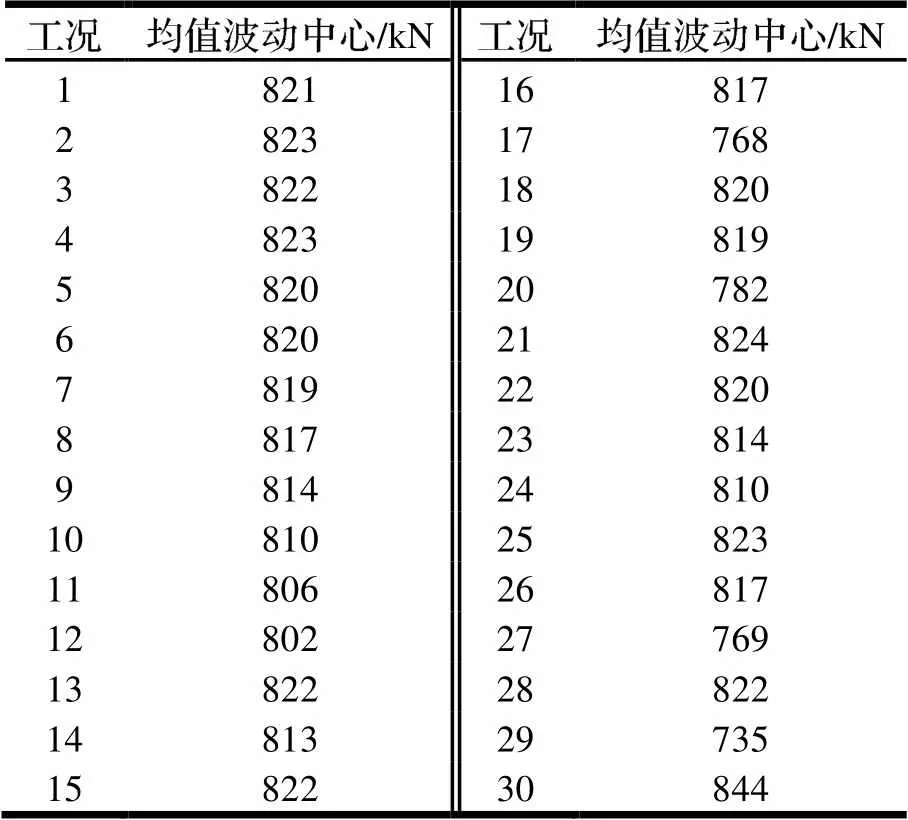
表6 Fz各工况载荷均值的波动中心
通过式(9)求得均值的波动中心为:
X=821 kN
在风电轴承疲劳实验中,把所有工况的载荷均值波动中心作为载荷和幅值一维载荷谱叠加作为实验载荷谱。
3.3 多工况载荷幅值极大值
在2.3中介绍了单工况载荷幅值极大值的计算方法,通过上述方法同样计算出多工况载荷幅值的极大值,取复合概率密度的累积频率
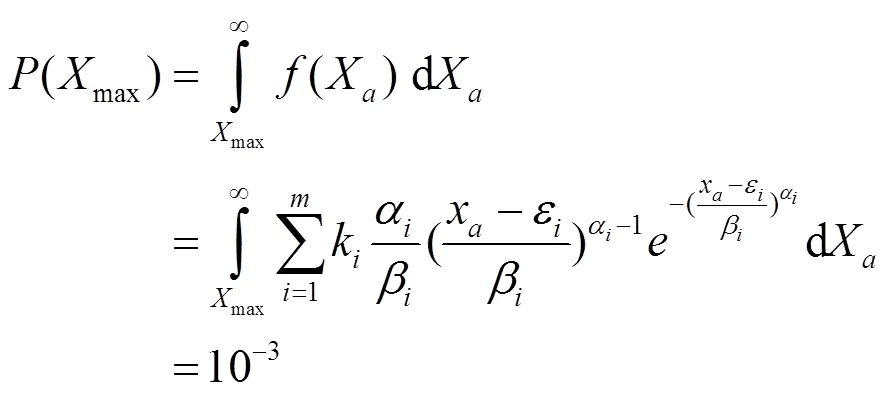
式中:α、β、ε为每种工况下的威布尔分布的三个参数;k为第种工况的加权系数。
计算结果如表7所示。
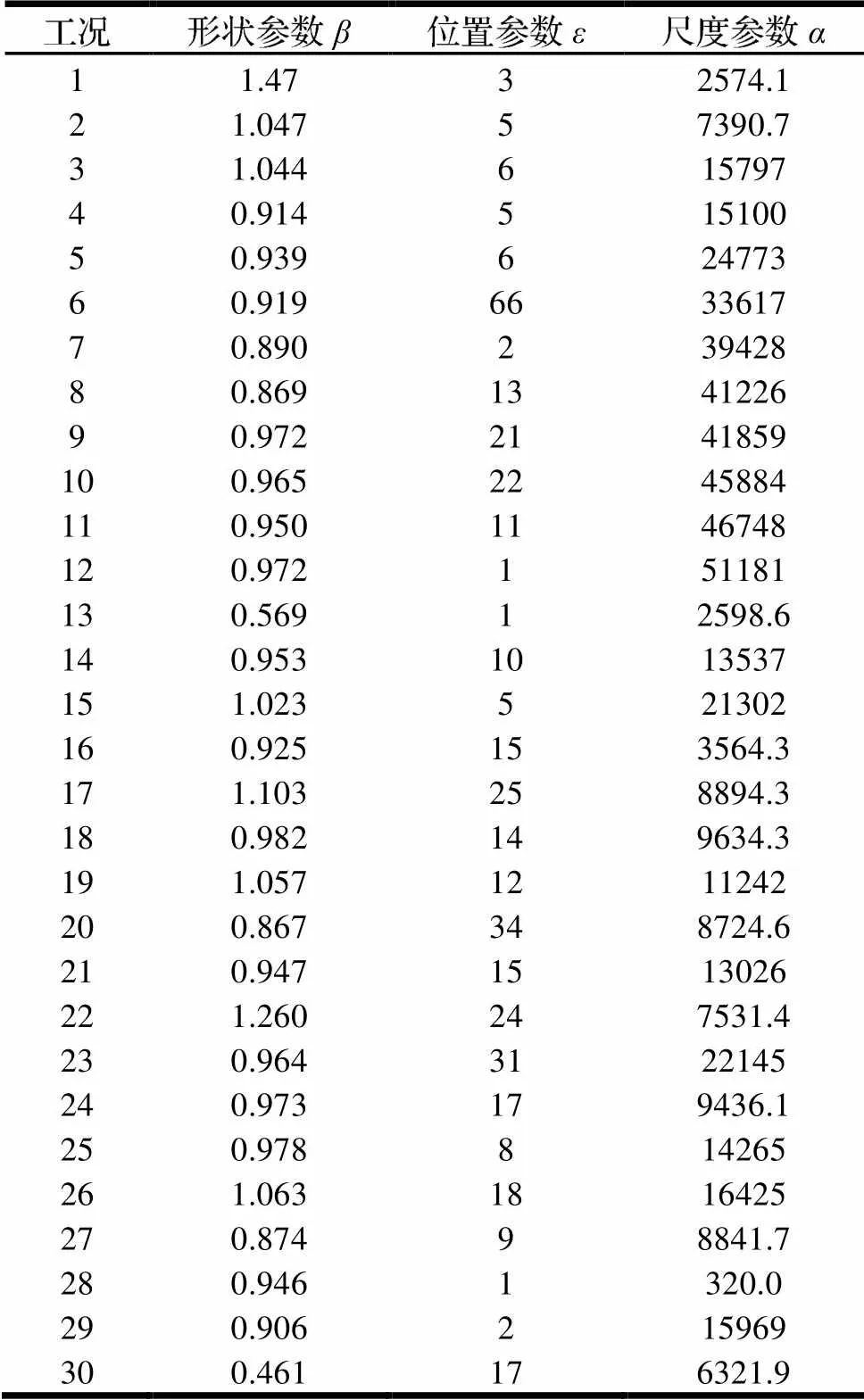
表7 30种工况载荷幅值的威布尔分布参数
将表7的值代入式(10),用MATLAB软件求解得:
max=108 kN
3.4 载荷幅值的分级
得到幅值极大值后,同样采用不等距法将其分为10级,然后利用式(7)求出载荷幅值对应的循环次数,即可得到所有工况幅值载荷谱,如表8所示。
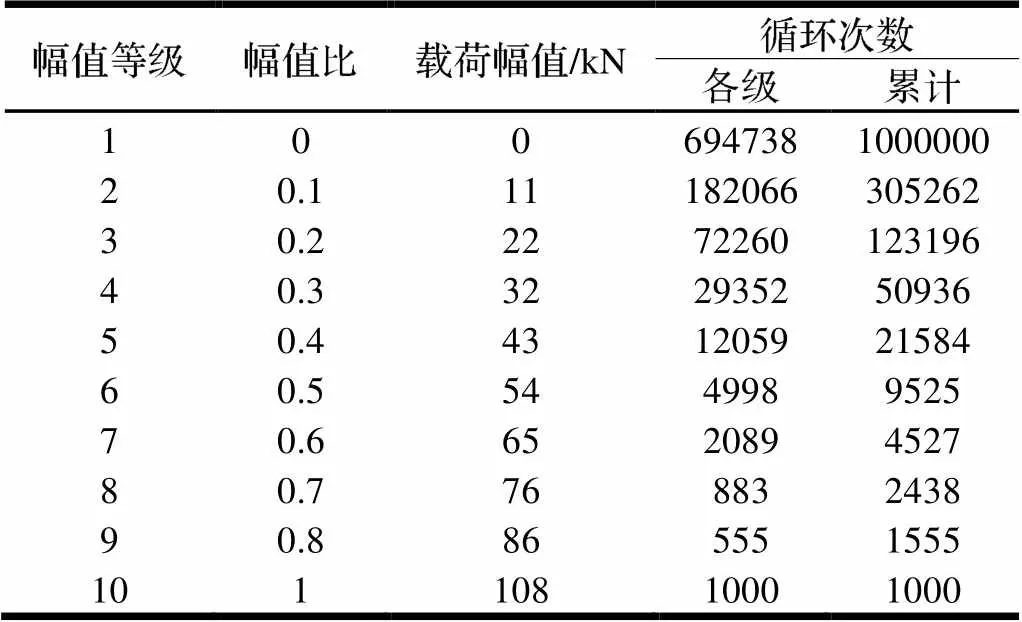
表8 Fz所有工况载荷幅值一维10级载荷谱
3.5 最终载荷谱的生成
得到载荷均值的总波动中心与幅值一维10级载荷谱后,将幅值的10级载荷叠加于载荷均值的总波动中心,即可获得最终的风电轴承试验载荷[11],载荷的作用时间通过表7中载荷作用次数除以轴承试验转速确定。根据疲劳损伤累积的特点,加载次序为小-大-小,一个循环结束后重复加载,直至轴承失效,加载方式如图5所示。
得到F的一维10级载荷谱后,用同样的方式可以获得其余F、F、M、M载荷的一维10级载荷谱。合并结果后得到该型轴承试验总载荷谱,如图6所示。其中因主轴承绕轴方向转动,所以M的大小对轴承强度不产生影响,本载荷谱不考虑M。
由最终载荷谱可看出,完成一个完整循环大约需1200 h,时间主要集中在前5级载荷上。
4 结论
针对风电主轴承载荷变化频率快、大小和方向均不规律等特点。本研究以某型号2.5 MW风电主轴承为例,通过从单一工况延展到多种工况、由一种载荷合并为全载荷,详细进行了风电主轴承试验台载荷谱的编制,该方法的核心是雨流计数法统计原始载荷,再利用威布尔三参数方程扩展已知数据,最终得到了该型风机主轴承在30种工况下的10级实验载荷谱。此方法既保留了载荷的原始特征,又极大地简便了实验加载难度,对风电轴承疲劳寿命实验提供了有效指导。
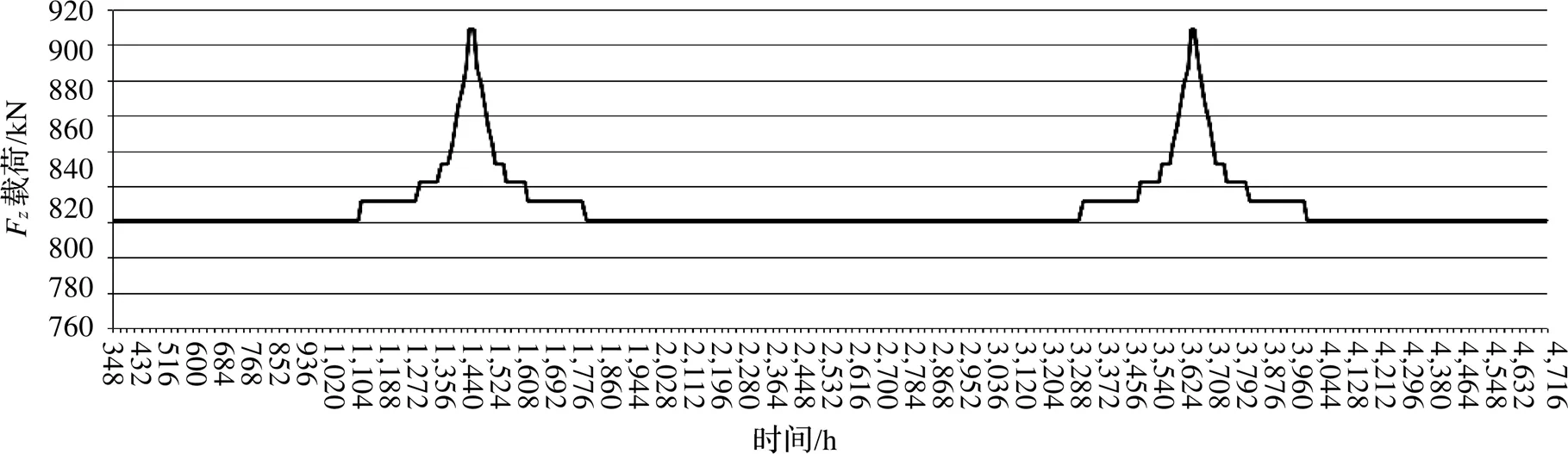
图5 Fz载荷谱加载方式(一维10级载荷谱)

图6 全载荷一维10级载荷谱(一维10级载荷谱)
[1]林勇刚. 大型风力变桨矩控制技术研究浙[D]. 杭州:浙江大学,2005.
[2]刘贝贝. 兆瓦级风电变桨偏航和主轴承试验机的研制[D]. 大连:大连理工大学,2013.
[3]高聪颖,王宇炎,李云峰,等. 风力发电机变桨轴承载荷谱的处理[J]. 轴承,2012,10(5):19-20.
[4]陈观慈,贾平,毛范海,等. 风电轴承多工况试验载荷谱的编制[J]. 轴承,2011(10):21-25.
[5]Adam Niestony. Determination of Fragments of Multiaxial Service Loading Strongly Influencing the Fatigue of Machine Components[J]. Mechanical Systems and Signal Processing,2009(23):2712 -2721.
[6]易当祥,李祥臣,田村祥,等. 导弹产品湿热载荷统计分析与载荷谱设计[J]. 强度与环境,2013(2):50-53.
[7]傅惠民,高镇同. 确定威布尔分布三参数的相关系数优化法[J].航空学报,1990,11(7):323-327.
[8]严晓东,马翔,郑荣跃,等. 三参数威布尔分布参数估计方法比较[J]. 宁波大学学报(理工版),2005(9):301-305.
[9]胡恩平,罗兴柏,刘国庆. 三参数Weibull分布几种常用的参数估计方法[J]. 沈阳工业学院学报,2000,19(3):88-94.
[10]邱宣怀. 机械设计[M]. 北京:高等教育出版社,2007:1-7.
[11]王建定,桑正中,陈翠英. 程序载荷谱编制方法研究[J]. 农业机械学报,1986(3):71-81.
Compilation of Load Spectrum of Large MW Wind Turbine Main Bearing under Multiple Working Conditions
DAI Lisi,HU Xingtao,XIAO Xia
(1.Sichuan Machinery Research & Design Institute (Group) Co., Ltd., Chengdu 610031, China;2.Sichuan Aerospace Fenghuo Servo Control Technology Corporation, Chengdu 611130, China)
When the main bearing of wind turbine is tested for fatigue life, the frequency of the original load data measured under the actual working condition changes too fast to be loaded directly on the test-bed. It is the basis of the whole fatigue test and the theoretical basis of fatigue life estimation to process the original load data effectively and make the bearing load spectrum which is convenient for the test-bed loading. This study takes a 2.5 MW wind turbine main bearing as an example to compile a new load spectrum of multi-condition full load bearing. From a single working condition to multiple working conditions, one load is combined into a full load. The core of the compiling method is to count the original load by rain-flow counting method first, and then extend the known data by using three-parameter Weibull distribution. Finally the 10-level experimental load spectrum of the main bearing under 30 working conditions is obstained. This load spectrum not only retains the basic characteristics of the original data, but also simplifies the loading mode, making the bearing test loading possible.
wind turbine main bearing;load spectrum;rain-fall counting method;Weibull distribution;multi-working load
TM315
A
10.3969/j.issn.1006-0316.2021.03.012
1006-0316 (2021) 03-0074-07
2020-05-22
戴莉斯(1987-),女,四川成都人,硕士,工程师,主要从事流体机械、工程机械方向的项目研发工作,E-mail:597716416@qq.com。
