2020年国际物理奥林匹克竞赛实验试题介绍及解答

2021-05-12穆良柱陈志坚陈晓林

物理实验 2021年4期

荀坤，李智，穆良柱，陈志坚，陈晓林

(北京大学物理学院，北京 100871)

因新冠肺炎疫情全球爆发，原计划于2020年7月在立陶宛共和国举行的第51届国际物理奥林匹克竞赛(IPhO)被顺延至次年. 就在各队为本年度选手失去参赛机会而惋惜时，俄罗斯在国际物理奥林匹克竞赛委员会的授权下主办了此次特别的国际物理奥林匹克竞赛(International Distributed Physics Olympiad, IdPhO2020)，各参赛方在主办方代表监督下在本国参加比赛. 经主办方艰苦努力和各参赛方密切配合，竞赛得以于2020年12月8—15日在跨越14个时区的全球多地成功举行. 2020年初选拔产生，9月已经进入北京大学学习的5名代表中国参赛的选手以较大优势包揽了本次竞赛的前5名. 其中，来自长沙市第一中学的张意飞同学更是赢得了理论、实验和总成绩3项第一.

竞赛实验器材由主办方代表在考试前2 h带到考场. 实验试题名为“晶体学”，时长为5 h，不要求分析误差[1]. 试题内容几乎涵盖了通过衍射确定晶体结构的所有方面，篇幅长，内容多，故介绍试题时会在图文上做一定压缩. 试题解答的重点也放在方法和最后结果上，中间过程能省则省略. 本文结构参考了文献[2].

1 试题介绍

晶体是指由1个基本单元(晶胞)在空间周期性排列形成的结构. 如ρ(r)为描述晶体结构的实函数，a1,a2和a3为3个线性无关的矢量，则对整个晶体有：

ρ(r+e·a1+f·a2+g·a3)=ρ(r),e,f,g∈Z,

(1)

其中，a1,a2和a3被称为晶格矢量，简称格矢. 晶体也可以只是一维或二维的. 本题的任务是确定晶体结构，也即晶胞结构ρ(r)和格矢a1,a2和a3.

图1 散射矢量示意图

要求：在A部分以衍射光栅(一维晶体)为例研究晶体衍射的最基本规律；在B,C和D部分要分别确定未知晶体的晶格参量、晶胞的对称性和结构细节.

1.1 从狭缝到晶体

如图2所示，衍射光栅是最简单的一维晶体，狭缝和两狭缝间的区域构成晶胞，格矢a1等于光栅常量a.

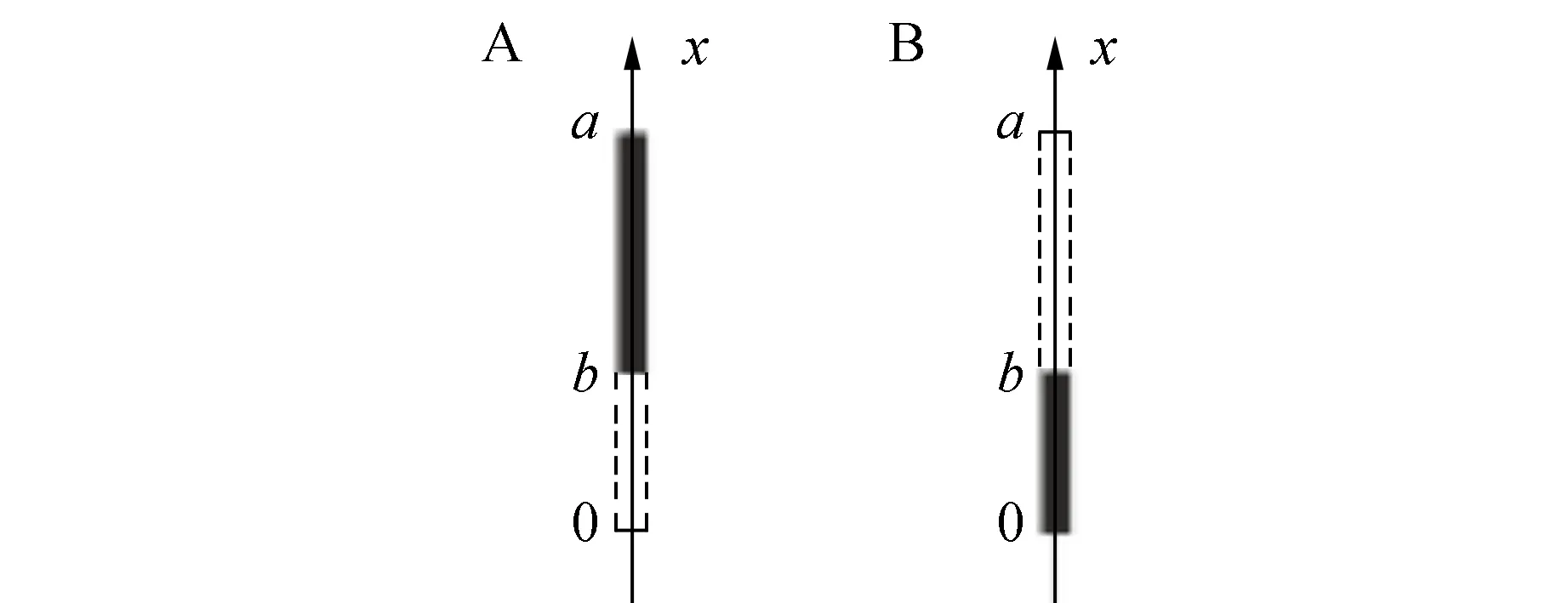
图2 一维晶体的晶胞(不透光区域用粗黑线表示)

当观察光栅的夫琅禾费衍射时，光强与衍射角θ的关系为

(2)

其中，I0为θ=0时的光强，N为被照明的光栅狭缝数.

A.1 利用散射矢量q(q≪ki)重新写式(2). (0.3分)

A.2 写出光栅常量为a的光栅的第h个衍射极大的散射矢量q. (0.2分)

A.3 设q1为1级衍射极大对应的散射矢量. 用q1表示各级衍射极大的散射矢量q.q1和a间有何关系？(0.2分)

A.4 观察样品DG1～DG5的衍射. 用实验方法确定每一样品的q1和a. 画出装置示意图，写出所测得的量及用于计算的公式. (1.0分)

A.5 由实验得到样品DG3～DG5的a与b之比a/b. 用公式和示意图来解释求解方法. 已知b≤a/2. (1.5分)

衍射极大的位置和强度分别由晶体的周期(a1=a)和晶胞参量(狭缝宽度b)决定. 为简化强度计算，可以引入被称为结构因子的复函数：

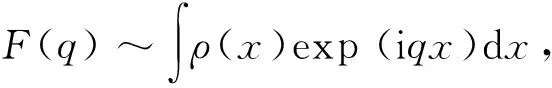
(3)

其中，ρ(x)是振幅透射率(本题中可视为实数)，q是散射矢量，积分区域为整个晶胞(本文所有结构因子表达式的积分区域也都是整个晶胞，一般不再标出). 将所对应的q代入，得到各衍射极大的相对强度：I=|F|2.

衍射强度极大位置(衍射斑点)总可以表示成矢量(倒格矢)之和：

1D：q=h·q1,

(4)

2D：q=h·q1+k·q2,

(5)

3D：q=h·q1+k·q2+l·q3,

(6)

其中h,k,l∈Z.

每个衍射斑点，以3D的为例，可以用1组数(h,k,l)标记，对应的复振幅和强度分别记为F(h,k,l)和I(h,k,l).

A.6 按图2坐标系写出图2中A所示衍射光栅晶胞的ρ(x). 设光栅常量a=pb,p∈N，计算此晶胞由h标记的衍射斑点的结构因子FA(h)，用h和q1表示. 哪些极大的强度为0？写出这类极大的h满足的方程. (0.7分)

A.7 对另一个晶胞(图2中B)重复A.6. (0.7分)

1.2 2D晶体

图3为以a1和a2为格矢的2D晶体，习惯上取格矢间夹角α≤90°，图中圆点表示晶体中的等价位置. 如果平行单色光垂直照射到如图3所示的2D晶体面上，会在其后的屏上出现周期性的衍射花样，各极大位置可以用式(5)描述.

图3 2D晶体

B.1 用晶体参量a1,a2和α(图3)表示矢量q1和q2的长度及其夹角β. (1.0分)

图4给出了4种晶胞都为正方形的晶体，2个格矢长度相等且相互垂直. 晶胞内黑色正方形完全不透光，其他部分则完全透光. 对晶胞C有b′>b. 晶胞D中2个黑方块完全相同，一个相对于另一个向右和向上分别移动了半个格矢.

图4 A～D的晶胞是正方形(除aB>aA外，其他尺寸比都未知)

B.2 对晶体A和D给出衍射斑点(h,k)对应的结构因子的模|F(h,k)|，用a和b表示. 只需给出1个除中心斑点(h=0,k=0)外都成立的表达式. (1.0分)

B.3 观察样品UC1～UC4的衍射花样，用实验方法确定它们的晶体周期aUC1,aUC2,aUC3和aUC4. (0.6分)

B.4 给出UC1～UC4与图4中各晶胞的对应关系，并做解释. (0.4分)

B.5 确定尺寸b. (0.8分)

B.6 样品UC5～UC7是简单的2D晶体.

观察它们的衍射花样，用实验方法确定每一样品的参量a1,a2及其夹角α，并解释用到了衍射花样的哪些参量. (1.2分)

1.3 晶体的对称性

如图5所示，实际晶体的晶胞中常常会含有存在对称性的几个分子. 知道这些对称性有助于确定晶胞结构. 晶胞的对称性会使得h和k满足某些条件的衍射斑点系统性缺失(消光).

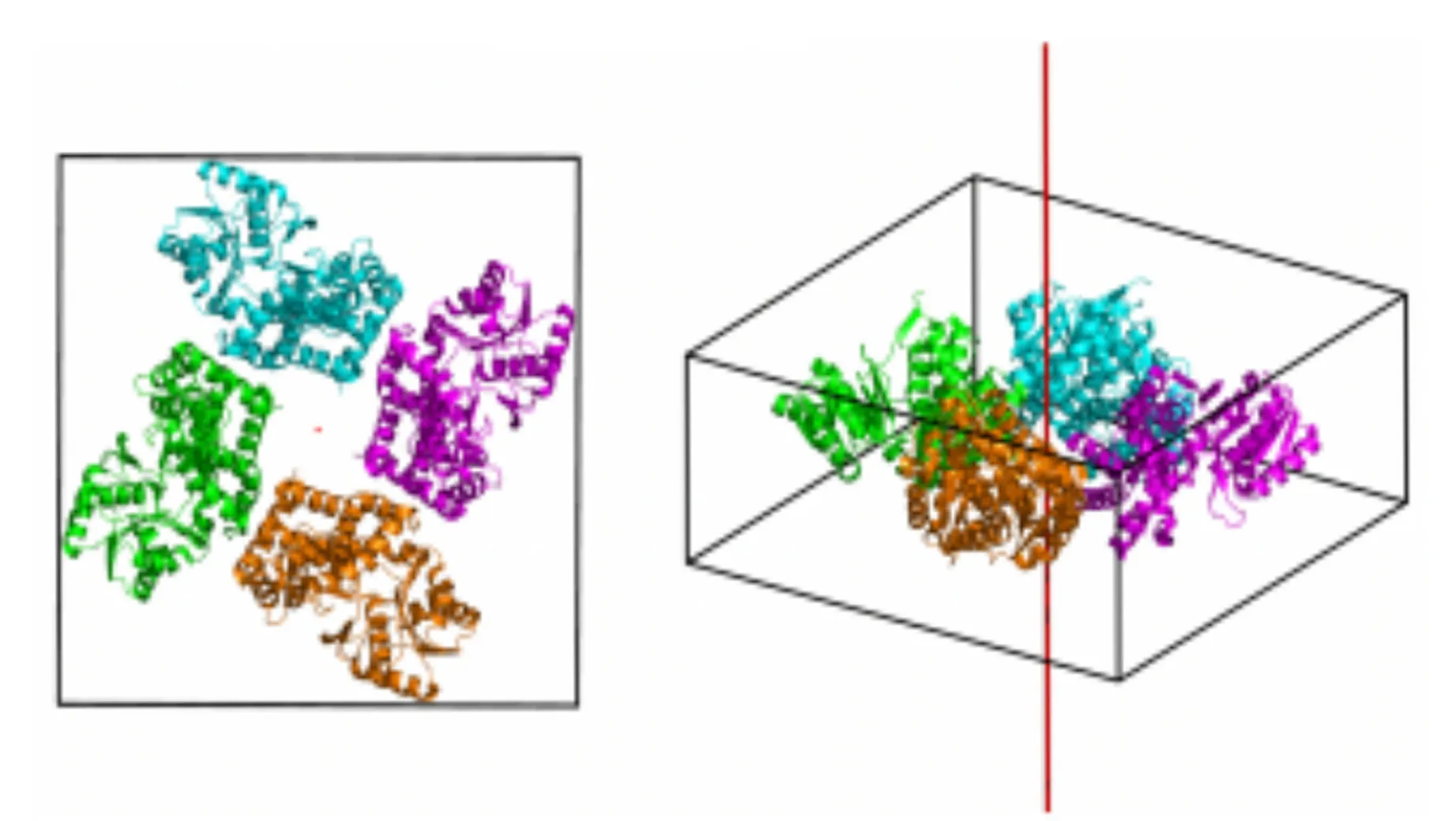
(a) (b)图5 晶胞具有C4对称的示例[绕图(b)中竖直线转90°的整数倍后晶胞会复原]

图6是格矢大小相等(a1=a2)且相互垂直的2D晶体的衍射图(仅画了|h|,|k|≤2的部分).

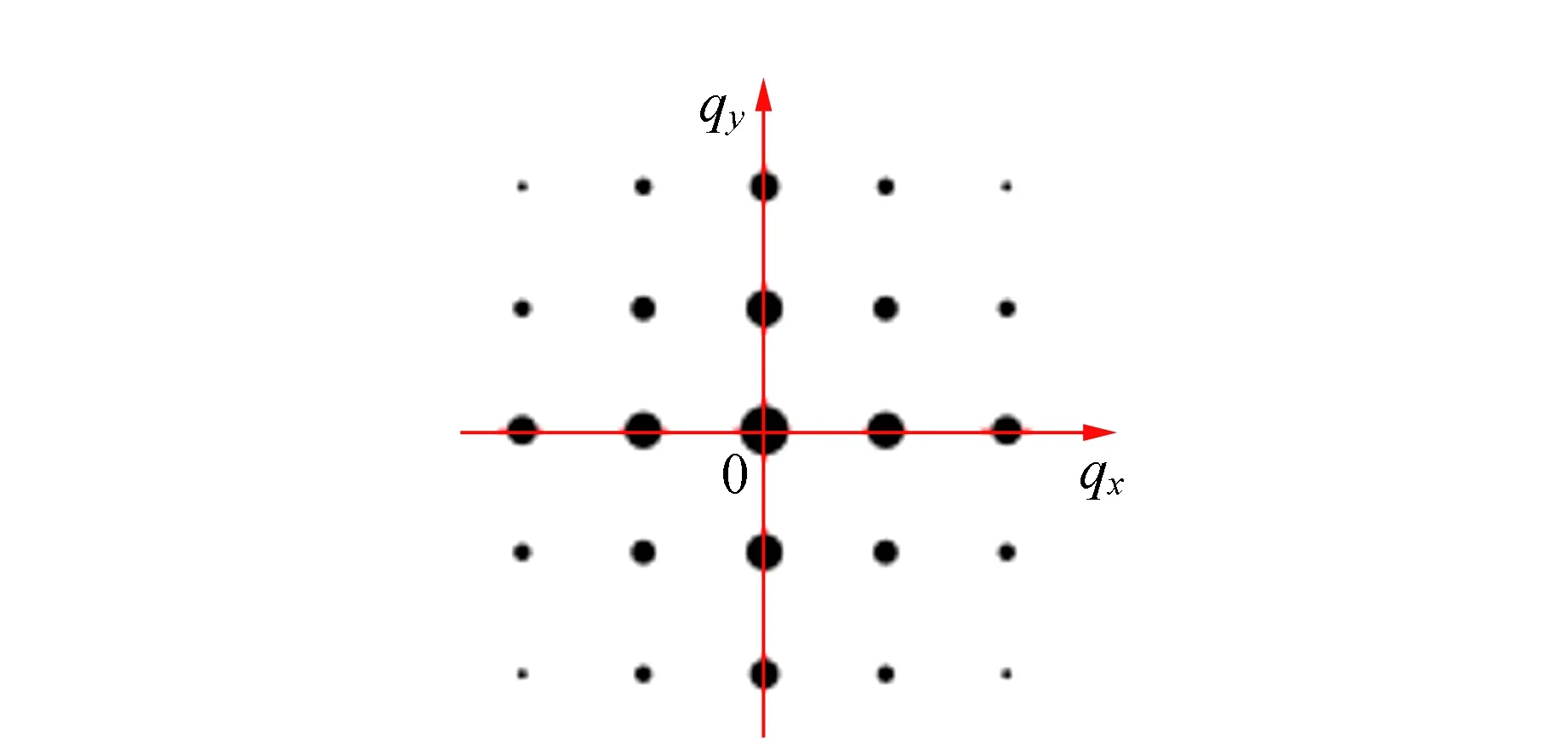
图6 2D晶体的衍射图

C.1 给出其旋转对称中心的h和k. 该图的旋转对称阶m可能取哪些值？画出所有可能的镜像对称轴，并给它们命名. (0.3分)

C.2 写出上一任务中你所画出并命名的每一镜像对称轴的直线方程. (0.2分)

C.3 对每一旋转对称和镜像对称，写下它们的记号(旋转对称用Cm，镜像对称用直线方程)，以及存在该对称元素时强度I(qx,qy)满足的方程. (0.4分)

C.4 写出衍射斑点(h,k)和(-h,-k)的强度满足的方程. 指出任务C.1中与此方程相对应的对称性并做解释. (0.2分)

图7各晶胞中的白、黑格子分别代表透光和不透光. 晶胞2和3分别由晶胞1对x=0轴和x=y做镜像变换得到. 晶体4由晶体1平移(x1,y1)得到.

(a)1：原初 (b)2：x=0 (c)3:y=x (d)4:平移图7 通过不同对称操作可由晶体1得到晶体2～4

C.5 利用结构因子的定义和对称性，分别将晶体2～4的结构因子用晶体1的结构因子表示. (0.4分)

C.6 2D晶体中旋转对称阶m只能取哪些值？说明原因. (0.5分)

参照答题纸上所给晶胞示意图18：

C.7 确定晶胞K，L，M，N，P，Q，R，S和T具有的对称性，镜像对称轴直接画在图中，旋转对称符号标在图下方. (0.9分)

C.8 观察样品PG1，2，5和8的衍射花样，确定这些衍射花样有何对称性，并给出它们与晶胞K，L，M和N间的对应关系. (0.8分)

C.9 观察样品PG3，4，6，7和9的衍射花样，给出它们和晶胞P，Q，R，S和T间的对应关系，并说明理由. (1.0分)

C.10 观察样品UC8的衍射花样. 它可能是晶体吗？请解释原因. (0.3分)

1.4 相位问题

入射光经晶体散射后的复振幅由下式(傅氏变换)给出：

(7)

由结构因子经逆傅氏变换亦可反推出：

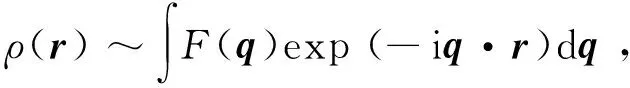
(8)

对离散衍射斑点，积分可以变成求和：

ρ(r)～∑|F(q)|exp (iφ)·exp (-iq·r).

(9)

实际只需对式(9)中的强衍射斑点求和即可. 衍射斑点强度能给出结构因子的模，但不能给出相位，由式(9)不能直接解出ρ(r). 为此，通常会取近似的初始相位，先用式(9)得到ρ(r)，再将得到的ρ(r)代入式(7)来更新相位，不断重复，直到收敛. 如果已知某晶体结构与待测晶体的类似，即可用该晶体的相位作为待测晶体的初始相位.

MR0，MR1和MR2的晶胞都由4×4阶的透光(ρ=1)或不透光(ρ=0)方块组成. MR0的晶胞结构已知，如图8所示.

图8 MR0的晶胞结构(白方块透光，黑方块不透光)

晶体MR1结构未知，但应为图9中之一. 晶体MR2的结构和MR0的非常接近，但有7个透光方块. 图10给出了MR0晶体|h|,|k|≤2衍射斑点的相位(单位为rad).

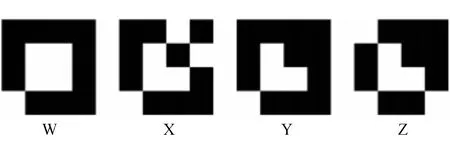
图9 MR1晶体可能的晶胞

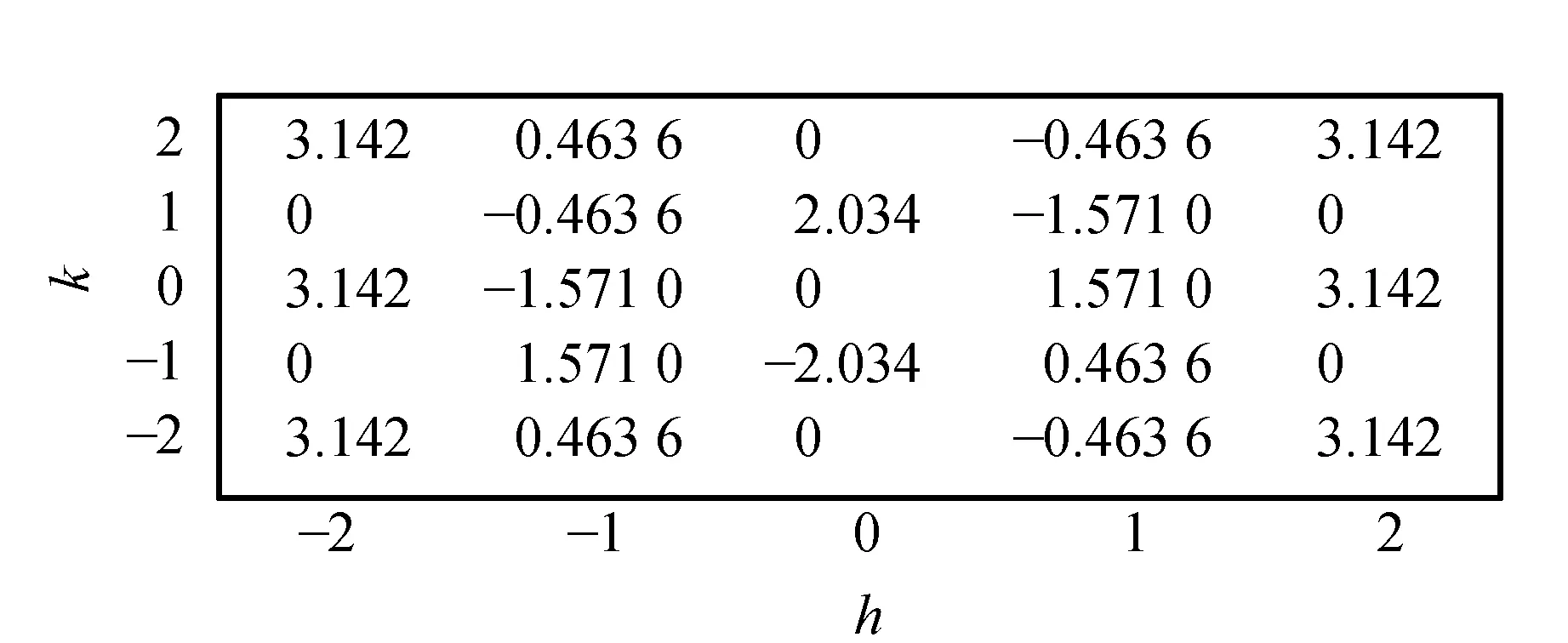
图10 MR0晶体|h|,|k|≤2衍射斑点的相位

D.1 如果入射光强为I0，请给出MR0或者MR2的0级衍射斑点的强度. (1.0分)

D.2 确定晶体MR1的晶胞，并说明原因. (2.0分)

D.3 若MR2的晶胞与MR0的差别仅为其中2个方格从不透光变成透光，请确定其结构. (2.0分)

1.5 实验器材

实验器材如图11所示. 1为数字万用表，2为带磁铁的光电二极管，3为9 V电池，4为10 kΩ和200 kΩ电阻，5为连接器(4个)，6为电池引线座，7为630 nm波长激光器，8为光具座，9为针，10为胶带，11为螺丝刀，12为直尺，13为大铁夹(2个)，14为卷尺，15为样品(分别标有Diffraction grating, Unit cell, Plane group和Molecular replacement)，16为衰减片，17为小铁夹(4个)，18为样品座(需自己组装)，19为绘图纸，20为黑卡纸，21为带磁性的平板.

图11 实验器材(白线画出的左上部用于光强测量)

图12示意了如何将激光器装在光具座上并且用大铁夹来控制其开关，如何用针和胶带纸减小激光光束的尺寸，以及如何用衰减片来减弱光强. 图13示意了激光器、样品和观察屏应该如何放置.

图12 激光器和衰减片的使用示意图

图13 激光器、样品和观察屏的放置示意图

流过光电二极管的电流与照在其上的光强成正比. 用电池引线座和连接器将万用表、光电二极管、电阻和电池按图14连接，就可得到光强探测器. 电阻大小可视光强做选择.

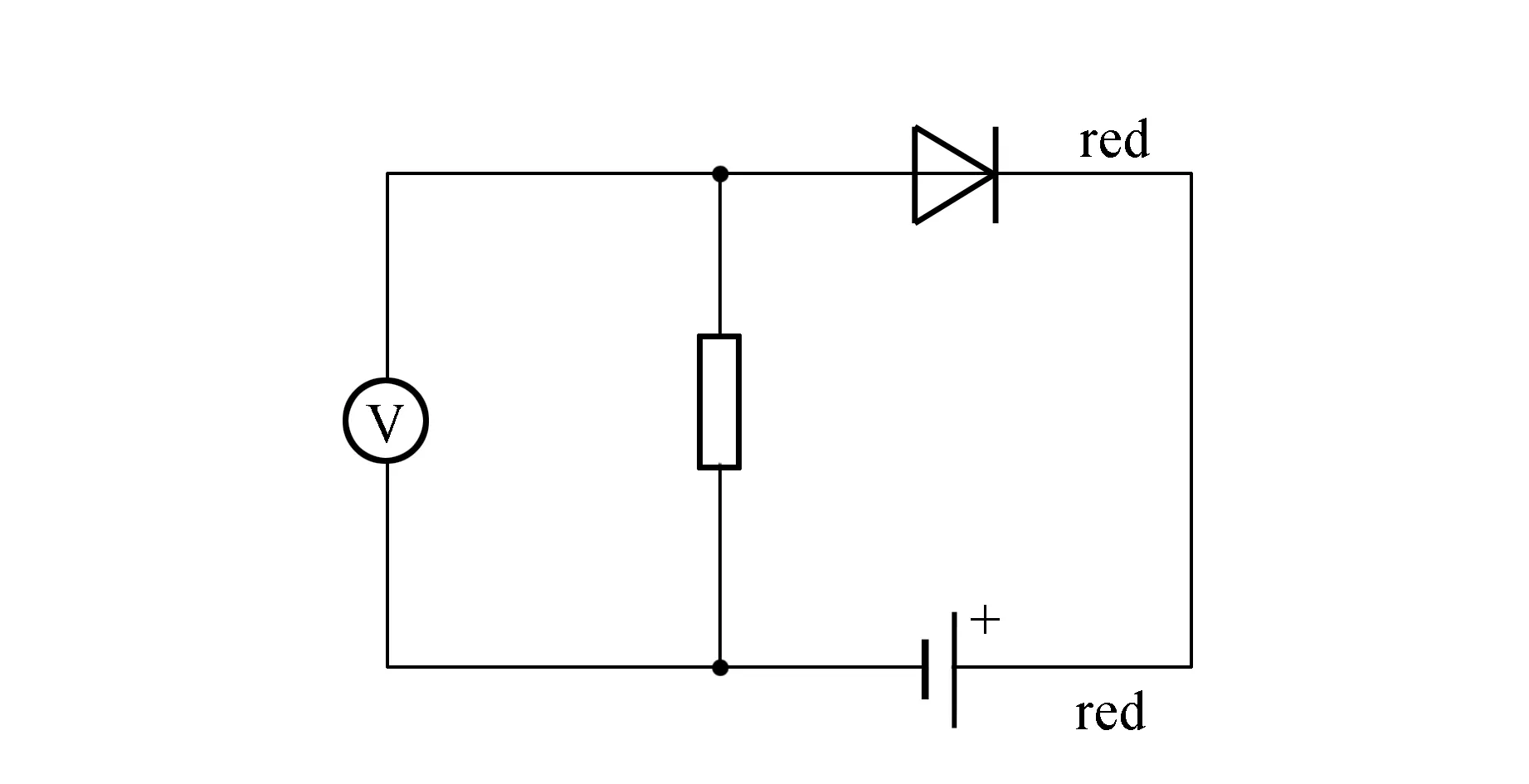
图14 光强探测器线路

2 试题解答

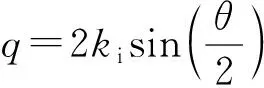
(10)

A.2 可由光栅衍射方程直接推出：

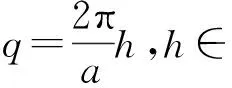
(11)

A.3 由式(11)立即可得：

q=q1h,h∈Z,

(12)

q1a=2π.

(13)

A.4 图15为衍射光路示意图，其中，L和sN分别是样品到观察屏和0级到第N级衍射斑点的距离.

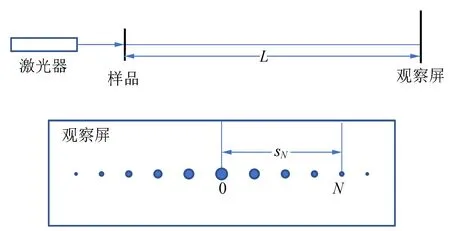
图15 衍射光路及衍射光斑示意图

确定q1的公式为

(14)

q1与a满足：

q1a=2π.

(15)

对每一样品，分别测量L和sN，再利用式(14)和(15)，求出对应的光栅常量. 标准答案为

DG1:q1=(320±32) mm-1,a=(20±2) μm;

DG2:q1=(130±13) mm-1,a=(50±5) μm;

DG3～DG5:q1=(79±8) mm-1,a=(80±8) μm.

A.5 由式(10)推出第h级衍射极大的强度为

(16)

则第1和第2级衍射极大强度满足：

(17)

将测得的第1和第2级衍射极大强度值代入，可解出a/b. 标准答案为

DG3:a/b∈[7，10];

DG4:a/b∈[3.2，4.8];

DG5:a/b∈[1.5，2.5].

式(17)是超越方程，规则不允许使用可编程计算器，很难求解. 中国选手普遍采用某级衍射极大缺失来求a/b，被以方法没有普适性为由扣分. 实际上也观察不到衍射斑点明显缺失. 其实，利用0级衍射光强和透光面积平方成正比就可以快捷地求出a/b. 更简单地，将光电二极管紧贴在光栅之后测量光栅平均的透光率也可以求出a/b. 用这2种方法得到的DG3，DG4和DG5的a/b分别为：7.9和7，3.4和4，2.1和2，均落在标准答案区间内.

A.6 对照图2直接可以写出：

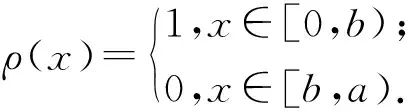
(18)

将式(18)代入式(3)，经积分、化简后可得：

(19)

其中，p=a/b. 强度为0的极大点满足：h=±pm,m∈N.

A.7 仿照A.6，不难得到：

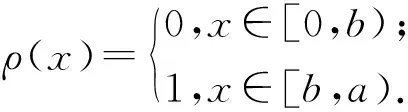
(20)

(21)

强度为0的极大点满足：h=±pm,m∈N.

可以看出图2中A和B的非0级衍射斑点强度完全相同.

A.8 对比式(19)和(21)，立即可得：

B.1 总可以在图3中画一系列过格点的平行线使所有格点落在这些平行线上. 这样，在垂直于这些平行线的方向上，1个2D晶格的衍射可以看成光栅常量为平行线间距的光栅的衍射.q1和q2标示的是距0级斑点最近的衍射斑点，对应平行线间距最大时的衍射. 平行线间距最大意味着平行线上相邻2点的距离最短. 也就是说这样的平行线方向只能与a1或a2一致. 不难导出，对应的线间距分别为a2sinα和a1sinα.

从上面讨论可以看出，q1和q2分别与a1或a2之一垂直，不妨取q1⊥a2，有：

(22)

q1和q2的夹角β=α.

B.2 标准答案只给了晶体A的结构因子. 由式(19)和式(21)可以看出，如果透射率0与1互换，非0级衍射斑点结构因子的模相同. 因此，可以用透光与不透光区域正好相反的结构来代替晶体A：

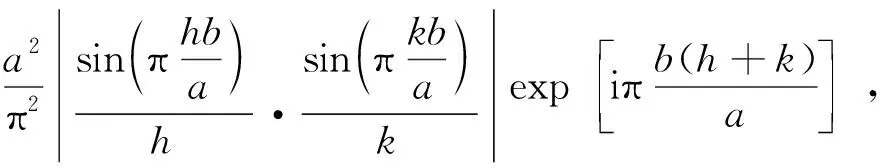
(23)

或

h≠0,k≠0.

容易推出，晶体D的结构因子为晶体A的结构因子乘以因子[1+eiπ(h+k)].

B.3 采用和A.4相同的光路，在衍射屏上会看到类似图6的衍射图. 测量斑点间距即求出衍射矢量，再由衍射矢量求出晶体周期. 标准答案为：aUC1=(29.5±2.0) μm,aUC2=(19.7±1.3) μm,aUC3=(19.7±1.3) μm或者aUC3=(13.9±1.0) μm,aUC4=(29.5±2.0) μm,其中UC3有2种答案：一种对应晶胞D，另一种改变晶胞取法使其内只包括1个黑方块.

B.4 观察各样品的衍射花样：

1)由h+k为奇数的斑点缺失，可以断定UC3对应晶体D.

2)由aB>aA，结合B.3的结果知UC2对应晶体A.

3)由UC1的0级斑点强度明显比UC4的强，知UC1对应晶体B，UC4对应晶体C.

B.5 标准答案说，比照A.5中的方法，用UC1的实验结果可以得到b=(10±2) μm. 其实也可以通过比较A和B 2种晶体的0级斑点强度来测量，这样测得的结果为b=9.6 μm.

B.6 观察各样品的衍射花样：

1)UC5的衍射斑点为矩形排布，仿照B.3求得：a1=(19.7±1.8) μm,a2=(39.4±3.5) μm.

2)UC6和UC7的衍射斑点均呈平行四边形排布. 测量平行四边形的2条边长，依式(22)计算出q1和q2模的大小. 测量平行四边形内锐角，即得q1和q2间夹角β.

标准答案：UC6的a1=(35.5±3.2) μm，a2=(22.1±2.0) μm,α=(63±6)°；UC7的a1=(39.4±3.5) μm,a2=(35.4±3.2) μm，α=(56±6)°.

C.1 旋转对称中心为h=0,k=0，旋转对称阶m=1,2,4. 图16中用1～4标出的4条直线是镜像对称轴.

图16 标注了镜像对称轴的衍射图

C.2 图16中各镜像对称轴满足的方程：1为qy=0,2为qy=qx,3为qx=0,4为qy=-qx.

C.3 某种对称元素存在时，强度I(qx,qy)满足的方程如下：

C1:I(qx,qy)=I(qx,qy),

C2:I(qx,qy)=I(-qx,-qy),

C4:I(qx,qy)=I(-qy,qx),

qy=0:I(qx,qy)=I(qx,-qy),

qx=0:I(qx,qy)=I(-qx,qy),

qx=qy:I(qx,qy)=I(qy,qx),

qx=-qy:I(qx,qy)=I(-qy,-qx).

C.4 由于本题中ρ(x)可视为实数，结构因子存在如下关系：

(24)

由此可以推出：

I(-h,-k)=I(h,k),

(25)

与此相应的对称性为C2.

C.5 设晶体1的结构因子为

晶体2可以由晶体1对x=0轴做镜像变换得到，其结构因子满足：

F(-qx,qy).

晶体3 可以由晶体1对y=x轴做镜像变换得到，其结构因子满足：

F(qy,qx).

晶体4可以通过晶体1做平移得到，设平移矢量为(x1,y1)，其结构因子满足：

exp [i(qxx1+qyy1)]=

F(qx,qy)exp [i(qxx1+qyy1)].

C.6 如图17所示，A和B是晶体中的2个格点(完全等价). 如绕A点逆时针旋转角度θ，则B点变化到C点. 若此为晶体的对称操作，则晶体还和原来一样. 这时再将晶体绕A点顺时针旋转角度θ，晶体会回到未做任何操作前的状态. 即，如逆时针旋转θ角是对称操作，则顺时针旋转θ角也必定是. 又因所有格点等价，对A点成立的对B点也必定成立. 故，如图17所示，C和D必为晶体格点.CD显然平行于AB. 由晶体的平移对称性可以断定CD的长度一定是周期a的整数倍. 也即：

(26)

图17 能使晶体复原的转角

C.7 各晶胞的镜像对称轴和旋转对称符号分别直接标在图18对应的结构图内和图下.

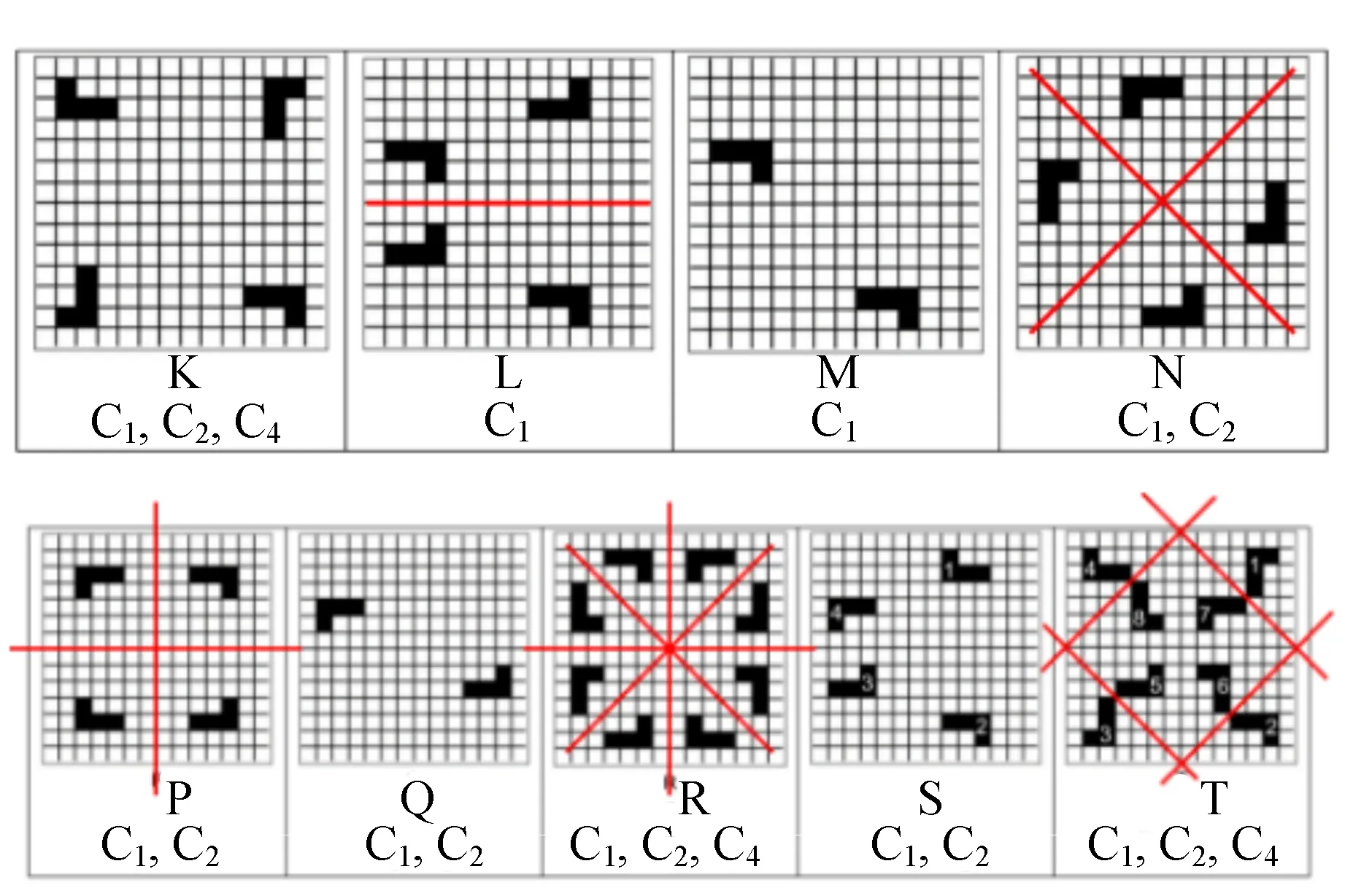
图18 晶胞的对称性

C.8 标准答案给出PG1，2，5和8的衍射花样的对称性见表1，“+”表示存在相应的对称性. PG1的qx=0镜像轴理论上也应该存在，但不一定能够观察到.

表1 PG1，2，5和8衍射花样的对称性

由存在明显的qy=0镜像轴，推出PG1对应L. 由4种镜像轴和C4均不存在，可推出PG2对应M. 由存在qx=qy和qx=-qy对称轴，推出PG5对应N. 由存在C4对称推出PG8对应K.

C.9 标准答案给出的PG3，4，6，7和9衍射花样的对称性见表2.

表2 PG3，4，6，7和9衍射花样的对称性

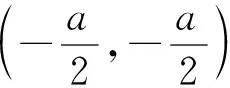
f1+5(h,k)=F(h,k)+F(k,h)e-i(h+k)π,

f4+6(h,k)=F(-k,h)+F(h,-k)e-i(h-k)π,

f3+7(h,k)=F(-h,-k)+F(-k,-h)ei(h+k)π,

f2+8(h,k)=F(k,-h)+F(-h,k)ei(h-k)π.

晶胞T的结构因子为上面4项之和. 对h=0的衍射斑点有：

fT(0,k)=[F(0,k)+F(k,0)+F(0,-k)+

F(-k,0)](1+eikπ),

也即当h=0时，k为奇数的斑点会缺失. 显然，当k=0时，h为奇数的斑点也会缺失. 由PG6衍射花样具有这样的特性，可以确定其与T对应. 而PG4不具有这样特性就只能与R对应.

S晶胞的不透光“L”型单元2，3和4可以由1经过旋转或镜像加平移得到. 比照C.5的解答可以得到如下关系：

f1(h,k)=F(h,k),

f2(h,k)=F(-h,-k)ei5πh/7,

f3(h,k)=F(-h,k)e-iπ(2h/7+k),

f4(h,k)=F(h,-k)e-iπ(h+k).

对于h=0的衍射斑点，S晶胞的结构因子为

FS(0,k)=[(F(0,k)+F(0,-k)](1+e-ikπ)，

即，h=0的衍射斑点在k为奇数时会缺失. 类似地也可以推出：k=0的衍射斑点在h为奇数时会缺失. 衍射花样具有这样特性的，除PG6外，就只有PG9，所以它对应S. 这里需要指出：在对qx=0轴做镜像变换后，再向上平移半个周期，S晶胞依然能复原，所以PG9的衍射花样也存在qx=0和qy=0的镜像对称.

PG3有镜像对称轴，而PG7没有，故前者对应P，后者对应Q.

C.10 实验观察到UC8的衍射花样具有C10旋转对称. 根据C.6的证明，它不可能是晶体. 实际上UC8是准晶，具有C5对称.

D.1 0级斑点的光场强正比于透光面积，而光强则为场强的平方. MR0和MR2的总面积均为16个方块，透光面积分别为5和7个方块. 16个方块都透光时光源与屏间无任何遮挡，0级光强就是入射光强，故：

D.2 标准答案所给MR1各衍射斑点强度见图19.

图19 MR1各衍射斑点的强度

考虑到透射率为实数，逆傅氏变换可写成：

(27)

其中，(χ,γ)是构成晶胞方格的坐标. 将图19中斑点光强和图10中MR0晶胞对应斑点相位φ用于式(27)，可得到图20. 据此，可以判断MR1的晶胞应为图9中X.

图20 MR1晶胞的振幅透射率

标准答案采用的逆傅氏变换方法工作量极大，也不绝对可靠. 其实可以有更快捷的方法. MR0,MR1和MR2是并排印在同一胶片上的，肉眼即可分辨出MR1的透光率介于MR0和MR2之间. 由MR0和MR2的透光方格数分别为5和7，可推出MR1的透光方格数为6，只可能是图9中X或Z.

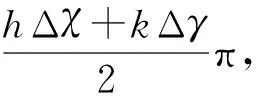
D.3 标准答案所给MR2各衍射斑点的强度见图21. 按照D.2方法可得MR2各方格的试探透射率如图22所示.

图22 MR2晶胞的透射率

比较图22与MR0晶胞结构，只有(0,3)和(2,0)方格变成透光. 因此，推测MR2具有形如图23的晶胞结构.

图23 MR2晶胞结构

也可以利用在D.2建议过的方法来确定MR2的结构. 对(0,2)衍射斑点，同行方格结构因子的相位相同，相邻行方格结构因子的相位相反. MR0只要第1行(从上往下)或第3行再增加1个透明方格，则6个透明方格的结构因子为0，第7个透明方格无论在什么位置都得不到强衍射斑. 所以，可以排除新增的2个透明格子出现在第1和第3行的可能. 在图24中，直接将这些格子涂黑,并用白底表示已知透明的方格.

MR0的5个透明方格的(1,1)衍射斑点结构因子两两抵消，只余下1个坐标为(1,2)[或(2,1)]的. 新增的2个透明方格中任何一个的相位都不能与其相反，否则得不到强斑(1,1). 由此可排除图24中X.

如新增的透明方格之一为Y，则(-1,1)衍射斑点必不弱，故图24中Y也不可能透明. 新增加的透明方格只有OP，OQ和PQ 3种可能. 由于各方格间只有同相、正交和反相3种关系，估计1个衍射斑点强度只需数秒时间. MR2衍射花样的1个明显特征是(1,-2)斑点强度明显强于(0,-2)的，只有OQ组合才与此相符.