非正态分布的三维连续体结构可靠性拓扑优化研究

罗 帅 苏 睿

(绍兴文理学院 土木工程学院,浙江 绍兴 312000)

0 引言

随着科学技术不断地进步,工程建筑也趋于复杂.在设计这类复杂工程建筑时,需要综合考虑如何提高结构的力学性能、提升材料的利用效率以及降低工程中的各类成本等.因此,优化设计便在设计领域占据重要的地位.目前优化设计主要有三种优化层次[1]:尺寸优化、形状优化与拓扑优化,三种优化形式又对应三个不同的设计阶段.尺寸优化与形状优化在面对大型复杂结构时,有设计周期长,优化效果不明显等缺点,因此难以保证在限定的时间里得到满意的设计结果[2].拓扑优化是最近几十年快速发展的一种新型结构优化方法[3].作为一种概念性优化方法,其优点是设计思路灵活,设计空间广阔.按结构类型可分为离散体结构的拓扑优化和连续体结构的拓扑优化[4].随着科研工作者的深入研究,均匀化法[5]、变密度法[6]、水平集法[7]、进化结构优化法[8]等方法相继被提出.

在传统的拓扑优化方法中,类似于尺寸、荷载等需要优化的参数一般设计为固定值,而且建立的优化模型一般是二维模型.但在实际工程中,这类参数可能是属于非正态分布的随机变量,需要优化的模型一般是三维空间模型.本文基于非正态分布的三维连续体结构拓扑优化研究,是将结构可靠性理论引入三维结构的拓扑优化中[9].将结构的可靠度作为优化模型的一个约束条件,得到同时满足结构可靠性和结构性能最优的拓扑优化结果[10].该方法不但可以有效地提高相关人员的工作效率,还可以减少各类生产成本,因此应用愈来愈广,也成为越来越多学者的主要研究内容.Kharmanda将可靠性理论引入拓扑优化设计中[11],提出一种可以使优化结构满足可靠度要求的拓扑优化方法(Reliability-Based Topology Optimization,简称RBTO).Meysam Johari[12]使用一阶和二阶可靠性分析对桥梁结构进行可靠度优化,探究结构柔度与不确定参数数量的关系. Aditya[13]等将随机矩阵理论(RMT)与RBTO结合,量化了不确定性并极大地提高可靠度计算的效率.Suwin提出一种基于模糊集方法对多目标可靠度的结构拓扑优化方法,满足结构的质量与强度设计要求[14].

本文选择将优化模型的几何尺寸和荷载作为非正态分布的随机变量,应用当量正态化法 (又称JC法,实际为当量正态化条件下的验算点法)[15],首先将非正态分布的随机变量转化成正态分布的随机变量,再根据当量正态化条件,得到当量正态化变量的均值和标准差,进而得到优化后的几何尺寸以及荷载[16].在此基础上, 基于变密度法,结合有限元分析,建立八节点六面体单元连续体结构优化模型.使用SIMP法[17]对优化模型进行插值处理,再以结构体积作为约束条件且以柔度最小化为目标进行拓扑优化工作,并展现优化成果.这种优化方法将可靠度优化与拓扑优化分开进行计算,两个部分单独进行循环,这可以有效增加计算效率,避免了两种优化的耦合影响计算速度.通过三维模型结构的算例证明该方法比传统拓扑优化方法优化效果更好,结构更轻,更具有实际工程意义.

1 可靠度分析

1.1 基本概念

传统的设计方案是设计人员结合自身的设计经验确定设计参数及区间,再按需要不断调整设计方案,直到其各类参数均满足设计要求.这就导致在变量复杂时,例如在结构几何尺寸和荷载的大小可变的情况下,优化结构的可靠性可能不符合预期,影响优化质量.当设计参数含有非正态分布随机变量时,如何使结构的拓扑优化结果有足够的可靠度就是当前设计人员主要研究的问题.在RBTO模型里,将变量的类型分成了三种：一是设计变量X,它是固定值;二是随机变量Y,它用来表示一些由概率分布的不确定变量；三是标准变量u,用来连接设计变量和随机变量.

在可靠度分析中,由设计变量X和随机变量Y表示的功能函数(或失效函数)为[10]：

Z=G(X,Y)

(1)

如图1所示,当Z>0时,结构为安全状态,当Z<0时,结构为失效状态,当Z=0时,结构处于极限状态.

结构无法达到预期设计性能的概率称为失效概率,用Pf表示,由失效概率的实际意义可知：

(2)

其中Pr(·)表示概率,fz(z)为概率密度函数.

图1 功能函数Z及可靠指标的几何意义

设随机变量Y=(Y1,Y2,…，Yn)T,n为随机变量的个数,那么联合概率密度函数为fY(y)=fY(y1,y2,…,yn),则结构的失效概率为：

(3)

但实际工程中,随机变量Y可能不是服从正态分布的,且联合概率密度函数也很难求解,直接计算多重积分更是繁琐复杂.因此引入可靠性指标β(如图1所示),β是一个无量纲数,失效概率可以表示为[18]：

Pf=Φ(-β)=1-Φ

(4)

通过式(4)便可快速得到满足工程精度要求的失效概率的近似值.

1.2 可靠度的一次二阶矩方法

为了得到可靠指标β的近似结果,可以将非线性功能函数Z按Taylor级数展开并取一次项,这就有一次二阶矩(FORM)法,在有非正态分布的随机变量时,可以通过当量正态化法将其转化为正态分布的随机变量,再利用验算点法便可得到可靠性指标β.

如图1所示,β的几何意义就是在标准空间内,从原点到极限状态面的最短距离.则求解β便可转化成用标准变量u求解以下最优化问题：

(5)

式(5)中,βt为给定的可靠度.

(6)

(7)

对式(6)求反函数得:

(8)

由式(7)解得:

(9)

由式(8)和式(9)便可得变量在当量正态化后的均值与标准差.

2 优化设计

2.1 变密度法

变密度法是一种常用的连续体拓扑优化建模方法,它实际上是在均匀化方法的基础上改进而来.变密度法的核心思想是让其材料单元的相对密度在闭区间[0,1]内变化,单元密度为0时优化为可以删除的孔洞单元,单元密度为1时优化为必须保留的实体单元[19].但这就会存在相对密度在开区间(0,1)内的单元,这样的单元很难直接判断是保留还是删除,因此Sigmund等提出了一种插值函数模型—固体各向同性材料惩罚模型(Solid Isotropic Microstructures with Penalization, SIMP)[20]用以减少在优化过程中出现的中间密度单元.

在SIMP模型中,经过插值函数优化的数学模型可以表示为：

(10)

式中,E(x)为经过插值函数优化后的材料的弹性模量,Emin近似表示为空白的单元的弹性模量,ρx代表第x个单元的相对密度,ρ为惩罚因子,ΔE=E0-Emin为相对密度表现为“1”的实体单元与相对密度表现为“0”的孔洞单元的弹性模量的差,通常取Emin=E/1000.

进而可得SIMP模型的刚度矩阵、柔度函数和灵敏度函数为[21]：

(11)

(12)

(13)

式(11)-式(13)中,K(ρ)为整体刚度矩阵,Kx表示第x个单元刚度矩阵除以其弹性模量得到的“单元”刚度阵.U为结构的位移向量,ρ表示设计变量,N为单元数目,C为结构的柔度,C′为灵敏度.

2.2 优化模型建立

2.2.1 拓扑优化数学模型

基于变密度法,以三维连续体结构的体积作为约束,以结构柔度最小化为目标的拓扑优化模型描述如下[22]：

Find:X={x1,x2,x3,…,xn}T∈Ω

(14)

F=KU

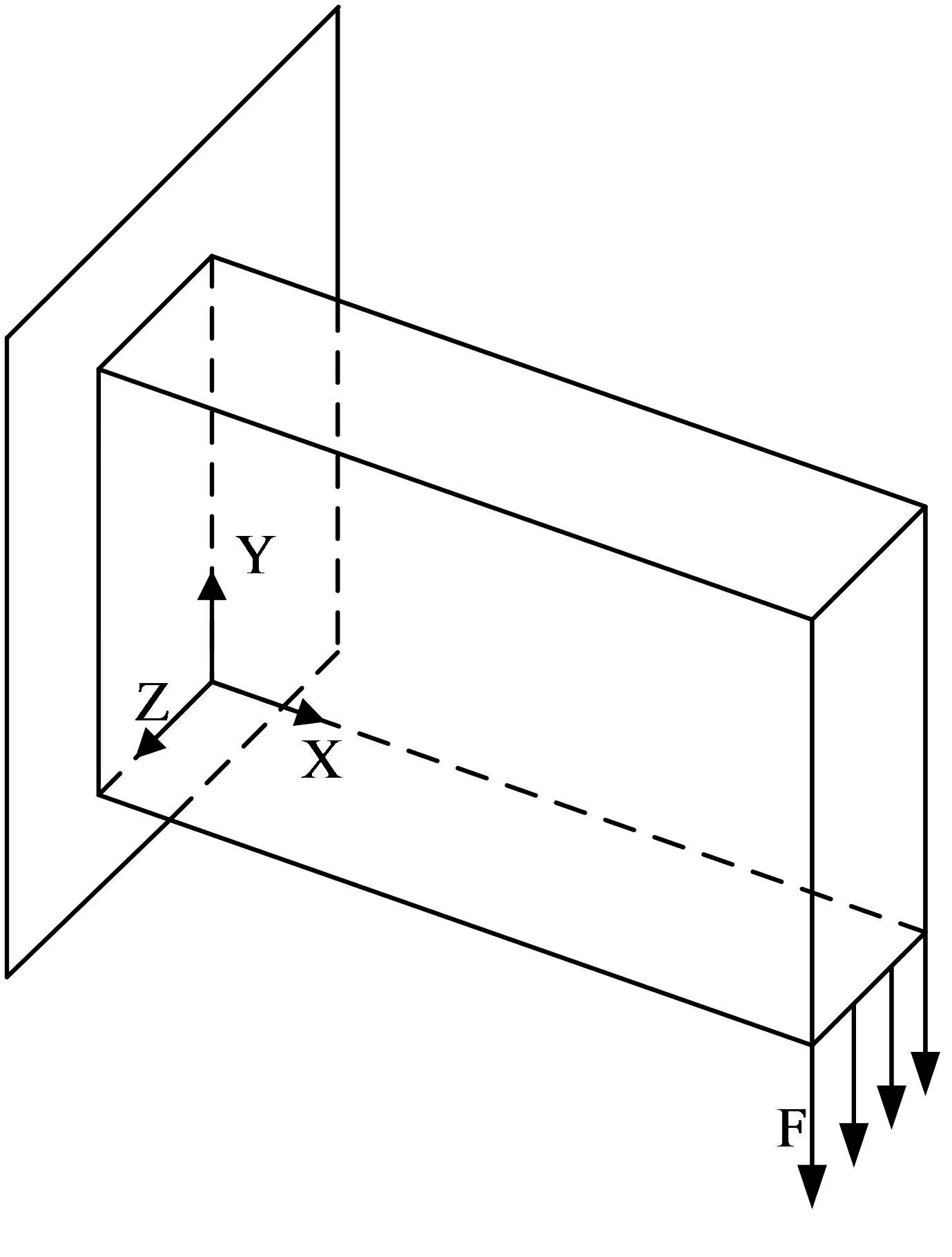
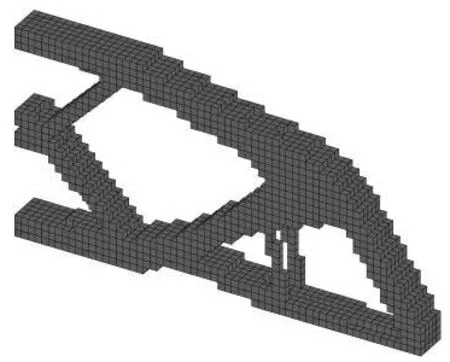
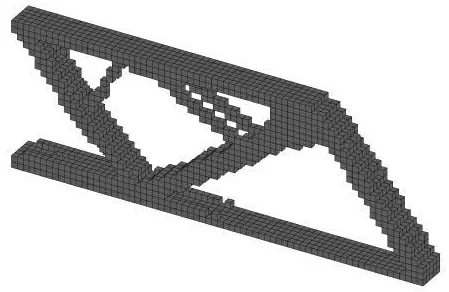
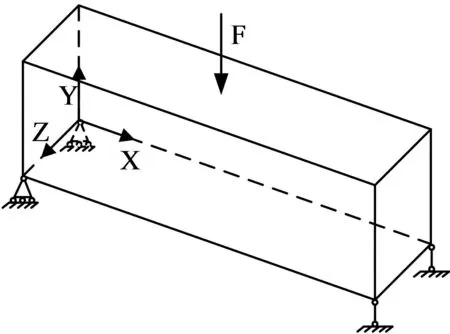
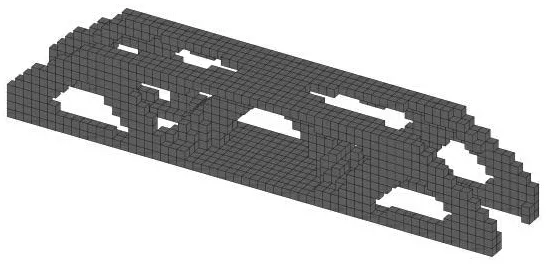
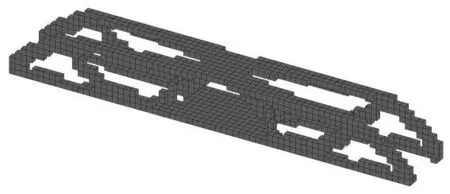
0

式中,C为结构的柔度,F为结构的力向量,U为结构的位移向量,xi为材料单元的相对密度,ui为材料单元的位移列向量,k0为材料密度为“1”的单元刚度矩阵,V(x)为材料体积,V0为设计体积,Vol为结构的容积率,xmin为最小材料单元密度,通常取为0.001.

建立模型后，使用优化准则法(Optimality Criterion,OC)求解式(14)的结构柔度最小问题,迭代计算后得出优化结果.

2.2.2 可靠度优化模型

在式(14)的拓扑优化模型中,并没有把可靠度指标考虑进去,这种优化方式在实际工程中难以应用,而且可能导致优化结果的可靠度不足.因此在可靠度拓扑优化模型中,需要将可靠度加入目标函数,即把式(5)引入式(14)可得：

Find:X={x1,x2,x3,…,xn}T∈Ω

Subjectto:β(u)≥βt

(15)

F=KU

0

对于此模型,在设计的参数中,要求先对非正态分布的随机变量进行当量正态化,变成正态分布的随机变量,然后利用β的几何意义迭代得到满足可靠度要求的随机变量.再继续用式(15)进行优化工作.这样的好处是可靠度优化和拓扑优化的分开进行,避免了两种优化耦合性影响计算速度.

3 计算结果与比较

3.1 算例一

悬臂梁给定的初始设计区域如图2所示,弹性模量E,泊松比μ,右下角有垂直向下的拉力F.

图2 悬臂梁初始设计域

悬臂梁的荷载F、外形尺寸及结构容积率Vol为非正态分布随机变量,它们的参数如表1所示.

表1 悬臂梁及带孔悬臂梁的几何参数

传统拓扑优化的设计参数为定值,因此按表1的均值计算,优化结果如图3(a)所示,考虑可靠度指标β=3.8(失效概率为2.9195×10-4)的拓扑优化结果如图3(b)所示.

(a)传统拓扑优化结果

(b)基于可靠度的优化结果

从图3中可以看出,结构的两种优化结果有很大区别,经过可靠度优化后的结构内部支撑分布更加合理,用料更加经济.在满足预定的结构性能要求的情况下,传统拓扑优化结构的体积为2 675 mm3,基于可靠度设计的结构体积仅为1 568 mm3,这表示考虑可靠度后的拓扑结构自重只有原来的60%,这不仅减少材料用量,还可以极大地降低生产成本.

3.2 算例二

在工程设计中,有时需要在结构上预留一些孔洞,因此在算例一的基础上,如图4(a)所示在悬臂梁的(3/X,2/Y,0)处预留一个直径为3/Y,厚度为Z的圆柱形孔洞,其余参数见表1,优化结果如图4(b)、4(c)所示:

(a)初始设计域

(b)传统拓扑优化结果

(c)基于可靠度的优化结果

在图4(b)所示的传统拓扑优化结果中,固定端多了一个支座用以加固中间孔洞,右上方通过曲面结构过渡到右下角,在实际工程中会增大施工难度.而图4(c)考虑可靠度指标β=3.8的优化结果中,仅用三根连杆对孔洞周围进行加固,结构分布更加合理,方便施工.在满足预定的结构性能要求的情况下,图4(b)的结构的体积为2 715 mm3,图4(c)结构的体积为2 150 mm3,这表示带孔悬臂梁考虑可靠度后的优化结构减少约20%的自重.在满足结构性能要求的前提下,结构的可靠度也大大增加,同时降低施工难度,结构设计更加合理.

3.3 算例三

简支梁的初始设计区域如图5所示,弹性模量E,泊松比μ,在结构(X/2,Y,Z/2)处有垂直向下的集中荷载F.

图5 简支梁初始设计域

简支梁的荷载F、外形尺寸以及结构容积率Vol为非正态分布随机变量,它们的参数如表2所示：

表2 简支梁的几何参数

传统拓扑优化的设计参数按表2的均值计算,优化结果如图6(a)所示,考虑可靠度指标β=3.8的优化结果如图6(b)所示.

(a)传统拓扑优化结果

(b)基于可靠度的优化结果

从图6中可以看出简支梁的可靠度优化结果比传统拓扑优化结果增加更多的杆件结构对内侧进行支撑,杆件结构分布合理,节约内部空间,也使结构更易于在实际工程中施工.图6(a)结构的体积为1 272 mm3,图6(b)结构的体积为1 016 mm3,可靠度优化在满足预计结构条件的同时减轻约20%的自重,减少生产成本,优化效果明显,也更符合在工程实际中应用.

4 结论

本文提出一种在三维结构中将可靠度分析与传统拓扑优化相结合的结构优化方法.建立结合JC法与变密度法的六面体单元可靠度优化模型.使用三维结构的几何尺寸、荷载以及容积率作为待优化的参数,并令其为非正态分布的随机变量,对三种常见静定梁结构进行优化分析.对比只能处理确定性参数的传统拓扑优化方法与可以处理非正态分布参数的可靠度优化方法的结果,对比结果表明,结合可靠度优化的三种常见静定梁结构的优化结果更加合理,拥有更多的杆件结构,易于施工.算例中结合可靠度优化的悬臂梁结构比传统优化方法减少40%的自重,带孔悬臂梁与简支梁结构均减少20%的自重, 在满足同样结构性能要求的前提下增加了结构可靠度,降低生产制造成本,优化效果明显.本文提出的基于结构可靠度的非正态分布条件下结构三维拓扑优化方法为工程结构优化提供了一种新的优化方法,具备工程应用价值.