一种改进的基于NSST-SPCNN医学图像融合算法
2021-05-12常春红王雷郝本利邢艺馨
常春红,王雷,郝本利,邢艺馨
( 山东理工大学 计算机科学与技术学院, 山东 淄博 255049)
医学图像融合将成像模态不同的多个医学图像,根据同一组织器官多种模态图像具有互补性与冗余性,使其成为一个新的图像,涵盖更丰富的细节及更全面信息,有助于医生更全面地了解病变的信息、性质及与周围解剖结构的关系。传统图像融合算法一般过程为图像分解、图像融合、图像重建。
对图像进行分解与重建的方法有很多,例如基于金字塔的方法[1]、非下采样轮廓波(NSCT)[2]、非下采样剪切波(NSST)[3]、稀疏表示[4]等方法,NSCT与NSST在图像细节表示方面有较高的恢复性,明显优于其他算法,而NSCT相对于NSST的计算复杂度较高,同时NSST具有移不变性与多方向选择性,可以更有效地提取源图像中的边缘信息、特征信息,以保留更多的源图像信息。
对图像分解之后得到高频图像与低频图像,选择合适的融合策略,分别对高频图像与低频图像进行融合是至关重要的。常见的图像融合规则有主成分分析(PCA)[5]、人工神经网络(CNN)[6]、脉冲耦合神经网络(PCNN)[7]、人类视觉系统等方法。主成分分析的方法未考虑图像各波段的特点,会丢失低分辨率图像的第一主成分中一些反应光谱特性的信息。人工神经网络以其独有的并行性与学习性,为我们提供了一种全新的数据融合方法;但在实际应用中,在网络结构设计与算法规则等方面,都有许多工作亟待解决。其中,脉冲耦合神经网络作为一种特殊的人工神经网络,基于猫的视觉原理构建的简化神经网络模型,由大量动态的脉冲耦合神经元互相连接组成的反馈型网络,不需要进行学习与训练,能够从复杂背景下获取有效信息,具有时空总和特性、动态脉冲发放特性和同步脉冲发放引起的振动与波动等特性[8]。由于传统PCNN模型的参数数量较多,且不同参数值的设置对图像效果有着至关重要的作用,后来Chen等[9]提出了一种自适应参数的SPCNN,根据图像本身的特性信息自适应设置PCNN的各个参数。该方法具有较强的适应性,但是需要对每个像素点的链接强度参数进行计算,计算量大,影响融合速度。
为了对使用PCNN模型融合时的参数进行有效确定,根据参数特性与模型特点,提出了一种新的改进自适应参数PCNN的方法,对多种模态医学图像进行融合。
1 融合的原理

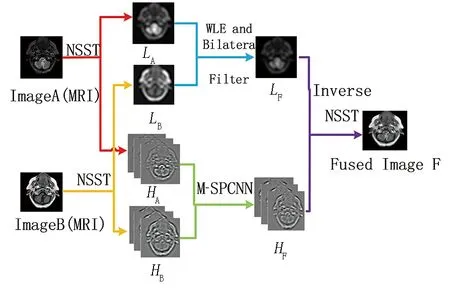
图 1 NSST-M-SPCNN 图像融合过程Fig.1 Image fusion process of NSST-M-SPCNN
2 融合的规则
2.1 低频区域局部能量加权和与双边滤波融合规则
低频分量主要对整副图像强度综合度量,一幅图像的能量一般保存在低频分量中,对低频分量的融合一般采取简单平均或者加权平均的方法,容易造成图像细节信息与能量的丢失,从而降低源图像的对比度[10]。
根据某一区域内,各像素点之间具有较强的相关性。本文先采取局部区域能量加权和规则,最大限度保留源图像的能量,如公式(1):
(1)
式中:S∈{A,B};L(i,j)为源图像在位置(i,j)的低通分量;W为一个(2r+1)(2r+1)的加权矩阵,将矩阵元素设置为22r-d;d为其到矩阵中心四邻域的距离。
为了最大限度获取源图像的细节信息,采用双边滤波规则。双边滤波是一种非线性滤波方法,为了对图像实现保边去噪,既考虑了图像的空域信息又考虑了灰度相似性。双边滤波通过空域矩阵和值域矩阵形成一个新的权重矩阵,其中空域矩阵用来模糊去噪;值域矩阵用来保护边缘[11]。
设(i,j)为源图像的中心点坐标,(k,l)为以(i,j)点为中心的邻域S内的任意一点,空域矩阵中点(k,l)到点(i,j)的空间距离定义为
(2)
值域矩阵定义为
(3)
公式(2)与(3)相乘后,会产生对数据依赖的双边滤波权重矩阵
(4)
最后,计算点(k,l)到点(i,j)新的像素值
(5)
空间距离D函数按照像素之间的距离选择权重,距离越远权重越小,越近越大。值域矩阵R函数是按照像素值之间的差异进行权值分配。在比较的平坦区域,像素之间的差异比较小,其所对应的值域权重R(i,j,k,l)接近于1,故此时起主要作用的是空域权重D(i,j,k,l),相当于对这个平坦的区域直接进行了高斯模糊。图像边缘的特点就是距离相近的点的像素值有很大差异,滤波的同时保留边缘,即在边缘区域,像素之间差异较大,即f(k,l)-f(i,j)之间差值大。根据公式(4)可以看出,此时的值域核权重相对会变小,会导致此处的总权重值W(i,j,k,l)下降,当前像素点(i,j)受到大的差异像素点的影响就越小,进而保持了边缘的细节信息。
最后,可通过公式(6)来计算融合的低频分量图像。
LF(i,j)=
(6)
采用这两种方法结合,既提取了图像强度(亮度/灰度)变换平缓部分(低频分量)的细节,又保留了源图像低频系数的能量。
2.2 高频区域简化自适应参数PCNN融合规则
神经元是构成神经网络的基本单元,模型的大小与被处理图像的大小是一致的,PCNN模型中的每一个神经元分别对应图像中的每一个像素点,每个神经元接收到的外界刺激即为该像素的灰度值。脉冲耦合神经网络模型的结构如图2所示。
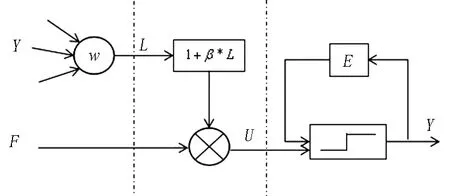
图 2 脉冲耦合神经元模型Fig.2 Pulse coupled neuron model
图2中:F为反馈输入,是从神经元收到的最主要的输入;L为连接输入,是从与当前神经元相连接的临近神经元接收到的次要输入;Y为输出。由图2可以看出,一个神经元模型主要由输入部分、输出部分和脉冲发生器组成。Chen等[9]提出的一种自适应参数的SPCNN模型如方程(7)描述:
(7)
其中:Fij(n)、Lij(n)是在图像(i,j)处迭代n次的反馈输入、连接输入;Sij为外部刺激;Uij为内部活动项;Eij为动态阈值;Yij是输出;β为连接强度;VL、VE分别为连接输入与动态阈值的振幅;αf、αe分别为反馈输入与动态阈值的指数衰减常数;W为连接输入的突出连接矩阵即中心像素与邻域像素的连接权矩阵。由模型方程可以看出,存在5个自由参数,分别为β、VE、VL、αf、αe,根据文献[9]中的分析,所有的参数可以根据图像本身的特性,自适应定义为公式(8)—公式(11):
αf=log(1/σ(S)),
(8)
(9)
VE=exp(-αf)+1+6βVL,
(10)
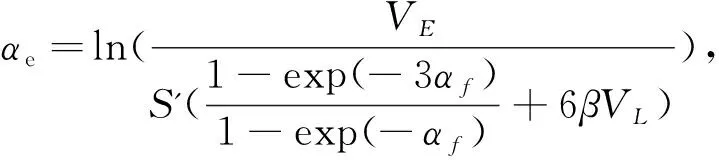
(11)
式中:Smax为输入图像的最大强度值;S'为归一化的大津阈值;VL的取值一般为1或随机值;σ(S)为图像样本的标准差。图像的标准差反映了图像的整体结构特征,如果一幅图像整体灰度值变化不大,方差就会小,那么神经元更容易保持前一状态,反之亦然。
受SPCNN模型的启发,为了提高融合的效率与质量,降低计算的复杂度,提出了一种改进的SPCNN算法(M-SPCNN),算法模型如下:
(12)
用公式(12)表示的M-SPCNN模型处理耦合连接的图像时,神经元能否被捕获取决于神经元所对应像素的灰度值、连接强度、点火时间,其中连接强度中的突出权重Wijkl与所选取的邻域大小有关,本文采用常用的8邻域计算:
(13)
描述耦合连接的M-SPCNN模型是迭代方差,当前方程和上一次迭代输出的状态有关,M-SPCNN点火原理如下:
设所有的神经元初始状态均为
Uij(0)=0,Eij(0)=0,Yij(0)=0。
①当n=1时:
(14)
Eij(1)=0,
(15)
此时Uij(1)>Eij(1),可以得出Yij(1)=1,与输入图像非零像素对应的神经元点火,第一次迭代点火也是无效点火。
②当n=2时:
(16)
Uij(2)=Sij(1+6β),
(17)
Eij(2)=VE。
(18)
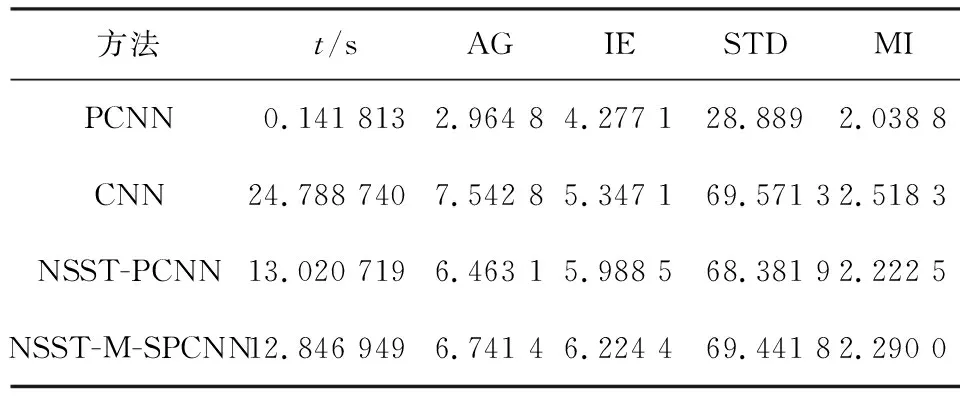
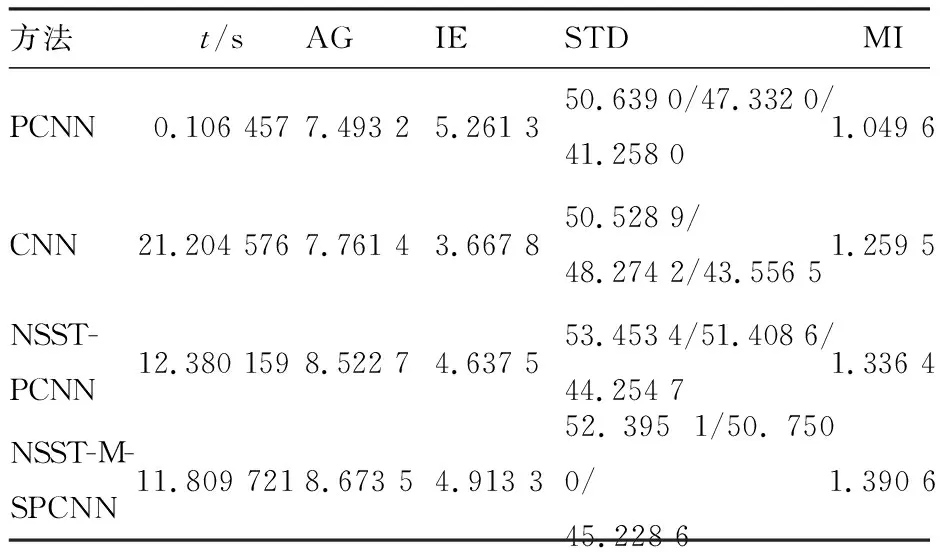
由于上一次神经元点火,导致此刻的动态阈值达到一个很高的值,即此时Uij(2) 对比SPCNN模型可以看出,M-SPCNN模型的参数只有连接强度β、动态阈值的衰减常数αe与振幅VE。 β代表了邻域神经元之间的连接强度,其值越大,说明邻域神经元之间的影响就越大,Uij越剧烈,反之亦然。PCNN模型处理图像的过程一般是,通过输入合适的参数值,使其在同一个区域内的像素点在同一个时刻点火,在不同区域内的像素点在不同时刻点火。 根据文献[12]中提出的将图像分为背景区域和目标区域,自适应选择合适的连接强度β。设R、B分别为目标区域、背景区域所对应的神经元的集合,则其灰度范围为[SRmin,SRmax]、[SBmin,SBmax],且SRmax>SBmax。当SBmax>SRmin时,说明目标区域与背景区域有重合的部分。完美的图像融合,就是要在SRmin点火的时候SBmin不点火,即满足以下三个特征[13]: ①SRmin在n=T(SRmax)时刻点火,SRmin(1+βLRmin)≥SRmax; ②SBmin在n=T(SBmax)时刻点火,SBmin(1+βLBmin)≥SBmax; ③SBmax在n=T(SRmin)时刻不会点火,SBmax(1+βLRmax) 由以上三个条件可以得出: (19) (20) 因为完美的状态是很难达到的。因此要选择一个合理的β值,并且在计算的时候不需要很复杂的图像后验信息。本文选择βmax作为参数β的值,且SRmax与图像最大灰度值Smax一致,而不同的图像的SBmax是不同的,本文采用大津阈值法代替SBmax。又因为8邻域时,连接输入的最大值为6,故式(19)可以表示为 (21) 动态阈值振幅VE影响融合的宽度,衰减常数αe影响动态阈值E的衰减速度,αe越小精度越高,相对消耗的时间就长。M-SPCNN迭代时,需要满足Uij(n)>Eij(n)时点火,不满足则不点火。设当前迭代的时刻为t,S∈[Slow,Shigh]的神经元可点火,此时: (22) 根据模型公式(12)可以得到: Shigh(1+βLhigh(t-1))≤E(t-1), (23) Slow(1+βLlow(t))>E(t), (24) (25) 由于前面假设了M-SPCNN模型第一次迭代时,所有的神经元均点火,第二次迭代时,所有神经元均不点火,所以在第三次迭代时: (26) 第一次点火被看作无效点火,所以第一次有效点火为第三次迭代,希望能粗略得到图像的目标区域。此时该区域的灰度值应该是目标区域的最大灰度值到图像最大灰度值,即SBmax (27) 可得到: (28) (29) 由VE=Smax(1+6β)可得 (30) 根据M-SPCNN模型公式(12),点火时间可以在每次迭代结束后通过以下公式累计获得: Tij(n)=Tij(n-1)+Yij(n) (31) (32) 即选择点火次数最大的系数作为融合的高频系数。 为了验证本文提出算法的有效性,分别选用四组已配准的CT-CT、MR-CT、MR-MR、MR-PET的图像进行融合实验。同时,本文算法与传统PCNN融合(β=0.5,αf=0.012,VL=1,VE=4000)、NSST-PCNN融合[14]、CNN融合等算法进行比较,从主观与客观两个角度评价融合的质量,从主观上融合的结果,如图3所示。客观上,分别使用平均梯度、信息熵、标准差、互信息等客观评价指标定量分析的融合结果见表1—表4。 ImageAImageBPCNNCNNNSST-PCNNNSST-M-SPCNNCT-CTMR-CTMR-MRMR-PET 从视觉效果上看,本文算法的清晰度与分辨率较其他算法高,既保留了两幅源图像的大部分信息,又突出了边缘与细节信息,明显优于其他算法,说明了本算法具有可行性、适应性、有效性等。由定量分析的结果可以看出,本文算法的各项指标大都高于其他方法。其中,平均梯度反映了图像的微小细节与纹理特征;信息熵代表了图像携带信息量的多少,信息熵越大说明了携带的信息量越大;标准差的大小可以反映出图像对比度的大小,标准差越大,图像的反差大,对比度就越大;互信息表示源图像有多少信息转移到了融合后的图像中,越大代表了包含源图像的信息量越大,效果越好。 表1中PCNN融合的速度最快,因为此时的PCNN参数是根据经验值设置的,没有多余的计算,故而时间融合速度最快,但从图3中可以看出,PCNN的融合效果也是最差的。除此之外,无论是视觉效果,还是定量分析的结果,本文算法都明显优于其他算法。 表4中的标准差定量分析中,每个算法的标准差分别有三个值,pet与融合后的图像是彩色图像,代表了在融合图像在xyz三个方向上的标准差。 表1 MR-CT模态融合的评价指标结果Tab. 1 Evaluation index results of MR-CT modal fusion 表2 CT-CT模态融合的评价指标结果Tab. 2 Evaluation index results of CT-CT modal fusion 表3 MR-MR模态融合的评价指标结果Tab. 3 Evaluation index results of MR-MR modal fusion 表4 MR-PET模态融合的评价指标结果Tab. 4 Evaluation index results of MR-PET modal fusion 1)低频区域,采用的局部区域能量加权和规则以最大限度保留源图像的能量,双边滤波方法在去噪的同时充分提取源图像的细节信息。两种方法结合,既保留了源图像低频系数的能量,又最大限度地提取了图像强度(亮度/灰度)变换平缓部分(低频分量)的细节。 2)在高频区域内,采用改进的自适应PCNN算法,简化SPCNN模型,减少参数的数量,提高了融合的效率;同时,保持了PCNN非线性调制耦合、阈值可变及加权求和等特性,能从复杂背景下获取有效信息。 实验结果表明,本文所提出的改进算法可以有效地保留图像中的细节信息,充分地保存纹理特征,保持图像边缘与纹理清晰,与传统算法相比,具有更好的性能与适用性。
2.3 NSST重建
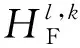
3 实验结果分析



4 结论
