基于改进ADC模型的通信对抗系统作战效能评估
2021-05-12汪慧阳刘松涛
汪慧阳,刘松涛,赵 帅
(海军大连舰艇学院信息系统系,辽宁 大连 116018)
0 引言
通信对抗系统作战效能评估,能够为通信对抗技术的研究以及系统的改进和使用提供依据。系统作战效能是指系统在规定条件下满足特定作战任务需求的程度,是一个具有相对性、时效性和概率性的值[1]。因此,在对系统作战效能评估时,需要考虑特定的任务目标和特定的使用环境。当前,已有许多方法应用到系统作战效能评估研究中,如模糊评判法、多属性决策法、ADC(availability dependability capability)模型法等。其中ADC模型法是一种成熟的效能评估方法,综合性强,比较适合通信对抗系统作战效能的评估[2]。但它没有较好地结合任务的实际过程,也没有考虑外部影响系统使用的因素。
针对此问题,许多改进ADC模型被提出。目前已有的改进模型主要可分为两类。一类是添加新的评估要素。文献[3]中对便携式通信对抗装备评估,考虑到其功率小、机动性弱、受装备操作人员和战场环境影响明显,在ADC模型中引入了作战操作人员M和战场环境影响G。这种引入新的评估要素的改进模型,直接将引入的因素与原有评估要素相乘,没有将引入的评估要素与原有的评估因素作主次之分,会造成新引入的影响因素对评估结果影响过大,而导致某些情况下评估结果不准确。另一类是改进现有的评估要素。文献[4]中主要针对可用度要素A,在正常和故障之间增加了中间状态,在状态描述和状态转移方面均做了改进;文献[5]将评估对象分为三个在所处状态概率上相互独立的分系统,对可用度A和可信度D进行了改进;文献[6]利用生灭过程来描述时间连续状态有限的状态转移过程,提出BDP-ADC(birth and death process-ADC)模型;文献[1]在建立可用度向量和可信度矩阵时,考虑系统单元的串并联关系,将系统分为多种状态;文献[7]考虑了四季以及时段对效能的影响,将效能E按所处的季节和时段构成了效能矩阵;文献[8]将固有能力C的求解同指数法相结合。上述这类改进方法更加细致地分析了系统的状态、能力等,但在评估时,存在没有结合实际作战过程的问题。本文针对此问题,将通信对抗实施过程分为三个阶段:搜索截获阶段、测向阶段和干扰阶段,再将可用度向量A和可信度矩阵D结合起来进行改进分析,提出基于改进ADC模型的通信对抗系统作战效能评估模型。
1 ADC模型及其改进
ADC模型[9-10]强调了装备的整体性,为效能评估提供了一个基本框架,容易进行拓展,比较适合环境复杂的通信对抗系统作战效能评估。ADC模型评估的三大要素为可用度(availability)、可信度(dependability)和固有能力(capability)。其效能评估结果E由三大评估要素组合得出,表达式为:
E=A·D·C
(1)
式(1)中,E为通信对抗系统作战效能;A为系统可用度向量,表示系统在任务开始时,处于可能的几种状态的概率,能够体现出系统待命的能力;D为系统可信度矩阵,表示已知系统在任务开始时的状态,在执行任务时所处状态的概率,能够体现出系统在任务中的稳定程度;C为系统的固有能力向量,表示系统完成任务的能力,能够体现出系统的性能。
通信对抗实施是一个动态过程,不同阶段执行的具体任务不同,因此,为了更准确地描述可用度和可信度,本文将通信对抗系统执行任务分阶段考虑,分为搜索截获阶段、测向阶段和干扰阶段,并分别对应三个分系统。之所以分阶段考虑,一是因为过程中各分系统存在单向影响关系,某个阶段出现问题,可能影响的不仅仅是一个过程,也会对后续的过程产生影响,如搜索截获阶段出现问题,则会影响到后续的测向和干扰过程;二是因为对每个分系统的评估时间也不同。
对可用性向量和可信度矩阵的具体改进思路为:假设三个分系统状态相互独立,按照系统在执行任务时划分的三个阶段,每个分系统被评估的时长也不同。对于完成任务,需要保证的是各分系统在各自阶段是处于正常状态或是从故障状态转为正常状态。比如,在一次任务中,如在任务开始时状态为搜索截获系统正常,测向和干扰系统故障,那么在搜索截获阶段,测向和干扰系统的故障对任务是没有影响的,测向系统只需保证在测向阶段可以修好即可,干扰系统同理;并且每阶段完成后,不再考虑该系统。上述分析意味着要分阶段考虑系统的可用度和可信度,如图1所示。

图1 任务阶段性流程Fig.1 Task phased process
1) 搜索截获阶段
该阶段也是任务开始的阶段,根据各分系统处于故障或正常状态,系统可分为8种状态[5],各状态及对应的概率如表1所示。

表1 系统状态及概率Tab.1 States and probabilities of system
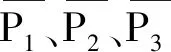
(2)
式(2)中,MTBFi为第i个分系统的平均故障间隔时间,MTTRi为第i个分系统的平均修复时间。该阶段可用度向量为:
A1=[a1,a2,a3,a4,a5,a6,a7,a8]
(3)
假设系统在执行任务中是可修复的,且故障和维修均服从指数分布,三个分系统的故障率分别为λ1、λ2、λ3,维修率分别为μ1、μ2、μ3,三个分系统在搜索截获阶段保持正常的概率分别为S1、S2、S3,修复成功的概率分别为F1、F2、F3,搜索截获阶段的时长为T1,dij为系统从状态yi转为状态yj的概率,则:S1=e(-λ1T1),S2=e(-λ2T1),S3=e(-λ3T1),F1=1-e(-μ1T1),F2=1-e(-μ2T1),F3=1-e(-μ3T1),d11=S1·S2·S3,d12=S1·S2·(1-S3),d21=S1·S2·F3,d22=S1·S2·(1-F3)。
其余依次类推,可得搜索截获阶段的可信度矩阵为:
(4)
2)测向阶段
测向阶段的起始时刻即搜索截获阶段的结束,因此,该阶段的可用度应结合上一阶段的可用度和可信度。上阶段结束时的系统状态向量为:
(5)
根据前文分析,只有在前三个状态和第五个状态,搜索测向分系统处于正常状态,即只有这几个状态能够完成前一阶段的任务。因此,测向阶段开始时刻的可用度向量为:
(6)
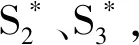
其余以此类推,可得测向阶段的可信度矩阵为:
(7)
3)干扰阶段
干扰阶段的起始时刻即测向阶段的结束,因此该阶段的可用度同样应结合上一阶段的可用度和可信度。测向阶段结束时系统状态向量为:
(8)
因为只有在前两个状态,测向分系统处于正常状态,测向任务才能完成。因此,干扰阶段开始时刻的可用度向量为:
A3=[a′1,a′2]
(9)
该阶段仅需关注干扰分系统的状态,设干扰分系统在该阶段保持正常的概率为S′3,修复成功的概率为F′3,该阶段时长为T3,d′ij为系统从A3中a′i对应的状态转为a′j对应的状态的概率,则S′3=e-λ3(T1+T2+T3),F′3=1-e-μ3(T1+T2+T3),d′11=S′3,d′12=1-S′3,d′21=F′3,d′22=1-F′3。
可信度矩阵为:
(10)
2 通信对抗系统作战效能评估指标分析及计算
2.1 通信对抗系统作战效能评估指标体系
为了准确评估通信对抗系统作战效能,结合改进的ADC模型和上述通信对抗实施过程,分析建立比较完善的评估指标体系,如图2所示。系统可用度由系统的平均故障间隔时间和平均修复时间两个指标构成;系统可信度由系统的故障率和修复率两个指标构成;固有能力由搜索截获能力、测向能力和干扰能力三个指标构成。其中,系统可用度和可信度的具体计算已在前文ADC模型改进中描述,下文主要介绍固有能力的指标计算。
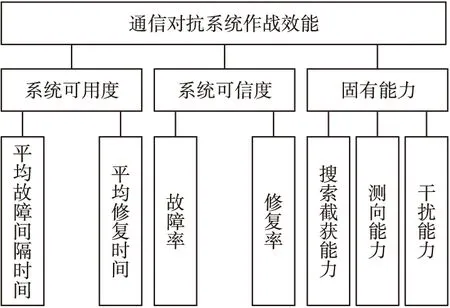
图2 评估指标体系Fig.2 Evaluation index system
2.2 系统固有能力
根据上述对可信度和可用度的分阶段分析,通信对抗系统在执行任务时有8种状态,因此,其固有能力矩阵为C*=[c1,c2,c3,c4,c5,c6,c7,c8]T。只有当三个系统都在相应阶段正常时才能够顺利完成任务,因此,最终的能力矩阵为C=[c1,0]T,c1为任务能够完成的情况下,系统的固有能力。
接下来分析完成任务时的固有能力c1。根据通信对抗系统的使命任务,本文考虑了搜索截获能力U1、测向能力U2和干扰能力U3三个因素[11]。为了能够定量评估系统固有能力,需要将各评估指标无量纲归一化处理,取最优为1,最差为0。c1计算公式为:
(11)
式(11)中,ωi为权重系数,i=1,2,3。
(12)
式(12)中,当i=1时,n=3;当i=2时,n=2;当i=3时,n=4;Uij为Ui的下层指标;ωij为权重系数,表示了该指标对上层指标的重要程度,具体的值由层次分析法结合专家打分得出。
2.2.1搜索截获能力
通信对抗系统的搜索截获能力受侦察频率范围、侦察截获概率和侦察作用距离限制。由式(12)可得搜索截获能力为:
U1=ω11U11+ω12U12+ω13U13
(13)
1)侦察频率范围U11
侦察频率范围U11由系统实际的侦察频率范围(r1,r2)与任务的侦察频率范围(R1,R2)相比得出,表示为:
(14)
式(14)中,r2、r1分别为系统实际侦察频率范围的上下限;R2、R1分别为任务的侦察频率范围上下限。
2)信号截获概率U12
侦察截获概率U12由实际截获目标信号数m与应截获目标信号数m0相比得出,表示为:
(15)
3)侦察作用距离U13
侦察作用距离U13要根据实际任务情况[12-13],由实际侦察作用距离d与任务所需侦察探测距离d0相比得出,表示为:
(16)
2.2.2测向能力
通信对抗系统的测向能力受到测向精度和测向反应时间的限制。由式(12)可得测向能力为:
U2=ω21U21+ω22U22
(17)
1)测向精度U21
测向精度U21表示实际测向值与真值的接近程度,表示为:
(18)
式(18)中,f0为任务可接受最大测向误差,f1为实际测向误差。当实际测向误差f1大于可接受最大误差f0时,认为测向精度为0。
2)测向反应时间U22
测向反应时间U22为测向所需的信号最短持续时间,表示为:
(19)
式(19)中,τ为系统执行任务时,测向所需信号最短持续时间;τ0为任务理想的信号最短持续时间;τm为任务可接受最短持续时间的最大值。
2.2.3干扰能力
通信对抗系统的干扰能力受干扰功率、时域覆盖率、频域覆盖率和多目标干扰能力限制。本文描述的干扰能力为阻塞式干扰能力。由式(12)可得干扰能力为:
U3=ω31U31+ω32U32+ω33U33+ω34U34
(20)
1) 干扰功率U31
干扰功率的大小对干扰效果的好坏有着直接的影响,干扰功率如果达不到要求,对敌方的干扰效果就会很差。因此,可以根据任务需要,来评估干扰功率U31,表示为:
(21)
式(21)中,W为通信对抗系统实际最大干扰功率,W0和Wmin分别为根据任务需要所确定的最优干扰功率和任务可以接受的最小干扰功率。
2) 时域覆盖率U32和频域覆盖率U33
时域覆盖率U32和频域覆盖率U33分别表示了干扰信号在时域和频域的对准程度,二者都是区间型指标,归一化方法相同[14]。时域覆盖率表示为:
(22)
式(22)中,t1为干扰开始时间,t2为干扰终止时间,T2和T1分别是最佳干扰时间区间的上下限。同理,频域覆盖率表示为:
(23)
式(23)中,q2和q1分别为系统干扰频率上限和下限,Q2和Q1分别为任务最佳干扰频率区间上限和下限。
3) 多目标干扰能力U34
多目标干扰能力U34是指通信对抗系统能够同时有效干扰多个目标的能力,可表示为:
(24)
式(24)中,n为系统能够同时干扰目标批数,n0为任务所需干扰目标批数。
3 仿真实验分析
本文假设三个分系统的平均故障间隔时间为MTBF1=MTBF2=MTBF3=100 h,平均修复时间分别为MTTR1=2 h,MTTR2=0.5 h,MTTR3=1 h,故障率分别为λ1=0.02,λ2=0.05,λ3=0.03,维修率分别为μ1=0.7,μ2=0.75,μ3=0.65,一次任务中三个分系统的工作时长分别为T1=2 h,T2=0.5 h和T2=1 h。则系统可用度向量和可信度矩阵分别表示为:
A1=[0.965 9,0.009 7,0.004 8,0.019 3,
4.8×10-5,0.000 2,0.000 1,9.7×10-7]
(25)
(26)
A1·D1=[0.812 9,0.052 2,0.086 1,0.036 8,0.005 5,0.002 4,0.003 9,0.000 3]
(27)
因为第一阶段是搜索截获阶段,所以搜索截获分系统必须处于正常状态或从故障状态转为正常状态。因此只有前三个状态和第五个状态有效。那么第二阶段可用度向量为和可用度矩阵分别表示为:
A2=[0.812 9,0.052 2,0.086 1,0.005 5]
(28)
(29)
(30)
因为第二阶段是测向阶段,所以测向分系统必须处于正常状态或从故障状态转为正常状态。因此,只有前两个状态有效,那么第三阶段的可用度向量和可信度矩阵分别表示为:
A3=[0.773 9,0.067 1]
(31)
(32)
A3·D3=[0.757 0,0.084 0]
(33)
因为第三阶段是干扰阶段,所以干扰分系统必须处于正常状态,或从故障状态转为正常状态。因此只有第一个状态有效。那么最终系统能够以正常状态完成任务的概率为0.757 0。
接下来分析系统的固有能力,各级指标权重如图3所示。

图3 各级指标权重Fig.3 Weight of indexes at all levels
为了验证评估模型的可行性,假定装备实际使用值和理论参考值如表2所示。将表中参数代入评估模型中,得到c1=0.762 9,将其代入式(1)得到系统作战效能E=0.577 5,实现了系统作战效能的定量评估。

表2 装备实际使用值和理论参考值Tab.2 Actual use value and theoretical reference value of equipment
为了验证分阶段考虑更加贴近实际,分别通过改变系统的可靠等级(故障率和修复率)和工作时长设置,将分阶段模型与非阶段模型进行对比。仿真结果如图4和图5所示,可靠等级参数设置如表3所示,表中最后两列分别为非分阶段模型的故障率λ和修复率μ,是按照各分系统工作时长之比,加权求得;各分系统工作时长和非分阶段模型中系统的工作总时长设置如表4所示,表中Tt为非分阶段模型的工作总时长。

图4 作战效能随可靠等级变化Fig.4 Operational effectiveness varies with reliability level

图5 作战效能随工作时长变化Fig.5 Operational effectiveness varies with working hours

表3 可靠等级参数Tab.3 Parameters of reliability level

表4 工作时长参数Tab.4 Parameters ofworking hours
分析结果可知,非分阶段考虑的模型,只是单一地根据整个系统在任务完成时的最终状态,来判断能否完成任务,忽略了中间状态对任务的重要的影响,得到系统作战效能比实际的要高,而随着系统的可靠等级提高或工作时长的增加,二者的差距将会逐渐缩小。因此,分阶段考虑的模型更贴近实际。
4 结论
本文提出基于改进ADC模型的通信对抗系统作战效能评估模型。该模型根据通信对抗系统的实际作战过程,对传统ADC模型的应用进行了改进,着重对可用度向量和可信度矩阵进行了分系统、分阶段详细地描述与改进。在具体分析计算评估指标时,细化到对每个底层评估指标进行量化,所得出的结论更加精确合理。仿真实验分析表明,改进模型克服了传统ADC模型没有结合作战实际过程,状态描述粗略的缺点,更加贴近实际,提高了通信对抗系统作战效能定量评估水平,其评估结果能够为通信对抗系统的运用和改进提供参考。
