基于偏最小二乘与随机森林的土壤盐含量反演研究

肖志云 徐新宇

摘要 針对土默川平原地区的土壤盐分含量提出了偏最小二乘与随机森林相结合（RF-PLSR、PLSR-RF）对土壤盐分含量进行预测的回归反演模型。该研究共采集45份土壤样本，随机选取35份为建模集，10份为验证集。试验首先对采集到的高光谱土壤图像进行分割处理提取出土壤在400～1 000 nm的原始反射光谱，其次对原始反射光谱进行4种光谱变换（一阶微分、多元散射校正的一阶微分、SG平滑去噪的一阶微分、对数的一阶微分），并与土壤的实测盐分量进行相关性分析（CA），利用相关系数选取敏感波段，最后建立偏最小二乘与随机森林结合的回归反演模型。结果表明，与偏最小二乘回归、随机森林回归单独建模相比，2种模型结合后的预测精度有明显的改善。光谱经过对数的一阶微分变换建立的PLSR-RF反演模型更为明显，其建模集决定系数Rc2为0.852，均方根误差RMSEc为0.102 g/kg，相对分析误差RPDc为2.600，验证集决定系数Rv2为0.941，均方根误差RMSEv为0.049 g/kg，相对分析误差RPDv为4.117。

关键词 高光谱;土壤盐含量;光谱变换;偏最小二乘回归;随机森林回归

中图分类号 TP391.4;TP79文献标识码 A

文章编号 0517-6611（2021）08-0010-06

doi：10.3969/j.issn.0517-6611.2021.08.004

开放科学（资源服务）标识码（OSID）：

Research on Inversion of Soil Salt Content Based on Partial Least Squares Combined with Random Forest

XIAO Zhi-yun1，2，XU Xin-yu1，2 （1.College of Electric Power，Inner Mongolia University of Technology，Huhhot，Inner Mongolia 010080;2.Inner Mongolia Key Laboratory of Mechatronic Control，Huhhot，Inner Mongolia 010051）

Abstract Aiming at the soil salt content in the Tumochuan Plain，a regression inversion model combining partial least squares and random forest （RF-PLSR，PLSR-RF） to predict soil salt content was proposed.A total of 45 soil samples were collected in the study，35 of which were randomly selected as the modeling set and 10 of which were randomly selected as the verification set. The experiment first performed segmentation processing on the collected hyperspectral image of the soil to extract the original reflection spectrum of the soil at 400-1 000 nm，and then performed 4 kinds of spectral transformations on the original reflection spectrum （first-order differential，first-order differential of multiple scattering correction，SG smoothing Denoising first-order differential and logarithmic first-order differential）. And it performed correlation analysis （CA） with the measured salt content of the soil，utilized the correlation coefficient to select the sensitive band，and finally established a regression model combining partial least squares and random forest. Compared with partial least square regression and random forest regression，the prediction accuracy of the combination of the two models was significantly improved. The PLSR-RF inversion model that established by the first-order differential transformation of the spectrum was more obvious. Its modeling set determination coefficient Rc2 was 0.852，the root mean square error RMSEc was 0.102 g/kg，and the relative analysis error RPDc was 2.600. The set determination coefficient Rv2 was 0.941，the root mean square error RMSEv was 0.049 g/kg，and the relative analysis error RPDv was 4.117.

Key words Hyperspectral; Soil salt content; Spectral transformation;Partial least squares regression; Random forest regression

土壤盐碱化是目前世界面临的最主要的环境问题之一，直接影响着农业的可持续发展，而土默川平原地区是内蒙古主要的粮食生产基地之一，由于特定的水文地质条件、不合理的耕作和灌溉系统，该地区出现了大面积的盐碱地[1]。土地盐渍化问题变得越来越严重，这严重影响了该地区农牧民的收入和农业生产[2]。因此研究土壤盐含量具有重要的意义。

随着光谱技术的发展，越来越多的学者利用光谱技术对土壤盐含量进行了一定的反演研究[3-8]，Farifteh等[9]研究发现土壤盐分含量与光谱反射率之间存在显著相关性，表明光谱之间的相似性随土壤中盐分浓度的增加而降低。Srivastava等[10]证明了光谱反射率对盐度变化非常敏感。张智韬等[11]引入敏感波段组、光谱指数组、全变量组作为模型输入变量，并建立了4种反演模型，通过对比分析得出基于光谱指数组的随机森林盐分反演模型在12个模型中反演效果最佳。陈俊英等[12]利用无人机搭载六波段多光谱相机和热红外成像仪获取大田葵花土壤的遥感数据，并同步采集区域内不同土壤深度处的盐分数据;通过建立反演模型得出盐分指数和光谱指数作为变量组构建的模型效果优于植被指数变量组，且建立的支持向量机、反向传播神经网络、极限学习机等机器学习盐分反演模型比传统偏最小二乘方法较优。马利芳等[13]利用在新疆阜康市实测的VIS-NIR光谱通过相关性分析选取特征波段建立的RF模型具有很好的预测效果。张贤龙等[14]对原始光谱进行15种光谱变换，并构造光谱指数对土壤盐分含量进行反演，得出基于倒数的对数光谱变换构建归一化植被指数建立的土壤盐分反演模型精度最高。马驰[15]对采集到的HJ-1A高光谱影像数据进行大气校正，并对校正之后的光谱进行多种数学变换，结果表明一阶微分和倒数的一阶微分可以提高土壤反射率与实际盐分含量的相关系数。

综上所述，国内外针对土壤盐分含量进行的高光谱反演已经做了一定的研究，肯定了高光谱在预测土壤盐分含量的可行性。大多数都是采用多种光谱变换之后建立的回归预测模型，其模型反演精度低，而利用多种光谱变换建立的2种回归模型相结合反演土壤盐含量的研究很少，所以该研究提出了用2种算法相结合的预测模型，首先对采集到的高光谱土壤图像样本进行处理，提取出土壤的原始光谱数据，其次对其进行多种光谱变换，通过与实测土壤盐分含量进行相关性分析，选出敏感波段，最后建立偏最小二乘回归、随机森林回归及2种模型相结合的回归反演模型，以期为指导农田种植提供参考。

1 材料与方法

1.1 研究区概况 察哈尔右翼中旗位于内蒙古自治区乌兰察布市，土壤类型为砂质土，农田土壤适宜马铃薯、玉米等多种农作物种植，耕种制度为一年一熟。该试验研究地区位于察哈尔右翼中旗马铃薯示范基地，是内蒙古马铃薯高产高效理论应用技术创新团队的实验基地。

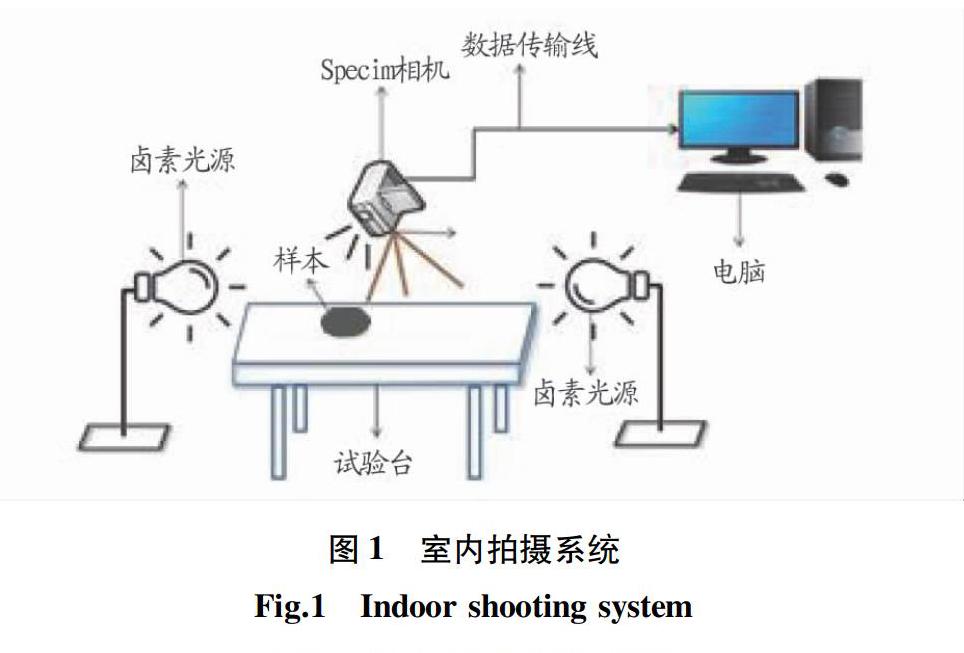
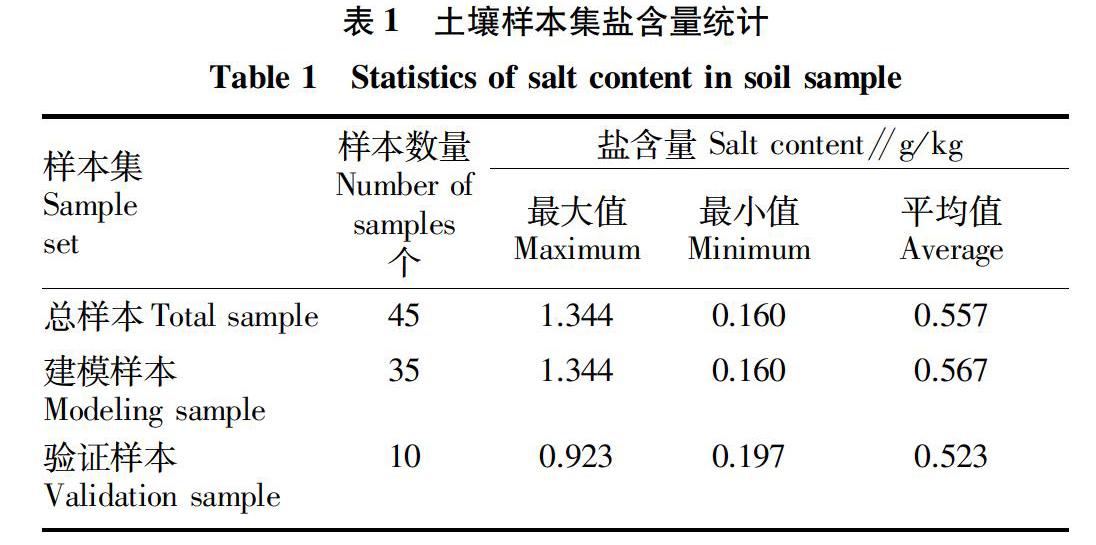
1.2 土壤样本采集与测定 样本的采集通过野外调查取样，根据该研究区耕种面积，共采集土样45份，采集土壤样本时应均匀布局采样点，采样深度为0～20 cm，将采集到的样本土壤装入密封袋内带回实验室，土壤样品过筛去除杂质，每个样本分为2份，一份利用手持式高光谱相机Specim IQ采集获得目标高光谱图像数据样本库，数据样本库的采集在实验室用室内拍摄系统（图1）拍摄获得土壤的高光谱图像，高光谱相机拍摄时，样本和白板一起拍摄，白板校正可以消除环境不匹配的问题;另一份利用HM-WSYP土壤盐分速测仪对其进行测量，HM-WSYP土壤盐分速测仪测量精度为±2%，故每份样本测量3次取其平均数作为该样本的实测盐含量。将45个样本随机分为两组，选取35个样本用于建立反演回归模型，10个样本用于模型精度的验证（表1）。

1.3 样本的光谱获取

土壤高光谱图像的获取采用高光谱相机Specim IQ获取，Specim IQ相机的波长为400～1 000 nm，光谱分辨率为3 nm，生成的高光谱图像是3D数据结构，相机始终捕获2D图像，其分辨率为512×512像素，在光谱维度上记录的光谱波段数量为204。该研究根据采集到样本图像中每个像素点的光谱曲线特征进行图像的分割及光谱的提取。不同的物体由于组成它们的分子结构不同，故它们对电磁波能量的反射、吸收、透射随波长的不同而不同。由于白板、背景和土壤的光谱反射曲线存在明显不同，根据每个像素点光谱曲线的不同进行分类，提取出土壤所有像素点的光谱曲线，并对土壤中的所有像素点的光谱反射率进行算术平均作为此样本的实际光谱曲线。

1.4 光谱预处理

高光谱图像的光谱域噪声在采集和传输等各处理环节都有可能被引入并交织呈现在高光谱图像中。常用的光谱预处理方法包括SG平滑去噪、多元散射校正、倒数、对数、微分等。其中SG平滑变换可以减少杂点，有效去除由于仪器噪声和随机误差等原因导致的高频噪声;多元散射校正可以消除土壤颗粒的不均匀，增强光谱与数据之间的相关性;倒数变换有利于显示隐藏信息，增强光谱细节，提高分辨率;微分变换可以消除其他背景干扰，提供比原始光谱更清晰的光谱轮廓变化和更高的分辨率[16-18]。针对所采集的土壤高光谱图像特性，该研究采用一阶微分（1D）、多元散射校正的一阶微分（MSC+1D）、SG平滑去噪的一阶微分（SG+1D）、对数的一阶微分（LD）对原始光谱（R）进行处理。

1.5 敏感波段的选择

由于高光谱图像的光谱波段范围广、波段窄、波段数量多，导致相邻波段之间相关性较大，高光谱图像中会存在较高的信息冗余，使得预测精度受到影响[19]。为了提取敏感波段，该研究对土壤含盐量与光谱反射率的4种变换形式进行相关性分析，并对相关系数进行α=0.01水平的显著性检验，相关系数越大表示相關性越高，此波段就越敏感。根据这一特性，选取相关系数超过显著性检验的波段为敏感波段。

1.6 偏最小二乘与随机森林模型的建立

偏最小二乘回归（PLSR）提供一种多对多线性回归建模的方法，尤其是当观测数据的样本量较少且变量之间存在多个相关性时，用偏最小二乘回归建立模型可以具有传统的经典回归分析等方法所没有的优点[20-21]，可有效简化数据结构，进而解决多个自变量之间高度线性相关的问题。

随机森林（RF）算法结构清晰、易于解释、运行效率高，对于数据要求低，且具有很好的抗噪声能力，能够处理高维度数据，不用做特征选择，训练速度快，泛化能力强，比较容易实现并行计算，不易出现过拟合问题，对于不平衡的数据来说，其还可以平衡误差[22]。在土壤盐含量的预测中，光谱的采集会受多种不确定因素的影响，有着高度的随机性和非线性，随机森林作为非参数预测模型由于不对模型的形式做假设，可以在较大的函数空间内对函数进行拟合，因而可以更好地拟合实际的模型结构，提高预测的精度。

从统计学习理论的角度分析，单个预测算法往往是基于某一类假设空间。将多个预测算法相结合，可以扩大假设空间，从而避免单个预测算法泛化性能不佳的风险，达到更高的预测精度[23]。该研究提出的偏最小二乘与随机森林的新模型（RF-PLSR、PLSR-RF）分为3个阶段： ①首先利用随机森林（或偏最小二乘）建立初始的预测模型，输入波段xi（n）（i表示样本，n表示波段）则可以得到随机森林（或偏最小二乘）在训练样本上的输出预测值y^i1，用实际值yi减去预测值y^i1得到训练残差yi2（yi2=yi-y^i1），然后输入的波段xi（n）与训练残差yi2进行组合形成新的数据集;②采用偏最小二乘（或随机森林）算法，对新的数据集进行训练，输入波段xi（n）则可以得到预测残差y^i2;③将第1阶段的预测结果y^i1与第2阶段的预测结果y^i2相加即形成最终预测结果y^i（y^i=y^i1+y^i2）。

该研究的模型即两阶段的模型相加，得到最终的预测模型。图2为算法的原理图。

1.7 模型的检验

对模型精度和质量的分析，通过计算比较模型的决定系数（R2）、均方根误差（RMSE）和相对分析误差（RPD）来进行评价。R2的取值在[0，1]区间内，R2越接近于1，表示模型的拟合效果越好;R2越接近于0，表示模型的拟合效果越差。其计算公式如下：

R2=ni=1（yi-y^i）2/ni=1（yi-y）2（1）

式中，yi为实际测量值;y^i为预测值;y为实际值的平均;n为样本数。

RMSE是用来判定模型的预测能力，RMSE越小，模型精度越高，预测能力越好，其计算公式如下：

RMSE=ni=1（yi-y^i）2/n（2）

式中，yi为实际测量值;y^i为预测值;n为样本数。

RPD应用较广，可以一定程度上减少不同研究中预测样本属性值范围差异的影响，有利于与其他相关研究对比分析。RPD越大说明所建模型越可靠，能够用于模型分析。其计算公式如下：

PRD=11-R2 （3）

式中，R2为决定系数。

该研究建模集的决定系数用Rc2表示，均方根误差用RMSEc表示，相对分析误差用RPDc表示;验证集的决定系数用Rv2表示，均方根误差用RMSEv表示，相对分析误差用RPDv表示。当决定系数R2越高、RMSE越小、RPD越大时，模型的反演准确率越高，可靠性越强，反之越低。

2 结果与分析

2.1 光谱与土壤盐含量相关性分析

土壤盐含量分别与原始光谱及其4種变换形式（1D、MSC+1D、SG+1D、LD）进行相关性分析并进行α=0.01水平的显著性检验，结果如图3所示。由图3可知，光谱进行微分变换可以使敏感波段变明显，由于土壤盐含量与原始光谱相关性较小，没有波段通过α=0.01的显著性检验，故不适合进行波段提取及建模估算;而土壤含盐量与经过1D、MSC+1D、SG+1D和LD处理后的光谱的相关性明显提高，经过1D光谱变换后敏感波段主要集中在467～549、811～854 nm，经过MSC+1D光谱变换后的敏感波段主要集中在472～549、810～863 nm，经过SG+1D光谱变换后的敏感波段主要集中在472 ～ 549、835 ～839 nm，经过LD光谱变换后的敏感波段主要集中在467 ～ 549、729 ～ 863 nm。

安徽农业科学 2021年

2.2 偏最小二乘与随机森林模型的验证

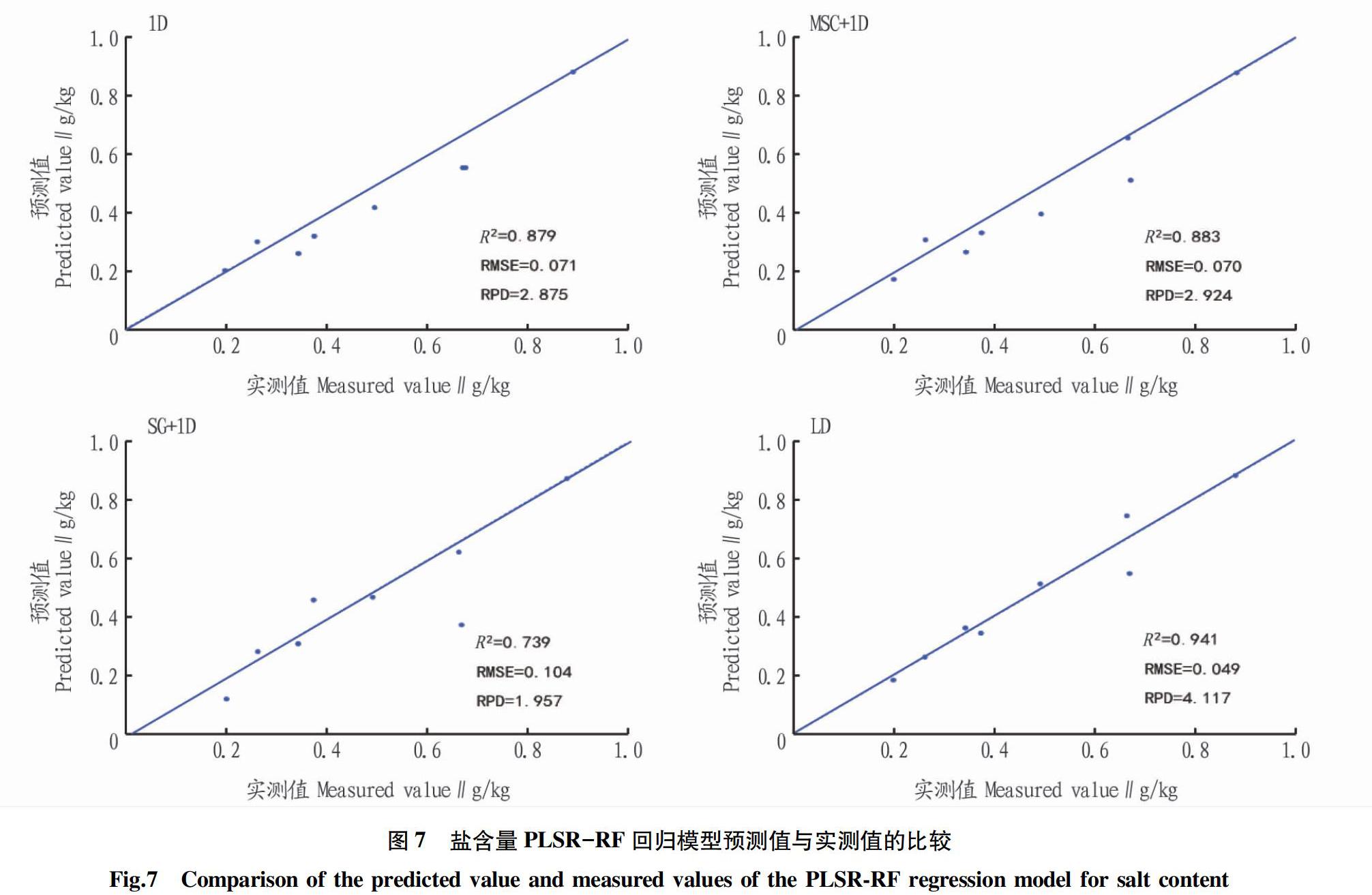
由于光谱范围的首尾部分信噪比通常较低，数据分析过程中要考虑去除首尾部分，即400～450和900～1 000 nm的光谱。为了用采集到的土壤高光谱图像对土壤实际含盐量进行预测，该研究中所有回归模型的自变量为选取相关系数由高到低的前10个敏感波段，因变量为样本土壤的盐分实测含量。PLSR回归模型、RF回归模型、RF-PLSR回归模型和PLSR-RF回归模型的检验结果如表2所示。通过表2可以发现，偏最小二乘（PLSR）建模集的决定系数Rc2相对偏低，均方根误差RMSEc相对偏大，相对分析误差RPDc没有超过1.4，证明模型的拟合度和可靠性较差，预测精度较低。建立的RF-PLSR回归模型和PLSR-RF回归模型与PLSR和RF回归模型相比，发现2种模型结合后建模集的决定系数Rc2有所提高，均方根误差RMSEc有所降低，相对分析误差RPDc都超过2.0。其中最优模型为光谱经过对数的一阶微分变换建立的PLSR-RF反演模型，其建模集决定系数Rc2为0.852，均方根

误差RMSEc为0.102 g/kg，相对分析误差RPDc为2.600，验证集决定系数Rv2为0.941，均方根误差RMSEv为0.049 g/kg，相对分析误差RPDv为4.117。

从盐含量与PLSR、RF、RF-PLSR、PLSR-RF回归模型预测值与实测值的比较（图4～7）可以看出，PLSR和RF回归预测模型的验证集中有些样本偏离1∶1线较为严重，而RF-PLSR、PLSR-RF回归预测模型验样本基本在1∶1线附近。说明将2个预测算法相结合可以提高预测精度。

从研究结果来看，原始光谱的反射率经过光谱变换后与实测含盐量的相关性有明显的提高，可以更好地突出敏感波段，建立的4种回归反演模型中新提出的RF-PLSR和PLSR-RF回归模型相比PLSR和RF回归模型决定系数提高、均方根误差降低、相对分析误差变高，证明模型的拟合效果提高，精度变高，可靠性变强，可以更好地反演土壤含盐量。而通过LD光谱变换所建立的PLSR-RF回归模型拟合效果最好，且预测精度最高，其建模集决定系数Rc2为0.852，均方根误差RMSEc为0.102 g/kg，相对分析误差RPDc为2.600，验证集决定系数Rv2为0.941，均方根误差RMSEv为0.049 g/kg，相对分析误差RPDv为4.117。由此可见，PLSR-RF回归模型为今后预测土盐含量提供了一个新的思路。

通过表2中各预测方法的结果可知，该研究提出的偏最小二乘与随机森林结合的预测方法取得了较高的预测精度，原因是采用了残差学习，如果使用偏最小二乘与随机森林单独建模预测则可能会导致训练数据中某些相关信息缺失，从统计学习理论的角度分析，采用2种模型预测可以扩大模型的假设空间，尽可能地使假设空间包含数据之间的真实关系，而通过残差学习对各个模型进行组合，可以扩大预测模型的假设空间，进而在更大的假设空间内对数据之间的真实关系进行搜索，提高了模型对数据之间真实关系的逼近能力，从而提高模型的预测精度。在预测土壤盐含量的研究中，该研究首次提出的2种模型的结合，与现有的高光谱反演土壤盐含量的研究相比，2种模型的结合可以提高反演土壤盐含量的精确度，为指导农田提供参考。

3 结论

该研究结果表明，土默川平原土壤高光谱反射率进行光谱变换可以更好地突出敏感波段;而采用对残差进行学习的2种模型的结合可以提高泛化能力和反演精度，模型的可靠性也提高。该研究提出的2种模型相结合不仅为研究土壤盐含量提供了参考价值，同时也为今后研究土壤其他成分含量提供了一个新的思路。

参考文献

[1]刘全明，成秋明，王学，等.河套灌区土壤盐渍化微波雷达反演[J].农业工程学报，2016，32（16）：109-114.

[2]郝远远，徐旭，任东阳，等.河套灌区土壤水盐和作物生长的HYDRUS-EPIC模型分布式模拟[J].农业工程学报，2015，31（11）：110-116，315.

[3]吴亚坤，刘广明，苏里坦，等.多源数据的区域土壤盐渍化精确评估[J].光谱学与光谱分析，2018，38（11）：3528-3533.

[4]王涛，喻彩丽，姚娜，等. MLR和PLSR的沙壤土盐分含量光谱检测对比研究[J].干旱区地理，2018，41（6）：1295-1302.

[5]张俊华，贾萍萍，孙媛，等.基于高光谱特征的盐渍化土壤不同土层盐分离子含量预测[J].农业工程学报，2019，35（12）：106-115.

[6]陶培峰，王建华，李志忠，等.基于高光谱的土壤养分含量反演模型研究[J].地质与资源，2020，29（1）：68-75，84.

[7]王丹阳，陈红艳，王桂峰，等.无人机多光谱反演黄河口重度盐渍土盐分的研究[J].中国农业科学，2019，52（10）：1698-1709.

[8]张雅莉，塔西甫拉提·特依拜，阿尔达克·克里木，等. 基于Landsat8 OLI影像光谱的土壤盐分估算模型研究[J].国土资源遥感 2018，30（1）：87-94.

[9]FARIFTEH J，VAN DER MEER F，CARRANZA E J M. Similarity measures for spectral discrimination of salt-affected soils[J]. International journal of remote sensing，2007，28（23）：5273-5293.

[10]SRIVASTAVA R，SETHI M，YADAV R K，et al. Visible-near infrared reflectance spectroscopy for rapid characterization of salt-affected soil in the indo-gangetic plains of Haryana，India[J]. Journal of the Indian society of remote sensing，2017，45（2）：307-315.

[11]张智韬，魏广飞，姚志华，等.基于无人机多光谱遥感的土壤含盐量反演模型研究[J].农业机械学报，2019，50（12）：151-160.

[12]陈俊英，姚志华，张智韬，等.大田葵花土壤含盐量无人机遥感反演研究[J].农业机械学报， 2020，51（7）：178-191.

[13]马利芳，熊黑钢，张芳.基于野外 VIS-NIR 光谱的土壤盐分主要离子预测[J].土壤，2020，52（1）：188-194.

[14]张贤龙，张飞，张海威，等.基于光谱变换的高光谱指数土壤盐分反演模型优选[J].农业工程学报，2018，34（1）：110-117.

[15]马驰.基于HJ-1A高光谱影像的土壤盐碱化遥感研究[J].干旱区资源與环境，2014，28（2）：180-184.

[16]石朴杰，王世东，张合兵，等.基于高光谱的复垦农田土壤有机质含量估测[J].土壤，2018，50（3）：558-565.

[17]于雷，洪永胜，耿雷，等.基于偏最小二乘回归的土壤有机质含量高光谱估算[J].农业工程学报，2015，31（14）：103-109.

[18]褚小立，袁洪福，陆婉珍.近红外分析中光谱预处理及波长选择方法进展与应用[J].化学进展，2004，16（4）：528-542.

[19]张号逵，李映，姜晔楠.深度学习在高光谱图像分类领域的研究现状与展望[J].自动化学报，2018，44（6）：961-977.

[20]蒋烨林，王让会，李焱，等.艾比湖流域不同土地覆盖类型土壤养分高光谱反演模型研究[J].中国生态农业学报，2016，24（11）：1555-1564.

[21]高惠璇.两个多重相关变量组的统计分析（3）（偏最小二乘回归与PLS过程）[J].数理统计与管理，2002，21（2）：58-64.

[22]贾文超，戚兰兰，施凡，等.采用随机森林改进算法的WebShell检测方法[J].计算机应用研究，2018，35（5）：1558-1561.

[23]ZHOU Z H. Ensemble methods：Foundations and algorithms[M].Boca Raton，USA：CRC Press，2012.