黏土压密注浆补偿效率评估方法研究

蒋功化，向洲辰

黏土压密注浆补偿效率评估方法研究

蒋功化1，向洲辰2

(1. 湖南路桥建设集团有限责任公司，湖南 长沙 410004；2. 中南大学 土木工程学院，湖南 长沙 410075)

针对新建常德经益阳至长沙铁路站前工程，从注浆补偿效率损失机理出发，基于太沙基一维固结理论，对该工程黏土段压密注浆补偿效率进行研究。首先，以浆泡为界将黏土层分为上下两部分。而后，基于太沙基一维固结理论，对黏土层上下两层分别进行积分计算求得其固结沉降体积量，进而计算黏土压密注浆补偿效率值。利用现有文献的试验数据对本文所提出方法进行验证。最后，分析并讨论基于新建常德经益阳至长沙铁路站前工程注浆参数下注浆压力对注浆补偿效率的影响。研究结果表明：注浆补偿效率随着时间先减小而后在=1 000 s后维持稳定，且注浆压力与注浆补偿效率的最终值成反比。所得结果可用于新建常德经益阳至长沙铁路站前工程黏土段溶洞注浆工程的设计和施工。

太沙基一维固结理论；黏土；固结沉降；注浆补偿效率

在黏土中采用压密注浆方式来补偿地表沉降时，由于黏土透水性差，浆料中的水很难从浆料中转移至土体，因此黏土中采用压密注浆方式的补偿效率不会像砂土一样迅速降低并保持稳定。此外，在注浆完成后的一段时间内，黏土固结作用会产生固结沉降，导致地表下陷，进而会导致其补偿效率降低。目前对于黏土中采用压密注浆的研究基本都是基于试验或是数值模拟的方法[1−10]。Au 等[3]研究了黏土中补偿灌浆效率的影响因素，将试验结果与数值模拟结果进行了对比，证明了注浆效率将会随着时间显著降低，同时也发现注浆效率会随着土体超固结比OCR的增加和浆料水灰比/的降低而增加。Soga等[7]通过试验观察到在正常固结黏土中，在注浆完成时，补偿灌浆效率为80%～90%，但在随后很长一段时间内将持续降低。理论方法多针对砂土条件下注浆研究[5]，而很少有涉及黏土条件下注浆的理论研究，本文拟填补这一研究空白。针对新建常德经益阳至长沙铁路站前工程，本文基于太沙基一维固结理论，提出适用于该工程黏土段注浆效率求解模型。模型以浆泡为界将黏土层分为上下两部分，分别对上下两层进行固结沉降分析，并进行积分计算求得其固结沉降体积量，进而计算补偿效率值。利用Soga等[7]的试验数据对本文所提出方法进行验证，验证结果说明了本文所提出理论模型能够准确地对黏土注浆补偿效率进行评估。随后分析并讨论基于新建常德经益阳至长沙铁路站前工程注浆参数下注浆压力对注浆补偿效率的影响。

1 黏土中的注浆补偿效率损失分析

Soga等[7]总结了注浆浆料体体积损失的过程，主要包括以下3种情况：

1) 浆料的渗透效应导致的注浆体积损失：在注浆压力的作用下，浆液中的水会渗透进入土体中，导致浆料体的最终体积V小于浆料的注入体 积V；

2) 土体固结效应导致的注浆体积损失：浆料周围的土体会因为注浆压力在注浆过程中以及注浆结束之后，由于超孔隙水压力的消散而发生土体固结，进而导致固结的土体周围的体积变化量V小于浆料体的最终体积V；

3) 几何效应导致的注浆体积损失：压密或固结的土体周围的体积变化量V不会全部用来补偿地表沉降，部分会导致地下结构物的位移，例如隧道衬砌的位移，这会使得地表的抬升体积量V小于压密或固结的土体周围的体积变化量V。

因此，压密注浆补偿效率可以看成由以下三部分组成：浆料的渗透效应(η=V/V)；土体的压密/固结效应(η=V/V)；几何效应(η=V/V)。因此，压密注浆补偿效率的损失率可表示为：

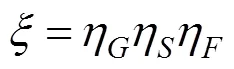
对于黏土，由于其渗透性差，在注浆过程中往往忽略浆液在黏土中的渗透作用η=0。当忽略注浆对地下结构物的几何效应时η=0，则黏土中压密注浆补偿效率的损失率可表示为：

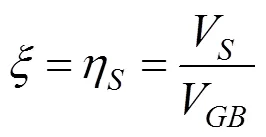
由于不考虑黏土渗透作用，浆料中的水难以从浆料中转移到周围土体中，因此土体中的浆料体积V和浆料的注入体积V相等，则式(2)也可改 写为：

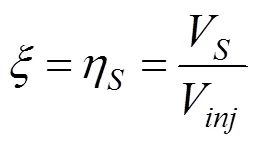
所以，黏土中的注浆补偿效率损失，主要由注浆引起的土体固结压密而产生，故可通过计算注浆引起的地表固结沉降体积V进而得到注浆抬升地表的体积差，进而计算补偿效率，见下式：

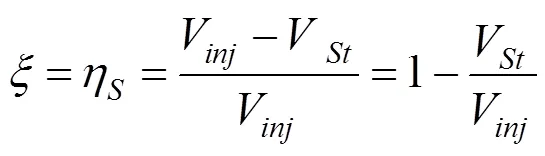
2 太沙基一维固结理论

2.1 基本假定

太沙基基于侧限固结试验模型，用弹簧模拟土体骨架，提出了太沙基一维固结理论[8]。太沙基固结理论作为土体固结问题研究的基础理论，自提出以来得到了广泛应用[11−12]。太沙基固结理基本假定如下：

1) 土体是饱和的均质线弹性体；

2) 土体固结变形是微小的；

3) 土颗粒和孔隙水不可压缩；

4) 土体中的渗流服从达西定律；

5) 土中渗流和变形仅发生在荷载作用的方 向上；

6) 在固结过程中，土体的压缩性和压缩性均保持不变；

7) 外加荷载连续分布且一次性瞬时施加。

黏土性质满足以上假定，因此可应用太沙基固结理论对黏土压密注浆补偿效率的损失率进行 计算。

2.2 太沙基一维固结方程

太沙基一维固结方程可表示为式(5)～(6)：

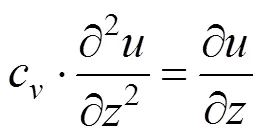
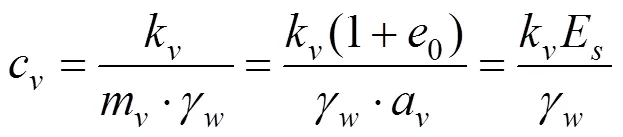
式中：表示任一时刻，任一深度的孔隙水压力；C表示固结系数；k表示土的渗透系数；E表示土的压缩模量；γ表示水的重度；m表示土的体积压缩系数，其大小等于a/(1+e)；a表示土的压缩系数；0表示土的初始孔隙比。

自太沙基一维固结理论提出后，还相继提出了不少二维、三维的固结理论。但由于二维、三维固结理论计算的复杂性，太沙基一维固结理论一直都是研究土体固结和计算固结沉降的主要手段。此外，考虑到在黏土中注浆，孔隙水往往只可能从黏土层的上顶面和下底面排出，因此本文选择用太沙基一维固结理论来研究黏土压密注浆补偿效率。

3 黏土压密注浆补偿效率计算

3.1 基本假定

为便于计算，在太沙基一维固结理论假定的基础上，进行以下假定：

1) 土体为正常固结土，即超固结比=1；

2) 由于注浆过程相对于固结过程而言时间往往很短，故可忽略注浆过程中的固结作用，即假定浆料是在土体中以注浆压力p瞬时注入的，浆泡瞬间形成并结束注浆，固结随即开始；

3) 假定土体固结主要发生在由于注浆引起的被抬升的范围内，范围以外的固结效应忽略不计；

4) 以浆料体中心点(即注浆点)所在的水平面为分界面，假定分界面以上的孔隙水从上顶面排出，分界面以下的孔隙水从下底面排出；

5) 由于分界面以上的土体会被抬升，故可假定分界面以上的初始孔隙水压力为上覆层荷载，而分界面以下的初始孔隙水压力则由注浆压力提供；

6) 在分界面以下，由于初始孔隙水压力由注浆压力提供，而注浆压力的方向为径向，可以等效地认为土体中以浆泡中心点为原点的初始径向孔隙水压力大小均为p，则任一径向上，孔隙水压力都可分解为水平方向和竖直方向，面上每一个点不同深度Z处的竖直方向的初始孔隙水压力则与注浆压力p和深度有关(见图1)；

7) 孔隙水只会从黏土层的上顶面和下底面排出，故可假定只考虑竖直方向的渗流和固结变形。

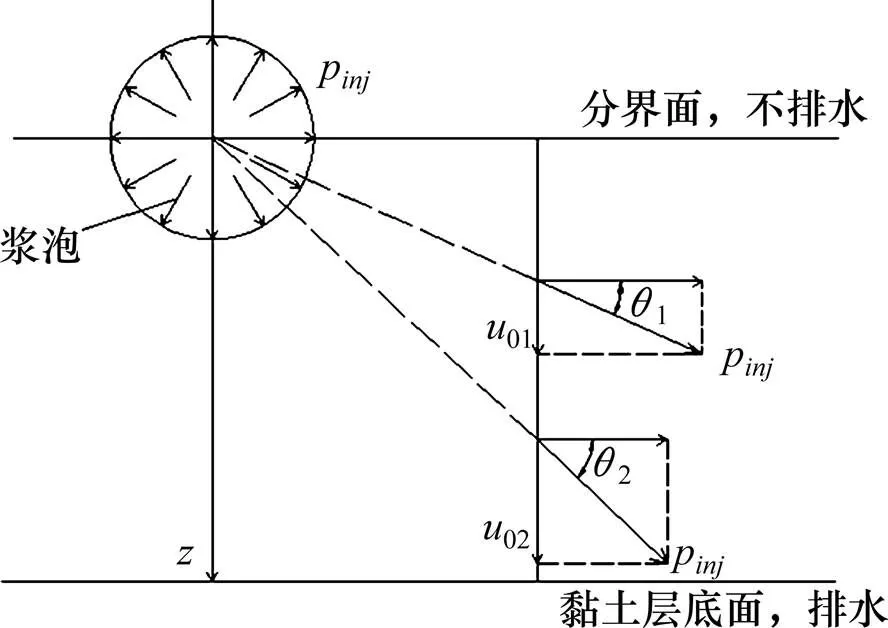
图1 浆泡以下土层的初始孔隙水压力与注浆压力的关系示意图

3.2 固结沉降量计算

3.2.1 分界面以下土体固结沉降量计算

建立空间直角坐标系，为方便计算，轴正向为竖直向下，原点为浆料中心。设分界面以下黏土层的厚度为1。

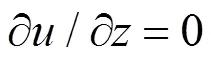
根据式(5)，可采用分离变量法求解孔隙水压力(,)的表达式，表示如下：

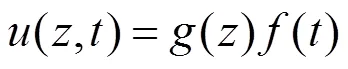
将式(7)代入式(5)可得

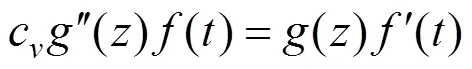
假定下式：

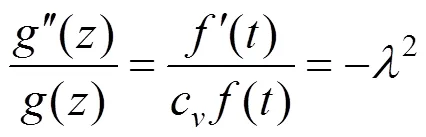
结合式(9)可得：

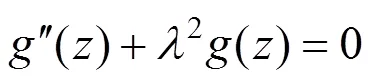
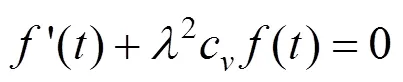
式(11)为二阶常系数齐次线性微分方程，其通解可表示为：

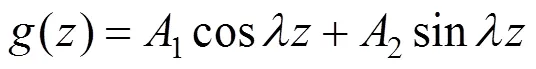
代入边界条件，可得：

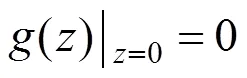
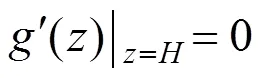
可得：

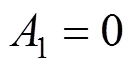
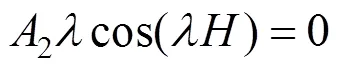
可得：

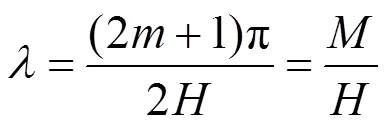
式中：

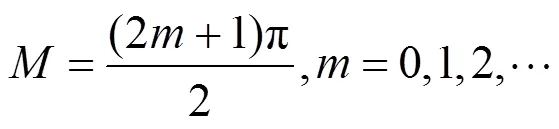
可得：

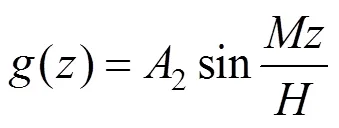
式(10)为一阶线性微分方程，其通解可表示为：

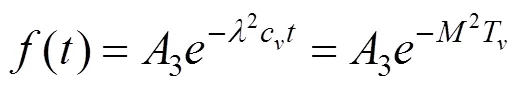
其中

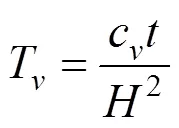
则由

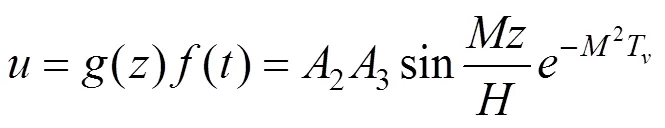
将所有的解叠加，可得：

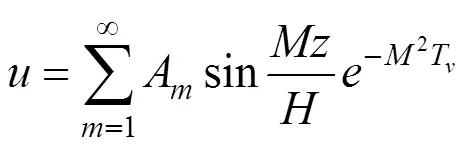
代入边界条件，可得：

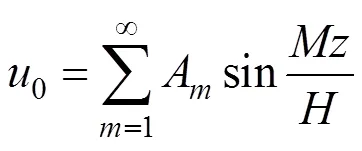
可得：

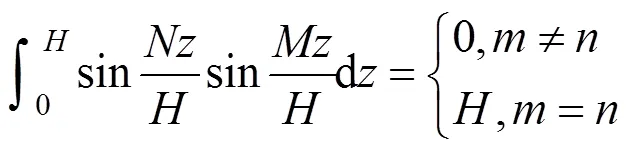
因为

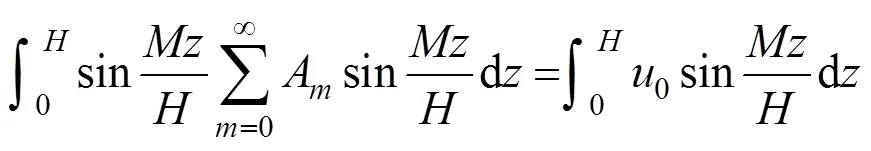
则可得：

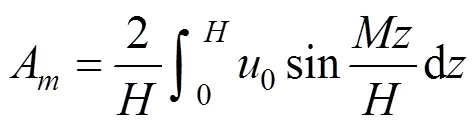
由3.1的基本假定可知，任一点()的初始孔压为：

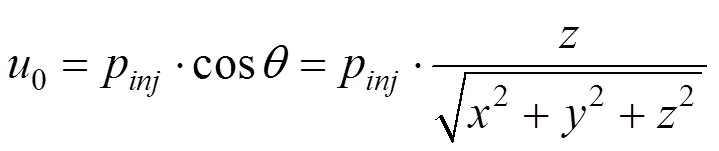
代入式(26)可得：

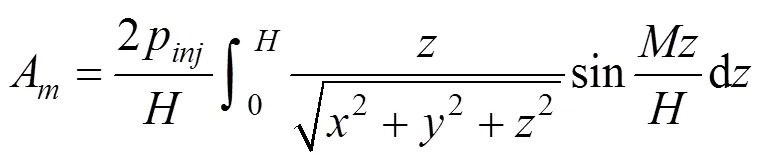
所以，任一时刻，任一点()处的沉降可计算得：

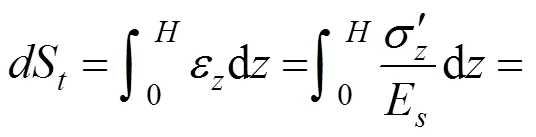
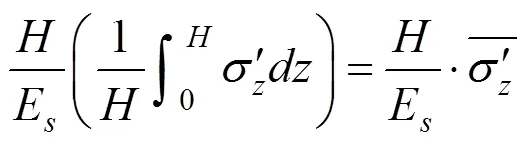
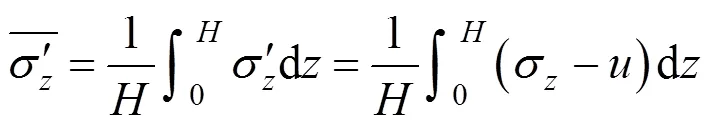
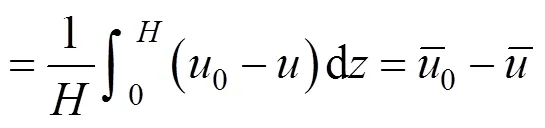
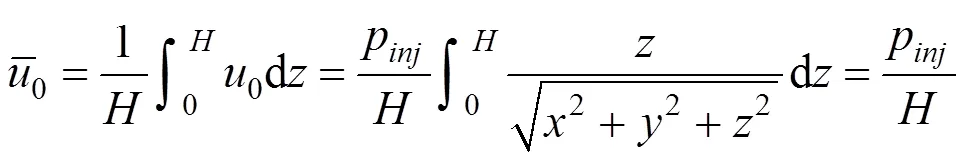
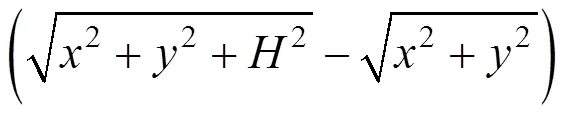
因为

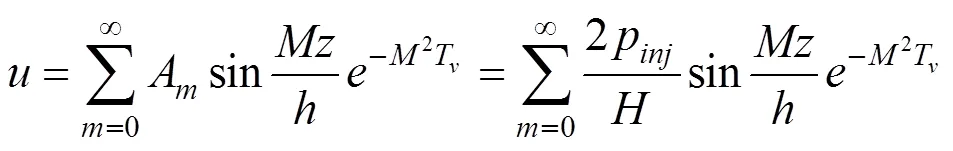
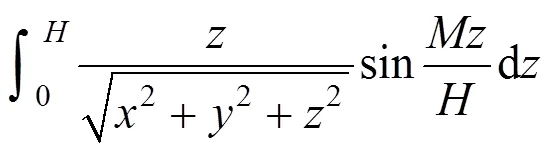
则面上任一点任一时刻全土层厚度1的平均孔压为：

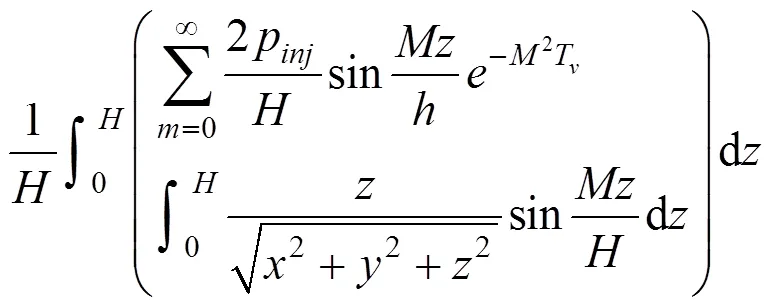
故任一时刻，地表任一点的沉降量可表示为：

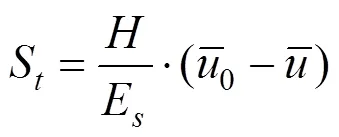
将整个沉降范围划分为无数个微小柱体，积分可得整个区域内任一时刻固结沉降体积量为：

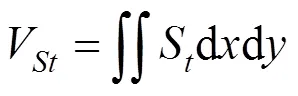
由于假定固结沉降只发生在地表被抬升范围内，则上式的积分范围为以0为半径的圆面，代入可得任一时刻的分界面以下土体固结沉降体积 量V1：

式中：0表示压密注浆锥形剪切破坏模型下的地表抬升范围圆形半径。

3.2.2 分界面以上土体固结沉降量计算

建立空间直角坐标系，若以浆料中心为原点，轴正向为竖直向上，原点为浆料中心。设分界面以下黏土层的厚度为2。

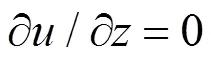
故此时固结方程的解和分界面以下是相同的，区别仅在于初始孔隙水压力值不同。此时的初始孔隙水压力为上覆土层荷载p，可表示为：

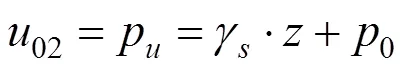
其中，γ表示黏土重度；0表示初始外加荷载。

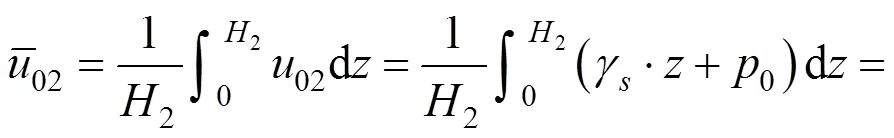
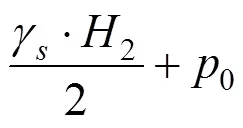
因为

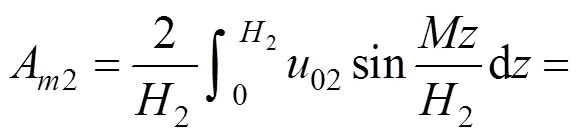
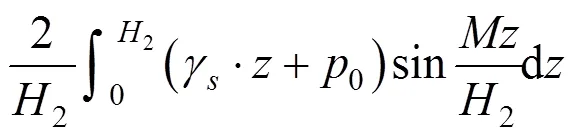
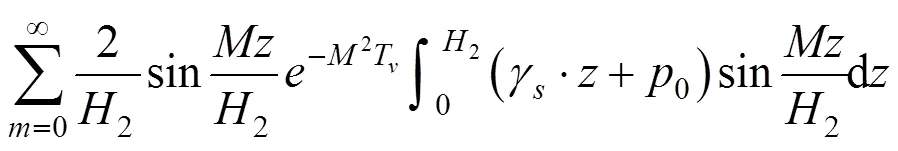
所以面上任一点任一时刻全土层厚度2的平均孔压可表示为：

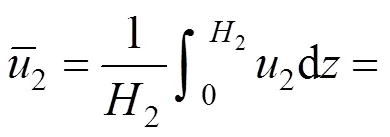
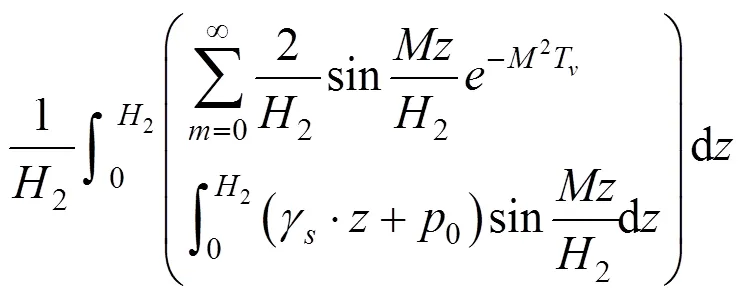
因此同理可得分界面以上土体固结沉降体积量V12：

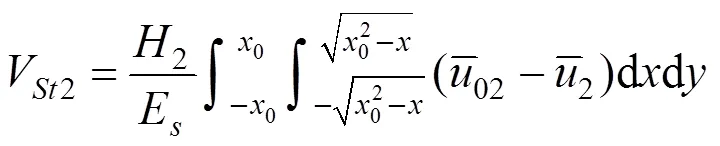
3.3 补偿效率计算

则结合式(4)可得注浆补偿效率值为：

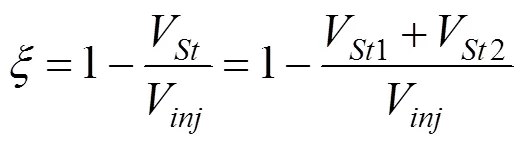
4 对比验证

本文所提出方法计算结果与Soga等[7]固结实验结果对比进而验证本文所提出方法的准确性。Soga等[7]固结实验所采用的的参数见表1。比较结果如图2所示。

表1 Soga等固结试验参数

图2 本文所提出模型与Soga等实验的结果对比

由图2可知，Soga等[7]的实验中所测得的初始注浆补偿效率会略低于1，约为0.88，这是由于实验中注浆管里本身会存留空气，在压入浆料时会被压缩。同时由图2可知，本文所提出模型计算所得结果与Soga等[7]的实验结果在注浆补偿效率变化趋势、变化速率上一致。此外，从图2中也可看出，本文所提出的模型计算所得的补偿效率比实验结果略微偏高，平均误差小于12%。因此可认为该计算模型的结果与试验结果相符合，模型具有有效性和合理性。

5 参数分析

将本文所提出的方法对基于新建的常德经益阳至长沙铁路站前工程注浆参数下注浆压力对注浆补偿效率进行分析并讨论。图3所示为新建的常德经益阳至长沙铁路站前工程注浆孔布置示意图，由图3可知，注浆孔布置采用正方形布置，孔间距5 m。注浆水泥采用P042.5水泥，水泥浆液水灰比为0.8:1-1:1。讨论注浆压力在20～30 kPa情况下，时间和注浆压力对注浆补偿效率的影响，计算结果见图4。

由图4可知，注浆压力随着时间先迅速减小而后保持稳定。注浆压力p与注浆补偿效率的最终值成反比，较大的p会产生较大固结沉降，进而导致降低以上所得结果可用于指导新建的常德经益阳至长沙铁路站前工程黏土段溶洞注浆工程的设计和施工。

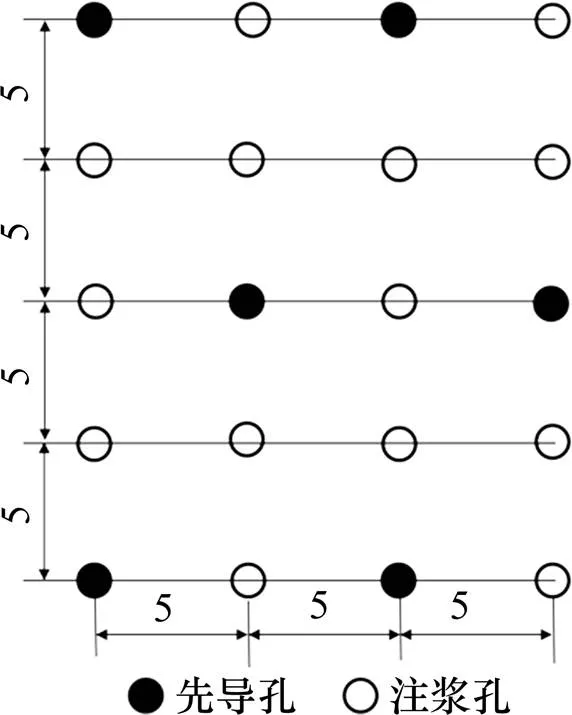
图3 注浆孔布置示意图

图4 注浆压力pinj对注浆补偿效率的影响

6 结论

1) 通过与Soga等固结实验结果对比，验证了本文所提出计算模型的有效性和合理性。

2) 参数分析结果表明注浆补偿效率随着时间先减小而后在=1 000 s后维持稳定，且注浆压力与注浆补偿效率的最终值成反比。所得结果可用于指导新建的常德经益阳至长沙铁路站前工程黏土段溶洞注浆工程的设计和施工。

[1] 刘奇, 陈卫忠, 袁敬强, 等. 岩溶充填黏土注浆加固试验研究[J]. 岩石力学与工程学报, 2019(增1): 3179− 3188. LİU Qi, CHEN Weizhong, YUAN Jingqiang, et al. Laboratory experiment study of grouted materials filled in karst caverns[J]. Chinese Journal of Rock Mechanics and Engineering, 2019(Suppl1): 3179−3188.

[2] 吴悦, 赵春风, 王有宝, 等. 黏土中考虑土体卸荷效应的后注浆压密模型[J]. 哈尔滨工业大学学报, 2020, 52(11): 1−7. WU Yue, ZHAO Chunfeng, WANG Youbao, et al. Compaction grouting model in clay considering unloading effect[J]. Compaction Grouting Model in Clay Considering Unloading Effect, 2020, 52(11): 1−7.

[3] Au S K A, Soga K, Jafari M R, et al. Factors affecting long-term efficiency of compensation grouting in clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(3): 254−262.

[4] LI Liang, XIANG Zhouchen, ZOU Jinfeng, et al. An improved model of compaction grouting considering three-dimensional shearing failure and its engineering application[J]. Geomechanics and Engineering, 2019, 19(3): 217−227.

[5] XU Xianghua, XIANG Zhouchen, ZOU Jinfeng, et al. An improved approach to evaluate the compaction compensation grouting efficiency in sandy soils[J]. Geomechanics and Engineering, 2020, 20(4): 313−322.

[6] Bolton M D, Soga K, Jafari M R, et al. Soil consolidation associated with grouting during shield tunnelling in soft clayey ground[J]. Géotechnique, 2001, 51(10): 835−846.

[7] Soga K, Au S K A, Jafari M R, et al. Laboratory investigation of multiple grout injections into clay[J]. Géotechnique, 2004, 54(2): 81−90.

[8] 王丽军, 赵利明, 朱光翠. 采用分离变量法求解太沙基一维固结微分方程[J]. 公路, 2019, 64(2): 88−91. WANG Lijun, ZHAO Liming, ZHU Guangcui. Study on the One dimensional consolidation differential equation of Terzaghi by the separation of variables method[J]. Road, 2019, 64(2): 88−91.

[9] Shrivastava N, Zen K. Finite element modeling of compaction grouting on its densification and confining aspects[J]. Geotechnical and Geological Engineering, 2018, 36(4): 2365−2378.

[10] Krok A, WU C Y. Finite element modeling of powder compaction[M]// Engineering Crystallography: From Molecule to Crystal to Functional Form. Springer, Dordrecht, 2017: 451−462.

[11] 士贺飞. 反复荷载作用下软土固结变形研究[D]. 郑州: 河南工业大学, 2019. SHI Hefei. Experimental study on consolidation deformation of soft soil under repeated loading[D]. Zhengzhou: Henan University of Technology, 2019.

[12] 马青山, 贾军元, 田福金, 等. 地下水开采引发的土体变形对污染物迁移影响研究[J]. 中国煤炭地质, 2019, 31(2): 35−40. MA Qingshan, JIA Junyuan, TIAN Fujin, et al. Study on ımpact from soil mass deformation on pollutant migration ınitiated by groundwater exploitation[J]. Coal Geology of Chına, 2019, 31(2): 35−40.

Research on the estimation method of compensation efficiency of clay compaction grouting

JIANG Gonghua1, XIANG Zhouchen2

(1. Hunan Road & Bridge Co., Ltd., Changsha 410004, China;2. School of Civil Engineering, Central South University, Changsha 410075, China)

For the new Changde railway station from Yiyang to Changsha, based on the mechanism of grouting compensation efficiency loss and Terzaghi’s one-dimensional consolidation theory, the grouting compensation efficiency in clay is studied in this paper. Firstly, the clay layer was divided into two parts with the slurry bubble as the boundary, namely the upper part and the lower part. Then, based on Terzaghi’s one-dimensional consolidation theory, the consolidation settlement of the upper and lower layers was calculated by integral calculation respectively, and then the grouting compensation efficiency was calculated. The proposed method was verified by the experimental data of existing work. Finally, the influence of the grouting pressure on the grouting compensation efficiency is analyzed and discussed based on the grouting parameters of the New Changde railway station from Yiyang to Changsha. The results show that the grouting compensation efficiency first decreases with time, and then remains stable after=1 000 s, and the grouting pressure is inversely proportional to the final value of the grouting compensation efficiency. These results can be used for the design and construction of the karst cave grouting in the clay section of the New Changde railway station from Yiyang to Changsha.

Terzaghi’s one-dimensional consolidation theory; clay; consolidation settlement; grouting compensation efficiency

10.19713/j.cnki.43−1423/u.T20200991

U45

A

1672 − 7029(2021)04 − 0942 − 07

2020−10−22

贵州省科技重大专项资助项目(黔科合重大专项[2018]3010)

蒋功化(1979−)，男，湖南常德人，高级工程师，从事交通土建工程建设；E−mail：1023618780@qq.com

(编辑 蒋学东)