基于改进和声算法的TSP路径求解*

吴 莹，欧 云，姚玄石，丁 雷

(吉首大学信息科学与工程学院，湖南 吉首 416000)

1 研究背景

旅行商问题(Traveling Salesman Problem， TSP)是一个具有广泛应用背景和重要理论意义的组合优化问题，它可以描述为[1]：给定一个城市的集合，寻找一条从某城市出发，然后遍历其他各个城市，且每个城市能且仅能经过1次，最后回到出发城市的最短路径.TSP的数学模型描述如下：

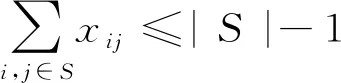
xij∈{0,1}i,j=1,…,n.

其中：P为给定城市的集合，P={1,2,…,n}；dij为城市i与城市j之间的距离，距离集合D={dij}；n为城市个数.TSP的目标函数是求得经过集合中所有城市的最短路径，约束条件是不重复经过同一城市且最终回到出发城市.

TSP是一个求解最短路径的经典NP-Hard问题[2]，目前没有统一的解法.近年来，以粒子群算法、遗传算法(Genetic Algorithm， GA)、蚁群算法为代表的群智能算法，因采用分布式计算和基于概率搜索，且具有鲁棒性较强和实现简单等特点，被广泛运用在TSP求解中.乔彦平等[1]将GA与模拟退火算法(Simulated Annealing Algorithm， SAA)相结合，改善了TSP的求解精度；陶丽华等[3]将GA与蚁群算法进行动态融合，一定程度上提高了TSP的求解精度和速度.作为现有群智能算法之一，和声搜索算法(Harmony Search Algorithm， HSA)因其原理简单、可调参数少和容易实现等优势，在函数参数优化[4]、图形图像分割[5]、最优路径[6]和背包问题[7]中得到很好的应用.但由于受到搜索范围和和声记忆库(Harmony Memory， HM)种群多样性的限制，HSA存在早熟和收敛精度低等问题，因此众多研究者对其进行了改进.如高立群等[8]提出了一种提高初始解质量的改进HSA；杨树欣等[9]从优化迭代过程方面改进了HSA；张康丽等[10]结合GA的概率分配方法，对HM的种群信息的多样性作了改进.为了进一步提高HSA的收敛速度和准确度，针对算法中音调调节概率设置为固定值而导致HM多样性受限、易于陷入局部搜索等不足，笔者拟设计一个动态调节音调概率的新算法，即动态和声搜索算法(Dynamic Harmony Search Algorithm， DHSA)，并将其运用到TSP求解中，以期实现遍历路径最优化.

2 算法原理

2.1 HSA原理

HSA[11]与粒子群算法[12]来源于鸟类捕食的思想类似，HSA是仿照音乐表演过程，将创作美妙和声的过程类比为寻求最优解的过程，本质上是一种优化设计的过程.HAS中，乐器i(i=1，2，…，m)相当于优化问题中的第i个设计变量，各乐器声调的和声Xj(j=1，2，…，M)相当于优化问题的第j个解向量，评价和声的好坏相当于评价目标函数f(Xj)解的优劣.HAS思想是：首先产生SHMS个初始解存入HM内，以选择概率PHMCR在HM内搜索新解，以概率1-PHMCR在HM外的变量值域中搜索；然后以音调调节概率PPAR和调节步长Bw对新解产生局部扰动；最后判断新解是否优于HM内的最差解，若是，则替换之，不断迭代，直至达到最大迭代次数T为止.

2.2 DHSA原理

HSA中，音调调节概率和调节步长这2个控制参数在迭代求解过程中是固定不变的，因此算法在搜索过程中无法随着搜索范围的变化做出相应调整，容易陷入局部最优，限制HM的多样性，从而算法的求解效率较低.目前，对HSA性能的改进，主要是从修改算法参数、设计合适算子和融合其他智能算法3个方面进行的.笔者拟从调整算法参数入手，先动态调节音调概率参数，以保障HM种群信息的多样性，避免陷入局部搜索；再对HM的存储结构和新和声的产生方式作改进，采用禁忌表存储及轮盘赌选择方法来提高搜索效率.动态调节音调概率参数公式为

PPAR=PPARmin+(PPARmax-PPARmin)t/T.

(1)

其中：PPARmin，PPARmax分别为和声音调调节概率的最小值和最大值；t为当前迭代次数；T为最大迭代次数.

DHSA和HSA的参数对比结果列于表1.

3 DHSA在TSP求解中的应用

在利用DHSA求解TSP时，将TSP路径库表示为HM，2个城市之间的路径表示为一个乐器的和音，TSP的一个解(连接所有城市的一条无重复且形成回路的访问路径)表示为由不同乐器的和音形成的一段和声.TSP路径库表示为

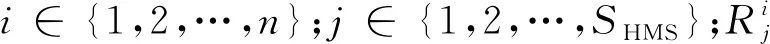
DHSA的基本步骤如下：

(ⅰ)导入城市坐标，初始化参数，初始化TSP路径库.

(ⅱ)遍历每个城市，采用禁忌表约束TSP路径库，使每个城市出现次数都唯一.

图1 DHSA流程Fig. 1 Flowchart of DHSA

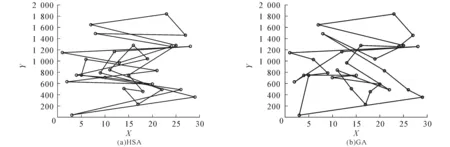
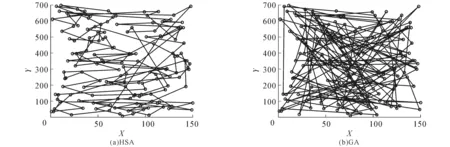
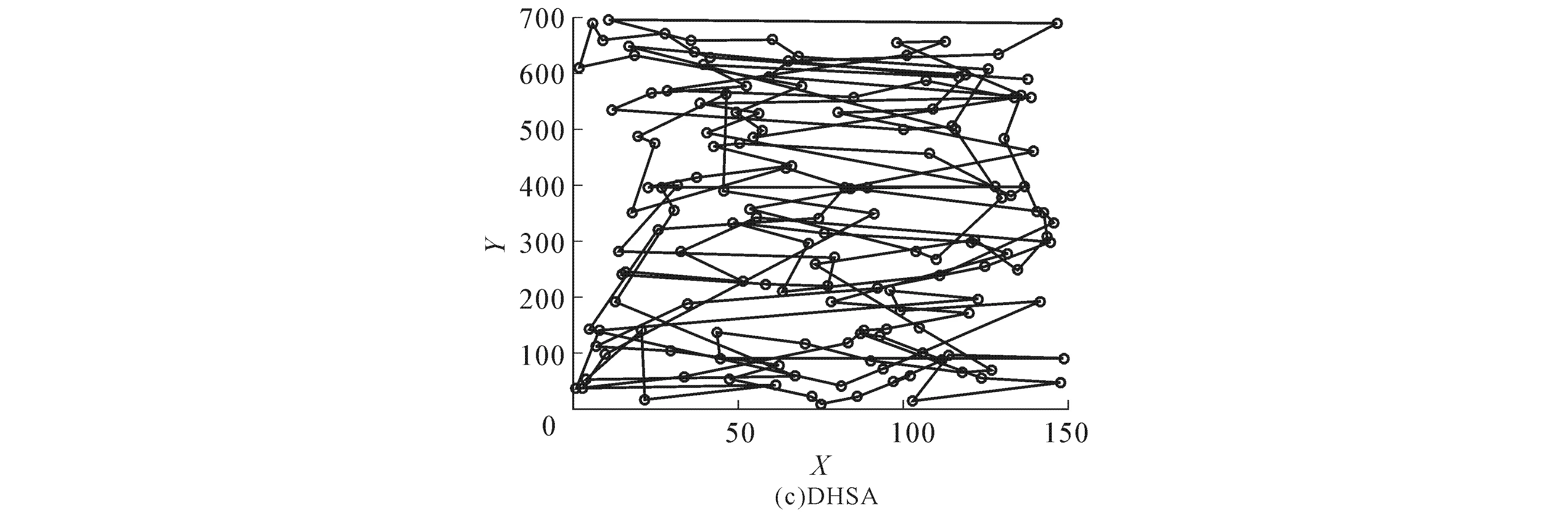
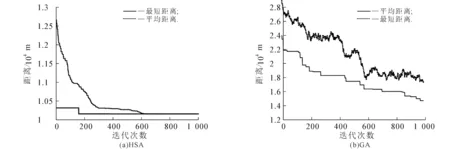
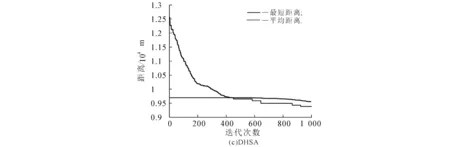
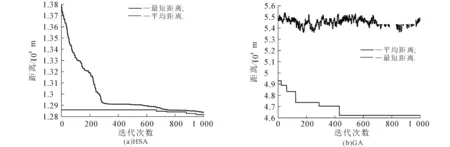
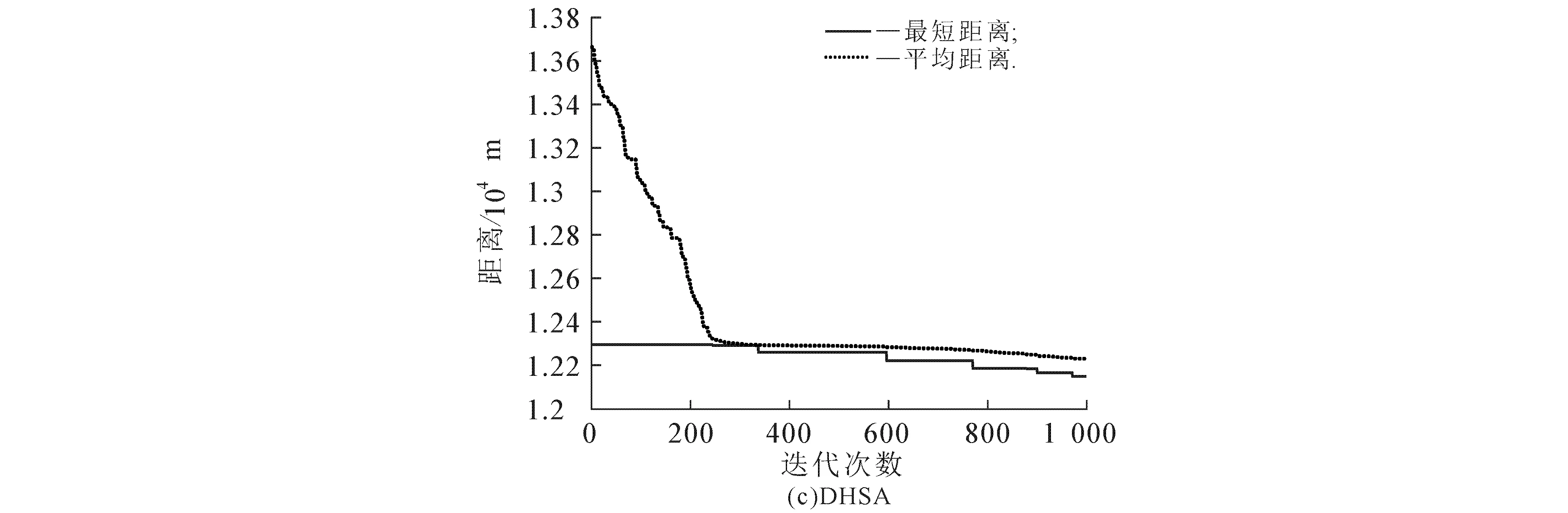
(ⅲ)生成一个随机数r(r∈[0,1])，若r

(2)

其中q为城市序号.

(ⅳ)若r≥PHMCR，则随机生成1个城市，得到1个新解.随机生成公式为

Xnew=Xq+θ(Xj-Xq)，

(3)

其中θ服从(0,1)均匀分布，j为城市序号.

(ⅴ)采用轮盘赌选择算法比较当前获得的最新路径值f(Xnew)与TSP路径库的最差路径值，若最新路径值小于最差路径值，则替换之，否则不作改变.

(ⅵ)判断进化是否结束，符合条件时，输出当前最优城市序列，计算城市之间的距离；否则返回步骤(ⅲ).

DHSA的流程如图1所示.

4 仿真实验

实验运行环境：Intel(R) Xeon(R) Sliver 4110 CPU @ 2.10GHz(4处理器)，8G内存，Windows10操作系统，集成开发环境MATLABR2014b.HAS的参数设置：PHMCR=0.9，SHMS=300，PPAR=0.33.与HSA相比，DHSA的参数PHMCR设置为[PPARmin,PPARmax]范围内自适应调节，PPARmin=0.1，PPARmax=0.99.

选取TSP案例库中的2个经典数据集bayg29和ch150，城市个数分别为29和150，实验迭代次数1 000，种群大小30.对GA，HAS与DHSA进行仿真实验，结果如图2～5所示.

图2 基于bayg29数据集的最优路径连接Fig. 2 Optimal Path Connection Graph Based on Bayg29 Dataset

图3 基于ch150数据集的最优路径连接Fig. 3 Optimal Path Connection Graph Based on CH150 Dataset

图4 基于bayg29数据集的最优路径收敛Fig. 4 Optimal Path Convergence Graph Based on Bayg29 Dataset

图5 基于ch150数据集的最优路径收敛Fig. 5 Convergence of Optimal Path Based on CH150 Dataset

由图4和图5可见，相较于HAS和GA，DHSA的收敛精度更好.根据图2和图3，可得3种算法的最优路径距离(表2).

表2 3种算法的最优路径距离

从表2可知：在2个数据集中，利用DHSA获得的最优路径都最短.bayg29数据集中，DHSA获得的最优路径比HAS的少约763 m，比GA的少约2 940 m；ch150数据集中，DHSA获得的最优路径比HAS的少约668 m，比GA的少约34 070 m.

5 结语

为了提高HSA的收敛速度和准确度，设计了一个动态调节音调概率的新算法DHSA.为了验证DHSA的有效性，选取TSP案例库中的2个经典数据集bayg29和ch150，通过Matlab软件对GA，HSA，DHSA进行仿真实验，结果表明，相较于HSA和GA，DHSA在收敛精度方面更优，最优路径更短.后续工作考虑将微调候选解的方法与其他智能算法相结合，使得算法在解决大规模的TSP时具有更大的优势.