基于稀疏自编码器和高斯混合模型的手写数据集分类
2021-05-11马双宝高梦圆胡江宇贾树林董玉婕
马双宝,高梦圆,胡江宇,贾树林,董玉婕
(武汉纺织大学 机械工程与自动化学院,湖北 武汉 430200)
深度学习是当今较为火热的领域之一。对于大量的样本进行学习,深度学习网络比其他的机器学习算法表现结果更为出色,但是现实生活当中并没有大量的标签数据。人类可以对新的事物只需要观察一次,在下次出现时就可以清楚地进行辨认。因此在处理小样本问题,李飞飞等人[1]在2006 年提出了one-shot问题,并且利用了贝叶斯推测方法对小样本进行分类,并取得较好成绩,成为小样本学习的开端。C. Finn,P. Abbeel 等人[2]根据元学习模型,提出了MAML 算法,根据训练不同得到的先验知识来指导新的任务,该模型取得不错的泛化能力,但是该模型需要预先训练,对参数调节具有一定要求。Oriol Vinyals 等人[3]提出了匹配网络对数据进行聚类分析,该网络可以对多个类别进行判别。Pake Snel 等人[4]提出了基于原型网络的聚类算法,它是通过新数据对原型网络的距离来衡量数据的类别的一种聚类算法。该算法只是通过简单的欧式距离作为聚类的标准,对于有些样本来说,泛化能力较差。Sachin Ravi 等人提出了基于优化的模型采用LSTM 来对小样本问题进行优化求解,但是模型复杂度过高,对样本存在过拟合问题。
上述方法均没有对样本的维度进行降维处理,小样本数据进行特征提取,由于维度过高会导致过拟合问题,而且维度过高对计算带来巨大运算问题。针对上述问题,本文采用一种基于稀疏编码器降维算法,首先对数据进行低维压缩处理,防止样本数量过少导致过拟合问题,然后利用高斯混合模型对数据进行聚类分析。
1 相关模型
1.1 稀疏自编码器模型
传统的降维算法主要采用主成分分析法对数据进行降维处理。主成分分析法采用将线性相关的一些变量通过正交变换转化成为一组少量的线性无关的变量表示。该算法属于一种线性变换,但是现实生活当中的数据往往呈现非线性关系,因此降维后的效果往往不是很好。
本文采用自编码网络进行数据维度的自动压缩。自编码器是一种神经网络模型,该网络可以自动进行特征提取,不需要人为进行特征运算。自编码器是一种无监督学习方法,因此采用该网络对标签有无没有关系,它通过输入和输出的损失作为损失函数进行反向传播,是一种非线性的降维方法。在一定层度上能够保证输入和输出的大部分信息完整并且具有较强的泛化能力。

图1 采用PCA 将维度降低到20 图像

图2 采用中间层维度为20 图像

图3 采用中间隐藏层为16 图像
如图1-3 所示为采用PCA 降维算法和自编码器算法进行数据降维效果,从图中可以看出,将原始图像的特征维度同样压缩至20,采用PCA 算法进行图像复原,有些图片出现模糊,而采用自编码图片依然可以清晰看见。因此采用自编码器对数据降维效果好于PCA 算法。
自编码器由两部分组成:编码器和解码器。编码器对数据进行降维处理,编码器对数据进行重塑。中间隐藏层为我们需要进行降维处理的数据维度(见图4)。
为了在数据降维过程当中提取较好的特征,我们在损失函数中添加正则项增减网络的稀疏性(见图5-图8)。

图4 自编码器网络工作原理图

图5 隐藏层为32 的普通编码器损失曲线

图6 隐藏层为16 的稀疏自编码器损失曲线
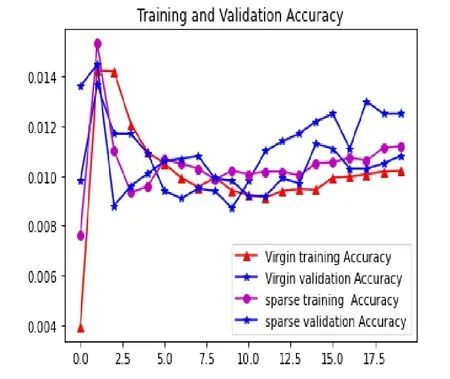
图7 中间隐藏层为32 的普通编码器精度曲线

图8 中间隐藏层为16 的稀疏自编码器精度曲线
从图5-图8 中可以看出,采用稀疏编码器的网络首先较快,而未采用稀疏编码器的网络收敛较慢,普通自编码器的网络过拟合比较严重。因此,我们采用稀疏编码器对原始数据进行降维处理。

图9 稀疏编码器中间隐藏层为2 原始图像与重建图像

图10 普通自编码器中间隐藏层为2 原始图像与重建图像
现在将中间隐藏层的维度降低为2,这样直接可以对数据进行可视化操作,但是将中间隐藏层的维度设置为2 时,经过解码器后图像变得比较模糊(见图9-图10),显然直接将中间隐藏层的神经元个数设置为2 不可行。首先将中间神经元个数设定某一值,让后再继续利用降维方法将维度继续降低。
1.2 T-SNE 算法
T-SNE 算法(t-distributed stochastic neighbor embedding,T-SNE)是一种无监督的降维算法。 T-SNE 算法能够有效对高位数据进行非线性降维。
假设n 维空间数据点{x1,x2,…,xN},则数据e 间的两两相似条件概率为:

利用梯度下降法对KL 进行迭代求解得到原始数据经过降维后的数据。图11 为利用T-SNE 算法将数据维度降为2 的图像。
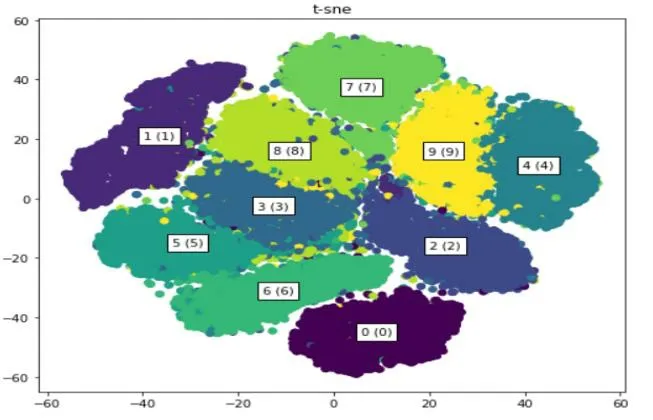
图11 利用T-SNE 算法将数据维度降为2 的图像
1.3 基于高斯混合模型原型聚类
经过T-SNE 算法将高位数据降维到2 维空间,现在需要对数据进行分析。
聚类算法属于无监督学习方法,该算法不需要对样本进行标记,通过数据的内在规律,对数据进行自动归类的一种算法。
Pake Snell 等人[4]利用基于原型的聚类算法对数据进行处理。该算法需要从数据集当中找一组初始化的原型向量,通过新数据与原型向量间的距离度量,找到离样本距离最近原型向量来进行类别划分。该算法性能好坏主要取决于原型向量选取与样本距离度量方式的选择。

其中Sk表示第k 个类别的样本数目,f∅表示映射函数,ck表示原型。
公式(6)代表利用映射函数f∅,将输入数据xi转换为特征向量,然后通过几组特征向量加和求均值得到原型向量ck。
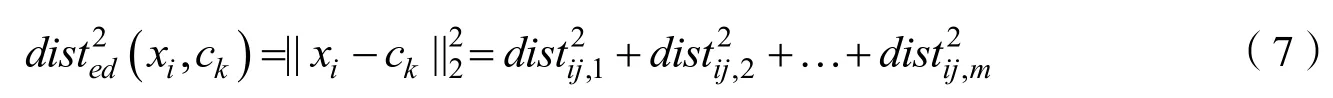
然后利用原型向量与新样本之间的欧式距离来度量样本的相似性。新的样本通过距离原型向量距离最小来划分到该原型网络的类别。该算法性能好坏取决于原型向量的选取。而且样本之间距离的度量采用欧式距离并不能准确表示样本差距,因此本文采用基于高斯混合模型的聚类方法。
高斯混合模型以概率为基础进行原型聚类,是典型的生成式模型。高斯混合模型采用多个多元高斯混合分布来估计样本的概率分布。
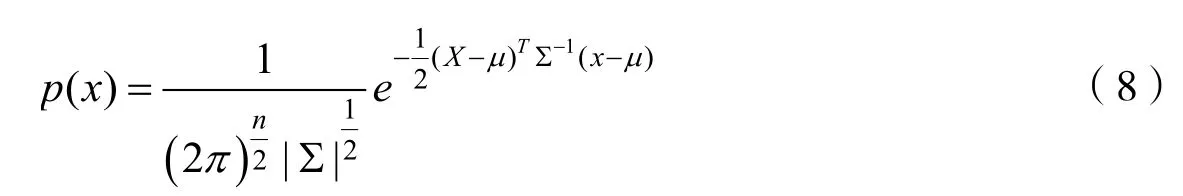
公式(8)表示多元高斯分布,其中μ,∑表示高斯分布的均值和协方差。
采用k 个类别的多元高斯混合分布来进行数据的概率密度估计。其定义的分布为:

其中,μi,∑i表示第 i个高斯分布的期望与协方差,αi表示取得第i个混合成分的概率。
高斯混合模型是典型的生成概率模型:首先根据αi选择第i个混合成分,让后根据相应混合成份来生成数据。设样本xj在k 个族中划分的标记为λj。采用高斯混合模型进行聚类时,我们进行优化求解采用最大后验概率,即给定样本xj是第i个混合成分生成的后验概率γij的最大化。

由于等式当中含有隐变量αi,因此采用EM 算法进行求解。该算法分两步:E-Setp,求期望;M-step,计算新一轮的模型参数估计值。重复E-Step 和M-Step 直到模型收敛。
E-Step:依据当前的参数,计算每个j数据来自子模型k 的可能性。

通过不断更新E-Step 和M-Step,最终得到收敛,求解极大后验概率值。
2 仿真实验与分析
本文首先采用稀疏自编码器对数据进行降维处理,由于将中间隐藏层维度设置为2,经过解码器图像已经变得模糊,采用T-SNE 算法对中间隐藏层维度继续进行降维处理得到二维图像。采用高斯混合模型对二维数据进行极大后验概率估计,由于含有隐变量,采用EM 算法进行迭代求解,最后得到聚类结果。在稀疏编码器设计输入数据的维度为128,全连接层有两层,维度分别为64 和16,解码器和编码器结构对称。为了增加自编码器的稀疏性,在中间隐藏层加入L1 正则化。正则化会使很多隐藏层神经元权重变为0,使得神经元变得稀疏。采用交叉熵作为损失函数来作为输入数据和输出数据的损失函数。采用Adam 作为优化器,每次喂入神经元数据为128,迭代50 次。在经过T-SNE 算法和高斯混合模型时,类别个数设置为10。本文采用的数据集为mnist 手写数据集,该数据集公共有60000 张测试图片和10000 张训练图片,每张图片的大小为28*28。
为了进一步探讨,采用卷积神经网络对手写数据集进行分类。
3 实验结果与分析
利用上述方法对手写数据集进行聚类结果如图12-图15 所示。图16 和图17 为稀疏自编码器损失曲线和精确度曲线。在训练集训练精度为0.89025,在测试集的训练精度为0.896。从图16 和图17 中可以看出,采用稀疏编码器的损失曲线和精确度曲线差别不大,对数据进行降维处理在一定程度上防止了数据的过拟合。

图12 手写数字0 聚类

图13 手写数字1 聚类

图14 手写数字2 聚类
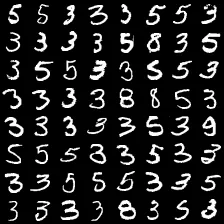
图15 数字3 聚类结果

图17 稀疏自编码器网络准确度曲线

图18 采用卷积神经网络损失曲线
从图16-图19 中可以看出,采用卷进神经网络在训练集和测试集合出现过拟合,而采用稀疏自编码器网路训练集和测试集曲线能够很好拟合。本文采用的稀疏自编码器网络对数据降维,和高斯混合模型对数据集进行聚类均为无监督学习算法,因此不需要预先知道样本的标签,具有较好的自适应能力。但是,在精度上,采用卷积神经网络优于本文算法。
4 总结
本文采用稀疏编码器对数据进行降维处理,中间隐藏层维度设置为2,对数据进行可视化,然后再利用解码器进行图像解码,但图像模糊。因此直接中间隐藏层神经元个数设置为2 不合适,需要进一步进行降维。考虑到本文采用无监督算法,因此采用T-SNE 算法对中间隐藏层数据进行降维处理。然后采用高斯混合模型对数据进行降维处理。在整个算法的过程当中,都是无监督学习,因此不需要数据对应的标签,减少了人工成本。本文算法不足之处在于并非一种完全端到端学习。在对小样本学习探索中,缺乏对多个类别小样本的探索。在精度方面低于卷积神经网络,需要对模型进行优化,进一步提高精度。
