单回转双回开断塔下方的工频电场分布及其影响因素研究

盛金马,姜克儒,刘 军,常 江,夏新运,崔宇豪

(1.国网安徽省电力有限公司 经济技术研究院,安徽 合肥 230001; 2.国网安徽省电力有限公司,安徽 合肥 230022; 3.安徽华电工程咨询设计有限公司,安徽 合肥 230000; 4.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

随着电网规模的不断扩大,社会环保意识的增强,输电线路的电磁环保问题引起了广泛关注。优化杆塔结构,控制线路下方的电场强度值,成为架空线路设计的关键环节之一[1-2]。单回转双回架空线路开断塔(转角塔)可将单回线路开断后,转角90°形成双回线路继续走线,可避免双回路分支杆塔的使用,无需改变相邻杆塔的导线布置方式[3]。这种杆塔的使用可减少塔基占地面积,节约线路经济成本。由于开断塔的特殊结构和塔上的线路转向,这种杆塔下方的电场分布与常规杆塔显著不同,特别是线路发生交叉跨越或邻近建筑物时,开断塔附近的电场问题更为突出[4-5]。计算开断塔附近的电场分布,分析影响开断塔下方电场强度的因素,对开断塔及其架空线路的优化设计具有重要意义。

目前国内常见的计算架空线路工频电场的方法有模拟电荷法、有限元法、矩量法等。文献[1]建立了3种同塔双回直线塔二维模型,研究了输电线路导线表面和线路下方的电场强度;文献[6]建立了输电线路与建筑物的位置变化二维模型,使用有限元法研究了输电线路临近不同高度房屋时的电场强度;文献[7]建立了特高压输电线路工频电场计算的二维仿真模型,探讨了降低线路下方电场强度的方法。以上研究均基于二维模型对线路周围的电场分布进行求解,基于二维模型的求解方法对于普通直线塔的计算结果误差较小,但对于架空线路开断塔周围的电场分布问题,该方法已不适用,原因是架空线路在开断塔部位会转角90°并形成同塔双回路走线,这种部位的电场求解必须从三维空间上考虑线路走线情况。文献[8]建立了三维输电线路模型,结合模拟电荷法和矩量法采用了模拟电荷矩量法,研究了影响线路下方工频电场的因素;文献[9]建立了同塔双回直线转角塔三维模型,研究了转角塔在3种导线相序组合情况下的电场差异,由于其考虑的架空线转角度数较小,且忽略了架空导线弧垂,不能准确评估导线距地面高度变化对线路下方电场的影响。随着经济发展和电网结构的复杂变化,大转角开断塔的工程应用需求凸显,有必要开展杆塔的三维工频电场分布及其影响因素研究。

本文选择110 kV单回转双回架空线路开断塔进行等比例几何建模,采用有限元计算方法进行三维工频电场计算,对比了开断塔跳线串绝缘子的表面电场强度的控制要求以及常规直线塔与开断塔下方电场强度,分析了导线相序组合、导线水平相间距离、横担高度、风偏对开断塔下方地面附近电场分布的影响,研究结果能够为开断塔的设计提供参考。

1 研究方法

1.1 计算方法选择

对于普通直线塔的电场分析计算,在忽略杆塔上绝缘子等结构的影响,并将线路简化为二维模型时,模拟电荷法较为适用。而对于单回转双回开断塔,既要关注输电线路下方的电场分布,又要关注塔上跳线串绝缘子、地电位作业人员的表面电场分布情况。这是一种求解多介质、复杂边界条件的场域问题,有限元法具有独特的优势[9]。计算方法如下:首先适当划分求解域,将连续问题转化为离散问题;然后对每一个网格用不同的函数表示;最后通过求解代数方程计算所求问题的近似解。本文采用有限元仿真软件Comsol进行计算分析。

架空线路运行在工频50 Hz下,所处的电磁场环境随时间变化较缓,相邻两杆塔之间的架空线路长度通常为数百米,当电磁波的波长远大于架空线路长度时,可以忽略磁场对电场的影响,视为电准静态场。电准静态场问题的求解可归结为一定条件下寻求拉普拉斯方程解的过程[10],由高斯定律(1)式带入(2)式可得电位φ的拉普拉斯方程(3)式,即

D=ρ

(1)

D=εE

(2)

(3)

1.2 电场环境控制要求

依据文献[11-12]当输电线路穿越居民区,线路附近地面1.5 m高度处的工频电场强度应控制在4 kV/m以内。

绝缘子串同样存在电场控制要求[13]。对于曲率半径较小的连接金具,其控制场强定为峰值下不超过23 kV/cm;对于均压环、屏蔽环等曲率半径较大的金具,其控制场强定为峰值下不超过 20 kV/cm;对于绝缘子伞裙等导线侧护套表面电场强度一般不超过4 kV/cm(有效值)。

2 几何建模及边界条件设置

2.1 几何建模

开断塔几何模型如图1所示。

图1 开断塔几何模型

开断塔的塔高46.2 m,双回路三相横担的高度分别为40.7 、37.0 、30.0 m,水平方向的单回路架空线通过耐张串和跳线串转角90°后形成垂直方向的双回架空线。根据开断塔的设计图纸在三维绘图软件SolidWorks中建立等比例几何模型(图1a)。该模型包含了杆塔、耐张串绝缘子、跳线串复合绝缘子以及均压环等金具,导线采用LGJ-400型钢筋铝绞线,半径为12 mm。本文的关注点在于跳线串绝缘子周围以及线路下方的电场分布,为提高计算效率,对开断塔进行了如下简化(图1b)：

(1) 杆塔主体结构由(片状)角钢简化为面状钢板,横担部分简化为实心结构。

(2) 简化悬垂串、耐张串与杆塔相连接的挂环等尺寸较小的结构件。

为了对比常规直线塔与开断塔下方的电场强度,保持直线塔整体尺寸与开断塔一致,仅删去水平方向的横担和架空导线及其相应的绝缘子,直线塔几何模型如图2所示。带支撑管跳线串由复合绝缘子、均压环、钢管等组成,取中横担右侧的跳线串,跳线由跳线串连接至中横担耐张串,如图3所示。

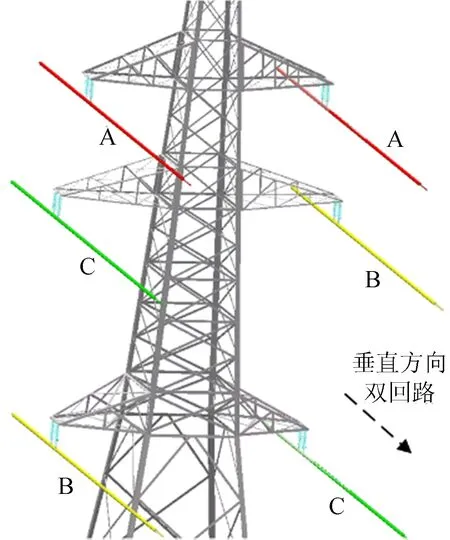
图2 直线塔几何模型

图3 带支撑管跳线串

2.2 模型材料设置

开断塔塔身为钢材质,架空线为钢芯铝绞线。根据趋肤效应,电流沿着架空导线外层的铝绞线传导,在模型中可将架空导线的材料设置为铝。跳线串起电气隔离作用,绝缘子伞裙为复合绝缘子,内部为玻璃纤维增强环氧芯棒,外部为硅橡胶。由于玻璃纤维增强环氧芯棒材料与硅橡胶材料的电导率和介电常数都很小(考虑填料因素后,其相对介电常数小于10),且差别也很小,对电场分布的影响可以忽略,因此将绝缘子的材料统一设置为硅橡胶。

地电位作业人员人体模型由躯干和头脑组成,其中,脑组织、颅骨、头皮共同组成头脑部分,如图4所示。人体组织的介电常数和电导率见表1所列[14]。

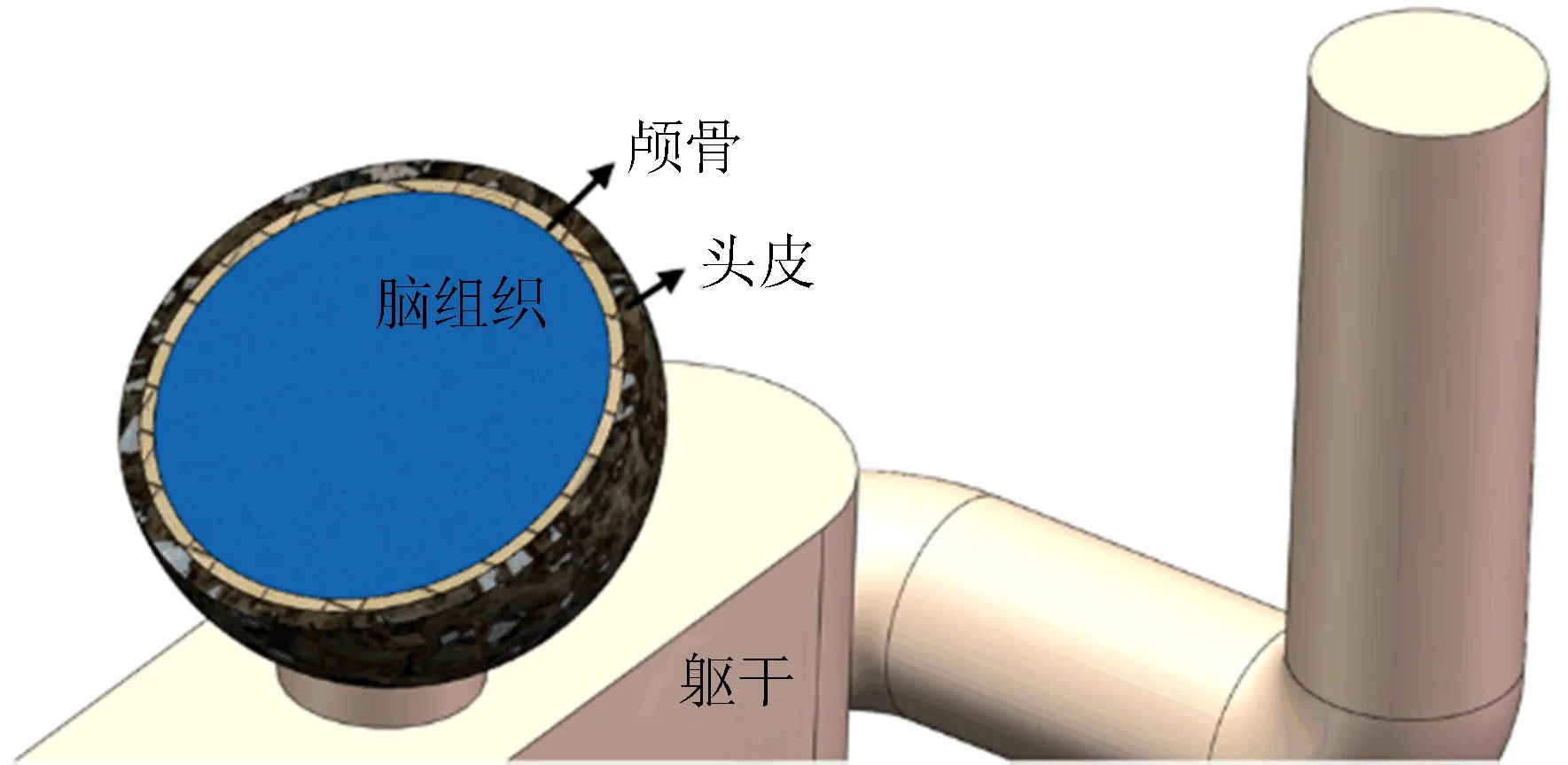
图4 人体模型

表1 人体组织介电常数及电导率

2.3 边界条件设置

开断塔输电线路的电压等级为110 kV,根据相电压与线电压之间的数量关系[15],可得A、B、C三相瞬时电压值为:

UA=90cosωt，

(4)

由于工频输电线路的电场环境可看作是准静态场,取零时刻的瞬时电压90 、-45 、-45 kV分别作为三相线路的电压,架空地线和塔身设置为接地。

3 计算结果与分析

3.1 跳线串绝缘子的表面电场分布

开断塔的电场分布计算结果如图5所示,整个杆塔周围电场强度的最高区域位于上横担和中横担之间的导线悬挂区域。此外,下横担的杆塔悬挂区域电场强度也较高。跳线串电场分布图如图6所示。区域内,跳线串电场强度最大值出现在绝缘子上端(低压侧)与金具连接处(图6a),最大值为7.95 kV/cm,满足23 kV/cm的场强控制要求;均压环处电场强度最大值点出现在右外侧,最大值为4 kV/cm,满足20 kV/cm的场强控制要求;绝缘子伞裙上电场强度最大值点出现在靠近高压侧第2节(大)伞裙边缘处,最大值为1.95 kV/cm,满足4 kV/cm的场强控制要求。

图5 杆塔截面电场分布

图6 跳线串电场分布

均压环影响着绝缘子串的电场分布[16-18]。未装配均压环跳线串电场强度最大值出现在绝缘子下端(高压侧)与金具连接处,最大值为18.39 kV/cm,远大于(装配均压环)跳线串场强最大值;其绝缘子伞裙上电场强度最大值点出现在靠近高压侧第1节(小)伞裙边缘处,最大值为2.09 kV/cm,同样大于(装配均压环)绝缘子伞裙场强最大值。有(无)均压环的跳线串各位置的电场强度最大值见表2所列,由表2可知,均压环可起到均匀电场、降低场强最大值的作用。

对于(装配均压环)的跳线串,其金具、伞裙、均压环的场强最大值点均在跳线串的右侧,见表3所列,这是由于跳线与架空导线电气连通,绝缘子附近的场强与绝缘子距跳线的距离平方成反比,右侧绝缘子距跳线的距离小于左侧绝缘子距跳线的距离,故右侧绝缘子场强最大值大于左侧绝缘子场强最大值。

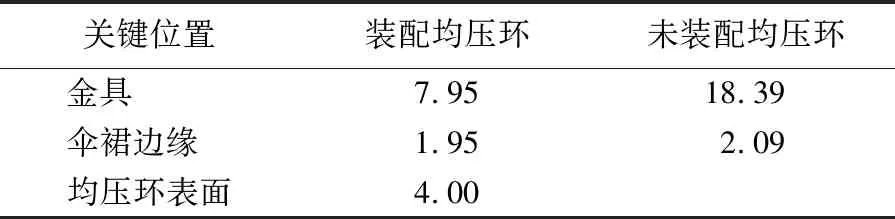
表2 有(无)均压环的跳线串各位置电场强度最大值 kV/cm

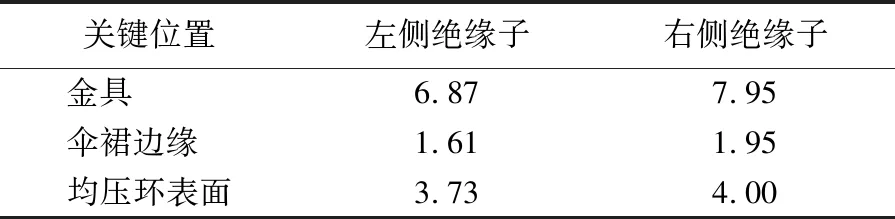
表3 跳线串两侧绝缘子各位置的电场强度最大值 kV/cm

3.2 导线相序组合对开断塔下方电场的影响

水平方向的单回架空线路经开断塔转角90°后可形成3种双回路相序组合,如图7所示,从上往下排列形成的3种相序组合依次为:① 同相序组合ABC-ABC;② 异相序组合ABC-BCA;③ 逆相序组合ABC-CBA[19-20]。计算3种相序组合下转角塔和直线塔下方的电场强度,结果如图8所示,开断塔下方距地面1.5 m处的场强最大值为0.12 kV/m,位于距开断塔中心水平方向11 m处,常规直线塔下方的场强最大值为0.09 kV/m,位于距开断塔中心水平方向9 m处,开断塔下方的电场强度高于普通直线塔下方电场强度,即架空线路转角90°并形成双回路后会导致下方电场强度增大。

图7 不同相序组合示意图

图8 导线相序组合对场强分布的影响

同相序组合方式下,开断塔下方电场场强最大值为0.12 kV/m;异相序组合方式下,开断塔下方电场场强最大值为0.08 kV/m;逆相序组合方式下,开断塔下方电场场强最大值为0.07 kV/m。对比上述计算结果能够看出,相序组合一致时,开断塔下方电场强度大于直线塔下方电场强度,开断塔下方的电场强度最小的相序组合方式为逆相序组合。

3.3 水平相间距离对开断塔下方电场影响

架空导线相间距离同样影响杆塔下方电场强度分布[21-22]。以逆相序组合为例,导线相间距离示意图如图9所示。

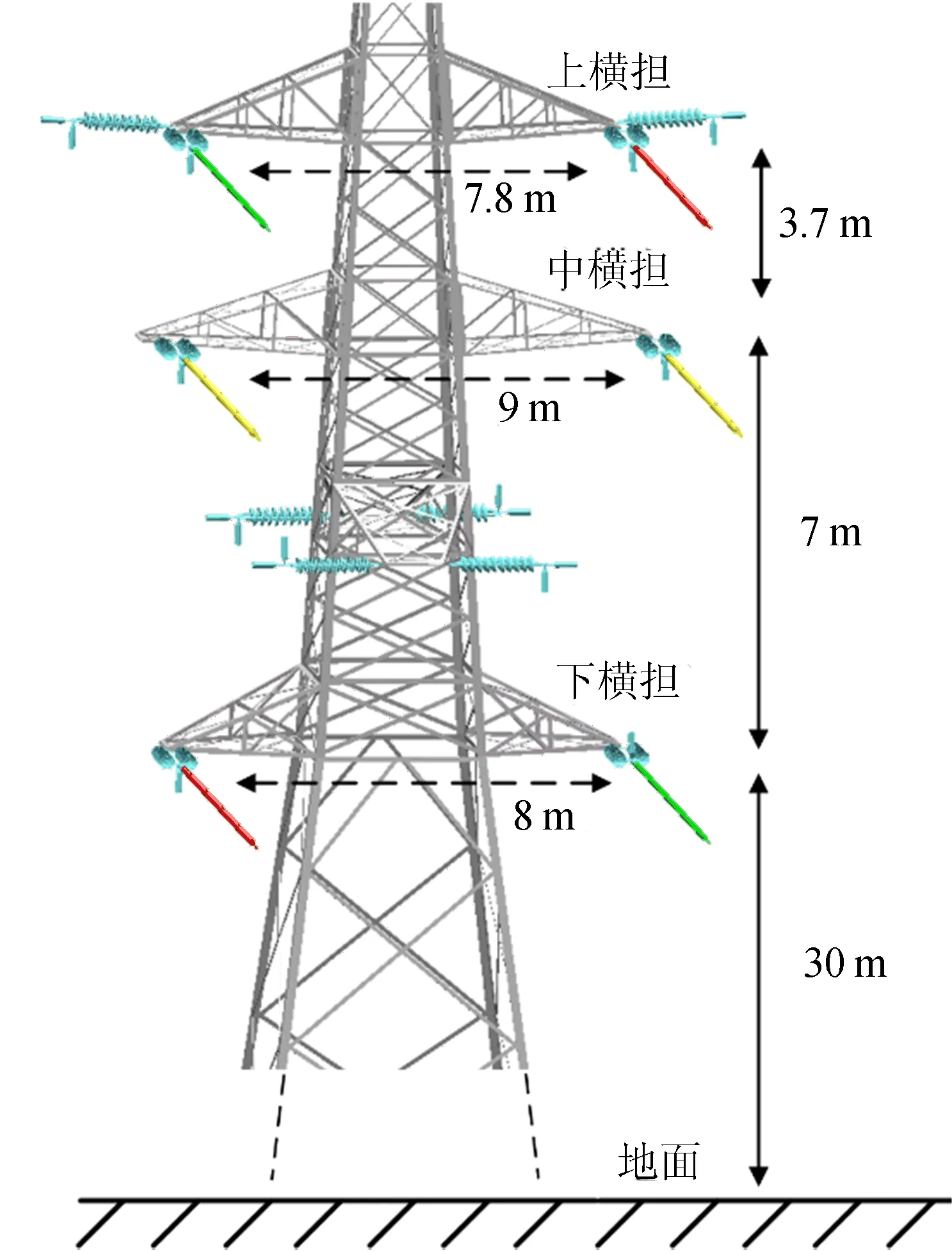
图9 导线相间距离示意图

图9中,分别改变悬挂在上横担、中横担、下横担上的导线相间距离,获得3组相间距离,见表4所列。计算3组相间距离下转角塔和直线塔下方的电场强度,结果如图10所示,相间距离相同时,开断塔下方电场强度大于直线塔下方电场强度。当相间距离组合为5.8、7.0、6.0 m时,开断塔下方电场强度最大值为0.063 kV/m;当相间距离组合为7.8、9.0、8.0 m时,开断塔下方电场强度最大值为0.07 kV/m;当相间距离组合为9.8、11.0、10.0 m时,开断塔下方电场强度最大值为0.077 kV/m。开断塔上同一横担上的导线水平相间距缩短4 m时,杆塔下方电场强度减小幅度约为22.2%。根据上述计算结果,导线水平相间距离相同时,开断塔下方电场强度大于直线塔下方电场强度,开断塔下方电场强度随着同一横担上导线水平相间距离的减小而减小。

表4 电场计算采用的3组导线水平相间距离 m

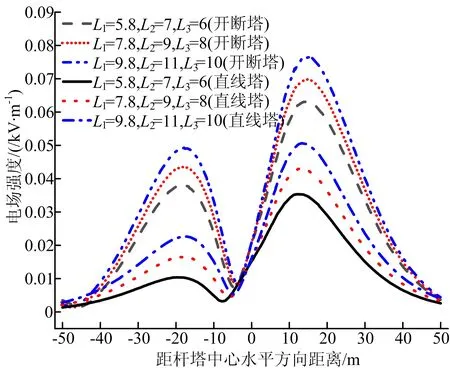
图10 相间距离变化对场强分布的影响

3.4 横担高度对开断塔下方电场的影响

以开断塔下横担为分界,保持下横担以上结构尺寸不变,只改变下横担至地面的高度,分别为28、30、32 m(取逆相序、相间距离组合为7.8、9.0、8.0 m),计算3种高度情况下开断塔和直线塔下方的电场分布,结果如图11所示,横担高度相同时,开断塔下方电场强度大于直线塔下方电场强度。当下横担高度为28 m时,开断塔下方地面附近电场强度最大值为0.086 kV/m;当下横担高度为30 m时,开断塔下方电场强度最大值为0.07 kV/m;当下横担高度为32 m时,开断塔下方电场强度的最大值为0.06 kV/m。上述3个横担高度的开断塔下方电场强度均满足4 kV/m的电场控制要求。横担高度增加4 m,开断塔下方电场强度减小幅度约为40%。上述计算结果表明,横担高度相同时,开断塔下方电场强度大于直线塔下方电场强度,开断塔下方电场强度随着横担高度的增加而减小。

图11 横担高度变化对场强分布的影响

3.5 风偏对开断塔电场强度的影响

在实际运行环境中,风偏使跳线串偏离原有位置,缩短导线与塔身的空气间隙,可能会引起空气击穿,进而造成线路跳闸事故,因此需要考虑最大风速下导线与杆塔的空气间隙是否满足绝缘要求[23-24]。文献[24]考虑风偏脉动效应,按照最大风速(28 m/s),通过有限元计算得出绝缘子风偏角极值为64.6°。本文选取64.6°为最大风偏角,如图12所示。

图12 跳线串风偏角示意图

跳线串长度为L(均压环位于4L/5处),风偏致跳线串偏离竖直方向的夹角为θp,导线距横担距离Sp1、导线距塔身距离Sp2满足如下公式:

Sp1=0.8Lcosθp

(5)

Sp2=3.43-Lsinθp

(6)

0°≤θ≤64.6°

(7)

当θmax=64.6°时,导线与横担距离最短,Sp1=0.4 m,依据棒-板(不均匀电场)空气间隙的工频击穿电压和间隙距离之间的关系曲线[25],0.4 m空气间隙的击穿电压为148 kV,远大于单回转双回开断塔相电压最大值90 kV。由以上分析可知,最大风偏角下,导线与杆塔之间的空气间隙能够满足绝缘要求。

对比跳线串不同风偏角下(选取15°、30°、64.6°)地电位作业人员攀登至与跳线串等高处的人体体表电场分布(同时考虑攀登直线塔的情况)。不同风偏角下人体体表电场分布如图13所示。

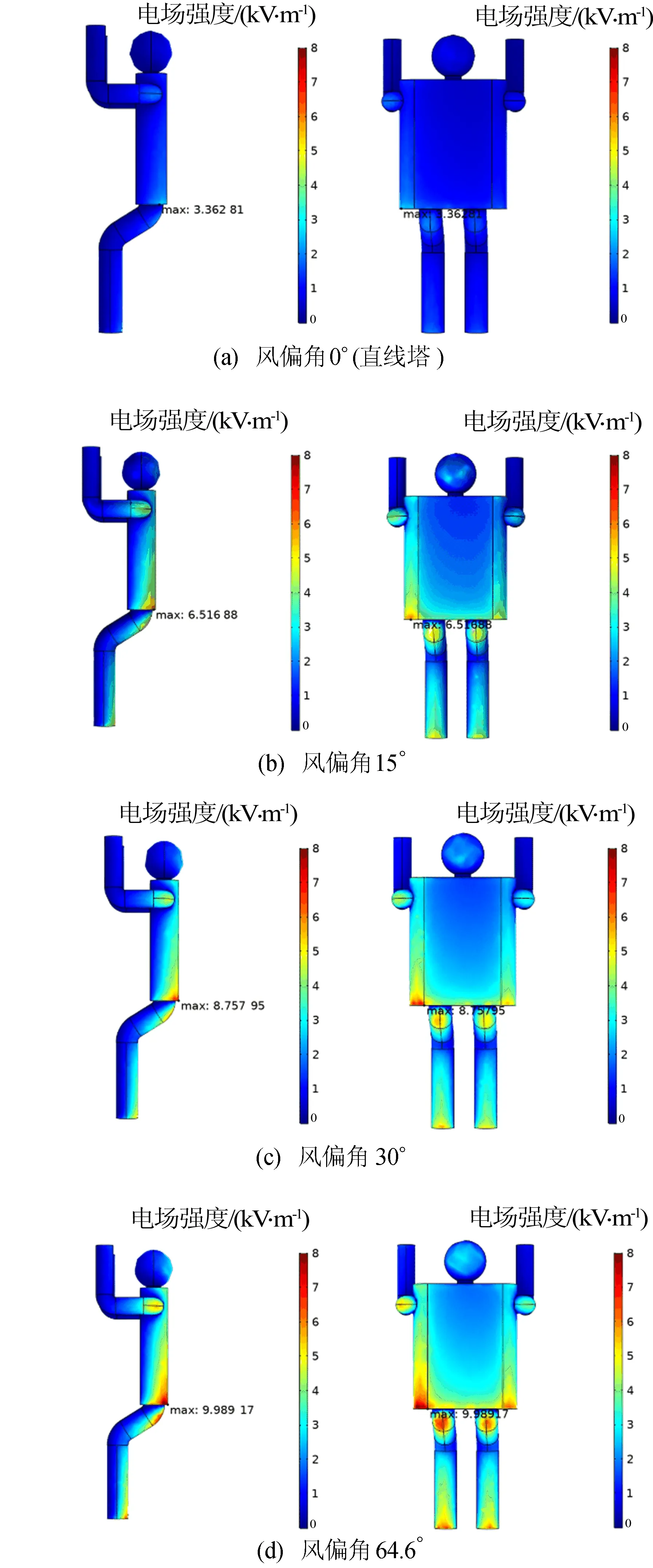
图13 不同风偏角下人体体表电场分布

由图13可知,不同风偏角下人体体表场强最大值均位于人体背部左下角(这是由于人体背部距跳线距离最短),直线塔上的人体体表场强最大值为3.36 kV/m,跳线串风偏角15°时的人体体表场强最大值为6.51 kV/m,跳线串风偏角30°时的人体体表场强最大值为8.75 kV/m,跳线串风偏角64.6°时的人体体表场强最大值为9.98 kV/m。随着跳线串风偏角的增大,地电位作业人员体表电场强度随之增大,最大场强未超过人体外露部位场强限值(240 kV/m)[26]。

不同风偏角下距地面1.5 m高截面电场分布如图14所示,跳线串风偏角15°、30°、64.6°的杆塔下方距地面1.5 m高截面的电场分布一致。上述计算结果表明,随着跳线串风偏角的增大,导线与杆塔之间的空气间距随之减小,风偏角达到最大值64.6°时,导线与杆塔之间的空气间隙能够满足绝缘要求;地电位作业人员体表电场强度极值随着跳线串风偏角的增大而增大,但始终小于人体外露部位场强限值(240 kV/m);开断塔下方距地面1.5 m高截面电场不随跳线串风偏角的变化而变化。

图14 不同风偏角下距地面1.5 m高截面电场分布

4 结 论

本文对110 kV单回转双回架空线路开断塔进行了三维工频电场计算,对影响杆塔下方地面附近电场强度的4个因素(导线相序组合、导线水平相间距离、横担高度、风偏)进行了对比分析,得出如下结论:

(1) 相同影响因素下,开断塔下方电场强度大于直线塔下方电场强度。

(2) 开断塔上的架空导线采用同相序组合,其下方场强最大;采用逆相序组合,其下方场强最小。建议开断塔转角90°后的双回路走线采用逆相序组合的方式。

(3) 随着同一横担上架空导线水平相间距离的减小,开断塔下方地面附近电场强度也随之减小。建议在留有足够绝缘距离的前提下,适当减小开断塔架空导线的水平相间距离。

(4) 横担高度增加,开断塔下方地面附近电场强度随之减小。若改变相序组合和改变相间距离都无法有效降低杆塔下方的电场强度,可在经济成本允许的条件下,适当增加横担高度。

(5) 随着跳线串风偏角的增大,导线与杆塔的距离随之减小,风偏角达到最大值64.6°时,导线与杆塔之间的空气间隙能够满足绝缘要求;地电位作业人员体表电场强度极值随着跳线串风偏角的增大而增大,但始终未超过人体外露部位场强限值(240 kV/m);开断塔下方距地面1.5 m高截面电场不随跳线串风偏角变化而变化。