超深地下连续墙施工槽壁局部稳定判据

李志文 魏刚 郭运华 李毅阳

摘要：地下连续墙槽段开挖为连续下切的动态过程，槽壁稳定性控制仍依赖于工程实践经验，缺乏成熟的理论指导，槽壁失稳事故时有发生。基于泥浆渗透成膜实验成果及有效护壁压力的动态演化规律，研究了槽壁土体在旋转破坏模式下的富余护壁压力分布规律，获得了槽壁稳定性控制因素及稳定性控制条件，建立了泥浆护壁条件下以土体等效内摩擦角、开挖深度及开挖下切速率、泥浆黏度及重度为参量的槽壁稳定性判据，揭示了槽壁稳定施工的关键控制要素。研究成果在福州地铁5号线建新南路60 m深地下连续墙工程中的应用表明：地表以下10 m内及开挖面以上3 m范围为槽壁稳定性薄弱环节，与现场实际吻合，以富余护壁压力为依据的槽壁稳定判据可较方便地指导施工作业。

关键词：地下连续墙;槽壁稳定;稳定性判据;泥浆护壁;旋转型破坏

中图法分类号：TU753文献标志码：ADOI：10.15974/j.cnki.slsdkb.2021.04.008

文章编号：1006 - 0081（2021）04 - 0049 - 05

1 研究背景

地下连续墙是一种在泥浆护壁的协同作用下采用机械开挖出深而狭窄的沟槽，并及时进行混凝土灌注的连续地下墙体，具有施工效率高、污染少、防渗强等优点，已逐渐被运用于工程建设中。槽壁稳定控制问题是这一施工方法的技术关键，为解决这一技术难题，部分学者从槽壁滑动体的力学平衡分析方面研究槽壁稳定控制方法。Washbourne[1]、季冲平等[2]、张厚美等[3]运用三维滑动体的平衡分析方法，进行槽壁滑动体的受力分析，得到了不同模式下护壁泥浆最小重度的计算方法;Wong等[4]、Hajnal等[5]运用槽壁两侧土压平衡分析法，比较槽壁两侧泥浆有效压力pmax与竖直面的土压力px相互作用情况来判断槽段的稳定性;刘国彬等[6]、姜朋明等[7]运用单元土体应力极限状态分析法，通过把槽壁单元体上的摩尔应力圆的半径r1与处于极限平衡状态下与抗剪强度相切的摩尔应力圆半径r2的比值进行分析，来判断槽壁稳定性。

另一部分学者研究了泥浆有效护壁压力的形成机制。李建军等[8]、杨春鸣等[9]进行护壁泥皮的抗渗性能试验，得到了在不同渗透时间、泥浆容重以及不同压差时的泥皮最大抗渗力px;叶伟涛等[10]、靳利安等[11]基于抗渗泥皮有效护壁压力的试验结果，从泥浆成皮的压差条件及关于时间演化规律出发，研究不同开挖深度泥浆有效护壁压力的分布规律，以及含砂率对泥浆成膜的影响。丁勇春等[12]对地连墙不同施工阶段槽壁土体应力状态进行分析研究。

基于泥膜有效护壁压力的时间-空间演化的“驼峰”型分布规律，假定槽壁滑动面为旋轮线破坏模式，研究泥浆富余护壁压力沿槽壁深度的空间分布规律，并建立槽壁稳定性判据，以指导现场施工。

2 泥浆有效护壁压力的分布形态

靳利安等[11]研究了泥膜成膜环境对有效护壁压力的影响，并得出了不同开挖深度条件下的有效护壁压力沿槽深的函数关系，但没有计入泥浆黏度的影响，这里将泥浆黏度纳入影响因素研究泥浆有效护壁压力。

泥膜的最大抗渗力与成膜渗透压差关系：

[Pmax=-0.0049D-1+0.375]              （1）

式中：[Pmax]为泥皮可承受的最大抗渗压力，MPa;D为泥皮两侧的渗透压差（泥浆与地下水压力之差），MPa。考虑到泥浆沉淀因素影响，根据福州地铁5号线不同槽段数据统计，泥浆沿深度方向每10 m泥浆容重增加1%，则泥浆成皮压力随深度的分布关系有：

[D=γ1+0.001l2l2-γwl1]    （2）

式中：[γ]为泥浆初始重度，kN/m3;[l1]为计算位置距地下水面距离，m;[l2]为计算位置距泥浆液面距离，m。泥皮最大抗渗力随静置时间的增长函数关系为

[Pt=-0.41×t+2-0.55+0.375]          （3）

式中：Pt为泥皮可以承受的抗渗力随时间的变化值，MPa， 极限值为0.49MPa; t为泥皮成型时间，h。泥膜最大抗渗力与泥浆黏度增长函数关系为

[Ps=-10.84×e-0.225s+0.375]            （4）

式中：Ps为泥皮可以承受的抗渗力随泥浆黏度的变化值，MPa;s为泥浆黏度，s。当计入泥浆黏度对最大抗渗力的影响后，可得到泥皮的有效抗渗压力[P有效]与D、t、s相关的函数关系式为

[P有效=0.375-0.0049D-11-28.9e-0.225s1-1.1×t+2-0.55]                          （5）

典型有效护壁压力沿槽深分布形态如图1所示。

图1表示不同开挖深度条件下，泥浆有效护壁压力沿槽深方向的分布形态。随着开挖深度增加，槽壁上有效护壁压力可分为3段：①靠近地表段，随深度线性增加，表明有效护壁压力受泥浆重度影响;②线性段以下至開挖面以上10 m范围，为护壁压力增加段，表明有效护壁压力受泥膜的质量控制;③开挖面以上10 m范围内，为有效护壁压力的快速衰减段，表明由于泥浆成膜时间较短，有效护壁压力增长幅度有限。整体上看，有效护壁压力沿深度方向呈“驼峰”型分布形态。

3 局部失稳模式下槽壁土体主动土压力

直线型滑裂面的库伦土压力理论[13-14]是当今设计挡土墙的主要依据，部分学者的研究[15-16]表明：挡土墙失效时，其后方土体滑裂面的曲线特征与对数螺旋线、旋轮线相似，槽壁局部失稳模式一般呈旋轮线形态。

假设当挡土墙墙后土体处于极限平衡状态时，土体内部将产生通过墙脚的旋轮线滑裂面，如图2所示，其方程为

[x = R（θ-sinω）y = R1-cosω]                         （6）

式中：R为旋转半径，m;[ω]为旋轮线转角，（°）。

旋轮线上任意一点的斜率可表示为

[tanθ=dydx=tanπ2-ω2]                   （7）

旋轮线上任意点的切线与水平方向的夹角为

[θ = π2 - ω2]                             （8）

如图3所示，在地表以下深度为y处取一厚度为dy的微小单元体，微分单元顶面受垂直向下的压力py，地面受竖直向上的反力py+dpy，单元体自重为dw，假设泥浆渗透范围与原状土间的摩擦力为[τ1]，垂直于滑动面的不动土体反力r，挡土墙的水平反力，即主动土压力为px，[τ2]为破坏面处的摩擦力。

由旋轮线上任意点的切线与水平方向的夹角公式，可知當旋轮线转角为0时，即x=y=0时，θ=90°;在墙脚处，旋轮线转角为120°时，θ=30°。当旋轮线通过墙趾时，旋轮线转角为120°，θ=30°，可得旋轮半径：

[R=H1-cosω=2H3] （9）

对于滑裂面任意[y0]处：

[ω=arc1-y0R=arc1-3y2H]        （10）

将式（10 ）带入式（8）中，可得：

[θ = π2 - arc1-3y2H2]                  （11）

式（11）即为开挖深度与微元体滑裂角之间的关系式。

水平微分单元上表面长度为

[DE=b1=H-ycotθ]              （12）

水平微分单元下表面长度为

[GF=b2=H-y-dycotθ]          （13）

水平微分单元自重为

[dw=b1+b22dyγ]                  （14）

考虑微分单元体在x方向的受力为

[px+τ2 cotθ-r=0]                   （15）

考虑微分单元体在y方向的受力为

[dpydy=γ+1H-ypy- r -τ1+τ2tanθ]   （16）

对于无黏性土，各参数为

[px=Kpy， τ1=pxtan δ， τ2=rtanφ]         （17）

对于黏性土，引入等效内摩擦角[17]，根据主动土压力相等原理的土层等效内摩擦角计算公式为

[φD=90°-]

[2tan-1tan245°-φ2-4Ctan45°-φ2γH+D+4C2γ2H+D2] （18）

式中：[φD]为等效内摩擦角，（°）;[φ]为土体内摩擦角，（°）;C为土体内聚力，MPa;[γ]为土体重度，kN/m3，H为埋深，m;D为挡土墙插入深度，m;这里取为0。

将式（17）代入式（15）和（16），可得：

[dpydy=1-cosθ-2φsinθ-φKtanθcosφpyH-y+γ]  （19）

由O点的力矩平衡可得：

[pxLIody+τ2LOMLEF+bbdpy-dw2]=0      （20）

将式（14）和式（17）带入式（20）化简得：

[Kpydybtanθ+τ2bdysin2θ+bdpy-γbdy=0]   （21）

等式两端除以[dyb]得：

[dpydy=γ+1b2Kpytanθ+2Kpytanθ1-cotθ tanφsin2θ      =γ+2Kpyb tanθ1+tanφ tanθ1-cotθ tanφsin2θ]

（22）

由式（19）和式（22）联立可求出土侧压力系数K为

[K=12+2tanφ tanθ1-cotθ tanφsin2θ+tanθcosφcosθ-2φsinθ-φ]

（23）

[px=K（q-γHαK-2）（H-yH）αK-1+γ（H-y）αK-2]

（24）

由式（23）可知，侧压力系数K并不是一个定值，而是与破坏面和水平面的夹角[θ]以及土的内摩擦角[φ]相关的变量。当挡土墙深度为60 m时，可得土侧压力系数K随[θ]和[φ]的变化关系，如图4所示。当[θ]为定值时，土侧压力系数K随填土有效内摩擦角[φ]的增大而减小;当[φ]为定值时，侧压力系数K随[θ]增加而先增大后减小，且在[θ]=50°时达到峰值。

4 槽壁局部失稳判据及参数敏感性分析

根据前文分析，槽壁稳定的条件是泥浆有效护壁压力对矩心O的力矩不小于主动土压力Px对矩心O的矩。由于有效护壁压力与主动土压力均作用于泥膜，以有效护壁压力与主动土压力的平衡关系作为槽壁局部失稳的判据，槽壁稳定富余压力[P富余]为有效护壁压力式（4）与主动土压力式（24）之差。

[P富余=P有效-Px]                      （25）

由式（25），可根据土体参数、泥浆参数、施工情况作出护壁富余压力沿槽壁深度的分布关系。当富余有效压力小于零时，则可能发生局部失稳。

以开挖速率V（取值范围1～4 m/h）、泥浆粘度s（取值范围18～35 s）、土层等效内摩擦角φ（取值范围18°～28°）、土层重度γ（取值范围1.05～1.25 kN/m3）、开挖深度H（取值范围20～60 m）为参数，且各参数在取值范围内按0～1范围标准化，根据式（25）分别取不同参数组合计算富余有效护壁压力，并拟合，可得：

[P富余=0.066s-0.1V+0.067φ+0.026γ-0.04H] （26）

其中，[V]，[s]，[φ]，[γ]，[H]分别为以上参数的标准值，标准化计算公式如下：

[A=A-AminAmax-Amin]                       （27）

由式（26）可以看出，影響富余有效护壁压力的因素敏感性排序分别为：开挖速率>等效内摩擦角>泥浆黏度>开挖深度>泥浆重度。

因此，在控制槽壁稳定性过程中，最重要的是控制开下切速率，其次是根据土层等效内摩擦角采取合理的加固措施，最后是泥浆黏度及重度的合理配制。

5 工程应用

5.1 工程条件

建新南路站位于福州市仓山区百花洲路南侧，为地下3层岛式车站，车站内净总长151.8 m，站中心基坑深度约24.15 m，顶板覆土约3.49 m。主体围护结构均采用 1 000 mm地下连续墙，共有64幅，连续墙顶标高5.3 m，底标高-54.3 m，墙高59.6 m。建新南路站地连墙施工时，采用传统的三抓成槽一次到底的施工方法。

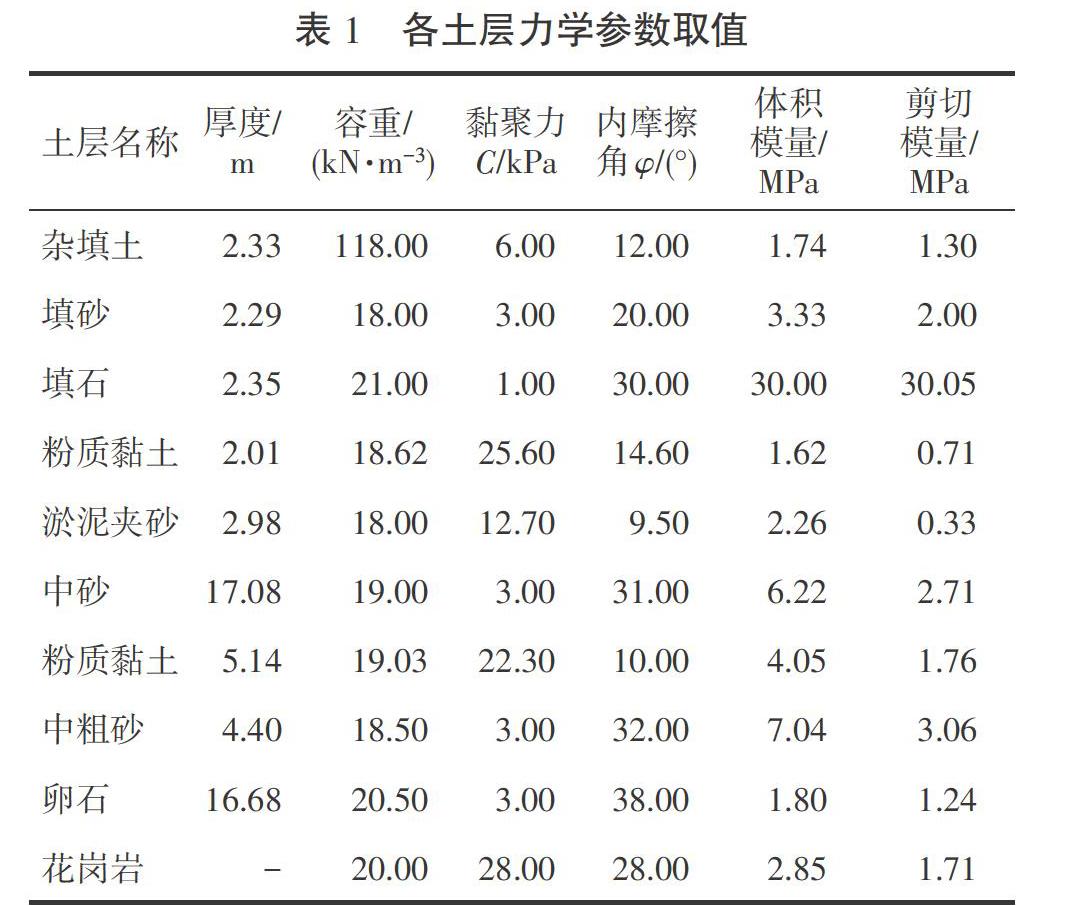
主要地层分布为：①杂填土。以人工堆填的黏性土为主，夹杂有碎石、砖块等建筑垃圾，局部含少量中粗砂和淤泥。②填砂。以砾粗砂、中粗砂回填为主，局部夹有少量填石和黏性土，层顶埋深1m，层底埋深6.8 m。③填石。以碎石块为主，粒径一般为5～35 cm，最大粒径>130 cm，填石含量约60%～90%，层顶埋深0～0.5 m，层底埋深1～5.7 m。④粉质黏土。局部夹少量碎石，层顶埋深1.8～3.3 m，层底埋深2.7～4.5 m，厚0.2～2.3 m。⑤淤泥夹砂。以黏粒为主，部分夹少量薄层细砂或混有少量砂，厚2.8～16.0 m。⑥（泥质）中细砂。以粉砂和中砂为主，均含有少量淤泥，级配较差，厚0.7～13.4 m。⑦粉质黏土。黏性较好，部分粉粒含量较高，土质不均，局部含少量砂。层厚1.4～6.4 m。⑧（含泥）中粗砂。粒径不均匀，上部以中粗砂、砾粗砂为主，局部夹有粉细砂透镜体及混有少量的淤泥，下部多含砾石、圆砾，厚2.1～20.1 m。⑨卵石。中密为主，饱和，卵石多呈椭球状，磨圆度较好，中等风化，粒径一般为3～20 cm，最大粒径>50 cm，含量为55%～85%。该层上部黏性土和砾石含量较高，下部主要为卵石，间隙主要由中粗砂充填，厚14.6～24 m。⑩强风化花岗岩（砂土状）。风化强烈，岩石坚硬程度属极软岩，岩体完整程度属破碎，岩体基本质量等级分类属Ⅴ类。层顶埋深55.6～59.5 m，层底埋深60.34～65.03 m，厚3.1～6.13 m，平均厚度4.42 m。

初见水位埋深为0.90～3.90 m，稳定水位埋深为1.50～4.70 m。主要含水层为第⑧⑨地层，现场钻孔提水试验表明砂卵石层为强透水层。各土层参数取值如表1所示。

5.2 应用效果

基于上述研究成果，根据开挖深度H及对应的土体等效内摩擦角、重度、以及实测泥浆黏度，代入式（26），选取合适的开挖下切控制速率。当降低下切速率不能满足局部稳定性控制要求时，采用投入锯末等措施增大局部土层等效内摩擦角的方法。通过验算分析，最终确定的泥浆性能指标为：比重1.05～1.08 g/cm3，粘度25～30 s，砂-黏土地层V=1 m/h，其他地层V=3 m/h，含沙率<4%，pH值8～9。验算的槽壁富余护壁压力分布如图5所示。

施工结束后的墙体声波检测结果表明：64幅连续墙垂直度及平整度均满足要求，合格率100%。

6 结 论

根据泥浆成膜机制，研究了有效护壁压力沿槽壁深度的分布形态。针对槽壁局部旋转破坏模式，给出了泥浆护壁作用下的槽壁主动土压力解析式。基于有效护壁压力与槽壁主动土压力的平衡关系，提出了以富余有效护壁压力判断槽壁局部稳定性的方法。研究发现：

（1）在地表以下10 m范围内及孔底以上5 m范围内槽壁上的泥浆有效护壁压力不足，是地下连续墙整体破坏及局部破坏的主要原因。

（2）富余有效护壁压力的影响因素按敏感性大小排序依次为：开挖速率>等效内摩擦角>泥浆黏度>开挖深度>泥浆重度。因此，选择合适的开挖下切速率对控制砂性土层的槽壁局部稳定性最重要，其次为改善土层等效内摩擦角。

（3）采用富余有效护壁压力判据，可以判断开挖面附近槽壁局部稳定性，并针对稳定性不足条件，方便地给出处理措施或施工控制指标。

綜上所述，富余有效护壁压力判据可有效解决地连墙槽壁稳定性判断问题。

参考文献：

[1] Washbourne J. Three-dimensional stability analysis of diaphragm wall excavations[J]. Ground Engineering， 1984， 17（4）：24-26， 28.

[2] 季冲平， 余绍锋. 地下连续墙泥浆槽稳定性分析的一种方法[J].华东交通大学学报，1998，15（3）： 13-17.

[3] 张厚美，夏明耀.地下连续墙泥浆槽壁稳定的三维分析[J].土木工程学报，2000，33（1）：73-76.

[4] Wong， Greg C Y . Stability analysis of slurry trenches[J]. Journal of Geotechnical Engineering， 1984， 110（11）：1577-1590.

[5] Hajnal I， Márton J， Regele Z. Construction of diaphragm walls[J]. Simon A B， Trans. New York： John Wiley & Sons Inc.，1984（48）： 1-6.

[6] 刘国彬，黄院雄.超载时地下连续墙的槽壁稳定分析与实践[J].同济大学学报：自然科学版，2000，28（3）：267-271.

[7] 姜朋明，胡中雄.地下连续墙槽壁稳定性时空效应分析[J].岩土工程学报，1999，21（3）：338-342.

[8] 李建军，邵生俊，杨扶银，等.防渗墙粗粒土槽孔泥皮的抗渗性试验研究[J].岩土力学，2012，33（4）：1087-1093.

[9] 杨春鸣，邵生俊.粗粒土地层防渗墙泥皮的形成机制及其抗渗性能试验研究[J].水力发电学报，2013，32（6）：208-215.

[10] 叶伟涛， 王靖禹， 付龙龙， 等. 福州中粗砂地层泥水盾构泥浆成膜特性试验研究[J]. 岩石力学与工程学报，2018，37（5）：1260-1269.

[11] 靳利安， 郭运华. 泥浆护壁压力分布形态及槽壁稳定控制方法研究[J]. 水利水电快报，2019，40（9）： 41-47.

[12] 丁勇春，李光辉，程泽坤，等. 地下连续墙成槽施工槽壁稳定机制分析[J]. 岩土力学与工程学报，2013，32 （增I）： 2704-2709.

[13] 王元战，李新国，陈楠楠.挡土墙主动土压力分布与侧压力系数[J].岩土力学，2005，26（7）：1019-1022.

[14] 应宏伟，蒋波，谢康和.考虑土拱效应的挡土墙主动土压力分布[J].岩土工程学报，2007，29（5）：717-722.

[15] 王仕传，凌建明.刚性挡土墙非线性主动土压力分析[J].地下空间与工程学报，2006（2）：242-244.

[16] 曹振民.挡土墙填土曲线破裂面主动土压力分析[J].中国公路学报，1995（增1）：7-14.

[17] 周旋.等效内摩擦角计算方法及其应用[J].水运工程，2016（7）：22-25.

（编辑：唐湘茜）

A new stability criterion of trench wall in constructing superdeep diaphragm wall

LI Zhiwen1，WEI Gang1，GUO Yunhua2，LI Yiyang2

（1. PowerChina Railway Construction Co.， Ltd，Beijing 100044， China ;   2. Hubei Key Laboratory of Roadway，Bridge and Structure

Engineering，Wuhan University of Technology，Wuhan  430070，China;  3. Wuhan University of Technology Advanced Technology

Research Institute of Zhongshan City，Zhongshan 528400， China ）

Abstract：As the trench excavation process is a continuous undercutting process， the stability control of trench wall still depends on the experience of engineering practice ， and the criterion of trench wall stability has not been finally resolved theoretically， stability accidents happen frequently. In this paper， based on the test results of slurry infiltration and film formation， using the principle of earth pressure balance on both sides of the slurry film， considering the rotating failure mode of the trench wall earth， the spatial distribution of the excess protective wall pressure along the trench depth is studied and the result shows that： the main factors affecting the stability of the trench wall are the equivalent internal friction angle of the earth， followed by excavation depth and excavation speed， and then the viscosity and gravity of the slurry. A new stability criterion of trench wall is set up based on the main affecting factors. The application of the study results in 60 m depth diaphragm wall at Xinjiannanlu of No. 5 subway in Fuzhou city， Fujian Province， showed that the analyzed weak stability area is located within 10 m below the surface and 3 m distance from the excavation surface， which is in accordance with the practical site condition.The stability criterion of groove wall based on surplus wall pressure can guide construction conveniently.

Key words：diaphragm wall; stability of trench wall; stability criterion; slurry trench wall protection; rotating failure