物理化学中热力学公式的学与用

＊任志博 刘晶 任冬梅 夏云生

（渤海大学 化学与材料工程学院 辽宁 121013）

引言

物理化学是化学学科的一个重要的分支，它采用物理学的基本理论和方法探讨化学变化过程中共同的基本规律，逻辑推理十分严谨，概念抽象，公式、定律较多，初学者常常感到困惑[1-2]。美国著名物理化学家莱文（I.N.Levine）曾说：“如果试图只通过阅读教科书而不做习题的办法来学习物理化学，其效果就如同为了改善体质却试图只通过阅读一本保养身体的书而不做所建议的体育锻炼一样。”要掌握这门科学，不通过解答习题的训练是不妥的[3]。做习题无疑是学习物理化学的重要的环节，是一种带有创造性的脑力劳动，通过解题可以加深对基本原理、基本概念和基本公式的理解，加强所学的理论知识，培养和提高分析问题和解决问题的能力。

物理化学课程中热力学部分，公式、符号和参量、参数非常多，而解答相关的推理题和证明题却要用到这些公式。除了循环关系、倒数关系、微分方程和链式关系外，常用的证明题解题方法有Bridgeman法、Jacobi行列式法、Tobolsky法等[4]。逐一牢记这么多公式是有一定的难度，而在应用相关公式时，能根据具体情况和使用环境及时顺利推出公式就可以了。

1.热力学公式的巧记

将物理化学课程中热力学部分常用的热力学状态函数和参数H、U、G、F、T、P、S和V标示于图1所示的位置上。温度T、压力P和体积V都是实验可测量，热力学能U和熵S具有明确的物理意义，而焓H、吉布斯能G和亥姆霍兹自由能F（有的教材使用A表示）是衍生出来的物理量。状态函数之间不是彼此独立的，除了基本定义式外，状态函数及其微分函数之间有12个基本函数关系，包括四个热力学函数基本方程，四组Maxwell关系式和四组特征偏微商关系式[1,2,5,6]。

图1 热力学函数的坐标记忆法Fig.1 The coordinate memory method of thermodynamic function

(1)热力学函数基本方程的巧记

热力学函数基本方程共有4个，即：

热力学函数基本方程，即某函数的微分等于相邻函数的微分与其各自同一直线上函数（箭头位置符号为正，箭尾位置符号为负）乘积的和。例如：对于函数G的偏微分dG等于其相邻函数T和P的微分dT、dP与其各自同一直线上函数S（箭尾位置符号为负）和V（箭头位置符号为正）乘积的和，则有dG=-SdT+VdP。

如果H、U、G、F用作自发性判据时，其对应的相邻函数不变，即图1（A）中位于同一个象限内的函数。例如对于函数U作判据时要求函数S和V不变，即ΔUS,V≦0。同样ΔHS,P≦0、ΔGT,P≦0和ΔFT,V≦0。

(2)特征偏微商关系式的巧记

从热力学函数基本方程可以导出很多重要的关系式，其中特征偏微商是重要的导出公式。以某函数（H、U、G、F）对任一相邻函数求偏导，另一函数恒定，等于与前函数在同一轴线上函数，符号依轴线位置确定，即箭头位置为正反之为负。例对于函数H对其任一相邻函数（S或P）求偏导另一函数不变，即，等于与S或P在同一轴线上的函数T或V，T和V在轴线的箭头位置符号均为正，即和。同理可以得到四组特征偏微商关系式，即：

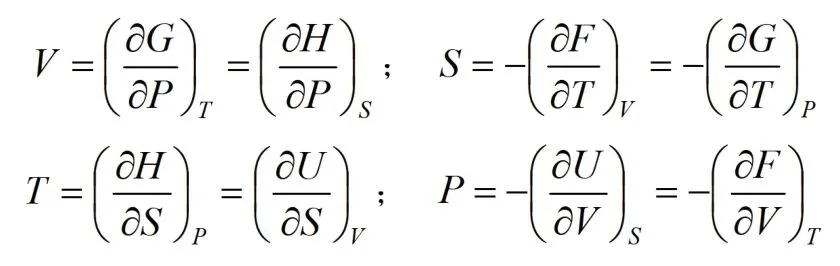
(3)Maxwell关系式的巧记

Maxwell关系式共有4组，以图1（A）中虚线框为记忆对象，以任意两个顶点为出发点划直角框如图1（B）所示，位于同一个直角线框上的微分数值相等，即的数值相等，其符号由微分式中分子函数S和P在图1中的位置确定，箭头指向方向为正，反之为负。S和P皆为箭头背向即皆为负，即。同理可以得出，。

2.应用举例

(1)证明某物理量的计算公式

热力学方法是靠热力学函数来回答热力学提出的问题，热力学函数之间的大量关系式的应用有助于理解和运用热力学方法与理论，总的思路是利用热力学定律、定义和转换方程，将不可测量的量转化为可以测量的量，或者向着题中要求的方向逐步推进，直到最终结果。具体的转化方法视不同的要求而定。

例1：证明封闭体系内理想气体的等温可逆膨胀过程中，体系与环境交换的热量是。

解：根据热力学第一定律，一个过程的热量Q等于过程的热力学能的改变量ΔU扣除过程中的功W，即，理想气体的热力学能只是温度的函数，理想气体的等温过程ΔU=0。

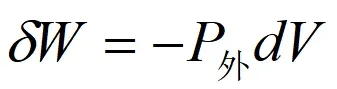
(2)证明理想气体某些性质与其他性质无关

这里主要是证明理想气体的热力学能U、焓H以及CV、CP都与压力P和体积V无关。

例2：对于理想气体，证明CV与体积V无关。

(3)证明U，H与CP，CV及T，V，P的关系

对于均相体系来说，热力学量H，U，T，V，P中只要有二个是独立的，五个量之间必然存在着确定的关系。T，V，P都是实验可测量的量，而实验上不能测定H和U的绝对值，但H，U随T，V，P的改变量可以用可测量的量表示。

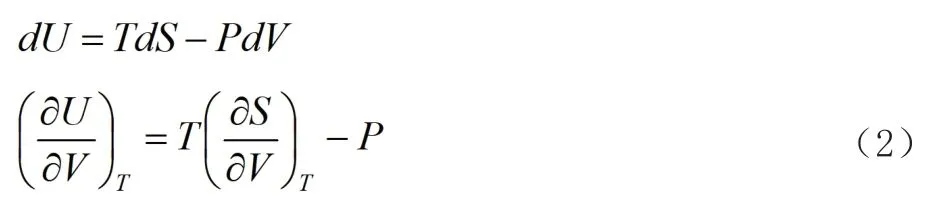
将（2）代入（1）有：

(4)Tobolsky方法求解

Tobolsky方法的基本思路是先将偏微分商分子和分母的全微分按各自的特征变量展开，再将式中不易测量的全微分进一步化成易测量的变量的函数而展开，用变量全微分的系数相等关系列方程组，求解即可。

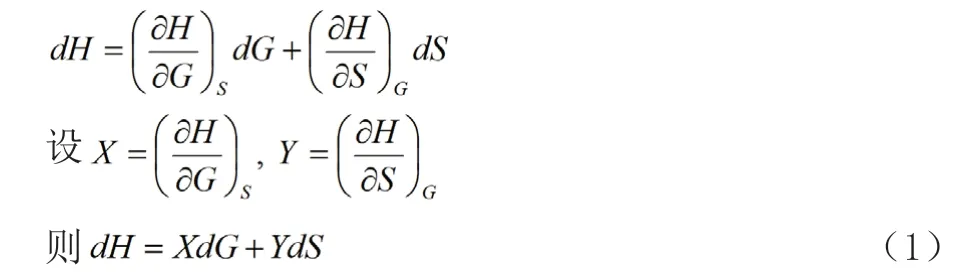
代入（1）式可得：

将上述结果全部代入（2）式，得：

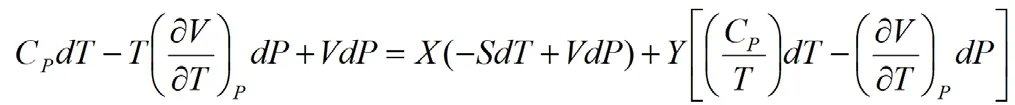
等式两边整理后，分别使dT和dP的系数相等，列出方程组：

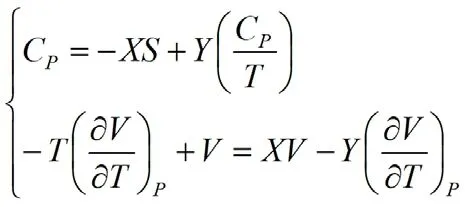
解方程组可得：

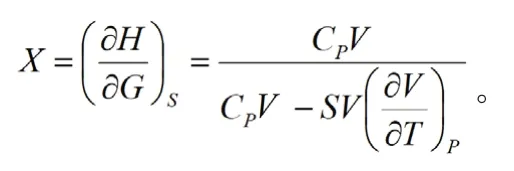
3.结束语

物理化学中公式较多，一一记牢是很难的，在应用时，能根据具体情况顺利地推导出公式就可以了。证明这类题，一是要真正理解所涉及的各个概念的含义，二是要对所涉及的基本定律、基本原理要熟悉。通过化学热力学公式的教学研究，在教与学过程中采用坐标法巧学巧记巧用化学热力学公式，对于初学者是行之有效的方法。通过学习和实践加深了对公式及使用条件及使用环境的理解，印象深刻。对其他学科和其他教学内容的教与学业有一定的参考价值。